电动汽车入网控制策略研究综述
冯培磊 董治全 徐天奇 李 琰 刘晓欣
(1. 云南民族大学电气信息工程学院,昆明 650500;2. 云南电网有限责任公司怒江供电局,云南 怒江 673100)
电动汽车入网控制策略研究综述
冯培磊1董治全1徐天奇1李 琰1刘晓欣2
(1. 云南民族大学电气信息工程学院,昆明 650500;2. 云南电网有限责任公司怒江供电局,云南 怒江 673100)
随着电动汽车大规模普及,电动汽车入网在时空上的不确定性问题将会凸显。针对国内电动汽车发展现状,采用控制策略使大量电动汽车有序接入电网成为现在研究的热点,大量研究表明电动汽车有序入网要比无序入网给电力系统带来的影响要小很多。本文通过对电动汽车接入电网控制策略进行对比分析总结,提出了控制策略中的不足并进一步进行深入分析,为后续电动汽车入网控制策略提供了可靠性参考意见。
电动汽车;入网;控制策略
传统汽车尾气的排放给空气带来影响,各国政府在新技术开发方面高度重视。电动汽车(Electric Vehicle)将清洁电能转化为汽车的动能,在人们长期的使用过程中可以实现碳的零排放[1]。中国人口基数大城市化进程加快为 EV的推广提供了契机。虽然接入电力系统可以有效降低CO2的排放总量[2],可是目前面临很多技术瓶颈问题[3]。无线充电技术[4-5]和智能充电服务网络[6]将成为智能电网发展的重点和难点。
充电站运营商通过对EV荷电状态信息采集[7],在满足客户需求和配电变压器不过负荷条件下最大程度达到削峰填谷的效果。对峰谷电价的定价措施使 EV合理充电,达到电网、运营商和客户共赢的目的。通过对 EV有序接入和无序接入电网的结果分析动态实时的响应分时电价,可以明显提高电动汽车充电站的盈利水平[8]。采用分时电价的同时可能会引发新的问题,夜间 EV充电的电价比较低,大规模的 EV同时有序接入的充电桩,可能引起用电高峰出现并且减小配电变压器的使用年限。通过建立了EV用户响应和校正下的峰谷分时电价模型[9],在不同的地区针对峰谷电价的实施情况也不一样,应该结合当地的经济情况来去定价。
前期控制策略研究主要是集中式控制[10-13],EV接入微电网充分利用清洁能源,可以提高微电网环境和经济效益[14]。分层分区调度策略控制优势相对明显[15]。以实时电价为背景实现用户侧与供电侧的双赢[16],对于特定车型在满荷电状态条件下,最大的行驶里程也是固定的。采用马尔科夫链型与Dijkstra算法量化EV充电需求点时空分布情况[17]。提出充电控制策略方案的在线应用[18],通过控制器控制住宅区负荷值小于设定功率限值,在满足 EV充电条件下最大程度利用低谷时段充电。分层控制的方案简单易于扩展,对大量 EV入网控制比较实用[19-20]。为解决 EV无序入网充电引发的“峰上加峰”的问题,合理的调动 EV用户有序充电是有必要的[21]。EV入网会对系统整体规划、运行方式和充放电的利用与控制等方面进行论证[22]。当前关于V2G的控制策略理论研究中发现EV用户对调度模式的响应度比较低,很难在市场上大规模的推广应用。深入分析放电优缺点[23],制定了放电价格的范围,并以京津唐电网的实际情况分析得出V2G模式的实施可以降低电网的日负荷方差使用户受益。EV可以在电网高峰时段作为电源对电网供电,在电网低谷时段作为负荷从电网获取电能,电动汽车参与电网的负荷调节具有一定的实际意义[24]。文献[25]以快速充电站为背景,通过制定峰谷、峰平、谷平时段的充电价格,用户根据 EV的荷电状态合理的选择充电起始时间减小充电成本。根据公交车的运行规律将快速充电成本最低为目标[26],通过对入网时间有效控制减小负荷波动带来的影响。通过对上层模型节点阻塞电价的求解去优化下层的 EV充电负荷[27],上下双层互联可以提高电网和用户之间的双向通信有利于EV的调度。EV入网控制策略就是要通过一些措施或者方案使电动汽车有序接入电网,实现电网波动最小、运营商与电动汽车用户获取经济利益最大化。
1 EV接入对电网产生的影响
文献[28]EV可以当做分布式电源的一种为电网提供反方向服务,同时可以减少基础设建设的投资提高电力系统的稳定性,EV每天的行驶时长接近3个小时,多数时间EV都处于闲置的状况。EV可以为基本负荷和高峰负荷段时间提供电能。大规模的EV可以作为移动备用电源灵活使用。当一定数量的EV作为负荷接入会对系统配电网络产生影响,会改变接入点的日负荷曲线降低峰谷差达到削峰填谷的作用。特别是 EV夜间大规模入网使配电网功率增大,需要重新考虑需求侧的管理。文献[29]EV作为新增负荷在一定程度上改变配电网结构,充电行为的不确定性会对系统稳定和效益带来严重的影响。如果不能合理的控制充电负荷,就可能引起短时间内负荷上升。文献[22]充电负荷具有很大的随机性,增加了配电网规划的复杂程度。对配电网产生的影响如图1所示。
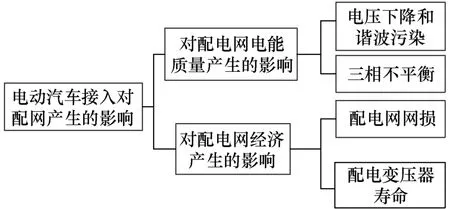
图1 EV接入对配电网产生的影响
2 EV入网影响因素数学模型
文献[30]将一天中 EV的第一次出行时刻和最后一次出行结束时刻近似表示为正态分布函数,每天行驶路程近似为对数正态分布函数密度函数,具体结果如下。
第一次出行开始时刻的正态分布函数为

式中,us=8.92;σs=3.24。
最后一次出行完成时刻对数正态分布函数为

式中,ue=17.47;σs=3.41。
文献[31]日行驶里程的概率密度函数为
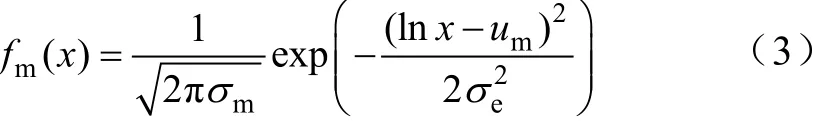
式中,um=2.98;σm=1.14。
通过对居民用户一天当中第一次出行时刻和最后一次出行结束时刻可以统计出 EV用户的出行规律。通过对相关数据进行分析运用数学模型进行函数拟合可以预测未来最近一段时间电动汽车的运行规律,对于充电站运营商来说可以合理的安排入网充电的时间点避免了大规模集中接入的情况。通过对日行驶里程的概率密度分析汽车荷电状态,充电站运营商根据充电功率合理安排电动车的充电时间。
3 充电价格的不同标准
3.1 EV充电定价模型原理
客户对价格有很小的可觉差范围。在很小的价格尺度内,用户基本没有反应。当超过最小差别阈值,用户对价格的响应呈线性关系。用户对价格的反应也有一个满足值,当大于这个恒定值客户对价格失去响应。要想使用户从高峰时段转移至低谷时段充电价格的调整应该在线性区的变化范围内刺激EV用户。文献[9]定义EV对价格变化下的积极性转移用分时电价措施执行后从充电价格较高时间段转移人数与原来人数的比值。峰谷模式下分时电价模型中横坐标为峰谷时段的电价差,纵坐标为峰谷时间段转移用户的百分比即用户的响应度。A、B分别表示死区拐点、饱和区拐点。峰谷模式下用户价格响应曲线如图2所示。

图2 峰谷模式下用户价格响应曲线
响应模型表达式为

式中,ΔCpv,1为死区阈值为充电峰谷时间段用户开始对峰谷充电价格差值有反应;ΔCpv,2表示饱和区阈值为充电的峰谷时段用户对峰谷电价差值不再有响应的;αpv,max为用户转移数量百分比的饱和值;kpv表示充电峰谷时间段价反应曲线的斜率。
3.2 电动汽车充电电价模型
1)基于节点阻塞电价的定价模型1
文献[27]通过拉格朗日乘子与功率传输分布因子求解节点的边际电价,将分时电价与变化的阻塞电价之和作为电动汽车用户的充电电价。
直流潮流条件下为获得利润最大:
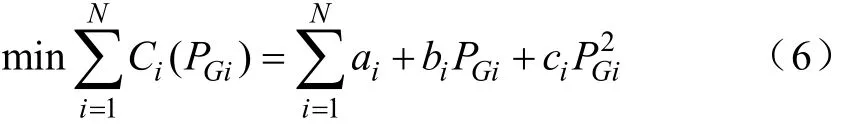
式中,Ci(PGi)为节点i机组的购电费用函数;ai、bi、ci分别为机组的购电费用系数。
直流最优潮流求解的拉格朗日表达式为

式中,Fk-i=ΔPk/ΔPi;ΔPk为支路 k功率变化量;ΔPi为节点i注入功率变化量为;M支路数目;δ 为均衡条件的拉格朗日乘子;PGi表示机组出力。
则节点边际电价为
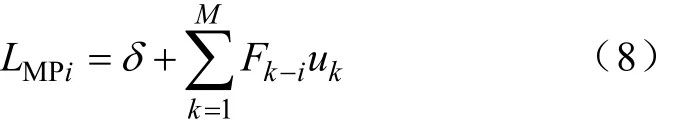
节点实时的阻塞电价为

即某一时刻的节点电价πi,t为

2)分时电价定价模型2
文献[25]提出分时充电价格的定价方法,可以引导汽车有序接入的同时减少运营商购电和用户充电费用。运营商购电成本最低获取计划充电负荷曲线,用实际充电负荷与目标计划负荷偏差值思考用户的反应度。引领后各时间段实际充电负荷与目标计划负荷方差值最小为目标,即
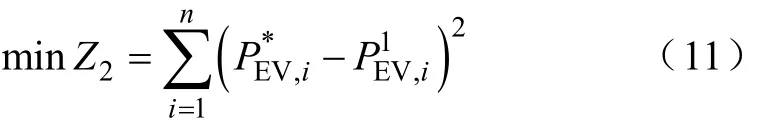
运营商向用户收取电网电费和服务费用。则引导后的运营商向EV用户收取的费用为
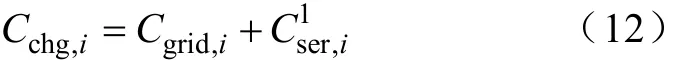
式中,Cchg,i运营商收取的总费用;Cgrid,i电网电费;运营商服务费用。
3)实时电价定价模型3
文献[32]电价和负荷需求关系可以分段线性化,第一部分为基本电价,第二部分为用户对负荷波动的响应电价,当季节变化对电价波动影响比较小,文献[33]电价与负荷的关系为
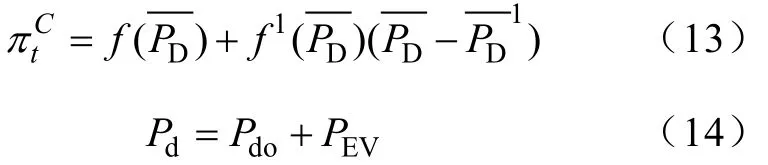
3.3 定价模型综合评价
电价的定价方式可以通过对用户的消费产生刺激实现负荷的跨时空转移,从而实现电力系统稳定。不同的定价方式与EV的区域性行驶规律有关。
定价模型1将分时电价与浮动阻塞电价之和作为充电电价可以动态的反应电价变化。当没有阻塞发生,充电电价即分时电价;当阻塞发生的条件下要将阻塞和分时电价考虑在内。节点阻塞电价模型能够在合适的范围内减少高峰时段的负荷,避免了线路潮流越限的情况,在一定程度上减少电网阻塞现象发生的概率。通过用户对节点阻塞电价一定程度的响应可减少充电费用获得收益。定价模型1与定价模型3都是在基本的分时电价基础上与负荷波动产生的电价的叠加和来去定价。模型2分时电价可以对充电行为进行指导,减少运营商从电网购电的成本。通过入网时间的调控可以让运营商的购电成本和用户的充电费用减少。充电负荷的峰谷差率减小有益于电网的稳定运行。提出的模型2仅仅适用于公司和居民区停车场等集中充电站的优化控制,相对于分散的小型充电站有待深入分析。相对于模型2来说,模型3实时电价在电网侧可以减少峰谷差在用户侧可以合理安排充放电计划,当 EV作为负荷充放电后会产生会产生新的充电电价可以体现出负荷变化与电价之间的关系。负荷与电价呈正相关,实时电价的实施让负荷跨时段转移。将电价曲线进行一阶泰勒公式展开可以使峰谷差减少并没有完全抑制电网负荷波动。运营商的选取应该符合地域的实际情况,否则产生很大误差。
4 EV控制策略分析
4.1 EV充电负荷模型
文献[34]EV作为新兴的负荷可以灵活调控:假设第k量EV的入网时间是,入网时用户的电池荷电为,用户预计时间是,并且要求离网 时刻电池SOC必须满足;电动汽车k的能量需求 E为

式中,为电动汽车 k的电池容量;Lk为电动汽车的充电效率。
EV的充电时间为

在分析EV充电时假设以平均功率充电:

模型存在的问题是上下边界值的问题,如果设置不恰当,就可能会出现电动汽车离开电网时,电池的充电需求没有达到用户期望值的情况。还应该设置一种应急机制,当充电用户临时有事需要离开时,用户没有按照提前设定的充电时间完成充电需要对充电费用在一定的范围内微调。
4.2 相关控制策略模型
1)策略一
文献[8]建立充电站有序充电的控制模型根据变压器的以往负荷数值预测当日 96点常规负荷曲线,时间间隔取值 15min。在配电变压器不超载和最大程度满足客户要求为条件,运营商获取最大利益建立目标函数,即

式中,cj充电站从电网的购电电价;pj运营商向用户收取的电价;j表示运营商协调控制的时间段数;Snj为从当前时间算起第 j个时段上充电机 i的泊车状况;Cnj为第n个充电机以当前时刻为起始点的第j个时间段的控制决策。
2)策略二
文献[2]将低碳的概念考虑在内,以机组发电成本和CO2排放量的收取费用和运行商补贴费用最低为目的。建立函数,即

式中,Cp为发电机能耗成本;Cc为CO2排放费用;CEV为服务补偿费用。
3)策略三
文献[1]首先优化目标为系统总负荷的削峰填谷:
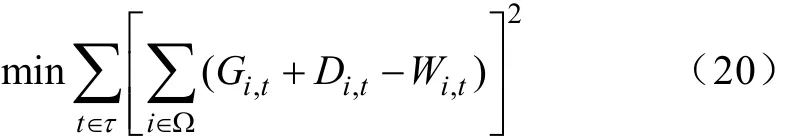
式中,Gi,t、Di,t和Wi,t分别为i级控制中心t时刻EV指导负荷、总常规负荷与新能源出力;Ω代表控制中心集合。
EV总负荷曲线与负荷指导曲线的欧式距离最小:

式中,Pt为t时刻EV总充电负荷,Gt为控制中心负荷指导曲线t时刻的分量。
4)策略四
文献[25]为了让运营商获利最大,最大程度转移到电价相对较低的低谷时段,建立目标函数为

式中,Z1为当日购电成本,n为EV一天内充电时间段总数取值为24;表示第i时段充电目标负荷;Δti表示第i时段充电时长;Cgrid,i表示第i时段分时电价。
以引导后各时段充电负荷与目标负荷方差最小,其函数表达式为

5)策略五
文献[21]同时将电网和用户的收益考虑在内,在 EV可向电网馈电条件下,选取电网负荷均方差与用户成本做为优化的目标函数。负荷均方差可以反应出电网是否稳定,一天分为 24个时段,每辆EV在任意时段的充放电功率为控制变量,即
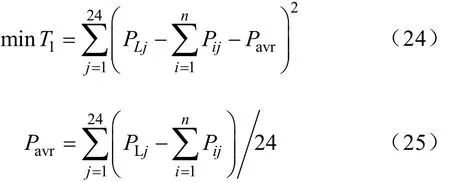
式中,PLj代表不含EV负荷的原电网j时间段功率;Pij代表电动汽车i在j时刻的功率;Pavr为调度后的日平均负荷;n表示电动汽车数量。
考虑分时电价下用户成本最低,即

式中,Sj代表电网在j时刻的电价。
6)策略六
文献[15]在上层模型中优化各运营商在不同时间段的调度规划,使系统在研究的时间内总负荷水平的方差最小,可以在一定程度实现削峰填谷。
上层目标函数包括两项:第一项为体系内总负荷的水平方差,第二项为基层各运营商实际调度情况与系统具体的调度规划情况偏差之和最小。优化目标函数,即

式中,T为动态调度周期中包含的时间段数;Pd,t为时间t除充放电负荷出力之外的其他负荷;为T个时段内的系统平均负荷;xk,t为代理商k在t时段的的调度计划;N0系统中所包含的代理商个数;θ 为惩罚系数;Xk为系统调度机构制定代理商k在各时段的调度计划;Yk为代理商k制定管辖EV每个时段的充放电策略;yk,1,t=1和 yk,1,t=-1分别表示其出状态为充电和放电;nk为代理商 k所管辖的电动汽车数量。
在下层模型中,各代理商通过对所属范围内的EV各时段充放电状态的控制,使代理商实际负荷与调度计划的偏差最小化。对于第k个代理商,其目标函数可表示为

式中,Pk,m,t为属于代理商k的第m辆电动汽车实际调度结果。
7)策略七
文献[7]设站内第 i(i=1,2,3,…,N)号充电机的额定功率为Pi,系统每15min更新状态。在15min内,对于接入的第i号充电机的汽车,其充电至状态需要的充电时间段数量为Ji。

式中,Δt为一个时间长度取15min;γ 为充电机的充电效率。
以15min为间隔的电网负荷LN,j(j=1,2,…,96);LN,1为零时刻的电网负荷。所有参加V2G的充电总负荷为LC,j(共96个点),放电总负荷为LD,j。
将电网公司负荷数值与汽车充放电负荷数值叠加:
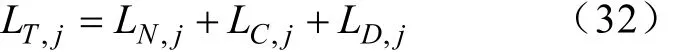
以电网总负荷方差值最小反映负荷的波动情况,建立函数如下:

式中,LN,i电网日负荷;LC,i电动汽车充电总负荷;LD,i放电总负荷;LN,j、LC,j、LD,j为对应的预测负荷。
4.3 综合评价分析
为了使 EV有序接入电网,针对于特定的实际情况中会采取不同的优化控制策略。EV将成为智能电网发展的重点。控制策略按照控制目标来分可以分为单目标和多目标控制策略,对于 EV入网控制策略来说也就是研究电网公司、充电站运行商和用户之间的关系。优化目标主要有电网负荷波动的方差最小,充电站运营商受益最大和用户的充电成本最低。
控制策略一与控制策略七为单目标优化控制策略都是采用96点负荷曲线进行研究,控制策略一重点研究运营商获益最大的策略。存在的问题是采用不同的时间间隔应该依据实际负荷情况合理设置。时间间隔的确定要根据历史负荷数据进行预测。在夜间谷时段,电价相对于运营商来说较低,运营商为了追逐利益最大化,充电站集中大规模的汽车充电可能导致局部高峰现象的出现。在客户紧急需求的条件下,在很短时间限内为用户提供 EV提供很多电能,充电站内不能满足要求出现客户离开的情况。在求解优化时不存在解。在某些情况下,通过简单分时电价定价调节不能解决局部峰谷差现象。单目标优化控制策略虽然使其获益最大,并不能保证电网负荷波动的稳定,在某些情况下也不能满足用户需求。
控制策略二将低碳理念引入控制策略并且建立了一定的惩罚措施。在策略二中运营商作为电网与电动汽车的媒介,实现信息与电能互动。相对于传统负荷,EV具备储能特点可以在G2V和V2G两种形式下运行。在CDM(clean development mechanism)市场条件下,CO2排放量对于发电主体来说具有一定标准尺度。EV通过充电桩获取电能的同时增加了CO2排放量。EV替代传统耗油汽车将CO2从交通转移到电力行业。虽然减少了CO2的排放量可是增加了发电成本。
控制策略四、策略五和策略七都是以分时电价为依据,策略四以运营商购电成本最小确定目标负荷曲线,用引导后的实际充电负荷与目标负荷方差最小为目标作为电网是否稳定的判据。策略五针对电动汽车调度机构建立计及电网负荷波动及用户成本的多目标优化模型。两个目标函数相互影响,不同分时电价改变峰谷电价差值和负荷方差值不一样、用户的充电成本也不相同。在考虑用户成本条件下,如何合理的选择分时电价,使峰谷差值和负荷均方差值减小值的研究。权重因子体现了各目标函数所占比重,其选择将直接影响优化结果,调度策略下在高价差和高均值且含尖峰分时电价下对调峰显著,可是会带来客户投资成本的增加。想达到综合最优要将合理的定价机制与权重分配考虑在内。
策略三与策略六都采用了分层的控制方法,分层控制策略具有比较好的扩展性,因地制宜结合各种调控方案,实现下级中心负荷紧跟计划目标负荷协同上级中心的削峰填谷优化。实行 EV有序充电负荷跟随的方案作为下级中心控制策略嵌入分层策略中,该控制策略可以根据电动汽车运行的实际情况进行架构的扩展,也可以深入分析 EV反送电的分层控制策略。
5 结论
EV作为新兴负荷接入给电网稳定带来影响,EV有序接入电网充电对电网产生的影响相对比较小。电网公司的要求是电力系统的负荷波动最小,EV运营商的目的是购电成本最小,在国家政策的控制下通过充电价格制定获取一定的经济效益。根据经济学分析在充电价格变化范围内,大量研究表明有效的控制策略可以让电网公司、充电站运营商和EV用户共赢。在分析多目标优化控制时重点考虑权重分配问题。随着电动汽车数量的巨增,大量电池的回收利用和充电站的规划设计将成为下一步研究的热点。
[1] 占恺峤, 胡泽春, 宋永华, 等. 含新能源接入的电动汽车有序充电分层控制策略[J]. 电网技术, 2016,397(12): 3689-3695.
[2] 娄素华, 张立静, 吴耀武, 等. 低碳经济下电动汽车集群与电力系统间的协调优化运行[J]. 电工技术学报, 2017, 32(5): 176-183.
[3] 吴奇珂, 程帆, 陈昕儒. 电能替代"战略中电动汽车的推广潜力及经济性分析[J]. 电气技术, 2016, 17(9):88-92.
[4] 赵争鸣, 刘方, 陈凯楠. 电动汽车无线充电技术研究综述[J]. 电工技术学报, 2016, 31(20): 30-40.
[5] 郑心城, 陈为. 电动汽车无线充电的磁耦合结构综述[J]. 电气技术, 2017, 18(4): 15-92.
[6] 戴咏夏. 电动汽车动力电池运维精益化管理探索与实践[J]. 电气技术, 2016, 17(3): 120-122.
[7] 徐智威, 胡泽春, 宋永华, 等. 基于动态分时电价的电动汽车充电站有序充电策略[J]. 中国电机工程学报, 2014, 34(22): 3638-3646.
[8] 徐智威, 胡泽春, 宋永华, 等. 充电站内电动汽车有序充电策略[J]. 电力系统自动化, 2012, 36(11):38-43.
[9] 阮文骏, 王蓓蓓, 李扬, 等. 峰谷分时电价下的用户响应行为研究[J]. 电网技术, 2012(7): 86-93.
[10] 李秋硕, 肖湘宁, 郭静, 等. 电动汽车有序充电方法研究[J]. 电网技术, 2012, 36(12): 32-38.
[11] 孙波, 廖强强, 谢品杰, 等. 车电互联削峰填谷的经济成本效益分析[J]. 电网技术, 2012, 36(10): 30-34.
[12] 占恺峤, 宋永华, 胡泽春, 等. 以降损为目标的电动汽车有序充电优化[J]. 中国电机工程学报, 2012,32(31): 11-18.
[13] 宫鑫, 林涛, 苏秉华. 插电式混合电动汽车充电对配电网的影响[J]. 电网技术, 2012, 36(11): 30-35.
[14] 赵兴勇, 王帅, 吴新华, 等. 含分布式电源和电动汽车的微电网协调控制策略[J]. 电网技术, 2016,40(12): 3732-3740.
[15] 姚伟锋, 赵俊华, 文福拴, 等. 基于双层优化的电动汽车充放电调度策略[J]. 电力系统自动化, 2012,36(11): 30-37.
[16] 邹文, 吴福保, 刘志宏. 实时电价下插电式混合动力汽车智能集中充电策略[J]. 电力系统自动化,2011, 35(14): 62-67.
[17] 舒隽, 唐刚, 韩冰. 电动汽车充电站最优规划的两阶段方法[J]. 电工技术学报, 2017, 32(3): 10-17.
[18] 齐先军, 李冬伟, 纪姝彦. 采用功率限制的住宅区电动汽车有序充电控制策略[J]. 电网技术, 2016,40(12): 3715-3721.
[19] Xu Zhiwei, Su Wencong, Hu Zechun, et al. A hierarchical framework for coordinated charging of Plug-In electric vehicles in China[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 428-438.
[20] 唐佳, 高爽, 王丹, 等. 入网电动汽车集群的分层控制方法[J]. 电力建设, 2015, 36(7): 146-162.
[21] 魏大钧, 张承慧, 孙波, 等. 基于分时电价的电动汽车充放电多目标优化调度[J]. 电网技术, 2014,38(11): 2972-2977.
[22] 胡泽春, 宋永华, 徐智威, 等. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报, 2012, 32(4):1-10.
[23] 项顶, 宋永华, 胡泽春, 等. 电动汽车参与V2G的最优峰谷电价研究[J]. 中国电机工程学报, 2013(31):15-25.
[24] 李惠玲, 白晓民, 谭闻, 等. 电动汽车与分布式发电入网的协调控制研究[J]. 电网技术, 2013, 37(8):2108-2115.
[25] 常方宇, 黄梅, 张维戈. 分时充电价格下电动汽车有序充电引导策略[J]. 电网技术, 2016, 40(9):2609-2615.
[26] 李斌, 刘畅, 陈慧妙, 等. 基于混合整数规划的电动公交车快速充电站有序充电策略[J]. 电网技术,2016, 40(9): 2623-2629.
[27] 麻秀范, 王超, 洪潇, 等. 基于节点阻塞电价的电动汽车双层充电优化策略[J]. 电网技术, 2016, 40(12):3706-3714.
[28] 涂轶昀, 李灿, 承林, 等. 电动汽车接入电网及其对电力系统的影响[J]. 华东电力, 2011(7): 1085-1088.[29] 赵俊华, 文福拴, 杨爱民, 等. 电动汽车对电力系统的影响及其调度与控制问题[J]. 电力系统自动化,2011, 35(14): 2-10, 29.
[30] 田立亭, 张明霞, 汪奂伶. 电动汽车对电网影响的评估和解决方案[J]. 中国电机工程学报, 2012,32(31): 43-49, 前插 6.
[31] 田立亭, 史双龙, 贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术, 2010, 324(11):126-130.
[32] 麻秀范, 王超, 洪潇, 等. 基于实时电价的电动汽车充放电优化策略和经济调度模型[J]. 电工技术学报,2016, 31(S1): 190-202.
[33] Kristoffersen T K, Capion K, Meibom P. Optimal charging of electric drive vehicles in a market environment[J]. Applied Energy, 2011, 88(5): 1940-1948.
[34] 孙强, 许方园, 唐佳, 等. 基于需求响应的电动汽车集群充电负荷建模及容量边界控制策略[J]. 电网技术, 2016, 40(9): 2638-2645.
Summarization of Strategy about Electric Vehicles Connected to Power Grid
Feng Peilei1Dong Zhiquan1Xu Tianqi1Li Yan1Liu Xiaoxin2
(1. School of Electrical and Information Technology, Yunnan Minzu University, Kunming 650500;2. Nujiang Grid Bureau, Yunnan Grid Corporation Limited, Nujiang, Yunnan 673100)
With the development of electric vehicle faster and faster, the uncertainty over time and space of vehicle-to-grid is the essential problem. The massive application of control strategy makes vehicle -to-grid charging orderly, which is a hot topic of the research. In view of the development of electric vehicles in China, numerous research demonstrates that ordinary access of vehicle-to-grid has less effect than the disorderly access. Based on the control strategy analysis summary of vehicle-to-grid,pointed out the shortcomings in control strategy of vehicle-to-grid, and made a further analysis, put forward reliable references to control strategies of vehicle-to-grid.
electric vehicle; schedule of EV charging; control strategy
国家自然科学基金项目(61461055)
云南电网公司怒江供电局职工技术创新项目(050000KK52150006)
冯培磊(1992-),男,硕士研究生,安徽蒙城人,研究方向为智能电网、新能源发电接入,电力系统分析。

