用基本的方程解答,自然更深刻
2018-01-03 01:41:56贵州省毕节市七星关区碧海中学551700
中学数学研究(江西) 2017年12期
贵州省毕节市七星关区碧海中学 (551700)
陈晓霞
用基本的方程解答,自然更深刻
贵州省毕节市七星关区碧海中学 (551700)
陈晓霞
由于在中学数学中,可解方程(不等式)都是一次,二次以及可化为一次,二次的,因此求次数不高(不超过二次),元不多的多元代数式(函数)值域(最值),或证明多元不等式(求得多元代数式的值域(最值)就得最佳多元不等式),都可用方程函数解决(文[1]、 [2]),虽然不及用由函数y=x2的值域[0,+∞)产生的不等式x2≥0及其衍生的均值不等式、柯西不等式等放缩精彩,但无技巧之痛,且本质而深刻.
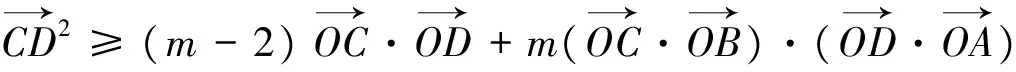

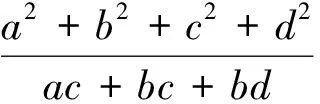

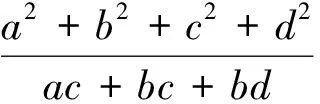
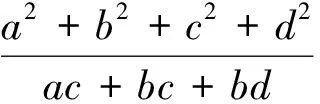
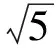
由解法3知,取得最小值的a,b,c,d不唯一,不用方程法是认识不到这一点的.
[1]熊福州,张龙跃.数学问题的根基本质是方程的解集[J].中学数学研究(江西),2015,8.
[2]熊福州.让技巧在换(消)元法中淡化[J].河北理科教学研究,2015,3.
猜你喜欢
中国乳品工业(2022年2期)2022-03-29 08:37:40
湘潮(上半月)(2019年11期)2019-05-22 06:09:52
当代贵州(2018年28期)2018-09-19 06:39:08
数学学习与研究(2016年18期)2017-01-07 12:12:59
初中生世界·七年级(2016年10期)2016-11-07 21:08:09
初中生世界·七年级(2016年10期)2016-11-07 21:05:59
音乐天地(音乐创作版)(2016年12期)2016-04-25 06:17:32
海关与经贸研究(2014年3期)2014-02-28 14:30:41
中学生数理化·八年级数学人教版(2008年6期)2008-09-05 03:46:12

