三角换元技巧与三元函数最值

江苏省泰州市苏陈中学 (225300)

房园园

三角换元技巧与三元函数最值

江苏省泰州市苏陈中学 (225300)

房园园

三角换元技巧是一种用三角函数代替问题中的字母，然后利用三角函数之间的关系而达到解题目的的一种代换方法，此法应用广泛，本文仅就这种方法在求解三元函数最值问题中的应用，精选部分高考数学题为例说明如下.

一、解最大值问题

分析:考题为三元二次方程限定下，求三元分式的最值问题，解决本题通常可运用换元思想，反用条件解题，但都较繁，然而根据条件，通过先配方，再利用三角换元技巧可简明求得其解.

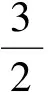
点评:本题考查的是三元函数最值的求法，它既是高中数学的难点内容，又是一道具有潜在价值的新颖题目.本题运用三角换元技巧求解，构思巧妙，别具一格，充分显现了三角换元技巧在解题中的重要作用，其解法简明流畅，令人赞叹.

二、解最小值问题

分析:本题所求的最小值是关于分式的三元函数，难度大，然而通过变换与变形便能透过现象看本质，找到了三角换元求解就简便了.

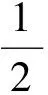
分析:本题为三元函数的最值问题，由于试题横向入口较宽，纵向难度较大，综合性和技巧性很强，因而学生感到很棘手.然而根据题设结构特征巧妙将已知条件变形，再运用三角换元技巧就可将三元函数转化为三角函数来求最小值，从而解题就便利了.

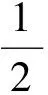
点评:上述方法是从条件入手，通过配方，将已知条件三角化后代入目标函数，实现了将代数最值问题转化为三角函数最值问题来处理.本题运用三角换元技巧法求解，不仅简洁明快，解法流畅，而且能启迪学生思维，提高解题速度，拓宽视野，符合新课程改革的理念，对于有效指导学生解题，激发学生的学习热情，均颇有益处.

三、解最大值和最小值问题

例4 (2015年苏锡常三市高考二模试题)若实数a，b，c满足a2+b2≤c≤1,求a+b+c的最大值和最小值.

分析:本题如从已知条件入手求解，则很难，但从结论入手通过设a=rcosθ,b=rsinθ,则可联系三角函数知识求得结果.此题设计精巧，根据题中条件的结构特征，利用三角换元思想解题可谓别具一格.

点评:本题属于三元条件最值问题，直接用代数方法解较难.然而根据已知条件式子的结构特征，联想三角换元，利用正弦函数有界性求得最大值和最小值.其解法思维自然，过程流畅，从而沟通了题设与结论之间的关系，使问题轻松得到解决.这种创新的思维流程，对于有效指导学生解题，激发学生的解题热情，提高学生的解题能力，大有裨益.

从以上各例可以看出用三角换元技巧求高考最值问题，其关键是要从问题的背景出发，根据题设所求题目的结构特征经过合理的推理，探究出问题中隐藏的三角函数关系，列出符合题意的关系式，从而与代数有关知识联系起来，以达到解题目的.

用三角换元技巧求解高考最值问题之所以具有新颖别致、独特创新的灵活性和创造性，是因为在解题过程中往往容易找到题设和结论之间的关系，使原来抽象隐含的条件充分显露出来，因而解题时，就能化繁为简，变难为易.

[1]于志洪.应用三角换元法解高考最值问题.[J].数学通讯(下期)，2014(1).

[2]于志洪.应用三角换元法解竞赛最值问题[J].数学通讯(上期)，2015(4).

[3]于志洪.代数法求最值十二曲[J].中学生理科应试.2013(4).

[4]于志洪，吴春胜.应用换元法解高考最值问题[J].中学生百科(高中学习).2013(3).