向量之三角形的“四心”

林海卫 叶 林

(浙江省温岭市技工学校 317500)

向量之三角形的“四心”

林海卫 叶 林

(浙江省温岭市技工学校 317500)

向量是既有大小，又有方向的量，具有双重性，是不能比较大小.平面向量的代数性质和几何特点非常明显，是连接几何和代数的工具，是数形结合的典范.平面向量的题目变化多端，可单独成题考查，也可结合不等式、三角函数、解析几何等知识考查.在学习时，我们要重概念，重基础，充分利用它的数形特征，体现向量的“工具性”.

向量；三角形；四心

三角形的“四心”与平面向量有着千丝万缕的关系，对这两者进行一定的探究，旨在探索题型规律，以提高学生的数学思维能力.以三角形的“四心”为出发点，利用向量的相关知识，巧妙地解决了三角形“四心”所具备的一些特定的性质.

一、向量之三角形的重心

三角形的重心是三条中线的交点(它到三角形顶点距离与该点到对边中点距离之比为2∶1).

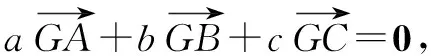
A．直角三角形 B．等腰三角形

C．等边三角形 D．钝角三角形

二、向量之三角形的垂心

三角形的垂心是三条高线的交点(它与顶点的连线垂直于对边).

A. 内心 B. 外心 C. 重心 D. 垂心

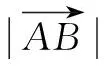
在△ABC中，由正弦定理可得：|AB|sinB=|AC|sinC，记|AB|sinB=|AC|sinC=k，则

三、向量之三角形的外心

三角心的外心是三条边的垂直平分线的交点(外心就是三角形外接圆的圆心，它到三角形的三个顶点的距离相等).

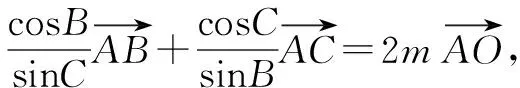
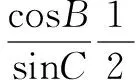
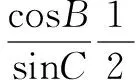
即cosBsinC+cosCsinB=m，从而m=sin(B+C)=sinA=sinθ.

四、向量之三角形的内心

三角形的内心是三个内角的平分线的交点(内心就是三角形内切圆的圆心，它到三角形三边的距离相等).

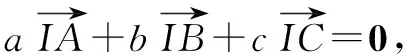
A. 内心 B. 外心 C. 重心 D. 垂心

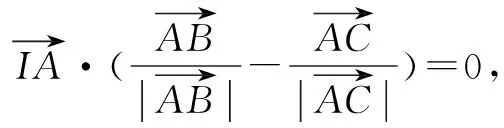
同理：IB是∠ABC的平分线，IC是∠ACB的平分线.故点I是△ABC的内心.

通过以上题型，笔者发现高中数学中以“向量为载体”对三角形的“四心”进行考查，是一道靓丽的风景线，需引起我们重视.

[1]连春兴.借“向量”之石，攻“几何”之玉[J].数学通报，2009(4)：14—16.

[2]彭燕伟. 高中数学新课标实验教材向量内容的比较研究[D].兰州：西北师范大学,2010.

G632

A

1008-0333(2017)31-0028-02

2017-07-01

林海卫(1983.10-)，男,浙江省台州人，本科,讲师,从事数学学科教学与研究.

叶林(1984.8-)， 女，浙江省台州人， 研究生， 讲师，从事数学教学与研究.

杨惠民]