对一道不等式试题的研究
贾彦龙
(甘肃省合水县第一中学 745400)
对一道不等式试题的研究
贾彦龙
(甘肃省合水县第一中学 745400)
本文对不等式恒成立问题,进行了多角度、多层次的分析与研究,渗透了数学中重要的两种思想方法——分类讨论的思想方法和数形结合的思想方法.
不等式;恒成立;分类讨论
近年来全国各地高考数学试题,考查不等式恒成立的有关试题非常普遍,这类问题既含参数又含变量,往往与函数、数列、方程、几何有机结合起来,具有形式灵活、思维性强、不同知识交汇等特点.
考题通常有两种设计方式:一是证明某个不等式恒成立,二是已知某个不等式恒成立,求其中的参数的取值范围.解决这类问题的方法关键是转化化归,通过等价转化可以把问题顺利解决.
例设f(x)=|a-3x|,g(x)=x-1.(1)若a=1时,f(x)+|g(x)|>4,求x的取值范围;(2)f(x)>g(x)对任意x∈[0,2]恒成立,求a的取值范围.

h(x)min=h(0)=1-a>0.∴a<1,∴a<0.
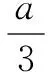
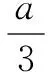
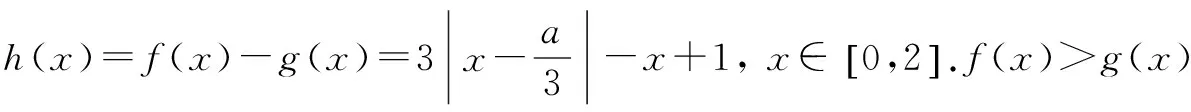

解法3f(x)>g(x)对任意x∈[0,2]恒成立



h(x)min=h(1)=3-a>0. ∴a<3.
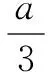
h(x)min=h(2)=a-7>0. ∴a>7.
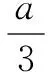

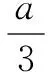
综上,a<3,或a>7.
解法4f(x)>g(x)对任意x∈[0,2]恒成立



总之,不等式恒成立问题,是教学中的难点,也是高考考查的重点内容之一.本文通过具体例题,对恒成立问题进行了多角度、多层次的分析与研究,体现了分类讨论的思想方法和数形结合的思想方法对解答数学问题的指导作用,对分析和研究高考同类试题有一定的启发.
[1]孟凡栋.恒成立型不等式中参数范围的几种求法[J].数学教学通讯,2004(01).
G632
A
1008-0333(2017)31-0019-01
2017-07-01
贾彦龙(1970-),男,汉,本科,甘肃省庆阳人,中学数学一级教师,重点研究高考数学解题的策略与思想方法.
杨惠民]

