交流电路时变电学特性探究
舒牧葳
(成都七中嘉祥外国语学校 四川 成都 610000)
交流电路时变电学特性探究
舒牧葳
(成都七中嘉祥外国语学校 四川 成都 610000)
在直流电路中,研究了电感和电容作为理想元件时,稳态电压电流的情形,在交流电路中,如果考虑到电感作为感性元件,其电流不能突然变化,而电容两端的电压也不能跃变,那么在电路开工作的初始态,将会表现出和一般直流电路完全不同的电学特性,并且最终电路将稳定工作在某一状态,本文将探究电路加电后随时间变化的电路特性,结合微分方程等数学工具进行解释。
交流电;跃变;初始态;电学特性;时变;微分方程
1 电路分析方法
欧姆定律给出了相对简单的电阻电路,结合基尔霍夫定律,可以应用这两种基本方法分析所有的电路,但是当电路结构更加复杂,设计更多的电路元件时,似乎我们的洞察力减弱了,使用直接的办法变得麻烦,首先回顾一下简单的电阻电路,其中我们使用分压法和分流法求解,然后又推导了电阻串联和并联的特性。从中可以注意到,流入任意一个电路节点的电流和流出该节点的电流相等,而任意两点之间连接的各支路之间的电势差也相等。
电压和电流也服从叠加原理,有了以上这些工具,在稳恒电流中不需要考虑电压电流的变化,这些工具已经够用了,进入到交流电路,电路回路中连接了电感电容,电路随时间的响应就不那么简单和直观,需要借助一定的数学工具进行分析。
2 电路元件电学特性及数学模型
电路中有电阻,电容、电感等常用元件,在理想状态下,稳态时电容与电感呈现了与电阻不同的非线性特性,而在电流电压瞬变时,电感会抵抗电流的变化,而电容会抵抗电压的变化。电感的端电压是与电感中电流随时间的变化率成比例的。用数学公式表示为:
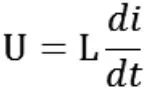
这个公式说明,电流稳定时,即当电流是常数时,理想电感两端的电压为0,其次,电感中的电流不能跃变,即电流在0时间内不能改变其大小。
电容则变现出于电感相异的特性,首先电容两端的电压不能跃变,电容的微分特性为:
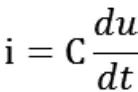
从上式可以看出,跃变对应的电流为无穷大,这在实际中是不可能发生的,其次,当电压维持不变时,电容的电流为0。
根据积分公式可知,对于电感有:
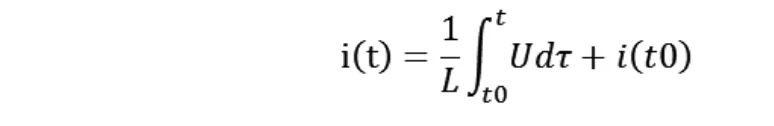
同样的对于电容有:
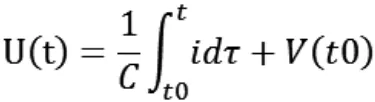
有了以上的基础,可以推论当电感串联时,通过电感的电流相同,但每个电感上的电压不同,而和电感量有关,总的电压是单个电感电压的总和,而当电感并联时,由于电感两端的电压都相等,电流则是电感电流之和,于是并联电感的等效电感量为:
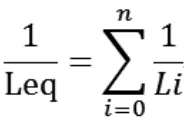
同理,电容串联的等效电容为:
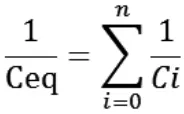
以上公式揭示了电感电容不同于纯电阻的电学特性,表明交流电路结合LC形成的回路,回路中的电流电压有较为丰富的相位关系,与稳恒电流的情况有较大的不同,以下主要采用微分方程这一数学工具,对电路特性进行探究。
3 RL电路及RC电路微分特性
考虑电路回路的多样性,有纯阻性元件和感性元件的回路,以及纯阻性元件和容性元件的回路,当电压源瞬间接通时,由于感性或者容性元件不能跃变的性质,在回路接通后,电感电容要阻碍原来的变化,电路的电特性和有一个快速变化的瞬态过程,并将最终趋向于稳定。探究电路启动后一段短暂的时间内的回路特性,有助于深刻理解电路实际工作的复杂性。以下按照RL电路,RC电路,RLC的电路逐渐深入。其中电源都考虑正弦交流电源。
4 RL电路数学模型
理想的正弦电压源与R、L串联,设理想电压源的电压特性为U=U0sinωt:
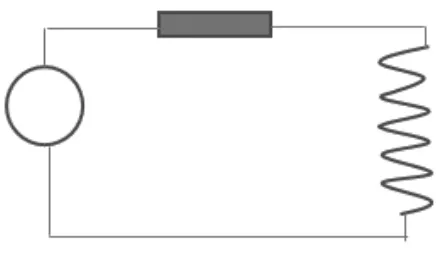
图1 RL电路理论模型
该回路接通后满足回路基尔霍夫定律:
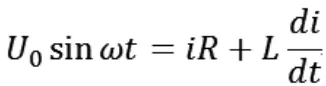
这是一阶微分方程,解之得∶

其中C为常数,该完全解给出了电流的数学表达式,可以看出电流是时间的函数,在任意时刻均成立,又在初始状态时,电流为0,于是:

代入得:
这个系数和R、ω、L均有关。

电流最终将趋向于稳态周期函数。电流的周期趋向于和电源的周期一致,相位上有一定的差别。
5 RC电路数学模型
理想的正弦电压源与R、C串联,设理想电压源的电压特性为U=U0sinωt,电容带电量为Q。
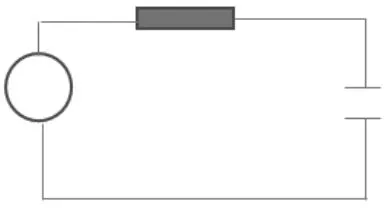
图2 RC电路理论模型
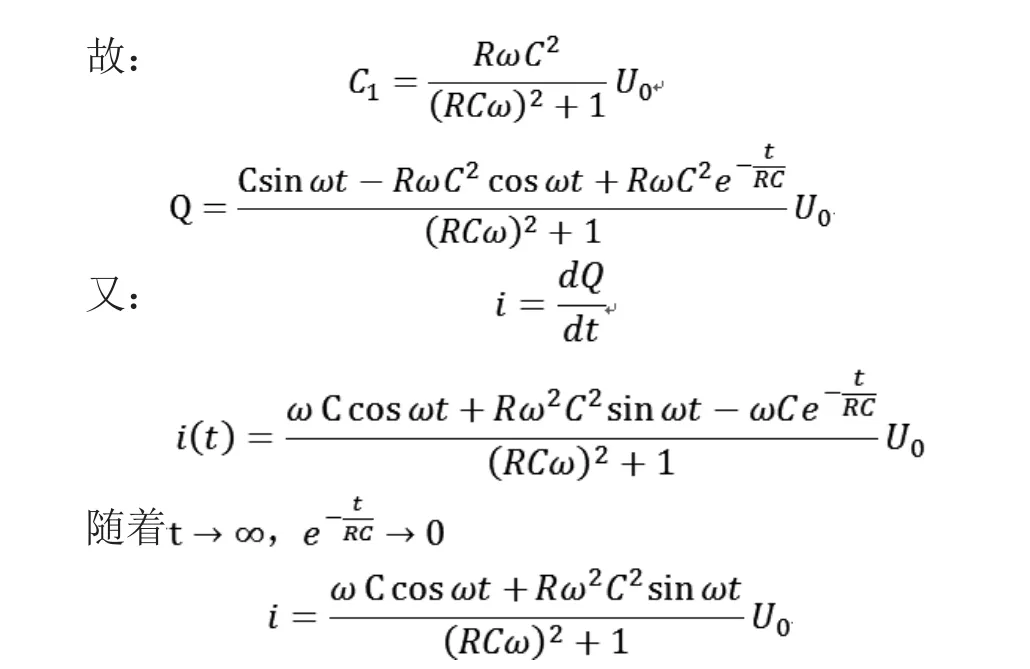
式中的第三项最终趋近于0,表明电路经过一段时间的振荡后,渐渐趋于稳定。此表达式为稳定时的电流。根据三角函数性质,该电流形式的周期和电源的周期一致,相位上有一定的差别。
RC电路的解的形式和RL是类似的,都包含了三项,三项一起称为电路的完全解,前两项是周期函数,属于一种稳定的震荡,第三项从数学形式上接近,但常数不同,分别是L/R与RC,这个常数称之为时间常数。
时间常数反应了这个暂态响应的时间长度。即电流或者电压趋于0的速度。这个速率的倒数就是电路的时间常数,对于一阶电路,是电流减到其初始值的e-1倍的时间。对于不同分R、L、C的取值,电路的时间常数的数值都不相同,即每个不同的实际电路,它从回路接通后开始看暂态过程,从开始振荡到逐渐趋于稳定的趋势虽然性质相仿,但从时间轴上看,有的相对快一些,有的要相对缓慢。
6 RLC电路数学模型
以下考虑最为复杂的一种电路,LC并联回路,连接关系如图3所示。
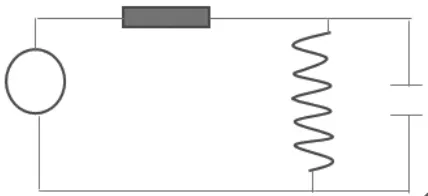
图3 RLC电路理论模型
该回路接通后满足回路基尔霍夫定律:

解上微分方程得:其中C1为常数,为了与RL电路中的常数C区分。该完全解给出了电流的数学表达式,可以看出电流是时间的函数,在任意时刻均成立,初始状态时,t=0,Q=0,
理想的正弦电压源与R串联、与L、C并联,设流经RL上的电流为I,流经L上的电流为iL,流经C上的电流为iC,根据电流的分流原则有:
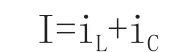
按照前文中关于电感电容的数学模型可知:
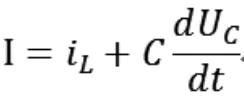
由于电感电容上的电压相等,于是存在以下关系:

将上述方程联立即:
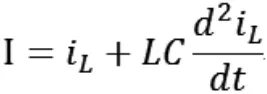
这是一个二阶的微分方程,直接求解该二阶微分方程比较复杂,表明其暂态过程非常复杂,为简化模型,本文只考虑稳定时的情形。
因为LC并联,所以LC上分得的电压相等,且相位相同,又因为R与LC串联,因此流过R上的电流等于流过LC上的电流之和。以下根据电感上的电压超前电流π/2相位,电容上的电压落后电流π/2相位。通过相位关系可以画出形如图4的矢量关系图,类似于力的合成,本文采用矢量合成方法求解。

图4 电压电流矢量关系图
根据电路模型,对应图中:

所以相位关系为:
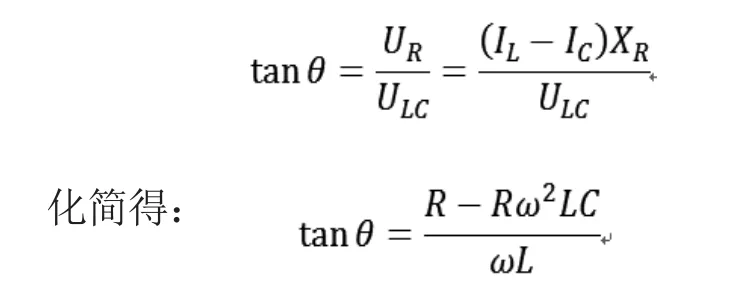
当电源电压为正弦电压U0sinωt时,可解得:

二阶微分方程的复杂程度超过了本文的讨论范围,故本文的求解没有直接用数学方法去解,当我们注意到了电感和电容电流和电压的相位超前之后,利用相位之间的确定关系,用几何法,只需要经过简单的计算,就可以了解到该电路的工作具体初始状态,该方法跳出了纯粹的复杂的数学运算,比较清晰的揭示了RLC电路中电流电压的相互关系。给出了解决LC并联电路的一种新方法。
从以上三个部分的讨论可见,当交流电压源突然作用时,电路中会有一段对抗变化的过程,这个过程的最终结果是在相对大幅的振荡后逐渐趋于稳定,类似于直流电压源的情形,交流电压源电路中,分析方法是相同的,考虑到电压源的周期性,趋于稳态后的电路响应,也有数学形式上的相似性,在存在一定相位差的前提下,正弦的电压源激发了正弦的响应,即源的性质决定了元件响应的性质,暂态过程有类似的形式,和具体的电路形式关联度相对较小。
7 结语
本文从电感电容的电路理论模型出发,先引用了其微分特性,给出了其数学的微分方程,然后分层次,从RL电路,再到RC电路,最后研究了RLC电路,给出了解决这类电路问题的普遍分析方法,即首先根据电路的回路连接关系,通过基尔霍夫定律写出回路方程,该方程是微分方程,只有电感或者只有电容时是一阶方程,同时存在两种元件时,是二阶方程,按照微分方程的求解,然后对结果给出物理解释。
RL电路以及RC电路的微分方程解中,含有指数函数,按照该指数函数的规律,这一项将随着时间逐渐衰减至0,表明电路中存在一种暂态过程,其影响程度随时间迅速减弱,解的另一部分是振幅与时间无关的项,表明电路最终趋向与一个稳定的状态,此时的电流称为稳态电流,它的振荡周期与施加的电源周期相同,而存在一定的相位差。
RLC电路的情况则比以上两者更为复杂,因为从求解微分方程的角度,二阶微分方程的解的形式比较复杂,从电路形式来说,LC电路上的电压并不能稳定在某一常数,通过借鉴矢量合成方法,用向量表示电流电压,可以比较清晰的揭示电路的物理意义,解算过程也相对简洁。该方法称为向量法,向量法在研究交流电路,进行交流电流和电压的分析求解时,相比传统的数学方法,有很强的优势。
通过进一步的研究二阶微分方程的求解方法,可以对RLC电路给出更普遍的数学公式,是本文的下一步工作。
[1]布达克.电路理论基础及应用[M].科学出版社,1985.
[2]E.卡姆克.常微分方程手册[J].1977.
[3]冯向莉.基于交流电路中平均值与有效值的分析[J].现代电子技术,2005,28(23):104-105.
[4]朱华光,朱玮玮.RLC串联谐振电路的实验研究[J].现代电子技术,2010,33(21):199-202.
[5]颜福才.按键消抖电路瞬态分析和设计[J].现代电子技术,2014(6):51-55.
TM13 【文献标识码】A 【文章编号】1009-5624(2018)02-0108-03

