基于联盟区块链的董事会电子投票系统
董友康,张大伟,韩臻,常亮
基于联盟区块链的董事会电子投票系统
董友康1,张大伟1,韩臻1,常亮2
(1. 北京交通大学计算机与信息技术学院,北京 100044;2. 桂林电子科技大学广西可信软件重点实验室,广西 桂林 541004)
董事会投票是特定范围的小集体为某一问题进行匿名表决的场景,对参与者的身份要求严格。设计了一种基于联盟链的董事会电子投票协议,用智能合约取代了传统的可信第三方,降低了系统信任成本;采用基于数字证书的身份准入机制,保证了参与投票者的身份合法性;基于椭圆曲线盲签名技术设计了电子投票协议,实现了投票的匿名性。安全分析表明,所提协议能够满足电子投票协议的安全性要求,使用方便灵活,提高了系统易用性。
区块链;联盟链;电子投票;盲签名
1 引言
电子投票协议是由Chaum[1]在1981年首先提出的,用于解决互联网环境下的选举和投票场景下的安全性问题,即满足投票的合法性、匿名性、计票完整性、不可伪造性、不可重复性、不可篡改性等要求[2]。为了解决上述问题,密码学家们经过30多年的研究,对电子投票技术已经有了较为成熟的解决方案,并应用于政府选举、董事会决策等领域。
使用匿名信道的电子投票协议的底层密码学技术主要分为盲签名、环签名、代理签名这3种。基于盲签名技术的电子投票协议主要分为有可信第三方(TTP, trusted third party)的投票协议和无可信第三方的投票协议2种。无TTP的投票协议最早是由Merrit[2]设计的,该协议所需执行的投票轮数与投票者数成正比,且计算量大。苏云学等[3]提出了一种方案,可以通过固定轮数进行匿名投票。有TTP的投票协议中,日本学者Fujioka等[4]提出的电子投票协议(简记为FOO协议)是最早大规模使用的基于盲签名的投票协议,是电子投票发展史上一个革命性的进步,它使电子投票得到了前所未有的发展。但其被证明无法实现不可伪造性,且存在共谋攻击的风险。后续有大量的基于FOO协议进行改进的工作,包括丛清日等[5]提出的电子投票方案中,解决了上述缺陷,但是在最后进行选票公布的时候,将投票者的ID签名和公钥同时公布,破坏了投票的匿名性。由于这些协议都存在TTP,要求投票者必须信任中央机构,且投票前必须设立这些中央机构。在这种情况下,用户无法察觉和防御计票机构和管理机构的共谋攻击。这些问题的存在增加了用户的使用代价,制约了电子投票技术的推广。
区块链在不引入第三方中介机构的前提下,可以提供去中心化、不可篡改、安全可靠等特性保证,可以看作一种无中心的TTP。比特币[6,7]是区块链技术的典型代表,链上数据一旦生成便无法篡改,并且全网公开可见,所以比特币可以看作一个全球范围的无中心的、分布式的TTP。联盟链是区块链技术发展的成果之一,联盟链[8,9]是具有准入机制的区块链,用户必须具备合法的身份才能加入联盟链中。联盟链可以看作一个特定范围的分布式TTP,具有较高的安全性和可信性,是解决董事会决策等特定范围投票需求的一种新解决思路[10]。
本文提出了一种基于联盟链的、使用椭圆曲线盲签名技术的董事会电子投票协议。该协议能够满足电子投票协议的6个安全要求,并且通过联盟链的智能合约实现了传统TTP的功能,增加了该协议的可信程度和适用范围。
2 电子投票系统
电子投票系统是以密码学原理为基础,使用计算机、互联网、通信等技术代替传统的人工方式来实现投票功能。通常,一个电子选举方案包含如下步骤[11]。
1) 申请。这个步骤是由合法的投票人从选举中心取得一个以后可以验证的标志信息。投票人的一些个人信息及投票人的投票信息都有可能隐藏在这个标志信息中。
2) 投票。投票人构造出合法的选票通过某种方式送给选举中心。
3) 统计。选举中心统计选票。
4) 验证。对于一个电子选举方案,其可验证性有个人可验证性和全体可验证性2种。个人可验证性指投票者本人能确认自己的选票被正确地统计在选举结果之中,而整体可验证性指任何人都可以根据公布出来的选举信息确认选举的统计工作的正确性。
电子投票协议为保证公平选举、防止欺骗,有6个安全要求,其具体含义如下[12]。
1) 合法性。只有经授权的投票者才能投票。
2) 匿名性。所有选票必须保密,每个人都不能知道他人的投票情况。
3) 计票完整性。所有选举者都能检验他们的选票在最后的表中是否被统计上。
4) 不可重复性。每一个投票人只能够投票一次。
5) 不可伪造性。任何人不能复制别人的选票。
6) 不可篡改性。任何人都不能修改他人的投票而不被发现。
3 基于椭圆曲线的盲签名算法
盲签名算法[13]是一个包含用户和签名者两方参与的密码协议。用户将盲化后的信息发送给签名者,签名者对该信息进行签名但是无法得到所签信息的具体内容。用户收到签名后的信息后对其进行脱盲,就能得到签名者对原始信息的签名,即使以后签名者见到这个消息时,也无法确定这是否是他签署的。盲签名算法可以有效地保护所签署消息或文件的具体内容,所以在电子投票这种需要匿名性的应用场合中起到了关键作用。
椭圆曲线密码体制(ECC, elliptic curve cryptography)是一种高效的密码体制,ECC的数学基础是椭圆曲线离散对数问题的难解性。张方国等[13]提出了一种基于椭圆曲线的盲签名算法,该方案可以看作是Schnnor盲签名在椭圆曲线上的模拟,能够实现弱盲签名。王化群等[14]在此基础上提出了强盲签名,本文设计的电子投票协议使用了文献[14]中的方案。其中算法参数设置如下。
(F):定义在有限域上的非奇异的椭圆曲线。
∈(F):曲线上的阶基点。
:有限域的元素个数,这里,或者=2。
上述参数中,保密,其他参数公开。
接下来,介绍算法的流程,其中记号(∙||∙)表示2个比特串连接,R()表示取点的坐标。
签名

其中,为原始消息,是盲化后的消息。用户将发送给签名者。
3) 签名者计算

为签名者对签名后的信息。然后,签名者将发送给用户。
4) 用户计算

得到原始信息的签名,(,)即为的盲签名。
验证
只需验证下式是否相等。

4 联盟链
区块链具有不可篡改、分布式存储、公开透明的特点,因此可以作为公布投票结果并防止篡改的公告板。联盟链[8]是一种具有身份准入机制的区块链,一个节点必须经过身份认证才能加入一条链中,通常由CA机构为节点颁发证书。区块链的节点之间通过共识机制达成信任,并提供节点间的匿名认证机制保护节点隐私。
智能合约[15,16]是运行在区块链上的、实现特定交易功能的一段程序,智能合约的代码和状态是公开的,链上用户可以对代码功能进行审核。联盟链中的智能合约语言是图灵完备的,并可与链外数据进行交互。智能合约一旦被部署到链上,就会一直运行且不可篡改。
因此,运行在联盟链上,具有特定的审核身份、审核选票、统计选票等业务逻辑的智能合约,能够取代传统的TTP,完成投票管理和统计功能,并满足其安全特性;而且,具有身份准入机制的联盟链能够满足董事会投票等特定范围投票场景的需求和身份审核要求;此外,联盟链中节点间的通信可采用安全信道,为投票系统中的传输安全提供更好的保障。因此,基于联盟链设计董事会电子投票协议较传统的基于TTP的方案在安全性和便利性方面更具优势。
5 联盟链董事会电子投票协议设计
本文采用盲签名算法,设计了基于联盟链的董事会电子投票协议,通过运行在联盟链上的具有管理和统计功能的智能合约取代了传统的TTP,实现了投票流程中的管理和计票功能,通过多方共识后写入账本的投票结果,能够满足用户的信任需求,减少用户的信任成本。通过使用盲签名方案,实现了票面信息的隐藏,防止攻击者利用系统漏洞破坏投票的匿名性。
5.1 参数说明
本协议使用的参数如下。
List1:投票记录表,由管理合约记录投票者申请签名的过程,防止投票者多次投票。
List2:计票信息表,由计票合约记录投票者投票信息,防止攻击者复制别人选票。
投票过程中的一系列计时器包括:
finishRegistration:注册截止时间,投票者在此时刻前完成注册;
beginvote:开始投票时间,投票者在此时刻后开始投票;
finishvote:结束投票时间,投票者在此时刻后完成投票;
5.2 系统设计
该系统中的角色有管理者、CA、投票者、管理合约、计票合约,角色的作用分别如下。
管理者:设定并公布投票者的名单、被投票的问题及选项、椭圆曲线参数、开始注册时间、开始投票时间及结束投票时间。
CA:为有投票权的用户颁发证书、为管理合约和计票合约颁发公私钥对。
管理合约:自动审核投票者身份、为盲化后的选票信息签名、将签名后的选票发送给投票者。
计票合约:自动计算选票、公布选票、公布投票结果。
本文方案的联盟链采用hyperledger fabric,系统架构如图1所示。
其中,CA通过fabric网络与投票者和智能合约进行通信,投票者向智能合约发送申请、投票等参数信息,合约接收到参数后自动执行相应的业务逻辑,并将执行结果写入区块链的账本中。
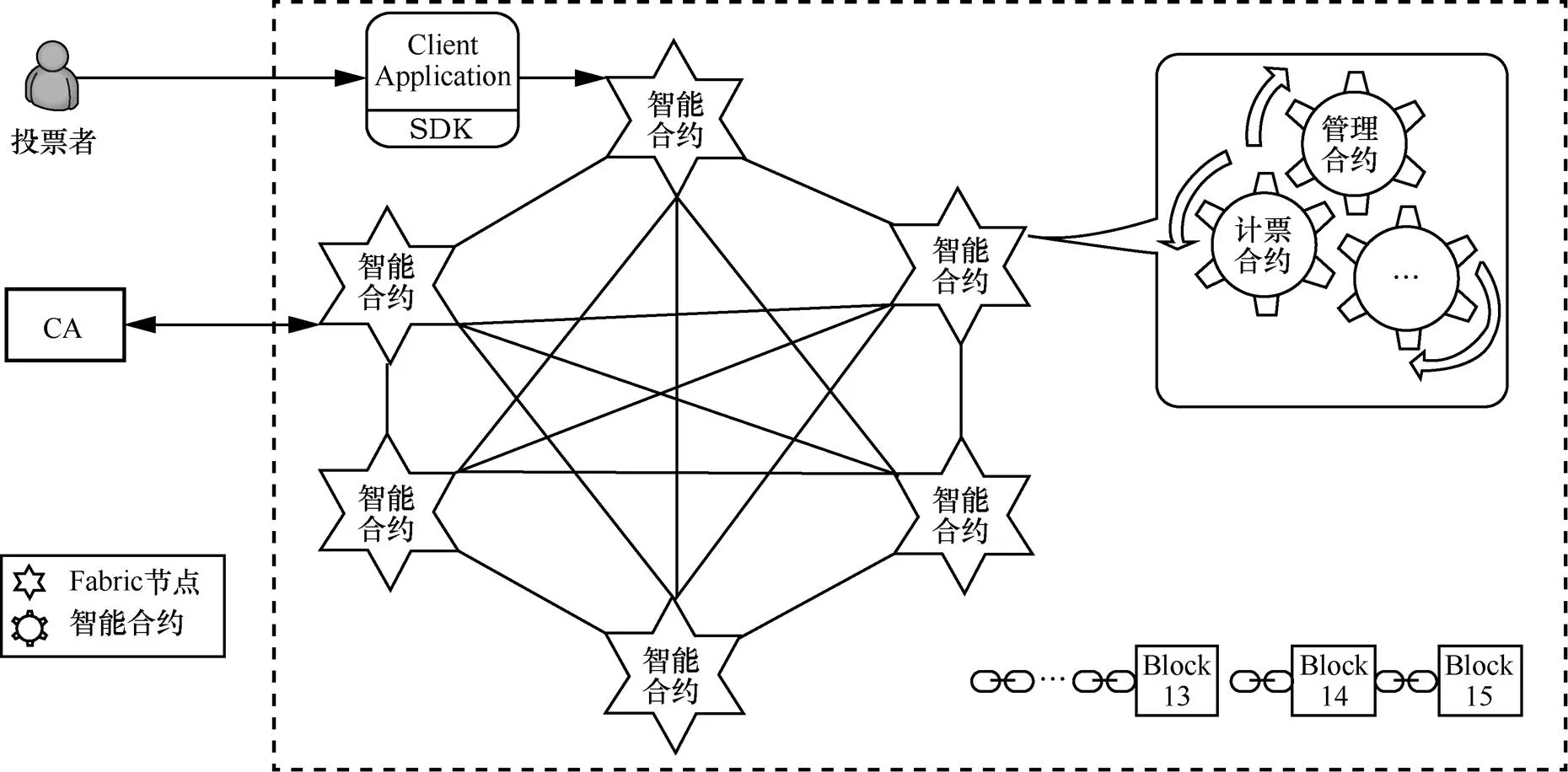
图1 投票协议架构

图2 投票协议时序
5.3 投票协议设计
投票协议分为5个步骤,协议的时序如图2所示。
5.3.1 初始化
管理者是由投票者共同选举出的,管理者设置选举过程用到的参数并公布。
2) 管理者设置计时器信息,用于通知投票者注册和投票的时间点。
4) 设置完成后,管理者公布上述参数,通知投票者开始注册,通知管理合约进入注册阶段。
5.3.2 注册
投票者向CA注册身份,CA为投票者颁发证书。同时,CA为管理合约和计票合约派发公私钥对。下述步骤对应图2中步骤1)~步骤5)。
1) 投票者V生成随机数x作为私钥,计算公钥y=xG。
2)V将{y,ID}发送给CA进行注册。
3) CA审查V身份,审查V是否有投票资格,审查通过后CA向V颁发实名证书Ecert。
4) CA生成管理合约的两对签名密钥对(X,Y)和(,),将X和通过安全信道发送给管理合约。本文的安全信道是通过TLS实现的,能够保护信息的机密性和完整性,具有实名认证和不可窃听的性质。
5) 管理合约生成投票记录表List1,列表由投票者证书和投票标志位组成,投票标志位用于标志用户是否申请签名,“0”表示尚未申请,“1”表示已经申请。List1的内容如表1所示。

表1 投票记录
6) CA生成计票合约的密钥对(X,Y),将X通过安全信道发送给计票合约。
注册阶段工作应在finishRegistration内完成。
5.3.3 生成选票的签名
投票者将投票信息进行盲化后发送给管理合约请求签名,管理合约对其进行签名后返回给投票者。下述步骤对应图2中的步骤6)~步骤9)。
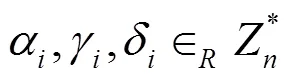

t=xmod

其中,v为原始选票消息,c是盲化后的选票。
3) 管理合约收到V发送的盲化选票后,检查证书的合法性。若证书非法,则拒绝签名。
4) 管理合约检查List1中Ecert对应的标志位是否等于0。若标志位为“1”,则拒绝签名。
5) 管理合约对盲化后的选票进行签名,即计算

然后将List1中Ecert对应的位置标志为1。
5.3.4 投票
投票者通过去盲得到原始选票的签名,然后生成正式选票,加密后匿名发送给计票合约。下述步骤对应图2中的步骤10)和步骤11)。

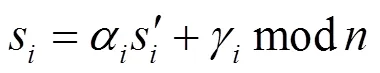
得到原始选票的签名。


生成正式选票。
3)V将正式选票m匿名发送给计票合约。
申请签名和投票工作在finishvote前完成。
5.3.5 计票并公布
计票合约解密选票后验证签名的有效性,检查投票是否已存在,然后统计选票生成最终投票结果,最后将投票结果写入账本并公布。下述步骤对应图2中的步骤12)和步骤13)。
1) 计票合约收到m,用私钥X进行解密,取出盲签名(c,s),验证签名是否来自管理合约,即计算

若相等,则签名通过验证;若不相等,则抛弃选票。
2) 计票合约取出c,在计票记录表List2中查询c是否存在。若存在,则抛弃选票;若不存在,则将c写入List2中。
3) 计票合约取出v并进行统计,得到投票结果。
投票流程结束。
6 安全性分析
6.1 盲签名方案的安全性分析
文献[13]中提出了盲签名方案的安全性证明过程,作者将签名的有效性规约到Schnorr盲签名方案的安全性保证,并将该方案的盲性规约到有限域上的椭圆曲线的离散对数难解问题。
6.2 投票协议的安全性分析
基于联盟链的董事会电子投票协议具有合法性、匿名性、不可重复性、不可伪造性、计票完整性、不可篡改性的安全特性,同时具备抗共谋攻击的能力。
1) 合法性
联盟链的CA可以实现用户的身份审核和准入机制,保证了加入链中进行投票的人都是合法的投票者。
2) 匿名性
本文从3个方面进行匿名性分析。

第二,投票者在申请签名过程中,通过无法窃听的安全信道与管理合约进行通信,能够防止Malice窃听。
第三,如果Malice节点能够读取智能合约的运行结果,Malice可以获得的信息用2个集合D、D表示,D是通过管理合约获得的信息,D是通过计票合约获得的信息。其中

此处分析表明,该方案满足匿名性。
3) 不可重复性
4) 计票完整性
5) 不可伪造性
Malice试图伪造一份选票,必须伪造管理合约的签名。此问题可以规约到签名算法的安全性,根据6.1节可知,Malice无法伪造签名。因此该方案满足不可伪造性。
6) 不可篡改性
7) 抗共谋攻击
智能合约本质上是运行在区块链上的具有特定业务逻辑的一段代码,智能合约的状态和内容是公开的,链上的用户都可以对代码进行审查,从而判断智能合约的功能。智能合约的运行结果都会写入账本并公开,而且不会做出开发者规定之外的行为。因此,协议中的管理合约和计票合约是安全可信的。
文中对于匿名性的分析也表明,即使管理合约和计票合约被攻击者窃听,获得2个合约的运行结果,攻击者也无法破坏匿名性。因此,该方案具有抗共谋攻击性。
7 结束语
本文介绍了一种基于联盟链的董事会电子投票协议,用特定业务逻辑的智能合约代替了传统的TTP。安全分析表明,该协议能够满足电子投票协议的安全要求,是安全可靠的。由于用户无需设立和信任TTP,只需加入联盟链中就可进行投票,因此降低了协议的实施成本,提高了协议的适用范围。
[1] CHAUM D. Untraceable electronic mail,return address,and digital pseudonyms[J]. Communications of the ACM, 198l, 28(2): 84-88.
[2] MERRITT M J. Cryptographic protocols[C]//The Fourteenth ACM Symposium on Theory of Computing. 1982: 383-400.
[3] 苏云学, 逯海军, 祝跃飞. 一个无需中央机构的电子投票协议[J]. 计算机工程, 2004, 30(11): 96-97.
SU Y X, LU H J, ZHU Y F. An electronic vote protocol without authority[J]. Computer Engineering, 2004, 30(11): 96-97
[4] FUJIOKA A, OKAMOTO T, OHTA K. A practical secret voting scheme for large scale elections[C]//Advances in Cryptology— Ausocrpt’92. 1993.
[5] 丛清日, 胡金初. 基于椭圆曲线盲数字签名的电子选举[J]. 计算机工程, 2010, 36(13): 156-158.
CONG Q R, HU J C. E-elections based on elliptic curve blind digital signature[J]. Computer Engineering, 2010,36(13):156-158.
[6] NAKAMOTO S. Bitcoin: a peer-to-peer electronic cash system[EB/OL]. http://bitcoin.org/bitcoin.pdf.
[7] 田海博, 何杰杰, 付利青. 基于公开区块链的隐私保护公平合同签署协议[J]. 密码学报, 2017, 4(2): 187-198.
TIAN H B, HE J J, FU L Q. A privacy preserving fair contract signing protocol based on block chains. [J]. Journal of Cryptologic Research, 2017, 4(2): 187-198.
[8] Hyperledger-fabricdocs documentation[EB/OL] http://hyperledger- fabric.readthedocs.io/en/latest/.
[9] KIAYIAS A, ZHOU H S, ZIKAS V. Fair and robust multi-party computation using a global transaction ledger[C]//The Annual International Conference on the Theory and Applications of Cryptographic Techniques. 2016: 705-734.
[10] MCCORRY P, SHAHANDASHTI S F, HAO F. A smart contract for boardroom voting with maximum voter privacy[C]// Financial Cryptography and Data Security. 2017.
[11] 龚俭, 陆晟, 王倩. 计算机网络安全导论[M]. 南京: 东南大学出版社, 2005: 144-147.
GONG J, LU C, WANG Q. Introduction to network security[M]. Nanjing: Southeast University Press, 2005:144-147.
[12] SCHNEIER B. Applied cryptography, second edition: protocols, algorithms, and source code in C[J]. Government Information Quarterly, 1997, 13(3):336.
[13] 张方国, 王常杰, 王育民. 基于椭圆曲线的数字签名与盲签名[J].通信学报, 2001(8): 22-28.
ZHANG F G, WANG C J, WANG Y M. Digital signature and blind signature based in elliptic curve[J]. Journal of China Institute of Communications, 2001(8): 22-28.
[14] 王化群, 张力军, 赵君喜. 基于椭圆曲线的Schnorr盲签名[J]. 计算机工程与设计, 2005, 26(7):1819-1822.
WANG H Q, ZHANG L J, ZHAO J X. Schnorr blind signature based on elliptic curve[J]. Computer Engineering and Design, 2005, 26(7): 1819-1822.
[15] SZABO N. Formalizing and securing relation-ships on public networks[DB/OL]. https://www.researchgate.net/publication/220167894_ Formalizing_and_Securing_Relationships_on_Public_Networks.
[16] KOSBA A, MILLER A, SHI E, et al. Hawk: the blockchain model of cryptography and privacy-preserving smart contracts[C]//Security and Privacy. 2016:839-858.
Board voting system based on the consortium blockchains
DONG You-kang1, ZHANG Da-wei1, HAN Zhen1, CHANG Liang2
(1. School of Computer and Information Technology, Beijing Jiaotong University, Beijing 100044, China;2. Guangxi Key Laboratory of Trusted Software, Guilin University of Electronic Technology, Guilin 541004,China)
The board voting is a scenario of anonymous voting on a particular group of individuals, which is strict with the identities of the participants. A board e-voting protocol based on the consortium blockchains was presented, which replaced the traditional trusted third party with the smart contract so as to reduce the system trust cost. It adopt a digital certificate-based identity mechanism to ensure that the voter's identity is legal. It adopt the blind signature based on elliptic curve technology to achieve the anonymity of voting. The security analysis shows that the proposed protocol can meet the requirements of unforgeability, anonymity and security etc, which is convenient and flexible to use.
blockchain, consortium blockchain, e-voting, blind signature
TP391.1
A
10.11959/j.issn.2096-109x.2017.00221
2017-11-15;
2017-12-03。
张大伟,dwzhang@bjtu.edu.cn
国家自然科学基金资助项目(No.61672091);广西可信软件重点实验室研究课题基金资助项目(No.KX201531)
The National Natural Foundation of China (No.61672091), Key Laboratory of Trusted Software Program of Guangxi Province (No.KX201531)
董友康(1993-),男,山西介休人,北京交通大学硕士生,主要研究方向为区块链、密码协议。

张大伟(1974-),男,辽宁朝阳人,博士,北京交通大学副教授,主要研究方向为智能卡安全、支付安全和区块链技术。
韩臻(1962-),男,浙江宁波人,博士,北京交通大学教授、博士生导师,主要研究方向为信息安全体系结构、可信计算。

常亮(1980-),男,贵州赫章人,博士,桂林电子科技大学教授,主要研究方向为知识表示与推理、可信计算。

