基于旋量理论的三指机器人灵巧手逆运动学分析

裴九芳 许德章 王 海

安徽工程大学机械与汽车工程学院，芜湖，241000

基于旋量理论的三指机器人灵巧手逆运动学分析

裴九芳 许德章 王 海

安徽工程大学机械与汽车工程学院，芜湖，241000

为提高三指机器人灵巧手逆运动学的求解效率，提出了基于旋量理论的逆运动学新的求解算法。以Shadow三指灵巧手为例，在无法直接利用单纯的Paden-Kahan 子问题求解逆运动学的条件下，食指(无名指)的逆解采用Paden-Kahan子问题与代数解相结合的算法，拇指的逆解采用数值法与Paden-Kahan子问题相结合的算法。最后通过计算实例证明了算法的有效性和可行性。该算法在保证精度的前提下，几何意义明显，耗费时间短，效率高。

旋量理论；灵巧手；逆运动学；Paden-Kahan子问题

0 引言

机器人灵巧手的逆运动学分析是根据各手指末端的期望位置，求解出各手指关节的转角。机器人灵巧手的运动学逆解是其控制和抓取规划的前提和基础，求解算法直接影响抓取效率和控制效果。

利用旋量理论建立的机器人运动学模型，其机器人的逆运动学问题可以转化为几类Paden-Kahan子问题进行求解，所得逆解是解析解，没有累计误差，实时性高，具有明显的几何意义和数值稳定性，简化了机器人运动学的分析和计算。SARIYILDIZ等[5]基于螺旋理论，以四元数为螺旋运动算子，解决了常见结构机器人的运动学逆解。TAN等[6]对Paden-Kahan子问题2进行扩展，并将其用于某种特殊结构的逆运动学求解。钱东海等[7]基于旋量理论，采用经典消元理论和Paden-Kahan子问题相结合的方法对六自由度的机械臂进行了逆运动学求解，该方法具有较强的通用性。陈庆诚等[8]针对具有特殊结构的六自由度机械臂，提出了“绕3个不相交轴旋转”的新的逆解子问题求解算法。孙恒辉等[9]针对一种后3个旋转关节轴线相交于一点、前3个旋转关节轴线均不相交的6R串联机器人，提出了一种新的 Paden-Kahan 子问题并进行了求解。吕世增等[10]基于吴方法的特征列思想，结合旋量法，对6R工业机器人进行了高效的逆解求解运算。李盛前等[11]引入希尔维斯特结式法对6R工业机器人进行逆运动学求解。

目前常见的Paden-Kahan子问题组合需要各关节轴线具有较多的交点，无法适用于所有多关节机器人结构的逆解问题。本文以Shadow 三指灵巧手为例，食指(无名指)采用Paden-Kahan子问题与代数解相结合的算法求得逆解，拇指则采用Paden-Kahan子问题与数值解相结合的算法。最后通过实例证明了该算法的正确性。该算法在保证精度的前提下，计算量小、效率高。

1 基于旋量理论的运动学模型

当一刚体既绕轴线ω(ω∈R3)转动(转动角度为θ)，又沿平行于ω轴方向移动(移动线速度为v)，如图1所示，则刚体的变换可以用矩阵指数形式表示为

(1)

(2)

v=-ω×q

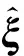
图1 刚体的旋量运动Fig.1 Screw motion of a rigid body

ω=0时

ω≠0时

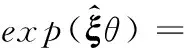
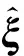
(3)

n自由度任意开链机器人的运动学正解映射可表示为gst:se(3)→SE(3)，其中，se(3)和SE(3)分别为李代数和李群，代表旋量的集合和刚体变换的集合，则机器人运动学正解的指数积公式为

(4)

2 机器人灵巧手的运动学逆解算法

2.1 运动学逆解的3个Paden-Kahan子问题

Paden-Kahan子问题的主要思想是：将复杂的机器人运动学逆解分解为若干个具有明确几何意义的逆解子问题，然后逐一解决，即将复杂的运动分解为几个连续的简单运动(都可采用运动旋量的指数积来表示)。 Paden-Kahan子问题主要有3种。

θ=arctan(ω·(u′×w′),u′·w′)

图2 Paden-Kahan子问题1Fig.2 Paden-Kahan sub problem 1

图3 Paden-Kahan子问题2Fig.3 Paden-Kahan sub problem 2

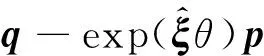
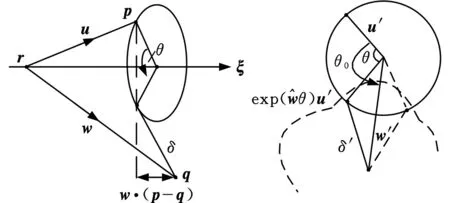
图4 Paden-Kahan子问题3Fig.4 Paden-Kahan sub problem 3

2.2 Shadow 三指机器人灵巧手手指逆运动学解的实现

2.2.1 Shadow三指机器人灵巧手结构

如图5所示，Shadow三指机器人灵巧手包括拇指、食指、无名指、简易手掌。拇指共5个自由度，分别为下指节的侧摆和屈曲、中指节的侧摆和屈曲，以及上指节的屈曲运动，其中，侧摆轴与屈曲轴垂直，且与手掌相连。食指和无名指结构相同(故下面逆运动学只分析食指)，分别为下指节的侧摆和屈曲，以及中指节和上指节的屈曲运动，其中，中指节和上指节相互耦合，耦合系数为1。

图5 Shadow灵巧手结构简图Fig.5 Schematic diagram of Shadow dexterous hand

2.2.2食指逆运动学逆解算法的实现

图6 食指的运动模型Fig.6 Motion model of the index finger

gst(θ)=

(5)

ci=cosθisi=sinθii=1,2,3,4

c23=cos(θ2+θ3)s23=sin(θ2+θ3)

c234=cos(θ2+θ3+θ4)s234=sin(θ2+θ3+θ4)

根据运动学正解结果，对食指逆解求解步骤如下：

(1)求θ1。令式(5)的第一行、第四列元素c1(a1+a2c2+a3c23+a4c234)=px，第二行、第四列元素s1(a1+a2c2+a3c23+a4c234)=py，则可得

θ1=arctan(py,px)

(6)

即

(7)

式(7)中仅有未知数θ3，利用子问题3可解出θ3。

(3)求θ4。θ4和θ3相互耦合，耦合系数为1，则

θ4=θ3

(8)

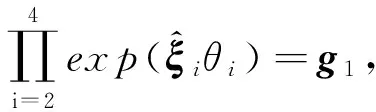
(9)

利用子问题1对式(9)进行求解，即得θ2。

2.2.3拇指逆运动学解算法实现

由拇指的运动模型简图(图7)可知，拇指的特点是关节1与关节2的轴线相交，a1=0，关节3与关节4轴线相交，关节1、关节4与关节5轴线平行，垂直纸面向外。这种结构是无法利用已有的3个子问题直接求解而获得逆解的。为了提高求解效率，应尽量计算各关节的解析解；如果不能够获得解析解，以尽少采用数值解为宜。根据拇指的特点，设计的求解过程如下。

图7 拇指的运动模型Fig.7 Motion model of the thumb

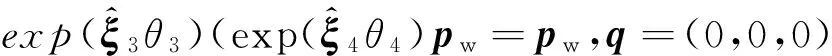
(10)

对式(10)两边右乘pw，则

(11)

(12)

式(12)中只有一个未知数θ5，利用数值解解得即可。

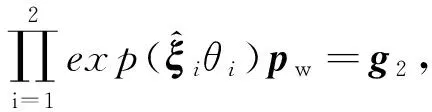
(3)求θ3和θ4。因θ1、θ2和θ5已知，将式(10)左边的θ1、θ2移至等式右边，则式(10)变为

(13)

3 逆解实例计算验证

参照人手各个关节的转动范围，表1给出了Shadow灵巧手手指结构参数和关节范围。

表1 Shadow灵巧手手指结构参数和关节范围

根据食指和拇指的逆运动学算法，其验证方法和步骤如下：

(1)给定手指各关节确定的角度。

(2)根据灵巧手手指的正运动学方程计算出手指指尖在此角度下的位姿。

(3)应用本文提出的食指和拇指的逆运动学算法逐步求解各关节的角度。在多解的情况下，将所解关节角范围外的角度剔除。

(4)比较步骤(1)中给定角度和步骤(3)中求解的角度，若二者误差在允许范围内，则验证本文算法正确；否则不正确。

根据此步骤，在关节取值范围内任意选取一组数据，则食指和拇指的求解结果如表2所示。 通过比较理论设定值和实际运行结果各对应元素的数值，关节角运行误差最大为食指的第三和第四关节，皆为0.0444°，最小运行误差为食指的第一关节，数值为0°，可以看出，本文提出的手指逆解的算法具有较高的精度，同时在该算法中，食指(无名指)的逆解算法都为解析解，而拇指仅第五关节需要数值解，其余都为解析解，改进了传统的D -H逆解算法中食指(无名指)和拇指都需要数值解，计算量大、效率低的问题。对算法运行时间进行统计，本文仿真软件采用MATLAB2011，计算机CPU为i5-4590@3.3GHz，内存为8G的64位Win7操作系统。表3是利用旋量理论与D -H方法所得逆解的各运行时间。可以看出，利用旋量理论效率较D -H方法高。说明利用旋量理论进行求逆的算法耗费时间少，计算效率高，证明该算法是正确有效的。

表2 逆解求解结果

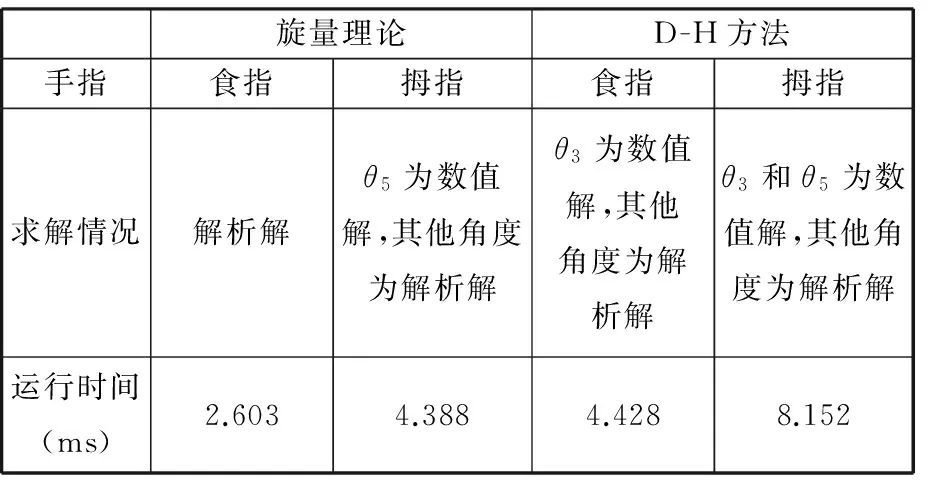
表3 旋量理论与D -H方法所得逆解

4 结语

应用旋量理论建立了Shadow 三指(拇指、食指、无名指)灵巧手各指的运动学模型，针对各手指不同的结构，提出采用Paden-Kahan子问题与代数解结合求解食指(无名指)的逆解，采用数值法与Paden-Kahan子问题相结合求解拇指逆解，这两种求解算法，整体计算量小，提高了计算效率；拇指和食指求逆的过程利用了Paden-Kahan几何算法，并利用了轴的交点、轴外点等几何量进行计算，几何特征明显；通过实例计算，验证了该逆解算法的可行性与有效性。

[1] DENAVIT J，HARTENBERG R S. A Kinematics Notation for Lower Pair Mechanisms Based on Matrices [J].Journal of Applied Mechanics，1995，21(5):215-221.

[2] LEE R，YAN Honglin. Development of Universal Environment for Constructing 5-axis Virtual Machine Tool Based on Modified D-H Notation and OpenGL[J]. Robotics and Computer-Integrated Manufacturing，2010，26(3): 253-262.

[3] ROCHA C R，TONETTO C P，DIAS A. A Comparison between the Denavit-Hartenberg and the Screw-based Methods Used in Kinematic Modeling of Robot Manipulators[J]. Robotics and Computer-Integrated Manufacturing，2011，27(4):723-728.

[4] 张玉茹，李继婷，李剑锋. 机器人灵巧手—建模、规划与仿真[M]. 北京：机械工业出版社， 2007.

ZHANG Yuru，LI Jiting，LI Jianfeng. Dexterous Robot Hand—model Planning and Simulation[M]. Beijing: China Machine Press，2007.

[5] SARIYILDIZ E，TEMELTAS H. Solution of Inverse Kinematic Problem for Serial Robot Using Quaternion[C]//Proceedings of the IEEE International Conference on Mechatronics and Automation. Changchun: IEEE，2009: 26-31.

[6] TAN Yuesheng，XIAO Aiping. Extension of the Second Paden-Kahan Sub-problem and Its’ Application Kinematics of a Manipulator[C]// Proceedings in the Inverse of the International Mechatronics Conference on Robotics Automation. Chengdu: IEEE，2008: 379-381.

[7] 钱东海，王新峰，赵伟，等.基于旋量理论和Paden-Kahan子问题的6自由度机器人逆解算法[J]. 机械工程学报，2009，45(9):72-76.

QIAN Donghai， WANG Xinfeng，ZHAO Wei，et al. Algorithm for the Inverse Kinematics Calculation of 6-DOF Robots Based on Screw Theory and Paden-Kahan Sub-problems[J]. Journal of Mechanical Engineering，2009，45(9):72-76.

[8] 陈庆诚，朱世强，王宣银，等. 基于旋量理论的串联机器人逆解子问题求解算法[J]. 浙江大学学报:(工学版)，2014，48(1):8-14.

CHEN Qingcheng，ZHU Shiqiang，Wand Xuanyin，et al. Inverse Kinematics Sub-problem Solution Algorithm for Serial Robot Based on Screw Theory[J]. Journal of Zhejiang University(Engineering Science)，2014， 48(1): 8-14.

[9] 孙恒辉，赵爱武，李达，等. 基于新旋量子问题改进一类6R串联机器人逆解算法[J]. 机械工程学报， 2016，52(1):79-86.

SUN Henghui，ZHAO Aiwu，LI Da， et al. Improvement of the Algorithm of the Inverse Kinematics Calculation for 6R Series Robots Based on One Novel Paden-Kahan Sub-problem[J]. Journal of Mechanical Engineering，2016，52(1):79-86.

[10] 吕世增，张大卫，刘海年. 基于吴方法的6R机器人逆运动学旋量方程求解[J]. 机械工程学报，2010，46(17): 35-41.

LYU Shizeng，ZHANG Dawei，LIU Hainian. Solution of Screw Equation for Inverse Kinematics of 6R Robot Based on Wu’s Method[J]. Journal of Mechanical Engineering，2010，46(17):35-41.

[11] 李盛前，谢小鹏. 基于旋量理论和Sylvester结式法的6自由度机器人逆运动学求解分析[J]. 农业工程学报，2015，31(20):48-54.

LI Shengqian，XIE Xiaopeng. Analysis of Inverse Kinematic Solution for 6R Robot Based on Screw Theory and Sylvester Resultant[J]. Transactions of the Chinese Society of Agricultural Engineering，2015， 31(20):48-54.

[12] HUNT K H. Kinematic Geometry of Mechanisms [M]. New York: Oxford University Press，1978.

InverseKinematicsAnalysesof3-fingerRobotDexterousHandBasedonScrewTheory

PEI Jiufang XU Dezhang WANG Hai

School of Mechanical and Automotive Engineering,Anhui Polytechnic University,Wuhu,Anhui,241000

A novel inverse kinematics algorithm was proposed based on screw theory in order to improve operation efficiency of inverse kinematics for 3-finger robot dexterous hand. Taking Shadow 3-finger robot dexterous hand as an example, because inverse kinematics might not be solved directly by Paden-Kahan sub problem, an inverse solution of index finger(ring finger) was combined with algebraic solution and Paden-Kahan sub problem. The inverse solution of thumb was combined with numerical method and Paden-Kahan sub problem. Finally, validity and feasibility of the algorithms were proved by an example. Under the premise of ensuring accuracy, the algorithms have obvious geometric meaning, less computation, and high efficiency.

screw theory; dexterous hand; inverse kinematics; Paden-Kahan sub problem

TP242

10.3969/j.issn.1004-132X.2017.24.013

2016-11-22

国家自然科学基金资助项目(51175001)；安徽工程大学优秀青年人才基金资助重点项目(2013RZR001zd)

(编辑张洋)

裴九芳，女，1980年生。安徽工程大学机械与汽车工程学院副教授。主要研究方向为机器人灵巧手的抓取规划、机器人控制等。发表论文15篇。E-mail :jfpei@ahpu.edu.cn。许德章，男， 1964年生。安徽工程大学机械与汽车工程学院教授。王海，男，1976年生。安徽工程大学机械与汽车工程学院教授。