基于转角的迭代学习控制策略下永磁同步电机EPS转矩脉动抑制方法

赵林峰 陈久闪 陈无畏 张荣芸

1.合肥工业大学汽车与交通工程学院，合肥,2300092.博世汽车部件(苏州)有限公司，苏州,2150213.安徽工程大学机械与汽车工程学院，芜湖，241000

基于转角的迭代学习控制策略下永磁同步电机EPS转矩脉动抑制方法

赵林峰1陈久闪2陈无畏1张荣芸3

1.合肥工业大学汽车与交通工程学院，合肥,2300092.博世汽车部件(苏州)有限公司，苏州,2150213.安徽工程大学机械与汽车工程学院，芜湖，241000

建立了基于永磁同步电机( PMSM)的电动助力转向(EPS)模型。由于PMSM固有的非正弦磁通分布、齿槽效应和电流检测误差等因素导致了明显的转矩脉动，因此根据寄生转矩脉动多是转子位置的周期函数和EPS系统中电机转速并非恒定不变的特点，提出了一种基于转角的迭代学习控制算法来抑制EPS中PMSM的转矩脉动，并对此进行了大量的仿真和实验验证。实验结果表明，该方案对EPS转矩脉动具有显著的抑制效果。

永磁同步电机；电动助力转向；迭代学习控制；转矩脉动

0 引言

近年来，电动助力转向(electric power steering，EPS)系统被广泛应用于汽车上。永磁同步电机(permanent magnet synchronous motor，PMSM)因其体积小、损耗低、效率高等优点，尤其适合在对空间和节能方面要求严格的汽车上使用。然而，在管柱助力型EPS中PMSM通过减速机构直接与转向管柱相连，电机的振动和转矩脉动直接经方向盘传递到驾驶员手上，因此，为了改善驾驶员手感和提高行驶安全性，必须对助力电机的转矩脉动进行抑制[1]。

目前，很多学者研究了转矩脉动最小化的问题，这些方法主要分为改进永磁同步电机设计与改进控制方法两大类。通过改进电机设计来削弱转矩脉动的方法主要有斜槽法、斜极法、改进定子绕组形式法、改进定子和转子磁路法等[2-4]，这些方法能有效地减小齿槽转矩和纹波转矩。然而，这些方法均会增加电机的制造难度和成本，同时还会降低电机的性能。近年来，随着微电子技术和新型电机控制理论的发展，通过运用各种方法控制定子电流的波形以抑制转矩脉动的方法越来越受到人们的重视。这些方法主要有反电势倒置法、编程电流控制法、反馈控制法、智能控制法、PWM(pulse width modulation)调制方式控制法以及自适应控制法等[5-10]。反馈控制方法通过转矩和磁链观测器来产生反馈信号，从而削弱转矩脉动，但其控制精确度会受到电机参数变化的影响，并且不能有效消除电机参数变化所带来的转矩脉动，使得控制效果变差[6]。智能控制方法和自适应控制方法虽然在一定程度上克服了电机参数时变的影响，但实现复杂，在目前技术条件下的实用性也不强，因此有必要考虑从其他方面对电机转矩脉动进行补偿。

永磁同步电机转矩脉动的组成主要有：齿槽转矩、谐波转矩、电流增益误差和逆变器死区效应等，其中绝大部分转矩脉动都具有周期性的特点[4]。因此，迭代学习控制(iterative learning control，ILC)作为一种重复控制方法非常适合来抑制这些转矩脉动[11]。当前，诸多学者在将迭代学习控制应用于永磁同步电机转矩脉动抑制时，总是需要获知给定的电机转速，因为作为一种基于记忆的控制方法，ILC的记忆长度必须要与转矩脉动的周期相匹配。但在EPS系统中，电机转速并非恒定不变的，速度的变化会破坏ILC记忆长度与转矩脉动周期的匹配关系，限制了ILC在EPS中永磁同步电机上的应用。为了解决这一问题，本文在分析永磁同步电机转矩脉动的基础之上，提出了基于转角的迭代学习控制算法，并对其在EPS上的应用效果进行了仿真和实验验证。

1 采用永磁同步电机的EPS模型

设永磁同步电机d、q轴电感系数为Ld、Lq，相电阻为R，永磁体磁链常数为ψf，d、q轴磁链分量分别为ψd、ψq，np为磁极对数，d、q轴电流分量分别为id、iq，ωr为转子机械角速度，电机输出的电磁转矩为Tm，则定子磁链方程为

(1)

输出力矩方程为

(2)

为了获得最大的输出转矩，提升永磁同步电机运行效率，本文在矢量控制中采取id=0的控制方式。此时，电机电磁转矩与其交轴电流iq成线性关系，通过对iq的调节，实现对电机输出转矩的调节控制，磁场定向矢量控制具体流程如图1所示。

图1 永磁同步电机矢量控制框图Fig.1 Permanent magnet synchronous motor vector control block diagram

本文研究的转矩脉动抑制问题主要针对EPS系统中的永磁同步电机，将所建立的电机模型加入到EPS系统动力学模型中，即

(3)

Ts=Ks(θs-θe)

(4)

(5)

(6)

式中，Td为转向盘转矩；Ts为转矩传感器检测的转矩；Tm为电机负载转矩；Ks为扭矩传感器的扭转刚度；Js为转向盘和输入轴总的转动惯量；Bs为输入轴阻尼系数；θs为转向盘转角；θe为输出轴的转角；gm为减速机构(蜗轮蜗杆)的减速比；Tp为输出轴作用在齿轮上的转矩；Je为输出轴转动惯量；Be为输出轴的黏性摩擦系数；rp为小齿轮节圆半径；mr为齿条质量；xr为齿条位移；Br为等效齿轮齿条阻尼系数；Kr为等效弹簧刚度。

2 转矩脉动分析

2.1 齿槽效应

齿槽转矩由转子上安装的永磁体与定子铁心之间的磁引力而产生，磁引力的圆周分量试图保持定子齿与永磁体一系列固定位置的对齐，因此齿槽转矩Tcog可定义成永磁体磁场能量关于转子相对机械角度θm的负导数，同时可以看出，即使电机未励磁，齿槽转矩仍然存在，即

(7)

根据文献[12]的分析，可得到齿槽转矩关于转子机械角θm的公式：

(8)

式中，leff为铁心的有效长度；μ0为空气磁导率；Ri和Ro分别为气隙的内外半径；z为定子齿槽数；Br为磁通密度；Br,k为Br傅里叶级数展开系数;n为使nz/(2np)为整数的值；G为气隙相对磁导率；Gn为G的傅里叶级数展开系数。

2.2 磁通谐波

磁通谐波是永磁同步电机另一个产生转矩脉动的主要原因。在实际的永磁同步电机中，磁通密度分布并不是呈理想正弦形式的，当其与正弦的定子电流相互作用时便会产生周期性的转矩波动。在静止的 ABC三相坐标系下，磁链谐波主要包含了5次、7次等高次谐波。变换到旋转dq坐标系下，谐波表现为6次、12次及6的整数倍分量。因此，电磁转矩可以表示为

(9)

式中，Ψ0为基波磁链d轴分量的幅值；Ψ6、Ψ12分别为6次、12次谐波磁链d轴分量的幅值。

从式(9)可以看出电机电磁转矩分为两部分：一部分是q轴电流与磁通基波分量的乘积，另一部分即是随电角度(一对磁极在空间转过的角度称为电角度)变化的谐波转矩，其中磁链的6次、12次谐波分量是影响转矩波动的主要因素，因θe=npθm，故谐波转矩脉动亦可看作是电机转子机械转角的周期函数。

综上所述，永磁同步电机电磁转矩中除了直流分量，还含有基波和2次、6次以及6的整数倍次的谐波分量，并且均是关于电机机械转角的周期函数。

3 迭代学习控制

3.1 迭代学习控制原理

针对重复运动的被控对象，ILC 利用控制系统先前的控制经验，以及反复的迭代修正，以测量系统的实际输出和期望输出的偏差为参考，来不断修正控制信号，使其向理想的控制信号逼近，最终抑制了周期性扰动。相比于其他控制方法，该方法具有以下优点：迭代学习控制能够修改控制信号，意味着它无需改变被控系统的结构，同时也对设备参数不敏感。通常使用的迭代学习控制算法如下：

ui+1(k)=(1-α)ui(k)+Γei(k)+Φei+1(k)

(10)

式中，ui(k)为系统控制输出量；i为当前迭代次数；k=0，1，…，N-1为相对于当前迭代周期起始时间的时间标志，并且N代表整个迭代周期所分成的份数；ei(k)为电机输出电磁转矩的实际值与给定值之差；Φ为前一时间间隔内迭代过程产生的误差信号对本次迭代过程影响的增益系数，也称闭环学习增益；Γ为本次迭代过程产生的误差信号对本次迭代过程影响的增益系数，也称开环学习增益；α为遗忘因子。

迭代学习控制能有效执行还需满足以下几个条件[13]：①系统在有限的固定时间间隔上运行；②期望轨迹给定且已知；③系统的初始状态和初始条件不变；④系统结构在迭代运行中不变；⑤系统输出状态可测；⑥存在且唯一存在一个理想控制输入使得系统的状态和输出满足期望轨迹。

3.2 传统迭代学习控制

对于EPS系统，即使传统迭代学习控制满足以上的限制条件也不能有效地抑制转矩脉动。因为对于传统迭代学习控制，其迭代周期必须要和转子旋转一周的时间相等(或者是转子旋转一周时间的整数倍)。这就意味着电机转速必须保持恒定，而在EPS系统中电机转速总是随转向盘转速变化而发生变化，具体分析如图2和图3所示。图2、图3中，x轴为时间，y轴为转子机械转角，同时假定二者具有相同的迭代周期且第一个旋转周期与迭代周期相同。从图2可以看出，由于转速保持恒定，接下来的转子旋转周期仍然与迭代周期相等。在图3中，t1、t2、t3、t4表示在不同的迭代次数下,与各个迭代初始时刻具有相同时间间隔所对应的时间点,这些点在不同迭代周期中拥有相同的时间位置，因此，这些点所对应的转子位置是相同的。由前文分析可知，转矩脉动是关于转子转角的函数，因此，这些点记录了同样的转矩脉动信息。这也是基于时间的迭代学习控制能够在恒定电机转速下抑制转矩脉动的原因。

图2 恒转速下迭代时电机转角Fig.2 Motor angle iteration under constant speed

图3 变转速下迭代时电机转角Fig.3 Motor angle iteration under variable speed

在图3中，由于电机转速的变化，除了第一个转子旋转周期外，其他旋转周期均小于迭代周期，t1、t2、t3、t4这些点对应着不同的转子位置，因此，在此类工况下，基于时间的迭代学习控制算法就无法对电机转矩脉动进行有效抑制。

4 基于转子位置的迭代学习控制

4.1 基本原理

在EPS中,由于电机转速无法保持恒定，因此传统基于时间的迭代学习控制无法有效抑制转矩脉动,但是，通过对永磁同步电机转矩脉动的分析可知，它与电机转子位置直接相关。因此，式(10)中的时间变量k可以用转子位置θm代替，即

ui+1(θm)=(1-α)ui(θm)+Γei(θm)+Φei+1(θm)

(11)

因为转矩脉动是转子位置的周期函数，无论电机转速(即转向盘转速)怎么变化，转矩脉动与转子位置的关系不会改变，因此，基于转子位置的迭代学习控制算法能够用于对EPS系统中永磁同步电机转矩脉动的抑制。

(12)

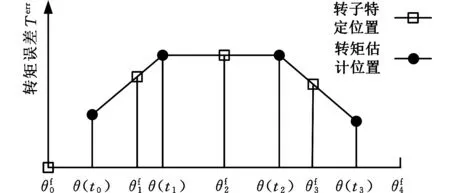
图4 差值计算原理Fig.4 The difference between calculation principle

4.2 永磁同步电机迭代学习控制

本文采用永磁同步电机矢量控制与基于电机转子位置的迭代学习控制相结合的控制方法，具体如图5所示，图中，Kt=npΨd。迭代学习控制器的输入信号是转矩期望值Tmr与转矩观测器计算得到的实际转矩值Tm的差值信号，而迭代学习控制器的输出Δiq作为电流调节器的前馈补偿。在每一个迭代控制周期中，通过Δiq对参考q轴电流iqr进行补偿，通过控制实际输出转矩实现对期望转矩的跟踪，来达到有效抑制系统转矩脉动的目的。

图5 永磁同步电机迭代学习控制Fig.5 Iterative learning control of permanent magnet synchronous motor

学习律收敛与否是迭代学习控制器设计时需要考虑的重要问题之一，要想使所设计的迭代学习控制有实际效果，必须保证迭代学习过程收敛，才能使系统输出逐渐趋近于期望轨迹，每次迭代的输出误差逐渐减小。对本文所设计的迭代学习控制算法的收敛性分析如下。

在基于永磁同步电机的EPS系统中，迭代学习系统输出即为定子的补偿电流Δiq，则学习律可以表示为

Δiq,k+1(θm)=
(1-α)Δiq,k(θm)+Γek(θm)+Φek+1(θm)

(13)

设

(14)

则

(15)

(16)

其中，Δiq,k为第k次迭代输出的补偿电流。则

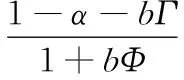
(17)

要想系统收敛，则必须满足：

(18)

设常数项满足：

(19)

则

|ek+1|=|λek+ρk|≤|λ(λek-1+ρk-1)|+|ρi|≤

|λ2ek-1|+|λρk-1|+|ρk|≤…≤|λk+1e0|+|λkρ0|+

|λk-1ρ1|+…+|λρk-1|+|ρk|≤|λk+1e0|+|λk|ρmax+

(20)

若bΦ>0,由式(18)可知：

|1-α-bΓ|<1

(21)

进而得到

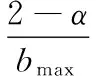
(22)

考虑控制器鲁棒性，遗忘因子α常取0.05～0.10之间的值；开环学习增益Γ值与收敛速度成正相关，故应取Γ接近(2-α)/bmax；闭环学习增益Φ不宜选取过大，否则会导致在时滞存在的情况下系统失稳。

5 仿真与实验

为了验证所提出的控制策略对转矩脉动的抑制效果，本文从仿真和实验两方面对基于时间与基于转角两种迭代学习控制策略的控制效果进行了对比。

首先，定义FTR为转矩脉动系数，如下式所示：

(23)

式中，Tmax为转矩脉动最大值；Tmin为转矩脉动最小值；Tav为平均输出转矩。

转矩脉动系数反映了电机输出转矩在目标值附近波动的剧烈程度。

5.1 仿真结果

仿真计算中所利用的永磁同步电机参数、EPS机械结构参数如表1所示。

同时，综合考虑迭代学习控制器的收敛条件、收敛速度和转矩脉动系数，将迭代学习控制器仿真参数设计为：Φ=0.04，Γ=0.02，α=0.1。

表1 永磁同步电机参数和EPS系统参数Tab.1 Parameters of PMSM and EPS system parameters

为了验证本文所提出的迭代学习控制算法相对于传统迭代学习控制算法在电机变转速下对转矩脉动抑制的有效性，在电机转速闭环模型中对两种算法进行仿真。设定期望转速初始值为50 r/min，每隔2 s阶跃变化一次，每次增加10 r/min，电机负载为3 N·m，采样时间为100 μs，获得电机转速波动情况分别如图6和图7所示。

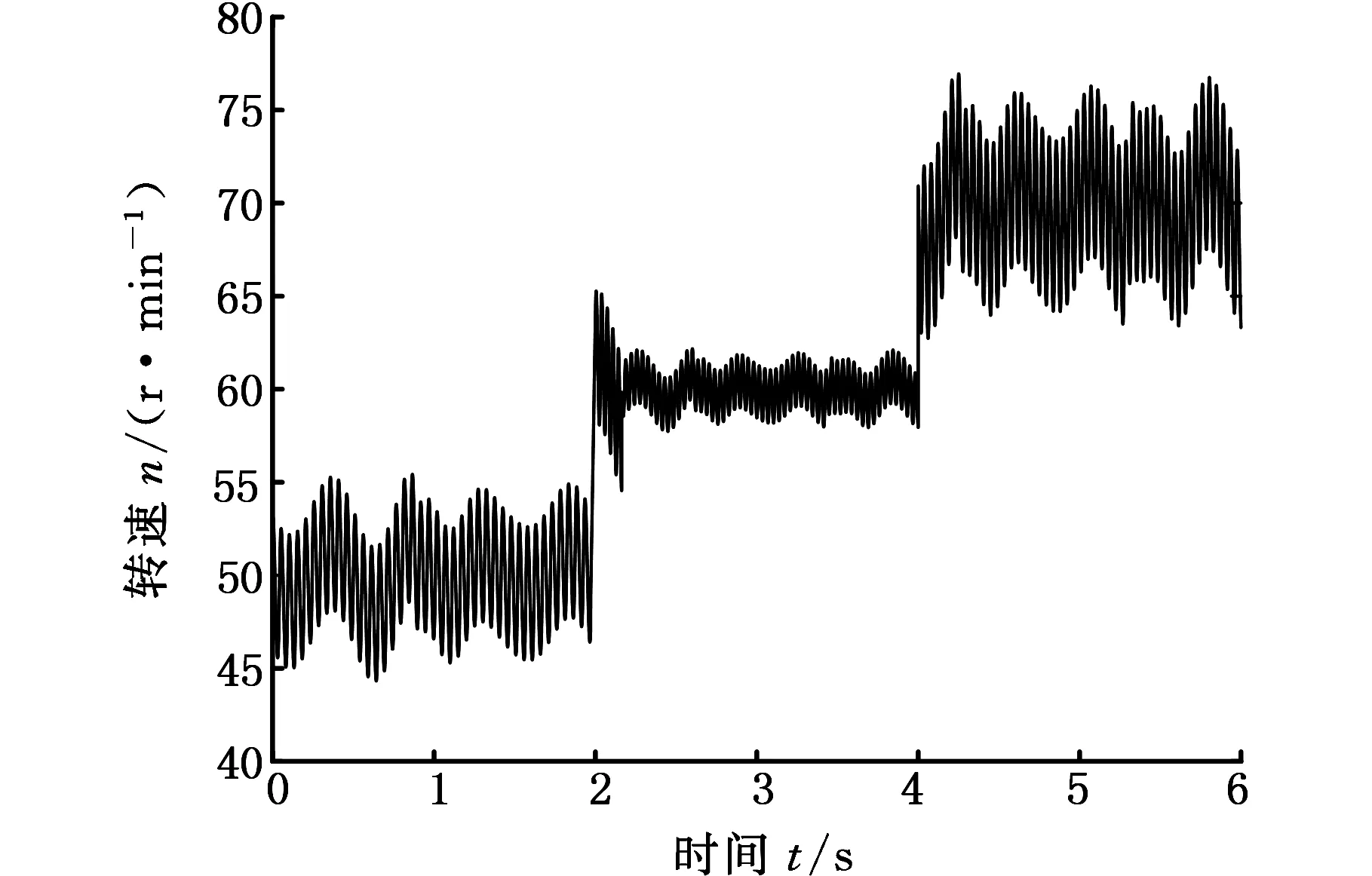
图6 基于时间迭代学习控制Fig.6 Time based iterative learning control

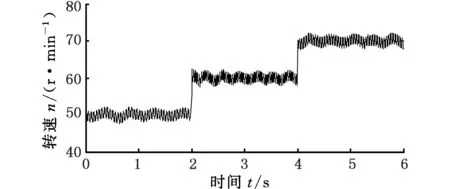
图7 基于电机转子位置的迭代学习控制Fig.7 Iterative learning control based on motor rotor position

仿真结果表明，基于电机转子位置的迭代学习控制算法在各个转速下均能有效地对电机转矩脉动进行抑制，而传统迭代学习控制算法只有在电机处于特定转速(60 r/min)时才能抑制电机转矩脉动，在非特定转速下，由于算法会对q轴电流误补偿，所以甚至会增大电机的转矩脉动，恶化系统性能。

调整转向盘输入转矩使其分别为1 N·m和3 N·m，在0.4 s时引入基于电机转子位置的电流迭代学习补偿控制，图8和图9为补偿前后转矩的响应曲线。

图8 输入转矩为1 N·m时转矩输出Fig.8 Torque output by 1 N·m input on steering wheel

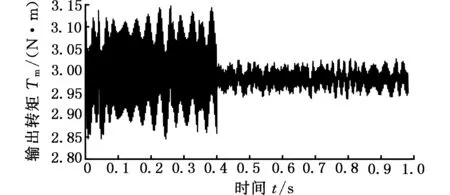
图9 输入转矩为3 N·m时转矩输出Fig.9 Torque output by 3 N·m input on steering wheel

可以看出在引入电流迭代学习补偿控制后，转向盘输入转矩为1 N·m时，永磁同步电机转矩脉动系数从10.8%下降到了3.2%；方向盘输入转矩为3 N·m时，电机转矩脉动系数从23.6%下降到了8.7%，从上文的分析也可以看出，EPS系统转矩脉动在轻载慢速时影响更为严重，但所设计的控制算法仍能有效抑制转矩脉动，控制效果明显。

5.2 实验结果

为了验证本文所设计的基于转角的迭代学习补偿控制策略对EPS系统的转矩脉动抑制效果，与仿真结果进行对照，在EPS试验台进行了验证实验，如图10所示。利用工控机上编写的Labview程序发送模拟的转矩信号到EPS控制器，分别控制转向盘输入转矩为1 N·m和3 N·m的恒定助力转矩，启动EPS控制器3 s后运行迭代学习控制算法程序，转矩响应曲线如图11和图12所示。

图10 EPS试验台Fig.10 EPS test bench

图11 1 N·m恒转矩输入时台架试验转矩响应Fig.11 Torque response of bench test for 1 N·m constant torque input

对比控制算法在前文仿真计算与台架试验中的转矩脉动效果如表2所示。从表2可以看出，仿真与台架试验中电机转矩都在期望转矩附近呈上下波动，符合之前的理论分析，并且与仿真模拟结果具有相同特性，加入控制算法后转矩脉动系数降低，转矩脉动得到抑制，虽然抑制效果与理想状态下仿真计算的结果存在一定的差距，但是所设计的迭代学习控制算法依然有效地抑制了电机转矩脉动。

图12 3 N·m恒转矩输入时台架试验转矩响应Fig.12 Torque response of bench test for 3 N·m constant torque input

为了进一步模拟汽车行驶过程中转向盘转矩输入，利用工控机的Labview发送特定的转矩信号到EPS转矩传感器，控制助力电机输出幅值为4 N·m、周期为10 s的正弦波助力转矩。图13、图14分别是采集到的有无采取迭代学习控制时的电机输出转矩图。

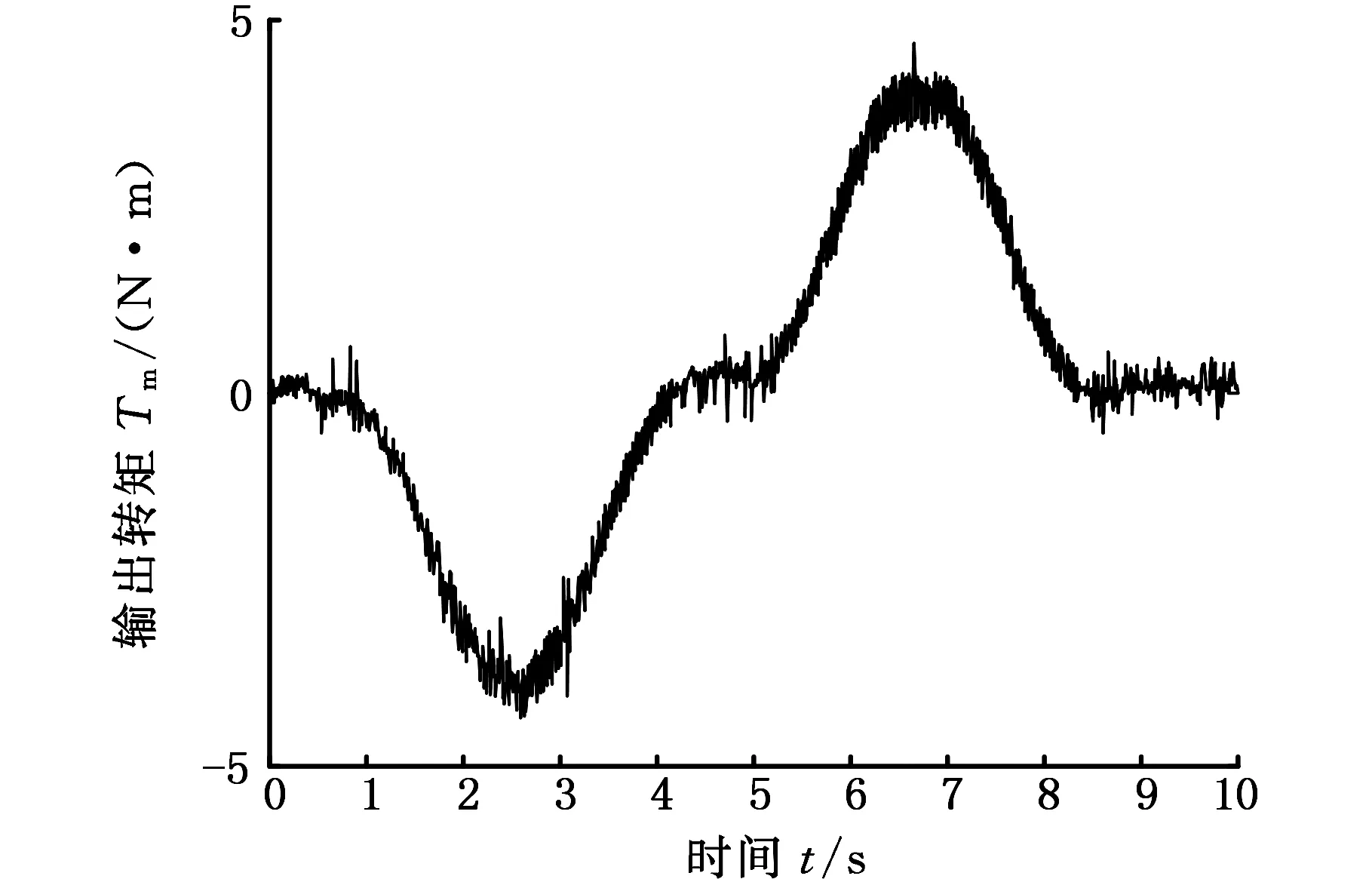
图13 无迭代学习控制电机转矩输出Fig.13 The output torque of the motor without iterative learning control

图14 迭代学习控制电机转矩输出Fig.14 The output torque of the motor with iterative learning control

从图13和图14可以看出，在排除信号采集过程中因干扰而产生的毛刺的情况下，EPS控制器在运行迭代学习控制程序后对系统转矩脉动起到了一定的抑制效果。

6 结论

(1)对于传统迭代学习控制，其迭代周期必须要和转子旋转一周的时间相等，由于EPS系统的永磁同步电机转速并不固定，故该方法在EPS上的应用被限制。为抑制永磁同步电机在转速变化时的转矩脉动，本文采用永磁同步电机矢量控制与基于电机转子位置的迭代学习控制器相结合的控制方法。

(2)建立了采用永磁同步电机作为助力电机的EPS动力学仿真模型，从仿真和实验两方面对比了基于时间与基于转角两种迭代学习控制策略的控制效果。实验结果表明，基于转角的迭代学习控制策略相对于基于时间的迭代学习控制策略能更好地解决变转速时永磁同步电机转矩脉动问题。

[1] LEE S H, LEE G H, KIM S I, et al. A Novel Control Method for Reducing Torque Ripple in PMSM Applied for Electric Power Steering[C]//Electrical Machines and Systems, ICEMS 2008 International Conference on IEEE. New York,2008:3142-3145.

[2] 郁亚南，黄守道，成本权,等. 绕组类型与极槽配合对永磁同步电动机性能的影响[J]. 微特电机，2010，38(2)：21-23.

YU Yanan, HUANG Shoudao, CHENG Benquan, et al. Influence of Winding Type and Slot-pole Combination on the Performance of Permanent Magnet Synchronous Motor[J].Micro Motor,2010，38(2)：21-23.

[3] ZHU Z Q, HOWE D. Influence of Design Parameters on Cogging Torque in Permanent Magnet Machine[J]. IEEE Trans. on Energy Coversinon,2000,15(4):404-417.

[4] 郭宏,钱浩. 永磁同步电机低转矩脉动的稳健设计[J]. 中国电机工程学报,2012,32(24):88-95.

GUO Hong, QIAN Hao. Robust Design of Permanent Magnet Synchronous Motor with Low Torque Ripple[J].Chinese Journal of Electrical Engineering,2012,32(24):88-95.

[5] 姚哲之，易灵芝. 基于三电平逆变器的直接转矩控制研究[J]. 计算技术与自动化，2008，27(4)：40-43.

YAO Zhezhi, YI Lingzhi. Research on Direct Torque Control Based on Three Level Inverter [J].Computing Technology and Automation，2008，27(4)：40-43.

[6] 王宏佳，杨明，牛里,等. 永磁交流伺服系统电流环带宽扩展研究[J]. 中国电机工程学报，2010，30(12)：56-62.

WANG Hongjia, YANG Ming, NIU Li, et al.Research on Current Loop Bandwidth Expansion of Permanent Magnet AC Servo System [J].Chinese Journal of Electrical Engineering，2010，30(12)：56-62.

[7] 孟光伟,李槐树,熊浩. PWM调制下无刷直流电机的转矩脉动抑制[J]. 电气传动,2011(1):26-30.

MENG Guangwei, LI Huaishu,XIONG Hao. Torque Ripple Suppression of Brushless DC Motor under PWM Modulation [J].Electric Drive,2011(1):26-30.

[8] 周美兰,高肇明,吴晓刚,等. 五种PWM方式对直流无刷电机系统换相转矩脉动的影响[J]. 电机与控制学报,2013,17(7):15-21.

ZHOU Meilan, GAO Zhaoming, WU Xiaogang, et al. Influence of Five PWM Modes on Commutation Torque Ripple in Brushless DC Motor [J]. Journal of Electrical Machinery and Control,2013,17(7):15-21.

[9] 王大方,卜德明,朱成,等. 一种减小无刷直流电机换相转矩脉动的调制方法[J]. 电工技术学报,2014,29(5):160-166.

WANG Dafang, BU Deming, ZHU Cheng, et al. A Method of Reducing Commutation Torque Ripple in Brushless DC Motor[J].Journal of Electrical Engineering,2014,29(5):160-166.

[10] LUH J Y S, FISHER W D, PAUL R P C. Joint Torque Control by a Direct Feedback for Industrial Robots[J]. IEEE Transactions on Automatic Control,1983,28(2):153-161.

[11] 李书臣，李平，徐心和，等. 迭代学习控制理论现状与展望[J]. 系统仿真学报，2005，17(4)：904-908.

LI Shuchen, LI Ping, XU Xinhe, et al. Current Status and Prospect of Iterative Learning Control Theory [J]. Journal of System Simulation，2005，17(4)：904-908.

[12] 宋伟，王秀和，杨玉波. 削弱永磁电机齿槽转矩的一种新方法[J]. 电机与控制学报，2004，8(3)：214-217.

SONG Wei, WANG Xiuhe, YANG Yubo. A New Method for Reducing Cogging Torque of Permanent Magnet Motor [J]. Journal of Electrical Machinery and Control，2004,8(3)：214-217.

[13] ARIMOTO S, NANIWA T, SUZUKI H. Robustness of P-type Learning Control with a Forgetting Factor for Robotic Motions [J]. IEEE Conference on Decision&Control,1990,5(1):2640-2645.

TorqueRippleSuppressionofPMSMAppliedforEPSBasedonMotorRotationAngle’sILC

ZHAO Linfeng1CHEN Jiushan2CHEN Wuwei1

1.School of Automotive and Transportation Engineering, Hefei University of Technology, Hefei,230009 2.BOSCH Automotive Components (Suzhou) Co., Ltd., Suzhou, Jiangsu,215021 3.School of Mechanical and Automotive Engineering, Anhui Polytechnic University, Wuhu, Anhui,241000

An EPS model was established based on PMSM. Due to factors such as the inherent non-sinusoidal magnetic flux distribution, cogging effects and current detection errors of PMSM, obvious torque ripples were caused. According to the characteristics that parasitic torque ripples were mostly a periodic function of the rotor position and the motor speeds in EPS system were not constant, an ILC algorithm based on corners was proposed to suppress the torque ripples of EPS in PMSM, and a large number of simulations and experimental verifications were carried out.The experimental results show that this scheme has significant inhibitory effects on the torque ripples of EPS.

permanent magnet synchronous motor (PMSM); electric power steering(EPS);iterative learning control (ILC); torque ripple

2016-07-21

国家自然科学基金资助项目(51375131,51675151,51605003)

U463.4

10.3969/j.issn.1004-132X.2017.24.002

(编辑王艳丽)

赵林峰，男，1979年生。合肥工业大学汽车与交通工程学院副教授、博士。主要研究方向为车辆动力学与控制。发表论文20余篇。E-mail: zhao.lin.feng@163.com。陈久闪，男，1992年生。博世汽车部件(苏州)有限公司工程师。陈无畏，男，1951年生。合肥工业大学汽车与交通工程学院教授、博士研究生导师。张荣芸，男，1985年生。安徽工程大学机械与汽车工程学院讲师。