基于Voronoi图与Delaunay三角网的杉木人工纯林林木补植位置与空间配置

赵春燕，李际平

（中南林业科技大学，湖南 长沙 410004）

基于Voronoi图与Delaunay三角网的杉木人工纯林林木补植位置与空间配置

赵春燕，李际平

（中南林业科技大学，湖南 长沙 410004）

杉木人工纯林被划归为生态公益林，为了提高物种多样性，在杉木纯林内补植阔叶树种是多功能经营的一种有效手段。为了在杉木人工纯林林木补植时尽可能优化林分空间结构，本文提出基于Voronoi图与Delaunay三角网的补植位置与空间配置方法。以林木个体所在空间位置为平面相异点构建Voronoi图和Delaunay三角网，Voronoi图量化对象木的K-阶邻近关系，Delaunay三角网确定相邻木间的距离、角度和林木间的林隙。考虑林分的水平空间结构，选取基于Voronoi图的变异系数、混交度和竞争指数分别描述林木的分布格局、混交程度和竞争关系，建立林木和林分空间结构调控的均质性目标。林木补植前进行两株萌生木与枯死木的抚育间伐，补植分两次进行，第一次补植栾树，马褂木，第二次补植观光木，依据林木间Delaunay三角形面积大小确定林木补植位置，依据K阶邻近林木关系进行补植林木的空间配置,以达到林分空间结构优化的目的。因为研究对象为杉木人工纯林，补植前林分的树种混交度很低，介于0.011～0.063，由于属于杉木幼龄，还没有郁闭，竞争指数介于0.699～0.833，竞争强度较小，基于V图的林木分布变异系数介于1.662～2.354；林木补植后林分树种混交度得到提高，第二次补植后树种混交度（0.191±0.007）比第一次补植后的树种混交度（0.186±0.005）有所提高，均明显大于补植前树种混交度（0.042±0.020），补植后不仅物种多样性增强，树种混交程度增强；补植后竞争指数增大，第二次补植后林分竞争指数（4.67±0.32）比第一次补植后林分的竞争指数（4.41±0.24）有提高，均大于补植前林分的竞争指数（3.92±0.20），表明补植后竞争强度增强；第二次补植后基于Voronoi图的变异系数（0.48±0.07）比第一次补植后基于Voronoi图的变异系数（0.55±0.10）降低，均小于补植前基于Voronoi图的变异系数（2.04±0.31），表明补植后空间分布更均匀。基于Delaunay三角网进行林木补植能够调整林木的空间分布，基于K阶邻近的林木补植空间配置能够尽可能提高补植林木混交度与林分混交度，且补植树种越多，混交度越大，本文提出的林木补植方法可以实现林木补植在提高生物多样性同时优化林分空间结构。本研究为林分空间结构调整与优化林木补植提供理论依据，促使杉木人工纯林导向近自然林，实现多功能的森林经营。

Voronoi图；林木补植；生态公益林；杉木人工纯林；空间结构优化

2001年，湖南省按照国家公益林认定办法（林策发[2001]88号）开展了公益林区划工作，共区划公益林453.1万hm2，占全省林地面积的35.0%，其中杉木人工纯林所占比重较大，区划之前为用材林，林分结构简单，功能单一，主要为提高木材收获量[1]。为了发挥生态公益林维护和改善生态环境、保持生态平衡、保护生物多样性等功能，有必要对杉木人工纯林进行空间结构调控[2-5]。通过补植乡土阔叶树种，增加物种多样性同时优化空间结构，这是多功能经营的要求[6]。

在杉木人工纯林内，通过适当的抚育间伐和阔叶林补植，能够加强生物多样性保护，突出生态功能的作用。林木补植优先选择在较大的“林隙”内[7]，但是针对不同的补植密度，如何依据“林隙”大小的排序确定林木最适合的补植位置？

Voronoi图是按照对象集合中元素的最近邻原则将空间划分成多个区域，是对空间的一种剖分[8]。以林分中单株木构建Voronoi图，图中任意一个凸多边形代表林木的“影响圈”，反映林木间相互作用及其对环境适应的结果。Voronoi图具有唯一对偶结构Delaunay三角网，Delaunay三角网包含相邻木间的距离和角度信息。Brown在1965年将Voronoi图应用于林学与生态学，提出林木竞争分析的APA指数，国内，汤孟平等[9]最先应用Voronoi图确定对象木的相邻木，分析种内种间关系与混交隔离程度，赵春燕等[10]应用Voronoi图和Delaunay三角网结构量化林分空间结构，刘帅等[11]建立了基于Voronoi图的林分空间模型，在此基础上分析林木整体空间格局。大量研究表明Voronoi图和Delaunay三角网量化与分析林分空间结构具有可行性，但目前主要应用在研究对象木的最近邻木，确定林分空间结构单元。

本文以生态公益林杉木人工纯林为研究对象，利用Voronoi图和Delaunay三角网结构，挖掘其林学与生态学意义；借助Voronoi图和Delaunay三角网结构研究林木补植位置与空间配置的方法，通过补植乡土阔叶树种，增强物种多样性的同时尽可能优化林分空间结构，实现杉木人工纯林的多功能经营。

1 研究区概况

福寿林场位于湖南省平江县，东经113°41′～ 113°45′、 北 纬 28°30′～ 28°32′， 地 处 罗 霄 山连云山支脉，南高北低，平均海拔1 204 m，平均坡度为22～27°。该区域位于中亚热带向北亚热带的过渡带，属大陆季风性气候，年平均气温12.1℃，土壤属于花岗岩山地黄壤。

研究区域属中亚热带常绿阔叶林植被区，群落较多，有木本植物55科，275种。该地区林分的优势树种为杉木Cunninghamia lanceolata，长期人工造林与经营，目前已被划归为生态公益林。

2 研究方法

2.1 样地设置与样地调查

在研究区域的杉木人工纯林内，选取6年生的杉木幼龄林，设置6个20 m×30 m的标准地，编号T1～T6，3个样地（T1～T3）进行林木补植，3个样地（T4～T6）作为对照。

每个样地以西南角为起点，测量其经纬度，用罗盘仪围测样地边界，用皮尺量斜距，按坡度改算为水平距。要求闭合差不大于1/200，样地间保留至少20 m的缓冲区。对样地内胸径大于2.0 cm的林木每木检尺，调查样地内每株林木的树种类型，相对西南角的位置坐标（以30 m长边为X轴，20 m短边为Y轴）、胸径和树高等测树因子。

2.2 以单株木构建Voronoi图与Delaunay三角网

以N个单株木作为平面上相异点，基于场论观念，N个单株木相互“竞争”将平面的空白区域剖分，每个林木的“影响区域”通过竞争以中剖分达到平衡，按照最邻近原则划分平面，基于单株木构建Voronoi图具有“全覆盖、零重叠”的特征，且能够量化对象木的K-阶邻近关系[12]（图1）。

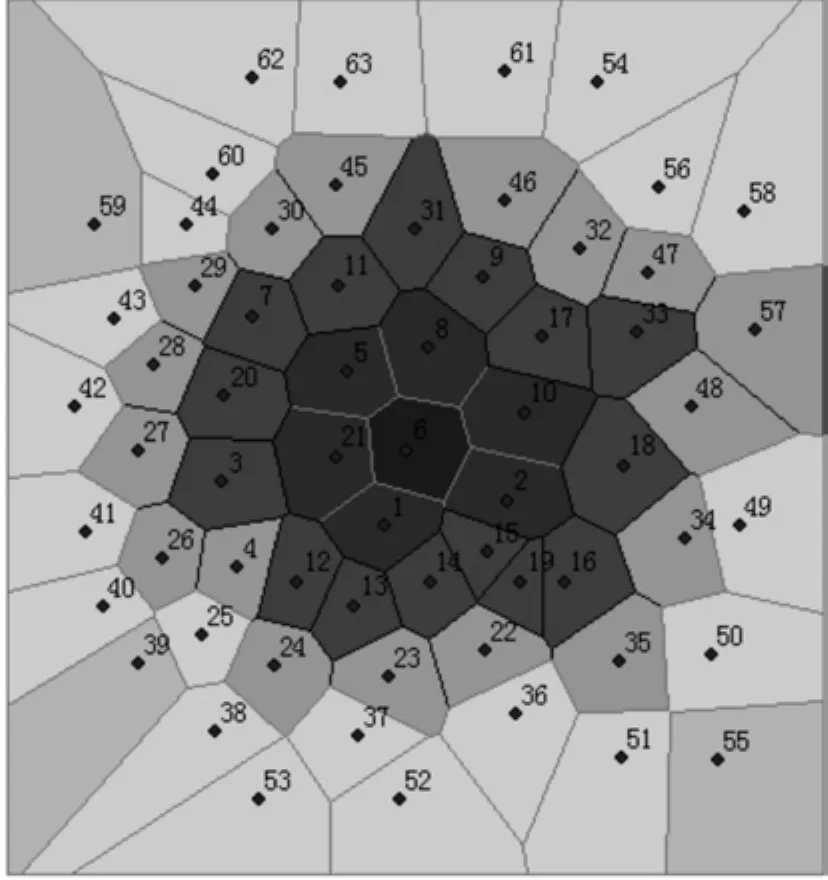
图1 基于Voronoi图对象木的K-阶邻近关系Fig.1 Object wood K-neighboring relationship based on Voronoi diagram

与相邻Voronoi多边形共享边的相关点连接构成Delaunay三角形，是Voronoi图的唯一对偶结构，单个Delaunay三角形包含相邻林木间的距离和角度信息。

2.3 空间结构指数

（1）混交度

混交度选取汤孟平等[13]提出的物种多样性，计算公式为：

式中：Mi为对象木i的混交度，n为最近邻木株数，ni为最近邻木的树种数，当对象木i与第j株相邻木非同种时Vij=1，反之，Vij=0。

（2）竞争指数

竞争指数采用Hegyi指数(1974)，计算公式为：

式中：Dj为对象木i第j个相邻木的胸径，Di为对象木i的胸径，DISTij林木i与林木j之间距离。

（3）基于Voronoi图的变异系数

由林木个体构建的Voronoi图多边形面积表示林木的影响范围，变异系数（CV）表示Voronoi多边形面积的标准差与平均值的比值，CV可以表示林木的空间分布特征[14]。

式中，xi为第i个Voronoi多边形的面积，为所有Voronoi多边形的平均面积，n为样地内林木株数。

2.4 空间结构调控目标

在森林景观中单元同质、单元间明显异质作为林分划分的一个主要依据，依据森林景观斑块均质性原理，本文采用李建军等[15-16]提出的森林生态系统空间结构调控的均质性目标。

本文只考虑水平空间结构，选取基于Voronoi图的变异系数（CV）、混交度和竞争指数分别描述林木的分布格局、混交和竞争关系[17-18]，汤孟平等[19]研究表明，较优的空间结构具有较高混交度、较低竞争指数和较均匀的空间分布。为消除量纲的影响，各个指数分别除以样地空间结构指数均值。因此，林木空间结构均质性指数（Li）计算公式为：

式中，Li为林木空间结构均质性指数，Mi与为补植第i株林木混交度与样地混交度均值，CIi与为补植第i株林木竞争指数与样地竞争指数均值，Wi与为补植第i株林木角尺度与角尺度均值。

为了反映林分整体的均质性特征，林分空间均质性指数采用林分内所有林木的均质性指数的平均值。

2.5 杉木人工纯林林木补植位置

依据林分空间结构调整与优化的目标，林分内林木呈现均匀分布或偏向均匀的随机分布。林木补植的位置应在相对大范围的“林隙”，基于Voronoi图构建单株木的Voronoi多边形，每个凸多边形表示林木的影响范围，也表示林木周围的这种“林隙”，结合Delaunay三角网中Delaunay边长表示相邻木之间的距离。因此，林木补植位置的步骤为：

第1步：以单株木构建Voronoi图和Delaunay三角网，标记以样地边界为Voronoi凸多边形的边的林木，进行边缘校正；

第2步：选取面积最大Delaunay三角网Di，林木补植的位置为Delaunay三角网Di的内心；

第3步：计算补植林木的空间密度指数Di，如果空间密度指数大于设定的空间密度指数阈值，补植完成，否则，从第2步开始循环。

式中，ri为参照树包含相邻n株邻近木时的最小半径，rmax在林分中相邻两株林木的最大距离。

林木补植的数量用林分密度进行控制，因为本文研究区域为杉木人工纯林，采用株数密度计算林分的密度。

2.6 基于K-阶邻近杉木人工纯林林木补植的空间配置

林木补植树种选择适合当地地形与气候等环境的乡土阔叶树种，补植的位置与补植数目确定后，接下来需要解决补植林木的空间配置，空间配置影响林分混交度与林木之间的竞争。依据林分空间结构调整与优化的目标，因为补植林木均为胸径4～4.5 cm的林木，每一补植位置树种选择的依据就是尽可能大的混交度。

若依据确定补植的树种为Tj种，标记为T1，T2，…，TW，为了提高林分内树种的隔离程度，补植树种的空间配置方案如下：

第1步：以林木补植所有补植位置和现有林木构建Voronoi图和Delaunay三角网，任意选择一个已确定的林木补植位置Di；

第2步：依据林木补植中心点Di的Voronoi凸多边形，记录1-阶相邻木数量n，统计相邻木的树种类型（T1，T2，…，Tm）及各树种出现的次数为STi，且满足补植树种选择相邻木中出现比例最低的，仅依据此在1-阶相邻木中往往不能确定补植树种，此时需要考虑K-阶邻近，在K-阶邻近中选择出现比例最低的；

第3步：把Di标记为已补植，在Di的K-阶邻近范围内，选择K值最小且待补植的位置记为Di，循环第2步，直到所有的补植位置都已标记为已补植。

3 结果与分析

3.1 林木补植之前的空间结构特征

研究对象为6年实生的杉木人工纯林，但存在大量萌生的柳杉，样地的平均胸径为2.85～4.27 cm，加权平均树高为2.49～3.35 m，因为样地海拔较高，划归为生态公益林没有进行经营。林木之间平均距离为1.95～2.52 m，林木的平均影响范围为4.33～5.99 m2，因为初始种植密度为2 m×2 m，部分林木枯死或被伐除。

表1 林分基本特征Table 1 Stand basic information

因为研究对象为杉木人工纯林，混交了一部分萌生的柳杉，林分混交度很低，介于0.011～0.063。竞争指数介于0.699～0.833，竞争强度较小，主要因为研究对象为杉木幼龄林，还没有形成郁闭。基于V图的林木分布变异系数介于1.662～2.354，呈现比较均匀的空间分布。

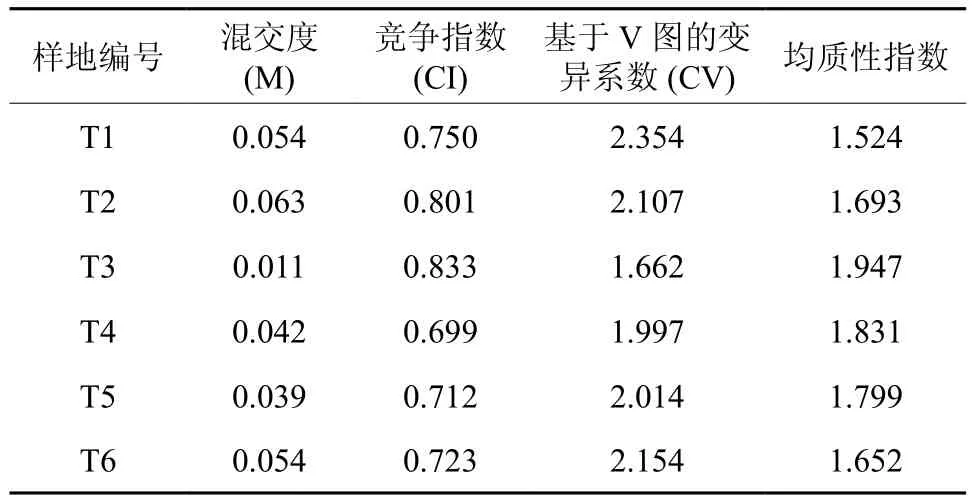
表2 林分空间结构特征Table 2 Spatial structure of forest stands

3.2 林木补植数量与补植位置

王怀芳[20]研究生态公益林杉木人工林林分密度为1 050～2 500株/hm2，样地（20 m×30 m）内为63～150株。因为样地内为杉木幼龄林，海拔较高，为了提高物种多样性和混交度，提高补植乡土树种的比例，3块作业样地通过两次补植到180～188株，补植前对双株萌生的林木和枯死木进行抚育间伐。

图2为样地T1抚育间伐和林木补植的模拟图，图2A中采伐林木为萌生木，样地第一次的实际补植在2014年2—3月，补植位置依照图2B中提供的位置进行补植，补植的树种为栾树，马褂木，其中栾树的平均胸径为4 cm，马褂木的胸径为4.5 cm；样地第二次补植在2015年3月，依照图2C提供的位置进行补植，补植的树种为观光木，平均胸径为4 cm。

图2 补植位置示例Fig.2 Replanting location sample

3个补植样地间伐萌生木和枯死木，保留115～125株杉木或柳杉，按照1∶1比例，第一次补植栾树与马褂木，补植后样地140～148株林木，第二补植观光木，补植后样地180～188株林木。补植后，邻木之间平均距离介于1.49～2.12 m，比补植前平均距离减少了7%～23.5%，但补植林木数量为补植前林木总数量的48.00%～56.52%。基于Voronoi多边形的平均面积介于3.01～4.99 m2，表明林木的平均影响范围为3.01～4.99 m2，比补植前减少了20.04%～43.85%。因为林木补植位置一般位于面积较大的Voronoi多边形内，补植林木的相邻木Voronoi多边形被分隔，面积较大的Voronoi多边形被分隔，而面积较小的Voronoi多边形对应林木分布较密集，补植前后Voronoi多边形的面积最小者没有变化。

3.3 补植林木的空间配置

补植林木的数量与位置确定后，不同补植树种的比例与空间配置导致树种不同的隔离程度，补植树种的胸径、树高和冠幅不同，补植后对邻近林木竞争关系有不同的影响。

在示范样地进行了两次补植，栾树、马褂木和观光木的补植比例为1∶1∶2，补植林木的平均胸径为4～4.5 cm。为了增强树种混交度，在杉木幼龄纯林内选择单株混交的方式。考虑林木K阶邻近[12]，按照图3示例的方法进行补植。

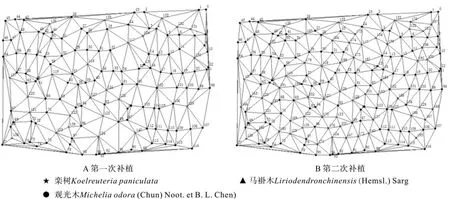
图3 补植林木的空间配置示例Fig.3 The sample of replanting trees spatial con figuration

3.4 补植前后的空间结构特征

3块示范样地分别在2014年2—3月和2015年3月按照图3的补植了3个阔叶树种，补植前后林分中树种的混交度、林木的竞争关系和林木空间分布都发生了较大的变化。

补植后树种混交度较补植前有较大幅度的提高，第二次补植后树种混交度（0.191±0.007）比第一次补植后的树种混交度（0.186±0.005）有所提高，均明显大于补植前树种混交度（0.042±0.020）。因为补植前为杉木纯林，树种只有杉木与萌生的柳杉，第一次补植后树种为4种，第二次补植后树种为5种，杉木、柳杉、栾树、马褂木和观光木。经过两次补植，杉木或柳杉树种比例占63.88～66.49%，为了更好发挥生态公益林的多种功能，后期还需进行抚育间伐与阔叶树种补植，采用考虑K-阶邻近的混交方式，不同的补植树种尽可能分散分布，通过小范围的经营尽可能地提高林分的混交度。

补植后林分竞争指数有所提高，第二次补植后林分竞争指数（4.67±0.32）比第一次补植后林分的竞争指数（4.41±0.24）有提高，均大于补植前林分的竞争指数（3.92±0.20）。因为研究对象为幼龄林，补植的阔叶树种为胸径4～4.5 cm的苗木，补植后还没有完全郁闭，林木之间的竞争强度有所增强，但总体来说，林木之间的竞争强度不大。

补植后单木的平均影响范围缩小，基于Voronoi图林木所占多边形面积的变异系数减少，即林木之间影响范围的差异减小，第二次补植后基于Voronoi图的变异系数（0.48±0.07）比第一次补植后基于Voronoi图的变异系数（0.55±0.10）降低，均明显小于补植前基于Voronoi图的变异系数（2.04±0.31）。因为补植位置选择在较大的林隙处，优先补植在林隙较大的位置，结果导致林木之间距离相差较小，林木分布更加均匀。

3.5 补植前后林木与林分均质性指数

在3块示范样地内，补植后林分均质性指数比补植前有显著提高，第二次补植后林分均质性指数（1.94±0.06）比第一次补植后林分均质性指数（1.88±0.11）有提高，均大于补植前林分均质性指数（1.72±0.23）。

4 讨论与结论

4.1 结 论

长期以来，森林经营工作者优先选择“林隙地选”较大位置进行补植，但是依据确定的补植数量，考虑林木之间的竞争与混交关系，如何有序选择补植位置？本文以杉木人工纯林空间结构调控为研究目的，基于Voronoi图与Delaunay三角网进行林木补植位置与空间配置的方法研究，主要结论如下：

（1）本文借助Voronoi图和Delaunay三角网结构，为“林隙”的大小进行排序，针对不同的补植密度，能够较好地确定林木补植位置，使补植后林木的空间分布更趋于均匀分布或接近均匀分布的随机分布。本研究对象为生态公益林杉木人工纯林，通过多次的采伐与补植经营，能够达到调整与优化空间结构的目的。

（2）本文提出考虑K阶邻近林木进行补植树种的空间配置，针对补植树种的不同比例和补植林木的大小，采取单株补植方式，尽可能提高树种的空间隔离程度，补植林木数量确定后，补植树种越多，林木混交度越大。该方法通过在计算机上模拟补植林木的空间配置，选择空间结构指数和均质性指数衡量林木空间配置的效果，选择最优的空间配置方案进行林木补植，克服以前林木补植时的随机性。

（3）本文提出的林木补植位置与空间配置研究方法不仅适用于杉木人工纯林的空间结构调整与优化，也适用于其它单株补植方式，但不适合群状补植。

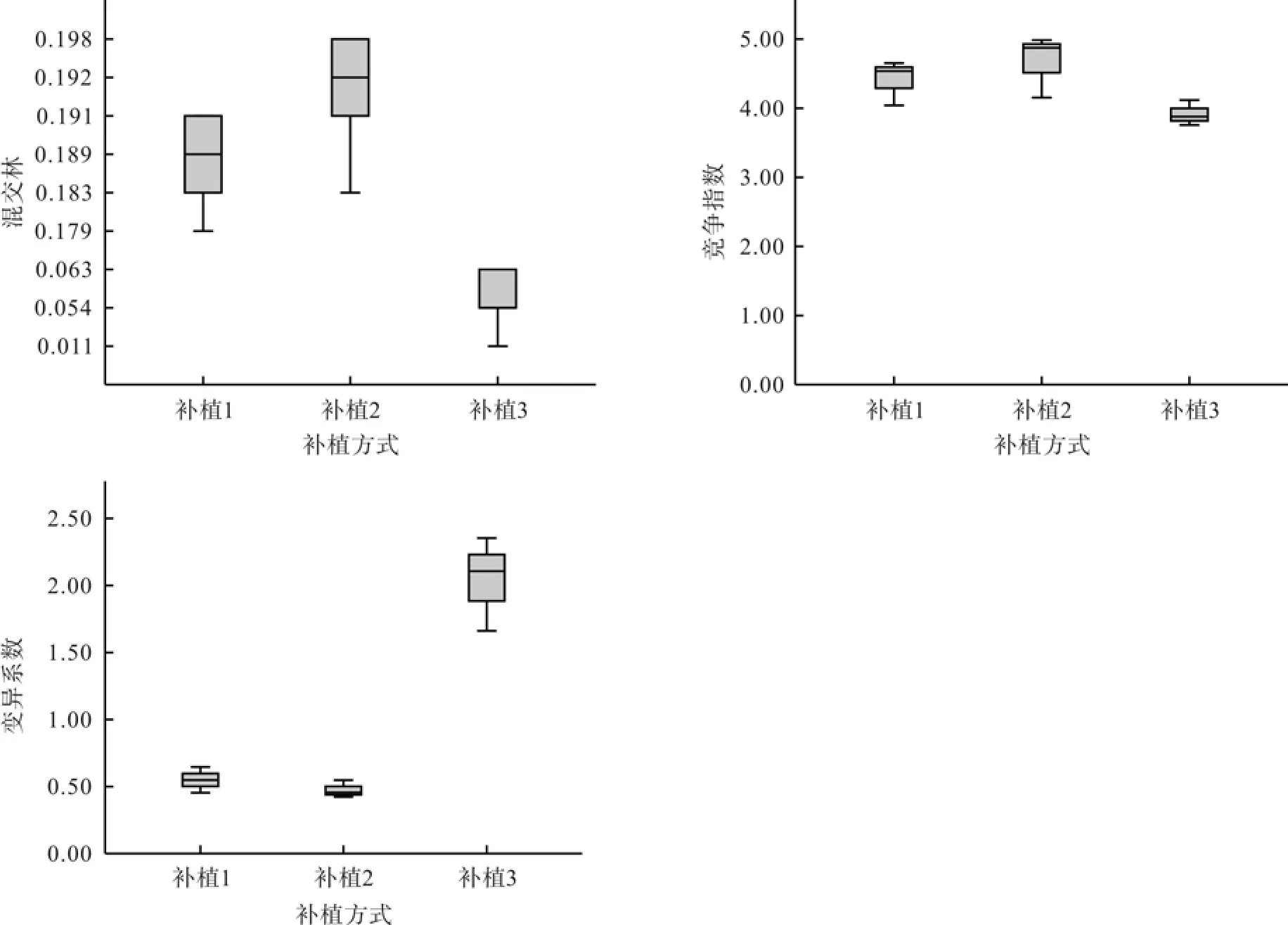
图4 两种补植方式的空间结构指数对比Fig.4 The spatial structure index of two kinds of replantations

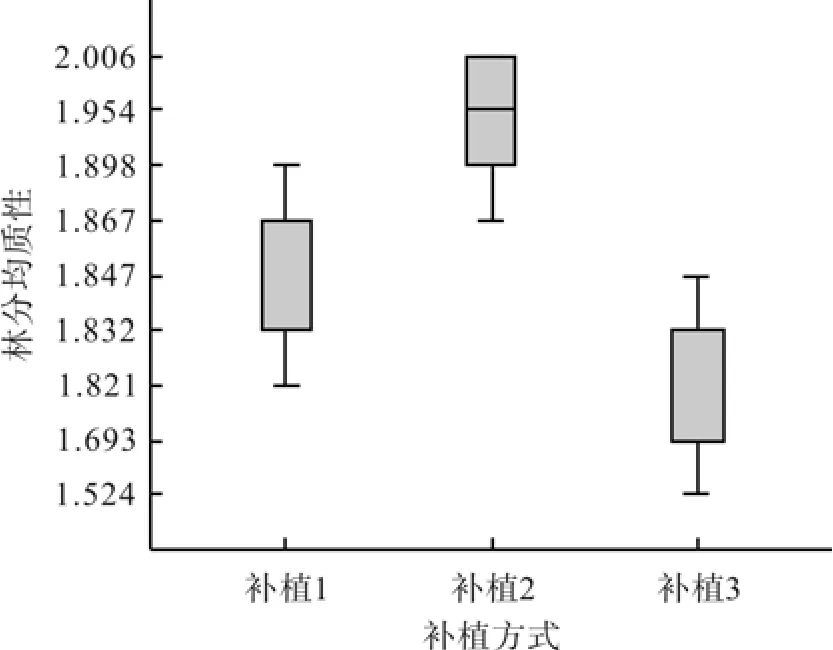
图5 两种补植方式的林分均质性对比Fig.5 The stand heterogeneity of two kinds of replantations

4.2 讨 论

本研究对象为杉木人工纯林，林木的胸径、树高和冠幅差异较小，且属于幼龄林，林木之间的竞争比较小，不同林木的竞争差异也较小，因此，本文提出补植位置选择在面积较大的Delaunay三角形内心。如果研究对象为混交林，林木个体差异较大，林木之间的竞争差异也较大，需要考虑因林木大小引起的竞争对林木补植位置的影响，这需要构建约束Delaunay三角网解决此问题。

本研究对象为杉木人工纯林，没有考虑林木的垂直结构，如果不仅考虑林分中林木树种、空间分布位置，还考虑林木的胸径、树高和冠幅，区分上层补植与林下补植，需要建立林木补植位置与空间配置模型。

[1] 谢剑斌,查 轩. 试论森林可持续经营单元的时空尺度[J]. 林业科学, 2005, 41(3): 164-170.

[2] Pommerening A. Approaches to quantifying forest structures[J].Forestry, 2002, 75(3): 305-324.

[3] North M, Chen J Q, Oakkey B,et al.Forest stand structure and pattern of old growth western Hemlock/Douglas- fir and mixedconifer forest[J]. Forest Science, 2004, 50(3): 299-311.

[4] 李建军,李际平,刘素青,等. 基于Hegyi改进模型的红树林空间结构竞争分析[J]. 中南林业科技大学学报, 2012, 30(12):23-27.

[5] 惠刚盈. 基于相邻木关系的林分空间结构参数应用研究[J].北京林业大学学报, 2013, 35(4): 1-7.

[6] 候元兆, 曾祥谓. 论多功能森林[J]. 世界林业研究, 2010,23(3): 7-12.

[7] Gadow K V, Zhang C Y, Wehenkel C,et al.Forest structure and diversity//Pukkala T, Gadow K V. Continuous cover forestry:2nd[M]. Dordrecht: Springer, 2010.

[8] Charles Duyckaerts, Gilles Godefroy. Voronoi tessellation to study the numerical density and the spatial distribution of neurons[J]. Journal of Chemical Neuroanatomy, 2000, 20: 83-92.

[9] 汤孟平, 陈永刚, 施拥军, 等. 基于Voronoi图的群落优势树种种内种间竞争[J]. 生态学报, 2007, 27(11): 4707-4715.

[10] 赵春燕,李际平,李建军. 基于Voronoi图和Delaunay三角网的林分空间结构量化分析[J]. 林业科学,2010, 46(6):78-83.

[11] 刘 帅,吴舒辞,王 红,等. 基于Voronoi图的林分空间模型及分布格局研究[J]. 生态学报, 2014, 34(6):1436-1443.

[12] 赵春燕,李际平,封 尧, 等. 考虑K阶邻近林木的混交度[J].林业科学, 2015, 51(4): 89-95.

[13] 汤孟平,唐守正,雷相东,等. 两种混交度的比较分析[J]. 林业资源管理, 2004, (4): 25-27.

[14] 赵春燕,李际平,袁晓红, 等. 泰森多边形和狄洛尼三角网的林木空间格局分析[J]. 测绘科学, 2014, 39(10): 76-80.

[15] 李建军,张会儒,刘 帅,等. 基于改进PSO的洞庭湖水源涵养林空间优化模型[J]. 生态学报, 2013, 33(13): 4031-4040.

[16] 李建军,刘 帅,张会儒,等. 洞庭湖森林生态系统空间结构均质性评价[J]. 生态学报, 2013, 33(12): 3732-3741.

[17] 黄新峰,亢新刚,杨 华, 等. 5个林木竞争指数模型的比较[J].西北农林科技大学学报: 自然科学版, 2012, 40(7):127-134.

[18] 张 宁,张怀清,林 辉, 等. 基于竞争指数的杉木林分生长可视化模拟研究[J]. 林业科学研究, 2013, 26(6):692-697.

[19] 汤孟平. 森林空间结构研究现状与发展趋势[J]. 林业科学,2013, 46(1):117-122.

[20] 王怀芳. 林分密度对30年生杉木人工林生长的影响.亚热带农业研究[J]. 2012, 8(3):156-159.

Spatial location and allocation of replanting trees on pure Chinese firplantation based on Voronoi diagram and Delaunay triangulation

ZHAO Chunyan, LI Jiping
(Central South University of Forestry &Technology, Changsha 410004, Hunan, China)

The arti ficial pure Chinese fir plantation is designated as the ecological public welfare forest. In order to improve the diversity of tree species, replanting broad-leaved trees in pure Chinese fir plantation is an effective means of multi-function management. In order to optimize the spatial structure of forest stand, this paper proposed a method of spatial location and allocation when replanting based on Voronoi graph and Delaunay triangulation. The Voronoi graph and Delaunay triangulation are constructed by the spatial position of forest individual tree as the planar dissimilarity point. K-order adjacent relationship between trees can be quantized by Voronoi graph,Delaunay triangulation include distance and the angle informations between adjacent trees, and the gap between trees. This paper only considers the horizontal spatial structure of forest stand, the variation coef ficient based on the Voronoi graph, the mingling and the competition index were chosen to describe respectively the distribution pattern, the mixed degree and the competition relationship, and the homogeneity target of spatial structure adjustment is established. Two plant initiation trees and dead trees were cut down before replanting. Two replanting tree species are respectivelyKoelreuteria paniculata,Liriodendronchinensis(Hemsl.) Sarg andMichelia odora(Chun) Noot. et B. L. Chen. The tree patch position was determined by the area size of Delaunay triangle. The spatial distribution of the trees was determined based on the K-order Adjacent, which achieved the optimization of forest stand spatial structure. The research object is the pure Chinese fir plantation, the tree species mingling of the stand before planting is very low, and it is between 0.011 and 0.063, its competition coef ficient is between 0.699 and 0.833, competitive intensity is relatively small because of the young Chinese fir and no canopy, the variation coef ficient based on Voronoi graph is between 1.662 and 2.354; The tree species mingling after replanting was improved, The mingling of the second time after replanting was greater than the first time, which was higher than before replanting.The species diversity, the mingling of tree species and the competition index were increased after replanting. The competition index of the second time after replanting is bigger than the first time, which is bigger than before replanting, which indicates that the competition strength is enhanced after replanting. The variation coef ficient based on Voronoi graph is obviously decreased. The variation coef ficient of the second time after replanting is less than the first time, which is less than before replanting. It is showed that the spatial distribution is more uniform after planting. The spatial distribution of stand can be adjusted by tree replanting based on Delaunay triangulation. The mingling of stand can be improved by tree replanting based on the K-order Adjacent, the more tree species, the more mixed degree. The tree replanting method can realize to improve the spatial structure of forest stand while optimizing the forest structure. This study can provide theoretical basis for adjustment and optimization of stand spatial structure while tree replanting, and can guide the arti ficial pure Chinese fir forest to the near natural forest, and achieve multi-function forest management.

Voronoi graph; replanting; the ecological public welfare forest; pure Chinese fir plantation; spatial structure optimization

S791.27

A

1673-923X(2017)02-0001-08

10.14067/j.cnki.1673-923x.2017.02.001

2015-08-21

“十二五”农村领域国家科技计划课题（2012BAD22B0505）；湖南省自然科学基金项目（2015JJ3175）

赵春燕，博士，副教授；E-mail： chunyan_zhao@163.com

赵春燕，李际平. 基于Voronoi图与Delaunay三角网的杉木人工纯林林木补植位置与空间配置[J].中南林业科技大学学报，2017, 37(2): 1-8.

[本文编校：吴 彬]