(2+1)维KdV方程的Bäcklund变换和无穷守恒律*

郭婷婷

(山西大学 商务学院， 山西 太原 030031)

(2+1)维KdV方程的Bäcklund变换和无穷守恒律*

郭婷婷

(山西大学 商务学院， 山西 太原 030031)

对双Bell多项式进行研究， 并基于多维双Bell多项式和标准的Hirota双线性方程之间的关系， 构造出(2+1)维KdV方程带有任意函数的双线性表达式. 运用双Bell恒等式， 确定(2+1)维KdV方程的双线性Bäcklund变换. 通过做变量变换， 将(2+1)维KdV方程的耦合系统线性化为含有多个参数的Lax对， 并证明其满足可积性条件. 此外， 求得这个非线性发展方程的无穷守恒律， 并准确地给出所有守恒密度和流量的递推公式.

双Bell多项式； (2+1)维KdV方程； Bäcklund变换； 无穷守恒律； Lax对

0 引 言

在非线性演化偏微分方程的研究中， 数学物理的科学启发性与应用数学的逻辑严密性相互渗透， 使得孤子理论在现代非线性科学中大放异彩. 而其中对孤立波的求解以及对非线性偏微分方程可积性的研究是比较重要的课题. 通过对非线性演化方程做Miura变换并引入谱参数， 可以得到波函数对时间的发展方程， 进而将偏微分方程转化为常微分方程， 从而达到对偏微分方程求解的目的. 20世纪70年代， R.Hirota给出一种有效构造演化方程精确孤波解的双线性方法[1]， 依据这种方法可以求出发展方程的单孤子、 双孤子、 三孤子解， 并推出该方程N孤子解的精确表达. 这一系列工作的前提是先确定双线性型方程. Hirota方法主要是通过对相关变量作变换， 进而求得非线性方程的双线性表示[2]， 可以运用Wronskian技巧， 结合行列式的性质， 构造偏微分方程的Wronskian行列式解和Grammian行列式解， 也可以将行列式推广为新的代数工具Pfaffian， 推导双线性方程的耦合系统以及新系统的Pfaffian解. 将传统意义上的Bäcklund变换与Hirota方法相结合， 可以求出方程的双线性Bäcklund变换、 Lax对以及无穷守恒律， 为研究方程的可积性[3]等奠定基础. 本文主要是在多维双Bell多项式的基础上， 确定(2+1)维KdV方程新的双线性表示， 其中含有任意函数φ(x)项. 这种方法不仅可以避免Hirota方法中对变量变换的选取， 也可以避免确定Bäcklund变换时对双线性恒等式的推导， 进而可以较简洁地确定方程的Lax对和无穷守恒律， 为表征非线性演化偏微分方程的可积性以及对非线性方程的求解打下基础.

1 多维双Bell多项式

多维Bell多项式定义[4]如下： 假设al≥0,l=1,2,…,k是任意整数，g=g(y1,y2,…,yk)是一个C∞多变量函数， 则

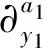
称为多维Bell多项式. 当g=g(x,y,t)时，

Bx,t(g)=gx,t+gxgt,

Bx,y(g)=gx,y+gxgy,

B3x,y(g)=g3x,y+3g2x,ygx+3gx,yg2x+

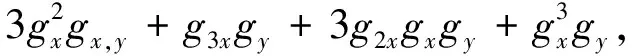
基于以上多维Bell多项式， 多维的双Bell多项式[5-6]定义如下

Pa1y1,…,akyk(n,m)=Ba1y1,…,akyk(g)|gq1y1,…,qkyk=

其中ql=0,1,…,al,l=1,…,k.

文中用到的低阶的双Bell多项式如下

Px(n)=nx,Px,y(n,m)=mx,y+nxny,

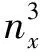
定理[7]双Bell多项式和标准的Hirota算子之间的关系如下

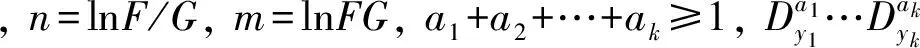
取F=G， 上式变形为

特别地，Bx,t(b)=bx,t,Bx,y(b)=bx,y,B3x,y(b)=b3x,y+3bx,yb2x.

(7)

2 (2+1)维KdV方程新的双线性表示

KdV方程是1859年由荷兰数学家科特韦格和德弗里斯共同发现的一种偏微分方程， 它在物理学的许多领域都有应用， 例如等离子体磁流波、 离子声波、 非谐振晶格振动、 低温非线性晶格声子波包的热激发、 液体气体混合物的压力表等.

非线性的(2+1)维KdV方程[2]为

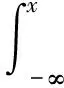
依据Hirota双线性方法作变换可以将其双线性化[2], 为避免双线性化过程中多种变换的选取， 我们将基于双Bell多项式引入位势场b， 并将方程的解表示为带有函数φ(x)的形式，

式中：φ(x)为一个可自由选取的函数. 将式(9)代入式(8)得

b2x,t+3[b2x+φ(x)]b2x,y+b4x,y+

在等式两端同时对x积分， 上式变形为

运用定理中的恒等式(6)并结合式(7)， 非线性方程可化为Bell-多项式型

结合双Bell多项式与标准的双线性算子之间的关系式(6)， 并作变量代换b=2lnF， 于是获得新的带有任意函数φ(x)的(2+1)维KdV方程的双线性表示

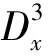
这个双线性表示与文献[9]的表达形式不同， 也是接下来确定(2+1)维KdV方程的双线Bäcklund性变换、 Lax对和无穷守恒律的前提.

3 (2+1)维KdV方程的双线性Bäcklund变换

在Hirota双线性方法中， 需要推出和选用一系列的双线性公式来确定非线性方程的双线性Bäcklund变换， 针对不同的双线性方程， 为减少相对复杂双线性公式的推导和运用， 我们将基于双Bell多项式来确定非线性方程的双线性Bäcklund变换.

首先假设a和b是变形后的(2+1)维KdV方程(11)的两个解， 于是

B(a)-B(b)=(a-b)x,t+(a-b)3x,y+

现引入两个新的变量m和n来构造限制性条件， 取

那么式(14)将改写为

B(m+n)-B(m-n)=

2nx,t+2n3x,y+6m2xnxy+6mxyn2x+6φ(x)nx,y.

依据多维双Bell多项式定义中低阶的双Bell多项式(3)， 上式可以变形为

B(m+n)-B(m-n)=

其中,

S(n,m)=

为将二场条件耦合成限制条件， 将S(n,m)表示为带有P-多项式的Wronskian形式， 即

S(n,m)=6Wronskian[Px,y(n,m),Px(n)]+

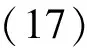
整合式(16)和式(17)得

2{∂x[Pt(n)]+

3Wronskian[Px,y(n,m),Px(n)]}+

现取

这里λ为任意常数， 于是由式(18)可以得到一个含有P-多项式的耦合系统

结合定理中的式(6)， 以上系统将化为双线性的Bäcklund变换

非线性方程双线性Bäcklund变换的获得将为方程Lax对的求解奠定基础.

4 (2+1)维KdV方程的Lax对

为将以上的耦合系统线性化， 首先利用Hopf-Cole变换

并取m=n+b. 依据定义中低阶的双多Bell项式(3)， 可得

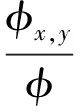
将以上各式代入双线性的Bäcklund变换式(20)中可得

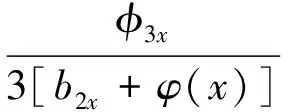
经过计算， 耦合系统式(19)～(21)将被线性化为

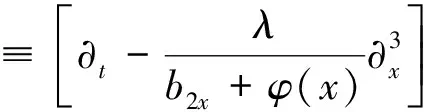
再由方程双线性表示求解中的假设式(9)， 可以得出以上Lax对的等价形式

因为u是(2+1)维KdV方程(8)的解， 容易验证以上Lax对式(28)和(29)满足可积性条件

由此可以得出， (2+1)维KdV方程(8)是可积的. 由Lax对也就容易获得(2+1)维KdV方程(8)的孤子解， Wronskian行列式解， Grammian行列式解， 并可将方程Pfaffian化[9].

5 (2+1)维KdV方程的无穷守恒律

基于双Bell多项式， 首先引入一个新的位势函数h， 并取

结合求解方程Bäcklund变换中的式(15)， 有

由方程Bäcklund变换中整合的式(18)可以得出一个Riccati型方程和一个Divergence型方程如下

注意到 ∂x[Pt(n)]=∂t[Px(n)]=nx,t， 并将式(34)代入可得

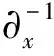
令

将其代入(37)式， 并取λ=τ3, 经过大量计算， 整理关于τ的幂次项， 可以获得守恒密度In的递推公式

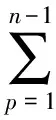
将式(39)代入式(38)， 则有

这也就给出了无穷守恒律

通过大量计算， 整合式(43)中τ的幂次项可获得连带流Fn的递推表达

6 结 论

基于多维双多Bell项式， 本文对非线性(2+1)维KdV方程进行研究， 给出(2+1)维KdV方程新的双线性表示， 其中含有任意函数项φ(x)，

在双线性型方程的基础上通过一系列计算， 确定该方程的双线性Bäcklund变换为

(Dt+3λDx)F·G=0,

(DxDy-λ)F·G=0，

Lax对为

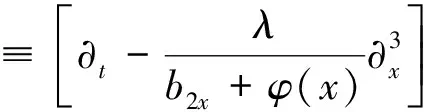
它的等价形式

以及无穷守恒律In,t+Fn,x=0,n=1,2,…， 并准确给出守恒密度的递推关系

I1=-[b2x+φ(x)]=-u,I2=-I1,x,

n=2,3,…，

以及流量的递推关系

F1=-b2x,F2=-F1,x,

n=2,3,….

这将为进一步研究非线性(2+1)维KdV方程的可积性和方程求解奠定基础.

[1] Hirota R. The direct method in soliton theory[M]. Cambridge： Cambridge University Press， 2004.

[2] Zhang Y F, Honwah T, Zhao J. Higher-dimensional KdV equations and their soliton solutions[J]. Communications in Theoretical Physics, 2006， 45(3)： 411-413.

[3] Guo F K， Feng B L， Guo T T. A few notes on Lax integrability， integrable couplings and computing formula of the constantr[J]. Journal of Applied Nonlinear Dynamics， 2012， 1(4)： 401-406.

[4] Zhang Y F, Han Y C. Some evolution hierarchies derived from self-dual Yang-mills equations[J]. Communications in Theoretical Physics, 2011， 56(5)： 856-872.

[5] Zhang Y F. Lie algebras for constructing nonlinear integrable couplings[J]. Communications in Theoretical Physics, 2011， 56(5)： 805-812.

[6] Zhang Y F， Han Y C， Mei J Q. A systematic method for solving differential difference equations[J]. Communications in Nonlinear Science and Numerical Simulation, 2010， 15(9)： 2791-2797.

[7] Guo F K, Zhang Y F. A new liouville integrable hamiltonian system[J]. Communications in Theoretical Physics, 2010， 53(5)： 809-811.

[8] 陈登远. 孤子引论[M]. 北京： 科学出版社， 2006.

[9] 郭婷婷. (2+1)维方程的孤子解和新行列式解[J]. 中北大学学报(自然科学版)， 2015， 36(2)： 118-121.

Guo Tingting. The soliton solutions and the new wronskian determinant solutions of the (2+1) dimensional KdV equation[J]. Journal of North University of China (Natural Science Edition)， 2015， 36(2)： 118-121. (in Chinese)

TheBäcklundTransformationandInfiniteConservationLawsof(2+1)DimensionalKdVEquation

GUO Ting-ting

(College of Business, Shanxi University, Taiyuan 030031, China)

The binary Bell polynomials are researched, based on the link between multi-dimensional binary Bell polynomials and the standard Hirota bilinear equation, the bilinear expressions with arbitrary function for (2+1) dimensional KdV equation are constructed, the approach is different from the Hirota bilinear method. By application of binary Bell identity, the bilinear Bäcklund transformations of the (2+1) dimensional KdV equation are obtained. By means of variate transformation, the coupled system of the (2+1) dimensional KdV equation is linearized into Lax pairs with multi-parameters, it is proved that the integrability condition is satisfied. In addition, the infinite conservation laws of this nonlinear evolution equation are derived, all conserved densities and fluxes are given with explicit recursion formulas.

binary Bell polynomials; (2+1) dimensional KdV equation; Bäcklund transformations; infinite conservation laws; Lax pairs

1673-3193(2017)03-0277-05

2016-09-21

山西大学商务学院科研基金资助项目(2016028)

郭婷婷(1983-)， 女， 讲师， 硕士， 主要从事应用数学和孤立子理论的研究.

O129.35

A

10.3969/j.issn.1673-3193.2017.03.006