Reinhardt域上的双全纯映照与Roper-Suffridge算子*
王朝君, 崔艳艳, 刘 浩, 朱思峰
(1. 周口师范学院 数学与统计学院, 河南 周口 466001; 2. 河南大学 数学与统计学院, 河南 开封 475001)
Reinhardt域上的双全纯映照与Roper-Suffridge算子*
王朝君1, 崔艳艳1, 刘 浩2, 朱思峰1
(1. 周口师范学院 数学与统计学院, 河南 周口 466001; 2. 河南大学 数学与统计学院, 河南 开封 475001)
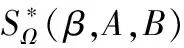
螺形映照; 星形映照; Roper-Suffridge算子
Roper-Suffridge算子在多复变函数论中占有重要的位置, 通过该算子可以由单复变中的双全纯函数构造多复变中相应的映照.目前对于该算子的研究已经取得了许多很好的结论[1-6]. 2013年夏红川[7]引入了推广的Roper-Suffridge算子
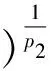
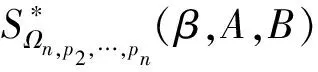
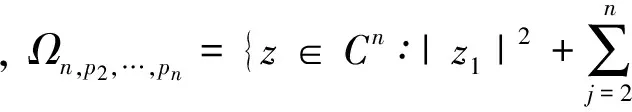
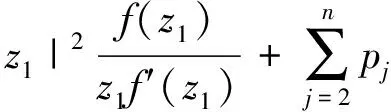
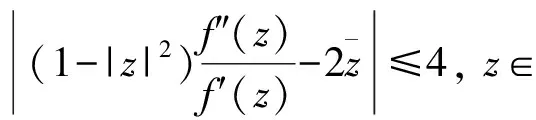
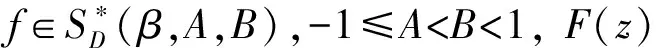
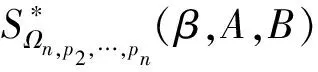
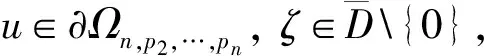
令
q(z1)=
则
且|q(z1)|<1, 由Schwarz-Pick引理[11]有
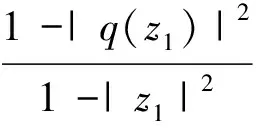
由式(3)及引理1知
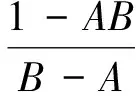
其中
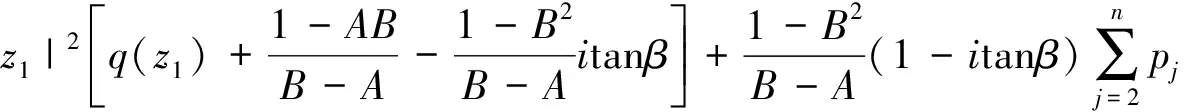
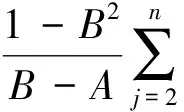
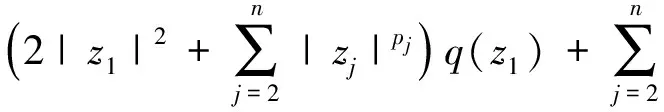
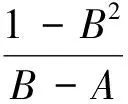
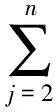
于是, 由式(4)及引理2知
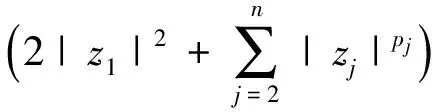
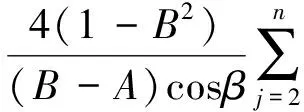
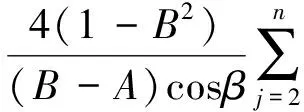
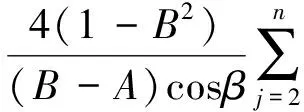
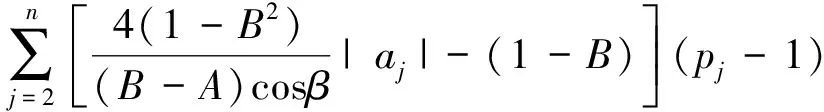
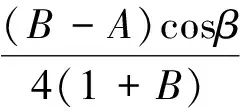
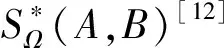
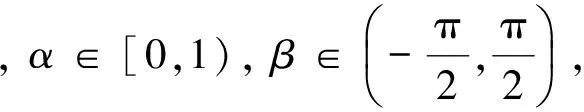
证明由强α次殆β型螺形映照的定义[13]须证
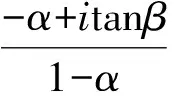
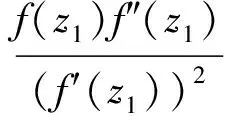
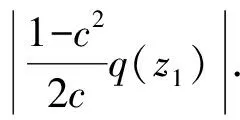
即
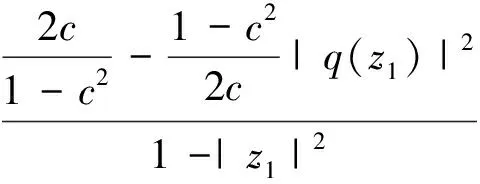
由式(6)及引理1知
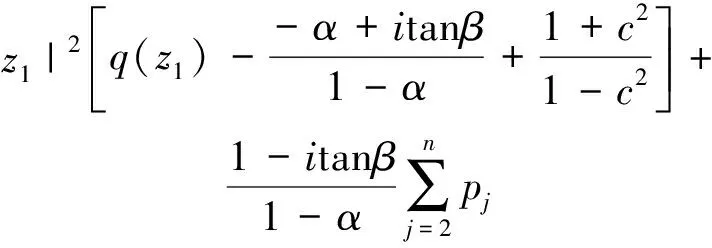
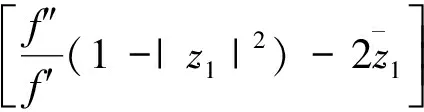
由式(7)及引理2知
|H(z)|≤
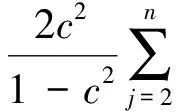
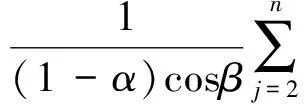
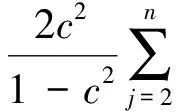
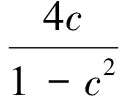
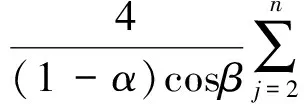
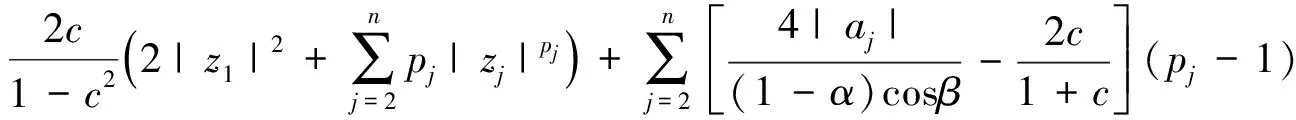
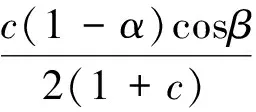
注2 在定理2中分别令α=0及β=0, 则得到相应的强β型螺形映照及强α次殆星形映照的结论, 与文献[7]的结论相一致.
[1] 冯淑霞, 刘小松, 徐庆华. Loewner链与推广的Roper-Suffridge算子[J]. 数学物理学报, 2009, 29A(6): 1601-1612.
Feng Shuxia, Liu Xiaosong, Xu Qinghua. Loewner chains and the generalized Roper-Suffridge extension operator[J]. Acta Mathematica Scientia. 2009, 29A(6): 1601-1612. (in Chinese)
[2] Liu X S, Feng S X. A remark on the generalized Roper-Suffridge extension operator for spirallike mappings of typeβand orderα[J]. Chinese Annals of Mathematics, 2009, 24(2): 310-316.
[3] 刘名生, 朱玉灿. 在Banach空间中推广的Roper-Suffridge算子(Ⅲ)[J]. 中国科学(数学), 2010, 40 (3): 265-278.
Liu Mingsheng, Zhu Yucan. The generalized Roper-Suffridge operators on Banach spaces (Ⅲ) [J]. Science China, 2010, 40(3): 265-278. (in Chinese)
[4] 刘小松, 刘太顺. Reinhardt域上和复Hilbert空间单位球上推广的Roper-Suffridge算子[J]. 数学年刊, 2005, 26A(5): 721-730.
Liu Xiaosong, Liu Taishun. The generalized Roper-Suffridge extension operator on a Reinhardt domain and the unit ball in a complex Hilbert space[J]. Annals of Mathematics, 2005, 26A(5): 721-730. (in Chinese)
[5] 崔艳艳, 王朝君. Reinhardt域上推广的Roper-Suffridge算子与Loewner链[J]. 中北大学学报(自然科学版), 2014, 35(4): 376-379.
Cui Yanyan, Wang Chaojun. The generalized Roper-Suffridge extension operator on Reinhardt domains and Loewner chains[J]. Journal of North University of China (Natural Science Edition), 2014, 35(4): 376-379. (in Chinese)
[6] Li H J, Feng S X. Roper-Suffridge extension operator on a Reinhardt domain[J]. Acta Mathematica Scientia, 2014, 34B(6): 1761-1774.
[7] 夏红川. 有关全纯映照子族的两类Roper-Suffridge算子[D]. 开封: 河南大学, 2013.
[8] Wang J F, Gao C L. A new Roper-Suffridge extension operator on a Reinhardt domain[J]. Abstract and Applied Analysis, 2011(2): 249-265.
[9] Muir J R. A class of Loewner chain preserving extension operators[J]. Journal of Mathematical Analysis & Applications, 2008, 337(1): 862-879.
[10] Wang J F. Modified Roper-Suffridge operator for some subclasses of starlike mappings on Reinhardt domains[J]. Acta Mathematica Scientia, 2013, 33B(6): 1627-1638.
[11] Ahlfors L V. Complex analysis[M]. New York: McGraw-Hill, 1953.
[12] 王建飞. Cn中一类星形映射子族的增长定理及推广的Roper-Suffridge算子[J]. 数学年刊, 2013, 34A(2): 223-234.
Wang Jianfei. On the growth theorem and the Roper-Suffridge extension operator for a class of starlike mappings in Cn[J]. Annals of Mathematics, 2013, 34A(2): 223-234. (in Chinese)
[13] 蔡荣华, 刘小松. 强螺形函数子族的第三项和第四项系数估计[J]. 湛江师范学院学报, 2010, 31(6): 38-43.
Cai Ronghua, Liu Xiaosong. The third and fourth coefficient estimations for the subclasses of strongly spirallike functions[J]. Journal of Zhanjiang Normal College, 2010, 31(6): 38-43. (in Chinese)
BiholomorphicMappingsonReinhardtDomainsandGeneralizedRoper-SuffridgeOperators
WANG Chao-jun1, CUI Yan-yan1, LIU Hao2, ZHU Si-feng1
(1. School of Mathematics and Statistics, Zhoukou Normal University, Zhoukou 466001, China; 2. School of Mathematics and Statistics, Henan University, Kaifeng 475001, China)
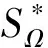
spirallike mappings; starlike mappings; Roper-Suffridge operator
1673-3193(2017)03-0273-04
2016-08-30
国家自然科学基金资助项目(11271359, U1204618); 河南省教育厅科学技术研究重点资助项目(14B110016); 河南省科技厅科技发展计划资助项目(102400450003)
王朝君(1981-), 男, 讲师, 硕士, 主要从事多复变函数论, 微分方程的研究.
O174.56
A
10.3969/j.issn.1673-3193.2017.03.005

