官坝河泥石流含沙量变化过程数值模拟

李俊， 陈宁生， 赵苑迪

(1.四川理工学院土木工程学院， 四川自贡643000；2.中国科学院大学水利部成都山地灾害与环境研究所， 成都610041)

官坝河泥石流含沙量变化过程数值模拟

李俊1， 陈宁生2， 赵苑迪1

(1.四川理工学院土木工程学院， 四川自贡643000；2.中国科学院大学水利部成都山地灾害与环境研究所， 成都610041)

泥石流输沙规律是科学布置泥石流防治工程的基础。基于Euler模型模拟了1998年7月6日官坝河泥石流含沙量变化过程。研究结果有两点：(1)泥石流输沙运动中含沙量大小和沟道宽度成正比关系。(2)泥石流在沟道地形较陡的地区携带泥沙能力强，在地形较缓的地区携带泥沙能力较弱。研究成果有助于科学布置官坝河泥石流防治工程，也为解决邛海泥沙淤积问题提供更多的科学依据。

西昌市官坝河；泥石流；输沙过程；Euler方程

引言

对于大部分泥石流沟，已发生的泥石流相关参数是确定该沟泥石流治理工程设计值的重要依据[1-3]。比如已发生的泥石流容重、流速、流量和输沙量是泥石流拦沙坝和排导槽的重要设计依据。所以在泥石流工程防治中，泥石流工作者的首要任务是调查某泥石流沟的历史泥石流发生时间，规模大小，泥石流性质和输沙规律等[4-9]。本文以邛海官坝河近100年来最大规模的泥石流为例(即1998年7月6日官坝河泥石流)，模拟该次泥石流输沙过程，总结该次泥石流输沙规律，为官坝河泥石流工程布置提供科学依据，以期通过官坝河泥石流治理工程减少邛海泥沙淤积量。

四川省西昌市的邛海为第四纪构造断陷淡水湖盆，呈北北西向不规则长方形展布，湖盆面积27 km2。其中流域面积为137.24 km2的官坝河为汇入邛海水系中汇水面积最大的支流。据实地调查，1998年7月6日官坝河发生特大型泥石流，泥石流输移的泥沙一次性把邛海海岸线推进了172 m，入海淤积量为68.98×104m3，推进淤积面积为0.089 km2，为近百年邛海流域内最大规模的泥石流[10-11]。该次泥石流导致人们赖于发展的邛海明珠“光泽”逐渐暗淡[12-13]。为减少官坝河泥石流携带的泥沙进入邛海，本文通过Euler数值模拟方法研究1998年7月6日官坝河泥石流的输沙过程，为官坝河泥石流工程布置提供科学依据，也为彻底解决邛海的泥沙淤积问题奠定科学基础。

1 模拟原理与方法

根据钱宁团队的研究成果[14-16]，泥石流可视为固液两相流。因而Euler方法适合于模拟1998年7月6日官坝河泥石流输沙过程。通过实地调查，获取主沟(巴拉拉窝段)上游300 m处洪痕断面，并得出该处洪痕断面处泥石流洪峰流量。采用Euler模型模拟泥石流含沙量的变化过程，得出该段的泥沙体积分数等场量，根据实际沟道泥石流堆积情况验证模拟结果的正确性，最后分析该段沟道泥石流输沙过程。在确定泥石流水面线方面，Euler方法的计算精度低。为了解决这一问题，本文尝试用计算自由水面线精度较高的VOF方法确定泥石流浆体的自由水面线，再根据Euler方法模拟泥石流含沙量的变化过程。利用RNGk-w紊流模型模拟泥石流的运动规律，并将泥石流视为具有一定粘度的浆体，即二相流中的液相。这样即可用VOF得到泥石流浆体与空气间的自由水面线。该水面线计算精度高且与实际调查结果相符。在此基础上，把自由水面线加在已建模型里，形成封闭的有压流，再用Euler方法确定泥石流含沙量的变化过程。技术路线如图1所示。

图1研究技术路线

在模拟软件中建立官坝河局部河流段数值模型，采用VOF跟踪计算官坝河局部河流段泥石流浆体的自由水面，将自由水面线加入已建立的官坝河局部河流段数值模型，从而建立固液两相流的Euler数值模型，最后根据拉格朗日计算方法，在多重参考系坐标下，选用标准k-ε模型，对官坝河局部段泥石流输沙过程进行数值模拟。

2 模拟方程

2.1VOF气液两相流模型

连续方程：

(1)

动量方程：

(2)

k方程：

Gk-ρε

(3)

ε方程：

(4)

式中：ρ为液体体积平均的密度，μ为分子粘性系数，μt为紊流粘性系数，P为修正的压力，Gk为由平均速度梯度引起的紊动能产生项。

2.2Euler多相流模型

欧拉多相流模型是将颗粒相作为拟流体，认为颗粒与流体是共同存在且相互渗透的连续介质，并一同在Euler坐标系下处理，为连续流体模型。其模型包括3个重要部分：场方程、构造方程和界面条件的推导。场方程遵循动量、质量、能量守恒原理。描述固液两相流的连续方程为：

(5)

式中：α1为液体体积分数，v1为液相流速，ρ1为液相的物理密度，ms1为固相与液相间的质量传递分数。

欧拉多相流模型规定，体积分数代表了每相所占据的空间，并且每相独自的满足质量和动量守恒定律，各项体积分数之和为1。

3 模型建立及条件给定

3.1 主沟(巴拉拉窝段)上游300 m沟道模型建立

数值模拟的基础资料为巴拉拉窝上游300 m沟道的地形图(图2)，该位置的经纬度为N27°48′59.37" E102°26′9.93″，建立该段的模型网格图，并根据VOF方法模拟得出该段的自由水面图(图3)。

图2巴拉拉窝上游300 m沟道地形图

图3巴拉拉窝上游300 m附近模型

该模型总长度为80 m，泥石流自由水面变化幅度为1.5 m～4 m。根据实地调查，该段泥石流容重为1.77 g/m3。泥石流浆体含有大量的水沙混合物，平均粒径为10 mm，细颗粒含量为5%，整体泥石流流动状态为连续流。

为保证数值模拟的来流条件与实际情况相吻合，模型的网格间距为1 m。在兼顾计算机的计算能力下，计算区域网格以结构化网格为主，总的计算单元约为10.5万。模型进水口泥石流最高水位高程为2340 m，泥石流流量为74.18 m3/s。

3.2 主沟(巴拉拉窝段)上游300 m沟道初始条件和边界条件

VOF模型中泥石流浆体流量为2700 m3/s，气相采用天然空气，液相和气相体积分数之和为1。计算泥石流粘滞系数η：

(6)

其中，rc为泥石流容重，为1.77 g/cm3。计算得泥石流浆体的粘滞系数为0.12 kg/(m·s)。

VOF模型中，气相作为主相，液相作为次相。在巴拉拉窝上游300 m沟道模型进口处采用流速控制模拟精度，液相流速为6 m/s，粘滞系数为0.12 kg/(m·s)。出口处采用大气压力控制模拟精度。沟床和沟坡采用无滑移边界条件。模型上方与空气接触的表面设为开敞边界。对于无滑移边界，各点输沙率均取为0。需要指出的是该模型未考虑泥石流侧蚀和下蚀作用。

Euler模型中，固相为大于2 mm的泥石流浆体。液相为小于2 mm的泥石流浆体，即为泥沙，其流量为2700 m3/s，粘滞系数为0.12 kg/(m·s)，固相作为主相，液相作为次相，液相和固相体积分数之和为1。在模型进口处采用流速控制模拟精度，液相流速为5.5 m/s。出口处采用大气压力控制模拟精度。沟床和沟坡采用固定边界。沟顶采用大气压力控制。对于固定边界，各点输沙率均取为0。

4 模拟结果验证

根据Euler方法计算得出X=5 m和X=75 m处泥沙体积分数(图4和图5)，图4中，X=5.5 m，Z=2234.5 m处的泥沙体积分数为0.6。而在表1中，泥石流在相应位置的颗粒百分含量为0.54，与计算相比小了0.06，这是因为调查时间(2010年)距离1998年相差了12年，在这些年中，雨水不断下渗，带走了部分泥沙颗粒。所以实地调查的泥沙比计算得出的泥沙体积分数少。在相应的深度范围内，实地调查的泥沙比Euler方法计算得出的泥沙体积分数相差较小，说明Euler计算结果是与实际情况较吻合。图5中，在Z=2.5 m深度范围内，实地调查的泥沙比Euler方法计算得出的泥沙体积分数相差较小，这说明了Euler公式计算得出泥沙体积分数较为准确，并且表明这种方法计算泥石流运动过程是可行的。通过以上分析，可以采用Euler方法计算分析官坝河局部段泥石流输沙过程的变化规律，为研究官坝河泥石流输沙机制奠定基础。

图4X=5.5 m时泥石流浆体与泥沙体积分数分布图

图5X=75 m时泥石流浆体与泥沙体积分数分布图

取样位置颗粒百分含量沿深度分布(单位：m)005115225X=5m001004017023054/X=75m001001009015020055

5 主沟(巴拉拉窝段)上游300 m处泥石流输沙过程分析

泥石流浆体和泥沙体积分数的横向变化如图6、图7所示。

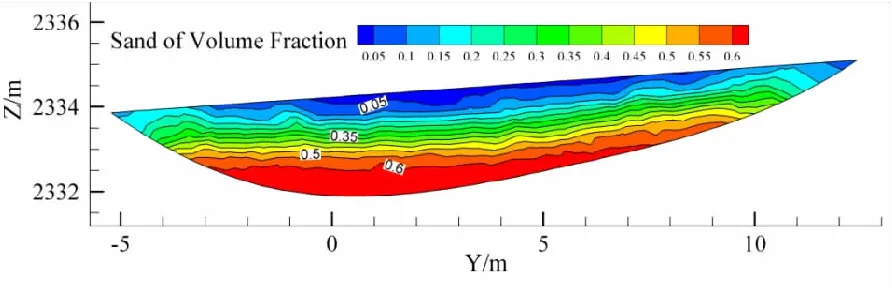
图6X=15 m时泥石流浆体与泥沙体积分数分布图

图7X=55m时泥石流浆体与泥沙体积分数分布图

由图6、图7可知，泥沙体积分数在沟底均为0.6%。说明泥石流中泥沙运动主要集中于泥石流流体中下部，有利于泥沙沉积。另外泥沙在地形较缓的地方体积分数主要聚集在下部，如图6所示，聚集深度为0.5 m～1.2 m之间。泥沙在地形较陡的地方体积分数主要聚集在中下部，如图7所示，聚集深度为1.5 m～2.3 m之间，这说明泥石流在沟道地形较陡的地区携带泥沙能力强，在地形较缓的地区携带泥沙能力较弱，此现象符合泥石流的侵蚀规律。

通过tecplot软件得出各个断面的输沙量百分数，绘制该段泥石流输沙量变化图(图8)。

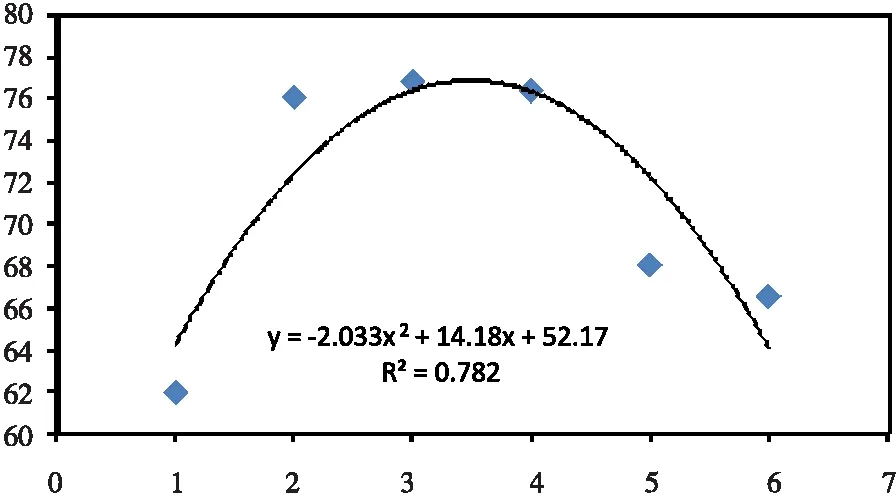
图8官坝河泥石流输沙量变化过程

在不考虑山坡两侧泥石流侧蚀和沟底泥石流侵蚀作用所搬运的泥沙情况下，泥石流含沙量从断面1-6的大小先增加后减小，含沙量在断面3处达到最大值，为76%。而断面1-6的沟道宽度分别为18 m，25 m，28 m，31 m，20 m，19 m。沟道宽度也是先增加后减小的曲线。因而含沙量的大小与沟道宽度成正比关系。

6 结束语

研究结果表明，Euler数值模拟方法能够较好地模拟官坝河局部沟道泥石流的泥沙分布范围和体积分数等水力参数。通过Euler法获得的泥沙体积分数和泥沙分布范围，结合实际沟道的泥沙分布范围和泥石流动力学参数，发现该沟的泥沙运动规律有两点。(1)官坝河局部沟道泥石流输沙运动中含沙量大小和沟道宽度成正比关系。(2)泥石流在沟道地形较陡的地区携带泥沙能力强，在地形较缓的地区携带泥沙能力较弱。值得说明的是，因该沟道模型较小，可在小流域内直接建立Euler计算模型且精度较高。在中大流域里，由于软件限制和计算机性能限制，不能建立整个沟道的Euler计算模型，这时可采用分段建立模型的方法，分别计算泥石流输沙过程中泥沙体积分数和泥沙分布范围，得出单个模型的输沙量，最后把各个模型的输沙量累加得出整个流域的输沙量。

[1] 齐宪阳,陈宁生,李俊,等.新疆阿合奇县牙尔巴西沟泥石流特征与防治[J].人民长江,2016,47(2):23-26.

[2] 崔鹏,庄建琦,陈兴长,等.汶川地震区震后泥石流活动特征与防治对策[J].四川大学学报:工程科学版,2010,42(5):10-19.

[3] 胡凯衡,葛永刚,崔鹏,等.对甘肃舟曲特大泥石流灾害的初步认识[J].山地学报,2010,28(5):628-634.

[4] 陈宁生,崔鹏,刘中港,等.基于黏土颗粒含量的泥石流容重计算[J].中国科学,2003,33(S1):164-174.

[5] 胡桂胜,陈宁生,赵春瑶,等.长江上游梯级电站开发区泥石流的治理工程效果评估与减灾策略—以金沙江白鹤滩水电站为例[J].水土保持通报,2017,37(1):241-247.

[6] 李俊,陈宁生,欧阳朝军,等.扎木弄沟滑坡型泥石流物源及堵河溃坝可能性分析[J].灾害学,2017,32(1):80-84.

[7] 王怡璇,朱利东,杨文光,等.汶川地震与芦山地震次生地质灾害特征对比[J].四川理工学院学报:自然科学版,2015,28(2):63-68.

[8] 舒志乐,史宝宁,张德宇.色多沟泥石流动力特征及危险性评估研究[J].四川理工学院学报:自然科学版,2016,29(6):70-74.

[9] 吴佳晔.日本东北大地震对我们的警示[J].四川理工学院学报:自然科学版,2011,24(2):125-128.

[10] CHEN N,CHEN M,LI J,et al.Effects of human activity on erosion,sedimentation and debris flow activity-A case study of the Qionghai Lake watershed,southeastern Tibetan Plateau,China[J].Holocene,2015,25(6):973-988.

[11] WEI X L,CHEN N S,CHENG Q G,et al.Long-term Activity of Earthquake-induced Landslides:A Case Study from Qionghai Lake basin,Southwest of China[J].Journal of Mountain Science,2014,11(3):607-624.

[12] 李俊,陈宁生.官坝河泥石流动力学特征参数[J].水土保持研究,2013,20(1):264-268.

[13] 余斌,王士革,章书成,等.鹅掌河泥石流对四川邛海影响的初步研究[J].湖泊科学,2006,18(1):57-62.

[14] 王兆印.河流动力学与河流综合管理[M].北京:清华大学出版社,2014.

[15] 钱宁,王兆印.泥石流运动机理的初步探讨[J].地理学报,1984,39(1):33-43.

[16] WANG Z Y,QI L J,WANG X Z.A prototype experiment of debris flow control with energy dissipation structures[J].Natural Hazards,2012,60(3):971-989.

Simulation of the Change Process of Sediment Concentration of Debris Flow in the Guanbariver

LIJun1,CHENNingsheng2,ZHAOYuandi1

(1.School of Civil Engineering,Sichuan University of Science & Engineering, Zigong 643000,China; 2.Institute of Mountain Hazards and Environment,CAS,Chengdu 610041,China)

The change process of sediment concentration is the basis for arranging debris flow prevention and control project scientifically.The sediment concentration cannot be obtained from field investigation.Therefore,using simulation method of Euler model,the process of sediment concentration of debris flow in Guanbariver on July 6th1998 is simulated.The resultsare shown as follows.Firstly,sediment concentration of debris flow is proportional to valley width in Guangbariver.Secondly,the debris flow has strong carrying capacity of sediment in areas with steep topography,and has less carrying capacity of sediment in areas with slower topography.The research results are helpful to the scientific arrangement of debris flow prevention project in Guanbariver,and also solve the problem of sediment deposition in Qionghai Lake.

Guanbariver; debris flow; sediment concentration; Euler model

1673-1549(2017)06-0071-05

10.11863/j.suse.2017.06.13

2017-09-12

国家自然科学基金(41661134012)；四川省安全生产科技项目(aj20170601105926)

李 俊(1989-)，男，四川乐山人，讲师，博士，主要从事山地灾害形成机理及其防治技术方面的研究，(E-mail)lijunxiaoyouxiang@163.com

X43

A