无人机对风切变干扰的BSSA控制器的设计

徐建勋

(四川理工学院自动化与信息工程学院， 四川自贡643000)

无人机对风切变干扰的BSSA控制器的设计

徐建勋

(四川理工学院自动化与信息工程学院， 四川自贡643000)

为了克服四旋翼无人直升机在飞行过程中受到风切变干扰而不稳定的问题，设计出了反步滑模自适应控制器。首先建立无人机在风切变中的动力学模型，之后将反步自适应控制与滑模控制方法结合，推导并设计出反步滑模自适应控制器，最后在Simulink中进行仿真实验。实验结果表明，在风切变的作用下反步滑模自适应控制器(BSSA)与反步自适应控制器(BSA)相比，反步滑模自适应控制器能够进一步缓解风切变对无人机造成的影响，具有更强的鲁棒性。

风切变；无人机；反步自适应控制；滑模控制

引言

四旋翼无人直升机的控制系统是一个欠驱动、强耦合的非线性系统，而且在无人机的控制系统中存在因飞行环境具有很大的差异而造成的不确定参数，这使得无人机的稳定性控制问题成为了一个难点。因此对无人机稳定性进行准确控制的方法研究成为不少科研人员研究的课题[1]。

风切变作为低空中常见的一种风场，情况复杂多变，有水平方向上的水平切变，水平方向上的垂直切变等多种形式。研究人员通过多年研究发现水平方向上的风切变对飞行器的飞行具有很大的影响[2-3]。针对右侧水平风切变的对无人机的干扰问题，吴华采用滑模控制算法能够有效抑制扰动对飞行稳定的影响[4]，但是风切变的干扰时间太短，而且在干扰期间对位移和姿态的输出没有约束。文献[5]设计的自抗扰控制能够保证在风切变的影响下，四旋翼无人机仍能够稳定飞行，但是建立的数学模型只考虑了风速对两个旋翼产生了影响，没有考虑风切变是否对无人机的输出位移的影响。

本文在文献[4]的基础上进一步考虑右侧风切变对四旋翼无人机飞行时的稳定性控制研究。根据贝兹定理得出风切变对无人机旋翼的影响，并建立在风切变影响下的无人机的数学模型；之后将反步自适应控制算法与滑模控制相结合设计出反步滑模自适应控制器，并在Matlab中对所提出来的控制算法的控制性能进行验证。

1 四旋翼无人机的动力学模型

四旋翼无人直升机是由机体与四个旋翼组成的飞行器，其结构如图1所示，其中四个旋翼由于高速旋转而产生的升力是无人机的主要动力来源，它能够使四旋翼无人直升机做出悬停，垂直上升或下降、俯仰、滚转和偏航等多种运动方式。

在建立四旋翼无人直升机的动力学方程之前，必需先定义所需要的地面坐标系和机体坐标系，如图2所示。

图1四旋翼无人直升机结构模型

图2地面坐标系与机体坐标系

在忽略弹性形变及振动的前提下，四旋翼无人直升机的飞行运动可以近似地认为是六个自由度的刚体运动，即绕三个轴的转动和沿三个轴的线运动。针对此种情况，可以利用牛顿-欧拉方程来构造相应的平衡方程式[6]：

(1)

其中：x,y,z为飞行器的位置向量；φ、θ、Ψ分别为滚转角、俯仰角以及偏航角；m是四旋翼无人直升机的质量；g是重力加速度；Ix,Iy,Iz,Ixz均为转动惯量；L是无人机的四个旋翼到机体中心的距离；U1,U2,U3,U4均是无人机系统的控制输入量，其大小分别为[7]：

(2)

其中：b是比例常数；ω为旋翼的转速；D为旋翼在空气中的阻力系数。

2 风干扰下无人机的动力学模型

根据风切变事故分析统计数据，FAA(美国联邦航空航空局)给出了四种用于飞行模拟的风切变模型，其中，3号风切变模型与现实中造成飞行器飞行事故的风切变很相似，它是一个含有水平漩涡的三维微下冲气流模型，很适合用于模拟飞行器飞行训练的风切变大气环境[8]。更重要的一点是，3号风切变模型不与风系数共同使用，因此适用于所有飞机。图3给出了3号风切变模型。

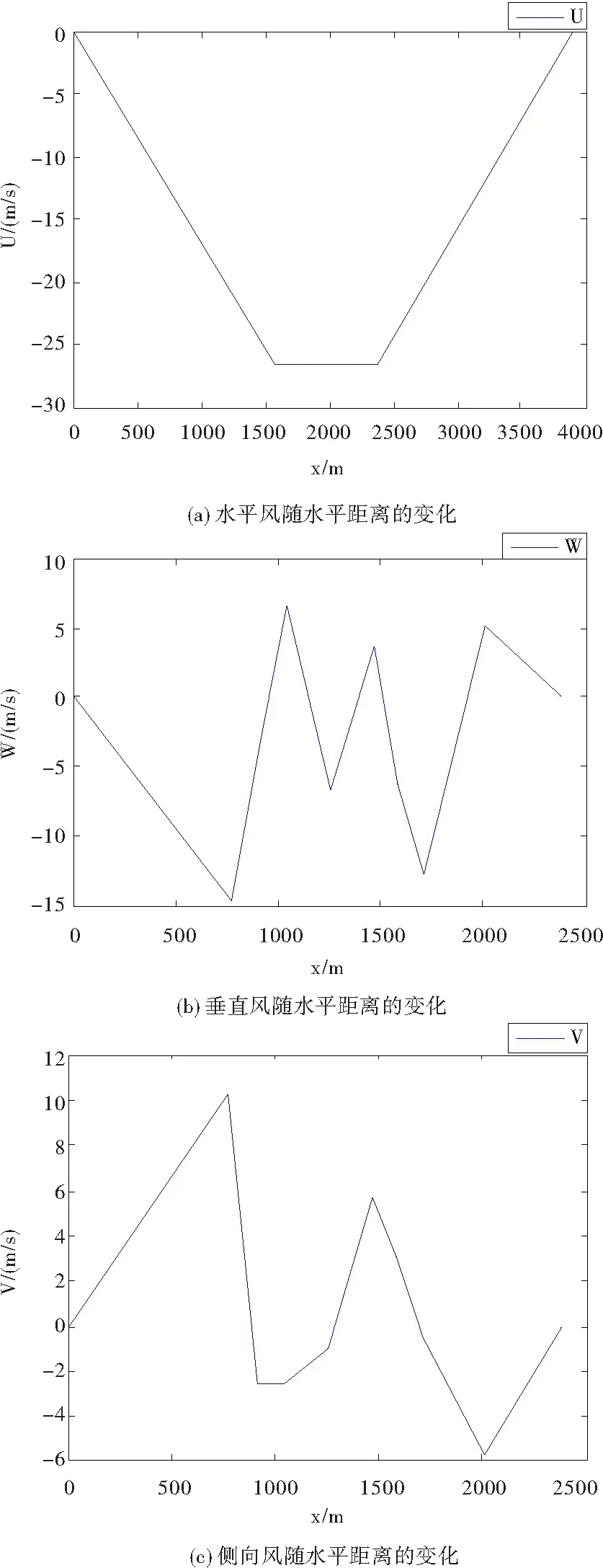
图33号风切变模型

为了便于分析右侧风切变对无人机的影响，同时为了分清左侧向风与右侧向风对无人机影响的差异，在本文中假设风速对无人机的影响主要包括旋翼，并且其影响与无人机的姿态角无关。其中风速只对1、2、3号旋翼产生干扰影响。此时，无人机的动力学模型转换为：

(3)

其中：Si(i=1,2,3,4)是气流对四旋翼无人直升机的四个旋翼的升力，S4=0。由贝兹理论[9]可以得出气流对旋转的旋翼产生的升力为：

(4)

其中：ρ为空气密度；Ad为旋翼圆盘的截面面积；V1为风速大小；a为轴流诱导因数，一般取值为0.5。

3 反步滑模自适应控制器设计

在对四旋翼无人直升机的控制系统进行设计时，可以将无人机的整个控制系统分解为两个子控制系统，即姿态子控制系统和位置子控制系统[10-14]，如图4所示。将式(3)写成状态空间表达式的形式：

(5)

其中xi(i=1,2,…,12)是状态向量：

(6)

图4无人机控制系统结构图

3.1 姿态子控制系统

以滚转角为参考来说明姿态控制器的设计:

步骤1假设四旋翼无人直升机的期望滚转角x1d与实际的滚转角之间的误差为：

Z1=x1d-x1

(7)

根据Lyapunov理论，当滚转子系统在Z1=0时处于平衡状态，可以选定Lyapunov函数：

(8)

对其求导得：

(9)

(10)

(11)

步骤2假设四悬翼无人直升机的滚转角速度的跟踪误差为：

(12)

取Lyapunvo函数，使其为：

(13)

其中：S为需要设计的滑模面；Δd是实际的不确定项d1与不确定项的估计值的差异，即估计误差：

(14)

设计滑模面S为：

S=a1Z1+Z2

(15)

其中：a1为可调参数。

步骤3设计滑模趋近律，使其满足指数趋近率[15-16]：

(16)

结合上面所给的一些式子，可以求出：

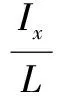
(17)

(18)

类似地，可以推断出俯仰子控制系统、偏航子控制系统的控制量及其不确定项的估计值：

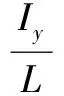
(19)

(20)

(21)

(22)

3.2 位移子控制系统

与姿态子控制系统类似，可以推出位移子控制系统中相应的控制量与不确定项的估计值：

(23)

(24)

(25)

(26)

4 仿真验算

为了验证该算法是否能有效地保证无人机在风切变的干扰下能够稳定地飞行，进行了两个不同的数值仿真实验。表1～表3分别给出了无人机动力学模型中的相关系数、反步自适应控制器(BSA)的控制参数、反步滑模自适应控制器(BSSA)与的控制参数。

表1无人机动力学模型中的相关系数

表2反步自适应控制器(BSA)的控制参数

表3反步自适应控制器(BSA)的控制参数

4.1 定点悬停

假设四旋翼无人直升机的初始位置为(0,0,0)，在[5,15] s内受到类似图3中侧向风切变的风速是V=4+0.0135x的右侧风。系统的仿真时间T=40 s，图5～图11给出了仿真实验结果。

图5无人机x位移输出

图6无人机y位移输出

图7无人机z位移输出

图8无人机Φ姿态角输出

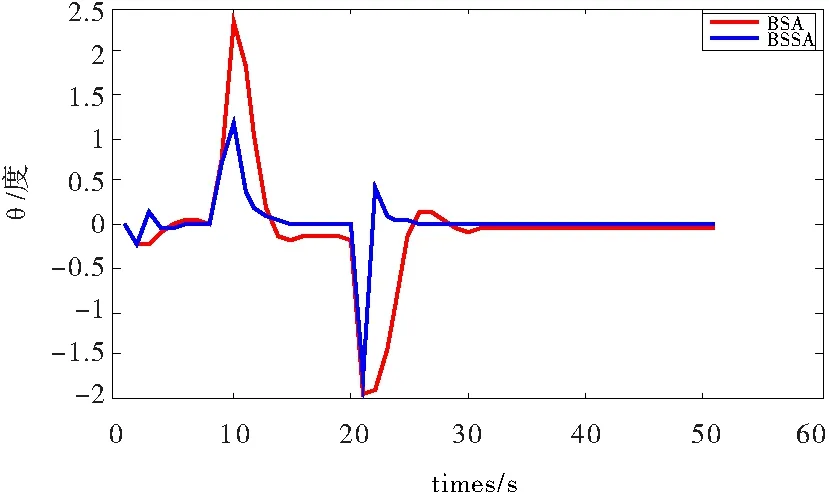
图9无人机θ姿态角输出

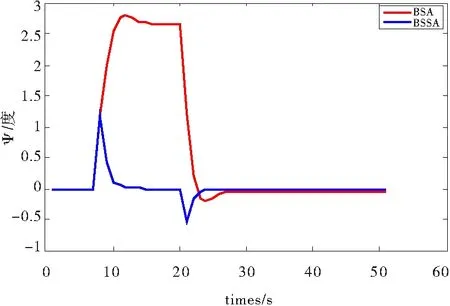
图10无人机Ψ姿态角输出

图11无人机三维飞行路径

从图5～图10可以看出，干扰消失后，反步自适应和反步滑模自适应控制方法均能使无人机的输出稳定。其中，无人机的水平方向的位置输出能够稳定地跟踪目标位置，而在干扰消失后的一小段时间后垂直方向上的位置输出也达到稳定。在风切变干扰期间，反步滑模自适应控制算法能够进一步缓解无人机的姿态角变化的时间与幅度。

4.2 轨迹跟踪

假设四旋翼无人直升机的初始位置为(0,0，0)处，并且其初始姿态角为(0,0,0)度，而无人机的目标位置为(cos(t),sin(t),1)，目标偏航角为0度。在时间T=[5，15] s内仍然有风切变干扰存在，系统的仿真时间T=40 s，控制器中的参数设置与定点悬停实验的参数一致，图12～图15给出了Simulink仿真的结果。

图12无人机x位移输出

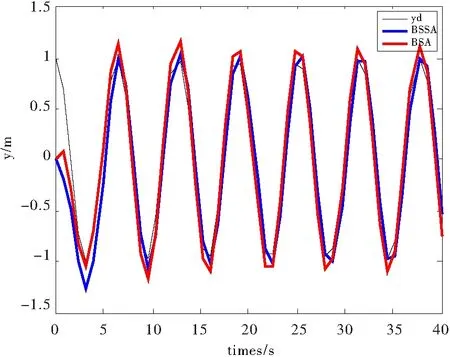
图13无人机y位移输出

图14无人机z位移输出

图15无人机Ψ姿态角输出

从仿真图可以看出，在整个仿真过程中，反步自适应控制算法与反步滑模自适应控制算法都可以跟踪预期目标路径，但是反步滑模自适应控制算法的拟合精度更高，而且在一定程度上缓解了无人机的输出的抖动。

由以上两个仿真实验可以得出：

(1) 风切变对四旋翼无人直升机的飞行品质具有很大的影响力。

(2) 在风切变作用下，反步滑模自适应控制算法具有良好的鲁棒性。

5 结束语

为了实现无人机能够在风切变中稳定飞行，本文首先给出了在风切变中的无人机的六自由度模型，其次，将反步自适应控制算法与滑模控制相结合，得到了反步滑模自适应控制算法，最后通过定点悬停和轨迹跟踪这两个实验验证出在风切变的干扰下，反步滑模自适应控制算法具有更强的鲁棒性。

[1] SHARIFI M,SAYYAADI H.Nonlinear robust adaptive Cartesian impedance control of UAVs equipped with a robot manipulator[J].Advanced Robotics,2015,29(3):171-186.

[2] HILL D J,SAFFMAN P G.Counter-Rotating vortex patches in shear: a model of the effect of wind shear on aircraft trailing vortices[J].Proceedings Mathematical Physical & Engineering Sciences,2002,458(2023):1527-1553.

[3] 金长江,张洪.低空风切变危险尺度研究[J].航空学报,1992,13(10):481-486.

[4] 吴华,宋自立,李国栋,等.电力巡检飞行机器人抗风控制器设计[J].华中科技大学学报:自然科学版,2013,41(s1):443-446.

[5] 冯长辉,齐晓慧,苏立军,等.风干扰下的四旋翼无人机ADRC控制律设计[J].测控技术,2016,35(9):47-51.

[6] 王欢.小型四旋翼无人直升机姿态控制技术研究[D].兰州:兰州交通大学, 2015.

[7] 吴瀚文.四旋翼飞行器抗风控制研究[D].哈尔滨:哈尔滨工业大学,2016.

[8] 肖业伦,金长江.大气扰动中的飞行原理[M].北京:国防工业出版社,1993.

[9] 李战东.垂直轴风力发电机气动性能研究[D].哈尔滨:哈尔滨工业大学,2012.

[10] KRISHNAMURTHY P,KHORRAMI F.A control design for Quad Rotor UAVs with input unmodeled dynamics[J].IFAC-PapersOnLine,2015,48(11):227-232.

[11] 边潇俊,林达,谢玉姣.基于滑膜控制和SAFNN的鲁棒混沌同步[J].四川理工学院学报:自然科学版,2015,28(5):44-50.

[12] 陈增辉.基于反步法的四旋翼飞行器控制方法研究[D].天津:天津工业大学,2016.

[13] 段国强,张岳军,李衍杰,等.四旋翼无人直升机控制算法仿真比较研究[J].计算机仿真,2014,31(4):78-82.

[14] 田聪玲.基于反步法的四旋翼飞行器非线性控制[D].哈尔滨:哈尔滨工业大学,2014.

[15] 刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2015.

[16] 高为炳.变结构控制的理论及设计方法[M].北京:科学出版社,1996.

Design of BSSA Controller for Unmanned Aerial Vehicle Disturbing to Wind Shear

XUJianxun

(School of Automation & Information Engineering, Sichuan University of Science & Engineering, Zigong 643000, China)

In order to overcome the problem that the four-rotor unmanned helicopter is unstable due to wind shear disturbance during flight, a backstepping sliding mode adaptive controller is designed. Firstly, the kinetic model of the UAV in the wind shear is established, and then the backstepping control and the sliding mode control method are combined to deduce and design the backstepping sliding mode adaptive controller. Finally, the simulation experiment is carried out in Simulink. The experimental results show that the backstepping sliding mode adaptive control (BSSA) and the backstepping adaptive controller (BSA) can further mitigate the effects of wind shear on UAVs, with stronger robustness.

wind shear; unmanned aerial vehicle; backstepping adaptive control; sliding mode control

1673-1549(2017)06-0047-07

10.11863/j.suse.2017.06.09

2017-09-18

徐建勋(1992-),男,湖北咸宁人,硕士生,主要从事智能控制与专家系统方面的研究,(E-mail)1322477784@qq.com

V249.1

A