关于高中物理解题方法的认识及应用探索

李梓萌

(湖南师范大学附属中学 410006)

关于高中物理解题方法的认识及应用探索

李梓萌

(湖南师范大学附属中学 410006)

高中阶段物理是培养学生理性思维与动手实践能力的一门重要学科，而习题的求解则也是学生必须要掌握的重要学习内容.文章主要以此为前提，重点对物理解题方法进行了分析，对于提升我们的物理学习水平具有重要意义.

高中；物理；解题方法；应用

物理学科本身体现了一定的逻辑性，当我们对其进行学习时，必须要运用正确的解题方法，才能达到事半功倍的效果.

一、微元法

所谓微元法，是数学与物理解题中十分常用的方法之一，这种解题方法在思维上主要呈现了从部分到整体的特点，使用一些十分常见的物理定律与规律，解决繁琐的物理过程，进而使问题简单化.微元法的运用，能够让学生在处理物理习题时，注重问题的微元部分，进而实现解决整体问题的目的.

图1

例1 如图1所示，小红身高为h，在灯下按照速度v进行水平直线行走.设置灯距地面的高是H，那么以此求人影顶端C为匀速直线运动.

解析在对这一题进行求解时，不能使用速度分解的方式进行求解，而是需要运用微元法.

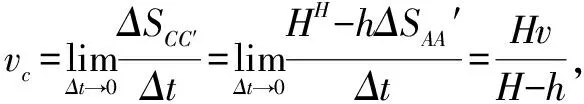
二、整体法

整体法这种解题思维较为特殊，与普通受力分析相区分，在解题中运用整体法，并不能够详细的对各个力的作用进行分析，而是在相关条件的基础上，将一些联系较为密切的物体作为一个整体，从而分析这个整体的受力情况.以此便能够将物体之间存在的繁琐的受力情况进行简单化，降低问题难度.

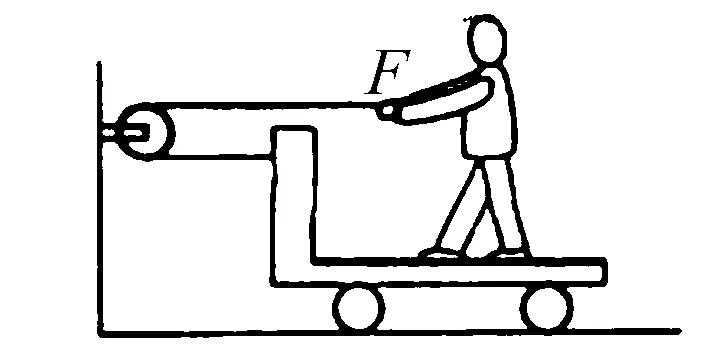
图2

例2 如图2所示，人与车的质量分别是m、M，人使用水平力F对绳子进行拉抻，两端绳子处于水平方向，若不计滑轮质量与摩擦力，且人与车始终处于相对静止的状态，水平地面光滑，那么计算车的加速度.

解析求解车的加速度，需要事先隔离车，进而完成求解.其实人与车始终处于相对静止的状态，也就是人与车加速度的相同，基于此，可以将人与车视为一个整体，针对这一整体使用牛顿第二定律便可完成求解.

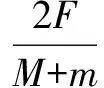
三、图像法

我们在学习物理知识时，了解图像和题干之间的关系非常必要，这主要是因为图像可以准确的反映出物理问题与要求，并且将物理问题简单化.

图3

例3 桌子上分别有一杯水和一杯酒精，其质量和初始温度相等，运用两个一致的加热器，对酒精和水分别进行加热(热量损失忽略不计)，图3是加热时温度受时间变化影响的图像.如此求a、b两种液体分别是什么?

解析因为这两种液体的加热时间和吸收热量相同，通过对图像的分析可以了解到，a、b两种液体初始温度是一致的，然而在加热相同的时间后，a液体温度要高于b液体，所以a液体温度变化也要超过b液体，这时便可以采用公式Q吸=cm△T计算得出a、b两种液体的比热容，即b液体的比热容要大于a液体，因此a液体为酒精，b液体为水.

四、对称法

高中阶段的物理习题中，难免有一些难度较大的习题，这时便可以使用对称法进行求解.对物理习题进行求解时，对称法本身是一种非常规的解题方式，然而却可以降低习题难度，提升我们解题的准确性.

如果使用传统的解题法，主要是运用力矩原理，然而力矩原理对于我们而言比较繁琐，使用时也比较容易出错.所以，实际求解物理习题时，针对这一类习题便可以运用对称法，既降低了题目的难度，将其更加直观、直接体现在我们面前，同时也可以全面提升解题效率.

综上所述，高中物理知识本身体现了一定的难度，我们平时在求解物理习题时，如果缺少有效的解题方法，便无法深入理解习题，通过微元法、整体法、图像法、对称法四种解题方法的运用，能够降低习题难度，并且全面提升我们的物理学习水平.

[1]许玉燕. 力学中“板块模型”的归类[J]. 数理化学习(高中版),2016,(08):44-45.

[2]卢跃祥. 浅议类平抛运动的基本应对策略[J]. 数理化学习(高中版),2016,(01):46.

[3]许冬保. 探究物理课程中微积分思想方法的隐性渗透与显化教学[J]. 课程教学研究,2015(01):70-73.

G632

A

1008-0333(2017)33-0045-02

2017-07-01

李梓萌(2000.1-)，男，湖南岳阳人，在读学生.

闫久毅]