粘弹性材料与钢的碰撞力学模型分析*
张 日,何禹忠,王修勇
(湖南科技大学 土木工程学院,湘潭 411201)
粘弹性材料与钢的碰撞力学模型分析*
张 日,何禹忠,王修勇
(湖南科技大学 土木工程学院,湘潭 411201)
近期碰撞调谐质量阻尼器(pounding tuned mass damper,简称PTMD)已经被提出来参与结构的振动控制.因为PTMD的碰撞过程主要由粘弹性材料与钢发生碰撞,所以其碰撞的力学模型是研究PTMD的关键因素.文章通过研究现有的粘弹性碰撞力模型,提出了一种不同的非线性碰撞力模型来模拟粘弹性材料与钢之间的碰撞力.同时通过碰撞实验得到重要系数并用粒子群算法对模型各项参数进行拟合.结果表明,该模型比现有的粘弹性碰撞力模型具有更好的性能.
碰撞调谐质量阻尼器;粘弹性材料;碰撞力学模型;粒子群智能算法
0 引言
当调谐到主结构的固有振动频率时,TMD能实现最有效地减振.然而,传统TMD的能量耗散能力非常有限,而且使TMD最优振动频率调谐为主结构的自振频率,这样才能达到较好的减振效果.而碰撞TMD是在传统的TMD基础上的改进,如图1、图2的模型所示.碰撞TMD是在TMD的两侧安装挡板限制TMD的行程,当结构受到振动时,m1与m2之间发生相对运动,在挡板和质量块间安装了一层粘弹性材料,当相对运动的行程大于挡板所限制的间隙时即发生碰撞,利用惯性力、碰撞力进行结构减振.碰撞TMD的设计思路是在质量块加上限位装置来限制其位移,使其能在遇到大幅振动时通过碰撞来达到更加显著的减振效果.确定了碰撞TMD的模型之后,接下来需要研究碰撞力模型.
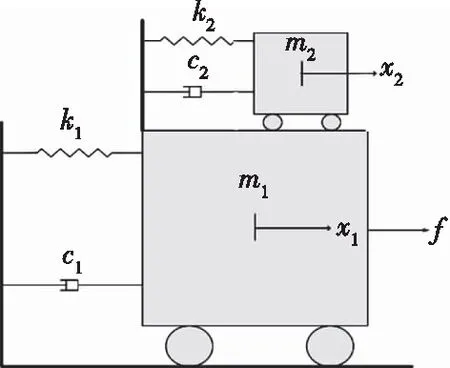
图1 TMD的模型示意图
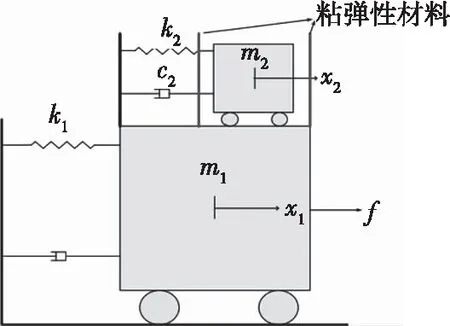
图2 碰撞TMD的模型示意图
1 碰撞模型的经典理论
1.1 古典碰撞模型
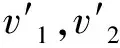
(1)
(2)
e为碰撞时的回弹系数,表达式如下:
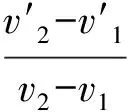
(3)
当e=1时,则表示该碰撞为完全弹性碰撞;当e=0时,表示该碰撞为完全塑性碰撞.经过试验知道e的取值与碰撞对象的材料与形状都有关系.所以这样使得该方法局限性较大.对于两碰撞结构采用多自由度进行模拟或者有多个物体相碰撞时,该方法都不适用.

1.2 线弹性模型
线弹性模型是一种最简单的弹性力分析模型,表示力随位移呈现线性变化,力与相对位移成线性关系.弹性力的表达式如下:
F=kδ(t)
(4)
式中,k为碰撞弹簧刚度,δ(t)为两碰撞物体在碰撞时发生的相对侵入位移,这个模型忽略接触中的能量损失,所以并不符合实际碰撞情况.
1.3 非线性粘弹性模型
改进的线性粘弹性模型十分简单且易于数值模拟.然而在碰撞开始时δ=0,由于压痕为0和非0的相对速度可能出现突然上升的碰撞力.为了克服这个缺点,Jankowski[1]提出非线性的粘弹性模型:
(5)
Jankowski[2]还修正了碰撞阻尼系数,他计算的阻尼系数表达式如下:
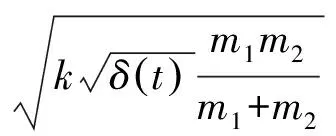
(6)
其中阻尼常数ξ为:

(7)
由于模型的分段表示,该模型下的碰撞力与位移的曲线在碰撞压缩阶段和恢复阶段之间不是光滑连续变化的.
1.4 Hunt-Crossley模型
由于碰撞问题的高度非线性,因此,非线性系数变成一个变量而不是固定的值,这种更为灵活的力学模型,称为Hunt-Crossley模型.这个模型里能量损失与当时的相对速度与缩进位移有关.Hunt-Crossley模型的一般形式为:
(8)
当非线性系数n=3/2时,Lankarani[3]and Ye[4]分别提出了如何求解ζ.如式(9)和(10)
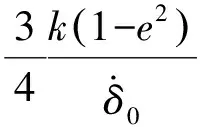
(9)
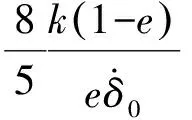
(10)
1.5 考虑表面残余形变提出的新碰撞模型
基于Lankarani和 Nikravesh[5]提出的碰撞模型在这个过程中的能量损耗完全取决于塑性变形和弹性力的存在.这个碰撞力模型还是存在一些问题,首先接近过程中只存在弹性力是不合理的.此外对于那些碰撞发生在相对速度较低的时候,塑性变形可能发生在表面.
(11)
结合以上优点与缺点,本文提出了一个既能全面考虑各个阶段的弹性与塑性力情况,也能模拟的更加准确的碰撞力学模型:
(12)
1.6 推导提出的新模型的ζ
根据经典的动能和动量守恒定理,在碰撞中损失的能量ΔE可以用恢复系数e和碰撞相对初始速度表示
(13)
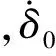
ΔE=ΔE1+ΔE2
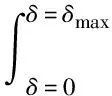
(14)
处理上式ΔE1可得:
(15)
为了解决ΔE1在此单自由度系统中,其刚度为非线性,运动方程为[6]:
(16)
(17)
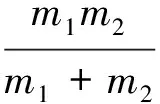
(18)
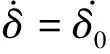
(19)
(20)
由碰撞力引起的能量损失ΔE1为
(21)
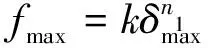
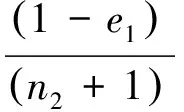
(22)
联立能量方程可以得到ζ的关系:
(23)
在该模型中,碰撞刚度k将通过模拟碰撞实验中观察到的最大碰撞力确定.残余表面形变率e1和恢复系数e可以通过碰撞试验得到.残余形变δe和碰撞阻尼ζ可以通过式(12)和(23)得到.在这个公式中应注意残余表面形变的能量损失不会超过整个碰撞过程中的能量损失.这个限制也就是:
ΔE≥ΔE2
(24)
通过式(14)可知
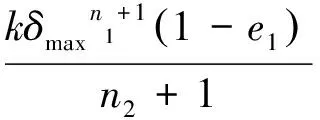
(25)
当特殊情况ΔE=ΔE2时会有在接近阶段时材料无阻尼情况,所以在接近阶段结束恢复期开始的阶段,应该有势能与动能相等的关系.
(26)
再联立式(25)和式(26)求出e与各项参数之间的关系
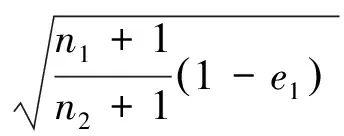
(27)
由式(27)可以看出最大的恢复系数必须满足这么一个关系
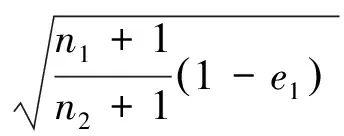
(28)
2 碰撞实验设计
由图3 可知碰撞实验模拟的是一个单摆情况下的碰撞情况,由位移计和传感器记录下数据.如图4可知粘弹性材料选取的是very high bonds简称VHB胶带,与球形钢构件的碰撞.
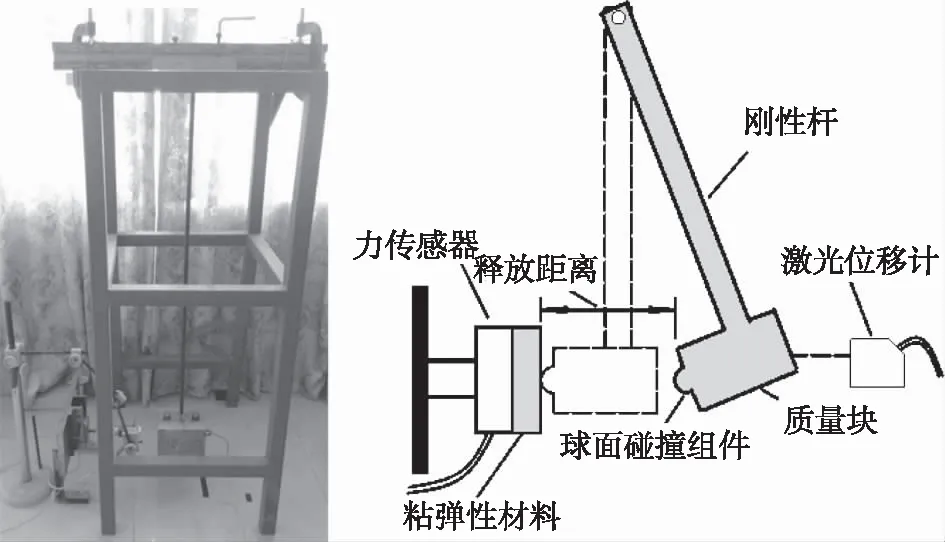
图3 碰撞模型整体设计图

图4 碰撞构件和VHB胶带
在本实验中,即使在不同的接近速度,如表1所示恢复系数保持在一个相对稳定的e从0.432到0.467变化.因此,采用平均值0.448作为钢与粘弹性材料碰撞的恢复系数e.如表2所示剩余表面变形率e1也相对比较稳定从0.766到0.792变化,这里我们也取其平均值0.780.
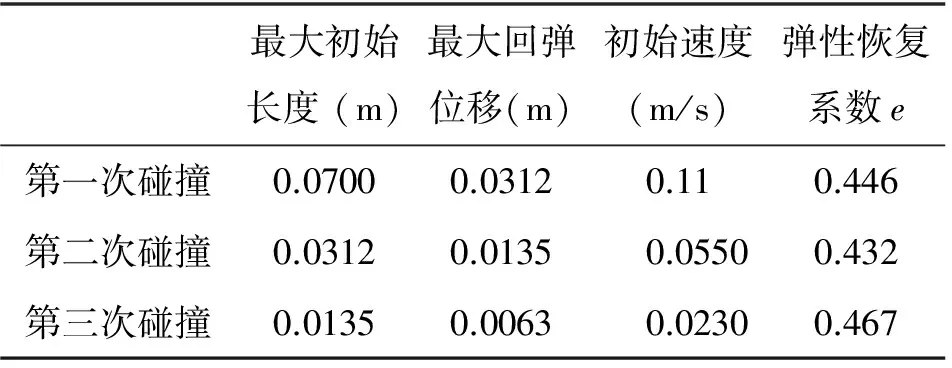
表1 不同碰撞速度下的弹性恢复系数
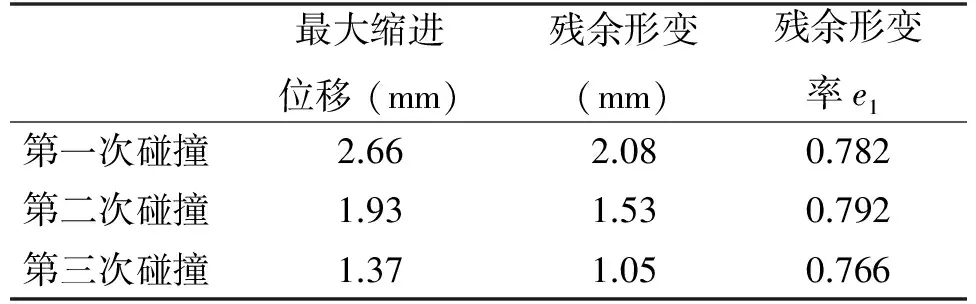
表2 不同碰撞速度下的残余形变率e1
由试验已知弹性恢复系数和残余形变率e=0.448,e1=0.780,利用新提出的模型来模拟该试验的第一次碰撞的碰撞力.
3 碰撞力非线性模型的粒子群算法
为了进一步解决该力学模型的关键参数,选择采用智能粒子群算法来完成参数辨识.粒子群算法[7],是一种基于迭代的优化算法.它最先是从随机的几个初始解出发,通过适应度关系来评估所获的逐个局部解的品质,不断更新迭代而寻找到新的目标.这种算法速度快、原理简单、且适用范围广,在实现情况复杂的参数寻忧问题中有着显著的优越性.

表3 粒子群算法优化的最佳参数
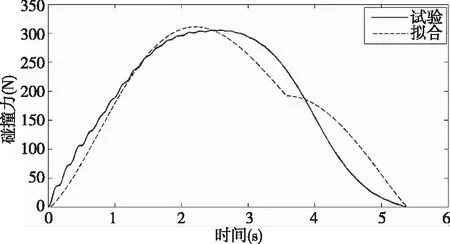
图5 智能算法粒子群拟合的碰撞力与时间

图6 智能算法粒子群拟合的位移与碰撞力
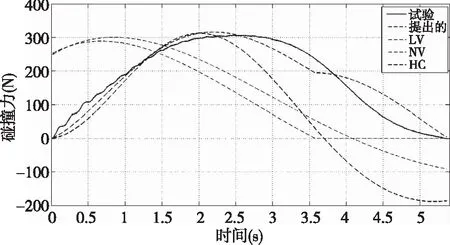
图7 VHB胶带试验与各个模型的比较

碰撞力模型碰撞刚度k碰撞阻尼ζ线性(LV)19881N/m0.2476非线性(NV)1953N/m1.50.8350Hunt⁃Crossley(HC)218932N/m1.53.9429×106新提出的197262N/m1.172.9717×105
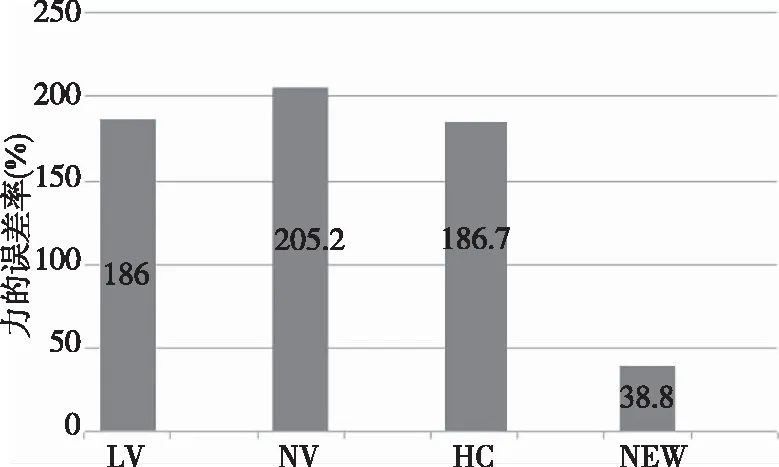
图8 碰撞力模型力的误差率比较
由图7 可知不同的碰撞力模型对实际情况的模拟.表4表示的不同力学模型求出的各项参数,由图8可知由力的均方差求出的误差率仅为38.8%,所以粒子群算法所得结果与其他现有力学模型相比更为准确,误差更小.
4 总结
本文考虑弹性后效的问题,从而提出新的力学模型,基于能量守恒以及智能控制算法拟合出在特定粘弹性材料中的各个参数,通过试验进一步证明了能够更加准确描述出力的图形.说明这个新模型对今后碰撞过程的研究以及碰撞TMD的设计有重要的研究意义.
[1] Jankowski R, Wilde K, Fujino Y. Pounding of Superstructure Segments in Isolated Elevated Bridge During Earthquakes[J]. Earthquake Engineering & Structural Dynamics, 1998, 27(5): 487-502.
[2] Jankowski R. Analytical Expression Between the Impact Damping Ratio and the Coefficient of Restitution in the Non-linear Viscoelastic Model of Structural Pounding[J]. Earthquake Engineering & Structural Dynamics, 2006, 35(4): 517-524.
[3] Lankarani H M, Nikravesh P E. A Contact Force Model with Hysteresis Damping for Impact Analysis of Multibody Systems[J]. Journal of Mechanical Design, 1990, 112(3): 369-376.
[4] Ye K, Li L, Zhu H. A Note on the Hertz Contact Model with Nonlinear Damping for Pounding Simulation[J]. Earthquake Engineering & Structural Dynamics, 2009, 38(9): 1135-1142.
[5] Lankarani H M, Nikravesh P E. Continuous Contact Force Models for Impact Analysis in Multibody Systems[J]. Nonlinear Dynamics, 1994, 5(2): 193-207.
[6] Khatiwada S, Chouw N, Butterworth J W. A Generic Structural Pounding Model Using Numerically Exact Displacement Proportional Damping[J]. Engineering Structures, 2014(62): 33-41.
[7] J. Kennedy, R. Eberhart. Particle Swarm Optimization[C].IEEE International Conference on Neural Networks, 1995. Proceedings. 1995(4):1942-1948.
AnalysisofImpactMechanicsModelBetweenViscoelasticMaterialandSteel
ZHANG Ri,HE Yu-zhong,WANG Xiu-yong
(School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411100, China)
Recently, the pounding tuned mass damper has been proposed to participate in the vibration control for structure. Because the collision process of PTMD is mainly caused by the pounding between viscoelastic material and steel, the mechanical model is the key factor to study the PTMD. The article proposes a new nonlinear impact force model to simulate the collision force between the viscoelastic material and steel by researching on the existing viscoelastic impact force model. At the same time, the impact experiments obtain important coefficient and particle swarm algorithm is used to fit the model parameters. The results show that the performance of the new model is better than the existing model.
pounding tuned mass damper; collision mechanics model; viscoelastic materials; particle swarm optimization
2017-05-18
张 日(1990-),男,硕士研究生,研究方向:结构振动控制.
王修勇(1962-),男,博士,教授,研究方向:结构振动控制.
TB324
A
1671-119X(2017)04-0081-05

