藏在简单错误中的“高级思维”

【摘要】做错题是学生在数学学习中普遍存在的现象，其价值值得教师关注和思考。教师可通过关注简单思维的“角落”，走到一般思维的“背面”，发现常态思维的“变式”，巧妙利用数学学习中的简单错误培养学生的“高级思维”。

【关键词】简单错误；“高级思维”；关注角落；走到背面；发现变式

【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009（2017）81-0029-03

【作者簡介】刘丽娜，江苏省常熟市实验小学（江苏常熟，215500）教师，一级教师。

黑格尔说：“错误本身是达到真理的一个必然的环节。”数学学习也是如此。看似简单的一个个错误，若能穿珠成串，让每一个错误都闪耀它的光芒，折射它的价值，那么错误将不再是糟粕，而是能让学生开出高级思维花朵的沃土。

一、关注简单思维的“角落”

即使再优秀的数学家也会犯错，错误并不可怕，只要能定点错误方位，深入分析，实现有效的自我反省，在被忽视的角落里挖掘亮点，就能使数学思维得到完善性的提升。

（一）肯定建构的视角，注入数形的力量

建构主义学习观强调给学习者整体性的任务，将学习者带入一个较为完整的问题情境之中，使他们搭建自己的思维体系，在学习过程中掌握相关的方法和知识。例如苏教版四下的一道习题：一本故事书共340页，丁丁看了4天后，剩下的比已经看的少100页，丁丁平均每天看多少页？

学生解题的本意不错，有理有据，步步为营，却不知误把100页当作剩下的页码，从而一步步出错，徒劳无功。若能将此类问题，在搭框、造架、填充后注入“数形结合”的思想——借助线段图，那本题的难点“求出已看的页数”也就能成功突破了。

学习并非个体获得越来越多的外部信息，而是学到越来越多有关认识事物的结构，不断搭建新的认知图式。解题时学生已有初步的建构视角，教师只需在此基础上引入图形解题法，学生的思维便能得到进一步延展。

（二）抚摸感性的触角，添加理性的因子

感性思维往往先入为主，有时能触发意想不到的灵感，美妙无穷。数学思维需要感性的猜想，同时，也与左脑的分析、逻辑、判断思维以及顺序的、线性的加工、处理信息的方式密不可分。例如苏教版四下的一道习题：

下面哪个算式与99×a+99结果相等？

A.99×（a+1）

B.99×a+1

C.a×（99+1）

有字母a又有特殊数99，学生往往会凭主观意愿让99+1凑成整百，认为这样就可以进行简便计算了，但对于这道题，这些学生的感性思维并不正确，此题必须按照“乘法分配律”来进行化简，不可感情用事。

思考若能分层，以线性模式割裂，一段一段地加以比对，也许有助于减少这种感性错误，促进理性的因子自然融入，相得益彰。

（三）寻找独特的转角，成就别样的精彩

普遍性思维固然容易理解，但独特性思维更能焕发光彩。我们欣赏常态性解题的缜密清晰，更期待个性化解题的多元奇特。例如苏教版六上的一道习题：

一般学生都会先求剩下的分率，再求总个数，最后求已经生产的个数。思路清楚明了，易于解答。但笔者的学生小准有不同的见解：先求剩下的份数，再求已经生产的是剩下的几分之几，最后求已经生产的个数。

独特的转角，确实有别样的风景：让学生再来仔细看看解题步骤，小准同学恍然大悟，原来第二步应求每一份是多少个玩具。这样的一次错误经历，让学生明白了独特转角固然好，要成就别样精彩还需严密细致的思路。

二、走到一般思维的“背面”

学生的数学思维总是带有一些惯性与倾向性，喜顺不喜逆，乐简畏惧繁，观静不思动，这样的导向性习惯，会让他们的思维深受桎梏，抑制其创新性思维的培养。思维的发展不仅是让原有的一般思维发挥所长，更是让独特与创新性思维得到开拓与生长。

（一）辩证思维：顺逆兼顾，最佳相遇

数学是蕴含着辩证性质的，在数学的多种对立环节中总存在着对立统一的关系，顺逆思维便是如此。如何在顺向思维、逆向思维中寻找最佳的相遇点？可行的思路是分析条件整合以后与结论的差异有多少，设法逐步消除这些差异。例如苏教版四下的一道习题：

师傅和徒弟加工同一种机器零件，8小时内，师傅加工了15盒，徒弟加工了9盒。徒弟共比师傅少加工48个。师傅和徒弟各加工多少个零件？

让学生分别说说数量关系式，就会发现学生的思维漏洞百出。教师可以引导学生思考：既可以从条件出发，又可以从问题反思。顺推：可求出徒弟比师傅少加工几盒、每盒多少个以及每小时少加工多少个；逆求：需知道师傅、徒弟各加工几盒以及每盒多少个。在顺逆推理中，便能知道这道题的关键点是“每盒多少个”。在有意义的求解过程中，必然会选择有用的条件而摈弃无用的条件（8小时内）。一般思维的唯一方向性得到巨大挑战，单向的思维习惯显然对解题无益，而双向的思维习惯可以更准、更佳、更快地打通思路。

（二）切换思维：繁简互逆，因地制宜

简单与繁复也是相对而言的，以简驭繁变换映射的思维方向显示了一种精确等价的便捷途径，但有些情形只能由简化繁，情况不同思路也就不同。例如苏教版五下的习题：

看似繁复，但必须繁复。繁简之间的不断变换，都应随机应变，不必过分追究繁简的形式，更应注重是否抓住了数学本质与相关联系，从而让思维的转换更具现实意义。

（三）动态思维：局部固定，模拟场景

动和静是事物状态的两个侧面，在数学教学中，动和静在同一个参照体系中既是相对的，又是可以相互转化的。例如苏教版四下的一道习题：

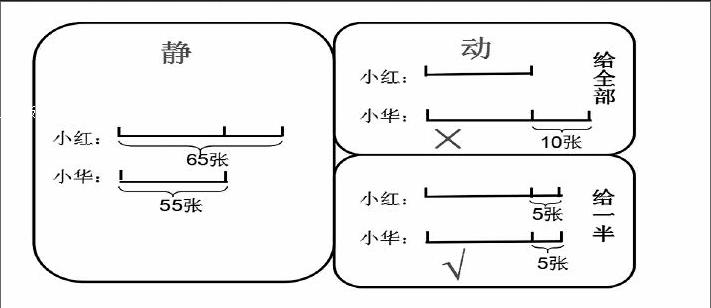
小红有65张邮票，小华有55张邮票。小红给小华（ ）张邮票后，两人的张数就一样多了。endprint

显然小华与小红相同部分的55张是局部固定的，而相差的10张就是该思考的部分。10张如何处理？化静为动，全给还是给一半？让画面动起来，在脑子里模拟两种场景，结论也就显而易见了。固定静态部分，活跃动态部分，脑海中丰富的画面感给解题带来了有效的支撑，提升了学生的解题能力，促进了其思维的质性飞跃。

三、发现常态思维的“变式”

语言在数学学习中扮演着重要的角色，学生正是借助镶嵌在数学中的语言游戏而获得数学知识，并且在师生对话、生生对话、自我对话中获取、修正、反省、重建数学语言体系。

（一）一词多义——巧读文本，从理到文

文本对话，即将即时性的讲话予以保留，使得数学内容以一种独白的形式展现出来。没有无缘无故的错，学生的错都是事出有因，错误的原因静静躺在笔尖，待有心人发现。例如苏教版四下的一道习题：

绕地球一周航海旅行，如果每天航行450千米，大约需要89天才能完成。绕地球一周大约要航行多少千米？

学生的解答：450×7=3150（千米）。何解？一场文字的沟通给了我们答案。学生看见“一周”便认为是一星期7天，7天和每天450千米，不是配套吗？而不知此“一周”与“一周”虽是同字，但绝非同义，查阅字典的功效在此处发挥得淋漓尽致。引导学生查字典发现：周：（1）圈子：地球绕太阳一～是一年。（2）星期：上～，下～。

回过头来，让学生自己与习题和错误对话，学生便能正确理解题意。题意的分析与解读，更能使学生的数学思维加深印记。

（二）一音多词——细磨要词，变窄为宽

心理活动是思维的产物，而口头对话则是思维的外显。口头对话是心理语言的一种输出，带有相互交流、纠正、深省的性质。例如苏教版四下的一道习题：

一列火车从甲地开往乙地，每小时行65千米，行了4小时后超过中点120千米，甲、乙两地相距多少千米？

这题的出错率非常高，出错症结大多没有注意关键词“中点”。在讲评题目时，教师请学生自己来解释“中点”“终点”的意思，学生举例“期中考试就是学期到一半时进行的考试”“期终考试是学期结束时的考试”。教师可以在学生充分理解了同音两词的意思后，进行对比题训练，变换关键条件，再让学生进行交流对话。

变换条件：A.行了4小时后超过中点120千米。B.行了4小时后超过终点120千米。

大多学生都有囫囵吞枣审题习惯，不会运用科学的带有理解性的读题方式解决问题。再次讨论后，学生的一些方法让人眼前一亮。圈画法：关键词句圈划；去杂法：多余条件划去；简图法：抽象条件画图；重读法：难懂条件讀两遍。

对话的生成，激活彼此的思维，将狭窄的就题论题思路变为宽阔的举一反三，给学生留下了深刻的记忆。可见，巧妙利用学生的错题也可激起千层浪，浪花朵朵绽开在学生常态思维的海面上，推陈出新，独特奇异。

错误就像水源，源源不断，清冽甘甜。教师应善用教学智慧，引导学生析错改错，逐步培养学生独特创新的批判性思维。于错误中沧海拾贝，品思维内光彩异常，甚是美好。笔者愿践行于教育前行之路上，涉足于心智蜕变之旅程，一路赏花观景，怡然自得……■

【参考文献】

[1]谢明初.数学教育中的建构主义[M].上海：华东师范大学出版社，2007.

[2]任樟辉.数学思维理论[M].南宁：广西教育出版社，2003.

[3]郑毓信.数学教育哲学的理论与实践[M].南宁：广西教育出版社，2008.

注：本文获2016年江苏省“教海探航”征文竞赛一等奖，有删改。endprint