KSS32-M型海洋重力仪动态性能分析
李秀敏, 付永涛, 周章国
KSS32-M型海洋重力仪动态性能分析
李秀敏1, 2, 付永涛1, 周章国1
(1. 中国科学院海洋地质与环境科学重点实验室, 中国科学院海洋研究所, 山东 青岛 266071; 2. 中国科学院大学, 北京 100049)
采用测网交点差、重复测线和与KSS31-M型海洋重力仪重合测线对比的方法, 利用近年来KSS32-M海洋重力仪的实测数据对KSS32-M海洋重力仪测量稳定性和数据可靠性进行分析。利用机动转向法验证重力仪阻尼延迟时间为70 s, 基于70 s阻尼延迟时间计算的重力测网的测量准确度为0.65 mGal, 与KSS31-M型海洋重力仪采集的重力剖面对比结果看, 重合测线相关性为高度相关, 4条重合测线网的交点差绝对值最大为1.66 mGal, 准确度为0.59 mGal, 均达到国家标准要求的近海重力测网交点差均方根小于2 mGal的技术指标。重复测线的幅值接近, 相位吻合, 匹配测点异常差的平均值小于0.9, 均方根均小于0.8, 相关性均在0.98以上。本研究表明KSS32-M型海洋重力仪动态测量性能稳定、测量数据可靠。
海洋重力测量; KSS32-M型海洋重力仪; 阻尼延迟时间; KSS31-M型海洋重力仪 ; 厄特渥斯
海洋重力测量是以海洋重力仪安装在船上, 在海面测量重力加速度的一种动态重力测量方法[1-3], 但是由于海上不可避免的海浪起伏, 航速与航向变化, 船内部的发动机等的机器震动, 海风、洋流等干扰因素使船体一直处于横摇、纵摇的运动状态, 要想获得高精度和高稳定性的重力测量数据依赖于工作性能稳定可靠、测量精度高的海洋重力测量设备的支持[4-6]。KSS32-M型海洋重力仪是德国Bodenseewerk公司在KSS31-M型海洋重力仪基础上升级研制的一种高性能海洋重力测量仪器[7], 而KSS31-M型海洋重力仪的测量性能已被广泛认可[8-12], 常作为其他重力仪测量性能分析的比较对象[13-15]。该型号海洋重力仪可以实时改正厄特渥斯效应的影响, 设计测量精度达到0.5 mGal, 具有低零点漂移和实时数据显示的特点, 并设计有直立弹簧避免交叉耦合效应的影响[16]。本文通过对KSS32-M型海洋重力仪的测网精度计算、重复测线的吻合程度对照以及与KSS31-M型海洋重力仪重合测线的对比, 分析其动态测量的性能。
1 阻尼延迟时间
实际作业中, KSS32-M重力仪某一时刻记录的数据并非此刻的重力读数, 而是延迟时间以前所在位置的读数, 即重力读数与GPS数据之间存在阻尼延迟时间[17]。重力数据在整理过程中需要作阻尼延迟时间校正, 阻尼延迟时间是影响重力测网准确度的重要因素, 重力仪生产厂方会提供阻尼延迟时间, 但是这个时间是否符合重力仪实际工作状态有待考证。付永涛等[10]提出可以利用船只机动转弯来观测KSS31-M海洋重力仪的阻尼延迟时间, 实际上就是利用重力观测值与厄特渥斯改正值之间对应的镜像关系来获取真实的阻尼延迟时间。
选择GSS32-M海洋重力仪2014年海试的测线段gb-2进行测线剖面分析, 在走航gb-2测线上, 有3次机动转向, 分别对应gb-2重力、航向和厄特渥斯剖面图(图1)中的A、B和C三点。在重力、航向和厄特渥斯剖面图(图1)上可以看到测量船沿275°方向航行至坐标轴时间14 504 s左右开始改变航向(A1点), 厄特渥斯变化响应时间(A2点)也是14 504 s, 重力在厄特渥斯的影响下发生明显的变化是在A3点, 对应时间是14 578 s。A3与A2的时间差为74 s, 重力发生突然变化的时刻与厄特渥斯响应时刻之间的时间差, 即为重力仪的阻尼延迟时间。利用这种方法对近3年来KSS32-M海洋重力仪在西太平洋地区采集的数据进行分析, 共寻找到38个机动转向点的重力延迟时间(如图2), 计算平均值为70.26 s。这个数值与宋文尧[18]利用重力仪倒台的方法得到的KSS30重力仪阻尼延迟时间70 s相吻合。

图1 测线gb-2的重力、航向和厄特渥斯剖面图
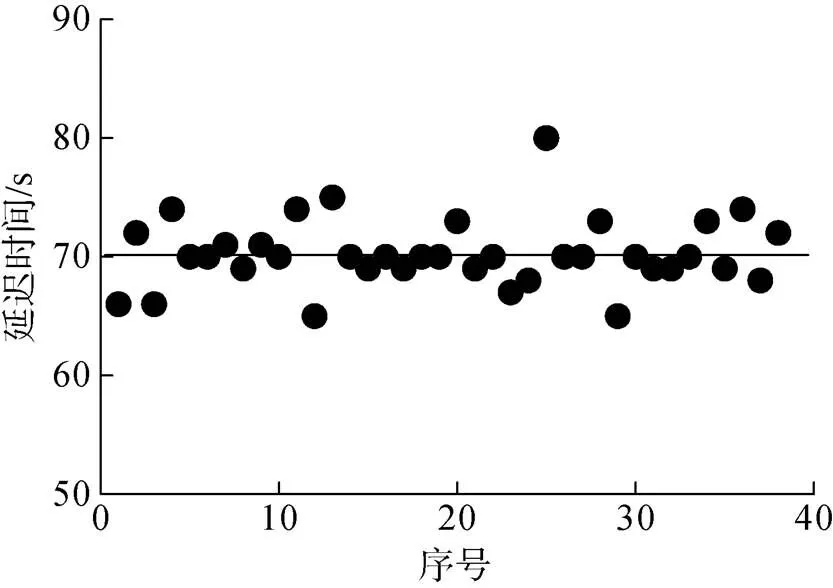
图2 重力数据延迟时间散点图
2 测线对比分析
2014年5月, 在青岛近海朝连岛海域布设测网对KSS32-M重力仪进行测试, 海况二级, 测网为东西向和南北向, 3条×3条, 每条测线长度25 km, 设计测线间距6 km (图3)。其中G1和G2测线是KSS31-M在2003年采集过数据的测线段, Z2测线与G2测线重合, L2测线与G1测线重合。
2.1 KSS32-M重力仪与KSS31-M重力仪重合测线
KSS31-M型重力仪测量精确度、可靠性和稳定性都很高, 已被业界认可, 在国内外海洋调查机构和研究所广泛使用, 所以采用KSS31-M重力仪实测数据与KSS32-M重力仪的数据进行比对, 以检验数据的可靠性。
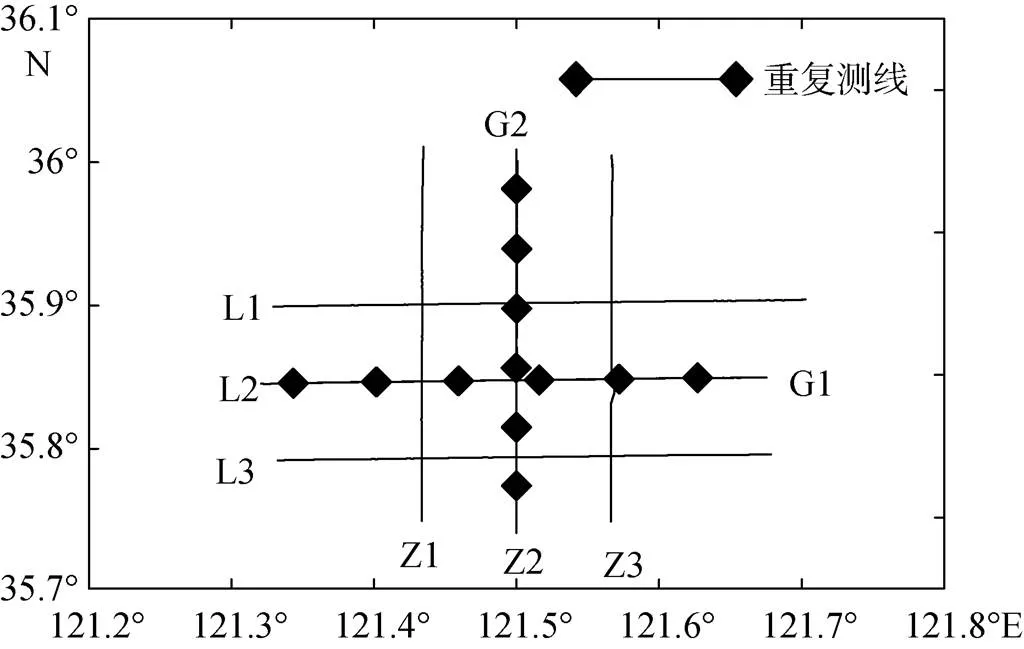
图3 KSS32-M重力仪的海试测网
Z2测线和L2测线在测试过程中受到的环境影响较小, 航迹与设定一致, 尤其是L2测线的航迹与G1的航迹基本重合, 其重力剖面与重合的G1测线重力剖面基本一致。两套重力仪所采集的数据的重合测线的幅值和相位均吻合, 这四条测线的交点差绝对值最大为1.66 mGal, 交点差均方根为0.59 mGal。
实际上, 由于Z2测线与G2测线的航迹有部分偏差, 因此其交点差也比较大(图4), 在航迹偏差大的区间, 重力的偏差也相对较大(图5), 最大为1.66 mGal。Z2测线与G2测线的相关系数为0.9975, 表明两条测线是高度正相关的。

图4 Z2和G2、L2和G1测线航迹图

图5 Z2和G2、L2和G1测线的重力剖面图
L2测线和G1测线的航迹基本吻合(图4), 其重力剖面也基本吻合(图5)。计算得到L2测线和G1测线的相关系数为0.9852, 表明两条测线的相关性为高度相关, 说明两套仪器在相同测点采集的数据基本相等, 体现了KSS32-M重力仪和KSS31-M重力仪之间的一致性。而KSS31-M海洋重力仪的准确度和可靠性已经被广泛证实, 因此可以佐证KSS32-M型海洋重力仪测量数据稳定可靠。
2.2 KSS32-M重力仪重复测线
对于海洋重力测量而言, 重复测量可以很好地反映测量设备的可靠性和稳定性, 在设计测试测网时, 测量船往返途中, 布设了两条重复测线gb-1和gb-2(图6)。但在测量船走航途中多次与渔船相遇, 并因避让渔船而转向, 导致这两条重力剖面匹配测点的均方根和平均值偏大, 两条测线匹配测点的平均值为2.82 mGal, 均方根为2.78 mGal。其自由空气异常如图6所示, 可以观察到两条测线的重力异常先增高, 经历一个较快速的下降然后又是一个波峰到波谷的过程。两条测线异常显示, 在躲避渔船转向的位置存在一定的幅值偏差, 在测线重合的位置所测得的重力异常在幅值和相位上是基本重合的, 总体来看两条测线的相位相同, 幅值偏差值接近。
从近年的测量数据中, 选取6段重复测线段进行定量分析KSS32-M型海洋重力仪的动态测量稳定性。重复测线段的空间重力异常如图7所示, 可见前后两次重复测量曲线拟合度非常高, 两条重复测线段的空间重力异常几乎重合, 相关系数都在0.996以上, 表明重合测线是高度相关的。将重复测线段测点数据按照距离最近的原则进行匹配后, 统计两条测线数据的离散程度, 计算差值的平均值和均方根, 结果如表1所示。从表中可知, 重复测线段的平均值最小仅为0.017 mGal, 最大的重复测线段为0.872 mGal,均方差的最小值仅为0.013 mGal, 最大值为0.793 mGal。在张向宇等[14]对GT-2M、KSS31-M和ZLS三种海洋重力仪的对比试验中, 对重复测线段所做的偏差统计平均值和均方根均介于0.2~0.8, 这里KSS32-M型海洋重力仪所采用的计算数据虽然与之不在同一工区, 但是偏差统计的结果具有一定的借鉴意义, 证明了该型号重力仪测量数据稳定、可靠。

图6 gb-1与gb-2重复测线的航迹与空间重力异常

图7 6段重复测线空间重力异常
表1 重复测线重力差值统计
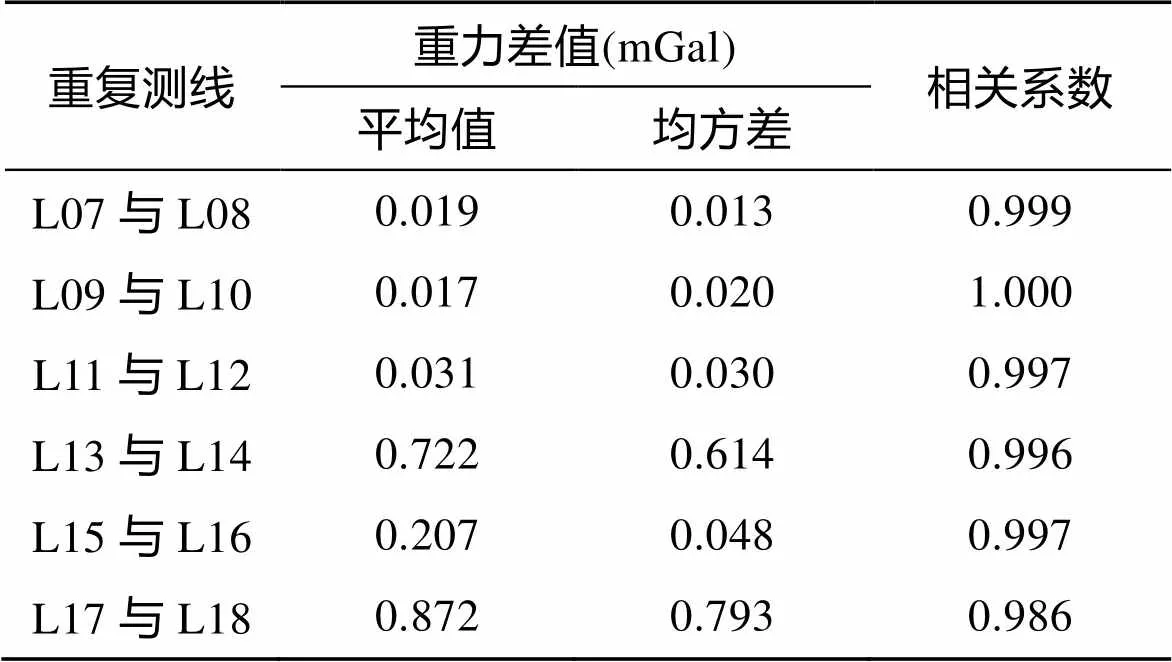
Tab.1 Deviation statistics for repeat survey lines
3 测网准确度
在重力测量工作中, 一般将测线布设为网状, 主副测线的交点处形成重复观测, 交点差是评价重力测量准确度的重要依据。布设的6条测线组成网格测网, 根据观测重力数据作出的空间重力异常剖面光滑无掉格毛刺等跳变。6条测线共有9个交点, 计算交点差的最大绝对值为1.05 mGal, 交点差均方根为0.65 mGal, 达到近海重力测网交点差均方根小于2 mGal的技术指标[19]。虽然测线交点差较少, 但仍可以作为KSS32-M型海洋重力仪测量稳定性和可靠性的一个参考。
4 结论
经过对KSS32-M型海洋重力仪阻尼延迟时间的计算, 采集的测网、重复测线以及与KSS31-M型海洋重力仪的重合测线的对比分析, 得出以下结论:
(1) 利用近年来实际测量资料, 统计38个机动转弯数据, 通过机动转向法计算验证KSS32-M型海洋重力仪的阻尼延迟时间为70 s。
(2) KSS32-M型海洋重力仪与KSS31-M型海洋重力仪采集的重力剖面对比结果表明, 重合测线高度相关, 4条测线的交点差绝对值最大为1.66 mGal, 交点差均方根为0.59 mGal, 均达到国家标准要求的近海重力测网交点差均方根小于2 mGal的技术指标。
(3) KSS32-M型海洋重力仪实测数据的重复测线方差均小于0.8, 平均值均小于0.9, 相关系数在0.98以上, 测试测网的准确度为0.65 mGal。
综上, KSS32-M型海洋重力仪相同测线段重复测量数据一致, 与KSS31-M重力仪重复测线段测量数据一致, 其测量数据可靠。
[1] 黄谟涛, 刘敏, 孙岚, 等. 海洋重力仪稳定性测试与零点漂移问题[J]. 海洋测绘, 2014, 34(6): 1-7. Huang Motao, Liu Min, Sun Lan, et al. Test and evaluation of the stability for marine gravimeter and its zero drift[J]. Hydrographic Surveying and Charting, 2014, 34(6): 1-7.
[2] 宁津生, 黄谟涛, 欧阳永忠, 等. 海空重力测量技术进展[J]. 海洋测绘, 2014, 34(3): 67-72, 76. Ning Jingsheng, Huang Motao, Ouyang Yongzhong, et al. Development of marine and airborne gravity measurement technologies[J]. Hydrographic Surveying and Charting , 2014, 34(3): 67-72, 76.
[3] 曾华霖. 重力场与重力勘探[M]. 北京: 地质出版社, 2005: 273. Zeng Hualin.Gravity Field and Gravity Exploration[M]. Beijing: Geological Publishing House, 2005: 273.
[4] 廖开训, 徐行. KSS31海洋重力仪的长期零点漂移特征[J]. 海洋测绘, 2015, 35(03): 32-35. Liao Kaixun, Xu Xing. Long tern zero drift characteristics of KSS31 marine gravimeter[J]. Hydrographic Surveying and Charting, 2015, 35(03): 32-35.
[5] 许时耕. GSS2型34号海洋重力仪13年零点漂移的分析[J]. 海洋技术, 1982, 1(4): 98-102. Xu Shigeng. Analysis of the zero drift of marine gravimeter model GSS-2 No.34 during its thirteen years of operation[J]. Journal of Ocean Technology, 1982, 1(4): 98-102.
[6] 张遴梁. 海洋重力仪的现状和发展[J]. 海洋科学, 2001, 25(9): 18-20.Zhang Linliang. Present state and development of marine gravimeters[J]. Marine Sciences, 2001, 25(9): 18-20.
[7] Bodensee Gravitymeter System. Instruction manual for marine gravity meter system KSS31M[R]. Germany: Bodenseewerk, 2004.
[8] 栾锡武. KSS31M型海洋重力仪在动、静态条件下观测到的读数变化及分析[J]. 地球物理学进展, 2004, 19(2): 442-448. Luan Xiwu.The fixed points gravity data measurment used by KSS31M and data analysis[J]. Progress in Geophysics, 2004, 19 (2): 442-448.
[9] 王秀东, 王真, 王先超, 等. KSS31M型海洋重力仪阻尼延迟时间修正后对重力测网精度的影响[J]. 海洋通报, 2010, 39(3): 320-323. Wang Xiudong, Wang Zhen, Wang Xianchao, et al. Effect of the corrected KSS31M marine gravity-meter's delay-time on the marine gravity measurement precision[J]. Marine Science Bulletin, 2010, 39(3): 320-323.
[10] 付永涛, 王先超, 谢天峰. KSS31 M型海洋重力仪动态性能的分析[J]. 海洋科学, 2007, 31(6): 29-33. Fu Yongtao, Wang Xianchao, Xie Tianfeng. Verfying the dynamic properties of KSS31M marine gravimeter by the observed gravity reading and GPS data[J]. Marine Sciences, 2007, 31(6): 29-33.
[11] 顾兆峰, 张志珣, 杨慧良, 等. KSS 31M海洋重力仪静态观测结果及分析[J]. 海洋测绘, 2005, 25(2): 66-68. Gu Zhaofeng, Zhang Zhixun, Yang Huiliang, et al.The static measurement result of KSS31M marine gravimeter and its analysis[J]. Hydrographic Surveying and Charting, 2005, 25(2): 66-68.
[12] 付永涛, 王先超, 谢天峰. KSS31 M型海洋重力仪在海边静态观测的结果——兼与栾锡武先生商榷[J]. 地球物理学进展, 2007, 22(1): 308-311. Fu Yongtao, Wang Xianchao, Xie Tianfeng. The static measurement of KSS31M marine gravity meter at coast[J]. Process in Geophysics, 2007, 22(1): 308-311.
[13] 张振波, 赵俊峰, 付永涛, 等. GT-1M海洋重力仪与KSS31M海洋重力仪的对比[J]. 海洋科学, 2015, 39(5): 85-91. Zhang Zhenbo, Zhao Junfeng, Fu Yongtao, et al. The comparison between GT-1M and KSS31M marine Gravitymeters[J]. Marine Sciences, 2015, 39 (5): 85-91.
[14] 张向宇, 徐行, 廖开训, 等. 多型号海洋重力仪的海上比测结果分析[J]. 海洋测绘, 2015, 35(5): 71-74, 78. Zhang Xiangyu, Xu Xing, Liao Kaixun, et al. Test analysis of difference coefficient calculations for surface ocean geostrophic currents[J]. Hydrographic Surveying and Charting, 2015, 35(5): 71-74, 78.
[15] 王功祥, 赵强, 廖开训. 浅谈当今海洋重磁调查设备的现状[J]. 南海地质研究, 2004, 17(1): 75-81. Wang Gongxiang, Zhao Qiang, Liao Kaixun. Simple discussion about the actuality of marine gravity and magnetism survey device[J]. Gresearch of Eological South China Sea, 2004, 17(1): 75-81.
[16] Bodensee Gravitymeter System. Marine gravity meter KSS32-M instruction manual[R]. Germany: Bodenseewerk, 2011.
[17] 陈邦彦, 梁广胜. 海洋重力测量和KSS31型重力仪[J].海洋地质, 1998, 35(3): 8-21. Chen Bangyan, Liang Guangsheng. Marine gravity measurement and KSS31-type gravimeter[J]. Marine Geology, 1998, 35(3): 8-21.
[18] 宋文尧. 海洋定位重力测量及其地质地球物理解释[M]. 北京: 科学出版社, 1993: 267. Song Wenyao. Ocean Orientation Gravimetric Survey and its Geophysical and Geophysical Interpretation[M]. Beijing: Science Press, 1993: 267.
[19] GB/T12763.8-2007. 海洋调查规范-第8部分: 海洋地质地球物理调查[S]. GB/T12763.8-2007. Marine survey specification - part 8: Marine geological and geophysical survey[S].
(本文编辑: 刘珊珊)
Dynamic performance testing of the KSS32-M marine gravimeter
LI Xiu-min1, 2, FU Yong-tao1, ZHOU Zhang-guo1
(1. Key Laboratory of Marine Geology and Environment, Institute of Oceanology, the Chinese Academy of Sciences, Qingdao 266071, China, 2. University of the Chinese Academy of Sciences, Beijing 100049, China)
Based on the data measured using the KSS32-M ocean gravimeter in recent years, the measurement stability and data reliability of this instrument are analyzed; moreover, the methods employed to measure the intersection point difference, repeating survey line, and coincidence line using the gravimeter are compared. The delay time of the gravimeter is 70 s, calculated using the maneuver steering method. Based on this calculation, the accuracy of gravimetric measurement is found to be 0.65 mGal. According to the gravity profile collected by the gravimeter, the correlations of the coincidence lines are highly correlated. The absolute value of the intersecting point difference of four coincident surveying lines is 1.66 mGal, and the precision is 0.59 mGal. All data meet the national standard of the intersection which the gravity measurement network of the national standard of the intersection point difference that less than 2 mGal. The average value of the anomalies of the matching points is less than 0.9, the variance is less than 0.8, and the correlation is higher than 0.98. In summary, this study shows that the data measured by the KSS32-M gravimeter are stable and reliable.
marine gravimetry; KSS32-M marine gravimeter; damping delay time; KSS31-M marine gravimeter; Oetworth
Strategic Priority Research Program of the Chinese Academy of Sciences, No.XDA1103010102]
Nov. 17, 2016
P738.2
A
1000-3096(2017)08-0064-06
10.11759/hykx20161117002
2016-11-17;
2017-01-15
中国科学院战略性先导科技专项海洋重磁场特征(XDA1103010102)
李秀敏(1991-), 男, 山东临沂人, 硕士研究生, 主要从事海洋重磁数据处理与解释研究, 电话: 13373882639, E-mail: 446729432@ qq.com; 付永涛,通信作者, 男, 副研究员, E-mail: ytfu@qdio.ac.cn

