改进灰色聚类法在洪水分级中的运用

张志燕

（山西省水利水电勘测设计研究院，山西 太原 030024）

改进灰色聚类法在洪水分级中的运用

张志燕

（山西省水利水电勘测设计研究院，山西 太原 030024）

对于判断灰类，以往白化权函数经常会发生隶属度重复的问题，用由传统白化权函数与中心点白化权函数组合而成的白化权函数，针对传统灰色聚类法使用阀值法计算指标权重存在的主观性强且权重会受指标分级跨度影响的问题，提出变异系数法计算指标权重，以改进灰色聚类法。选取能够反映洪水特性的4个指标，针对10场洪水的4个指标，使用变异系数法与改进的白化权函数分别计算指标权重、白化权函数值，确定每1个洪水等级，结合指标权重与相应的白化权函数值计算综合聚类系数，根据最大原则对洪水进行分级。

变异系数法；改进白化权函数；灰色聚类法；洪水分级

1 引言

在洪水分级的基础上，对洪水进行分级预测，能够提高预测精度，同时洪水分级还能为防洪调度决策、洪灾管理提供依据。传统灰色聚类法在确定指标权重时，存在各个指标分级跨度不同导致权重分配不合理[1]和主观性的缺点，提出使用变异系数法以代替传统灰色聚类法使用的阀值法来计算指标权重。与此同时，又结合传统、中心点白化权函数，引入闫滨等提出的一种改进白化权函数，以改进以往白化权函数判断灰类时，隶属度重叠的不足[2]。

以10场历史洪水为例，使用上述改进方法对其进行分级，以期能为洪水预测、防洪调度、洪水灾害管理提供依据。

2 变异系数法计算权重

变异系数法认为，当一个能够反映出对象间的差异越大，说明这个指标的区别度就越好，所以应该给这个指标赋予更大的权重，反之，如果每一个对象对同一个指标的指标值差别不大，则这个指标区分度就不大，所以应该赋予较小的权重。即根据“指标变异程度越大则给这个指标赋的权就越大”的原则进行赋权[3]。计算步骤如下：

设有n个分期对象，m个指标，则可以得到样本矩阵X：

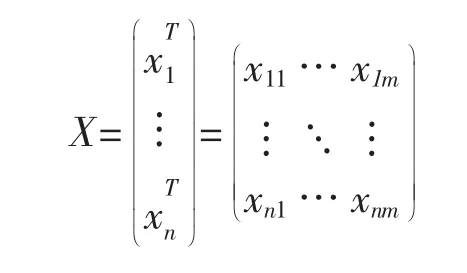
以上矩阵，对某一场洪水（序号为i）的第j项指标值为xij。

对于每一个指标，可以通过（1）式计算其变异系数：

其中Sj分别为对应指标的均值和标准差。

最后可以通过（2）式计算各个指标的权重。

3 改进灰色聚类法划分洪水等级

3.1 数据处理

对以样本阵X：

通过对样本阵X的规范化可以等到标准化阵Y：

其中变化的方法采用极差变换法，此法可使变换后的数据取值在0—1之间[4]。具体公式如下：

对于正向指标：

对于逆向指标：

3.2 制定分类标准

根据常识，对每一项指标，定义特大洪水、大洪水、中洪水、小洪水的分级区间为其中为标准化后，指标j的平均值。

3.3 构造白化权函数

采用改进的白化权函数，即上、下测度白化权函数采用传统的白化权函数，适中测度白化权函数采用基于中心点三角白化权函数，具体形式如下：

周启明有点紧张，钱海燕在旁边安慰他说：“不就是个结节嘛，没事的。”但医生建议他们最好马上去复查。钱海燕陪周启明去了宁波最大的医院。各项检查下来，医生皱着眉头说：“状况不太好，最好马上手术，很大概率是恶性的。”

其中λa、λa-1、λb、λb-1、λ1、λ2为中心点，这里取对应洪水区间的中点。

3.4 计算综合聚类系数

综合聚类系数由下式算得：

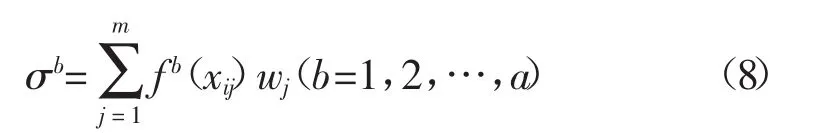
其中σb为综合聚类系数。

3.5 对洪水进行等级划分

任意一个对象b属于哪一个灰类通过下面方法判定，若：

则断定对象b属于灰类b*。

4 实例演算

据统计，浊漳河流域多年平均降水量为593 mm，流域内各站点实测最大降水量达1 503.6 mm（沁县南泉1976年），实测最小年降水量仅217.5 mm（武乡蟠龙1957年）。该流域雨量的73%来自汛期。

4.1 洪水等级划分前的准备

选取浊漳河流域内1963—2008年的10场洪水为研究对象，并选取能反映洪水特性的4个因子为影响因子，分别为：洪量、洪峰流量、洪水历时、径流深。这样便构建了一个有序样本X，样本容量为10，每个样本均为4维向量。具体数据见表1。

表1 洪水特征指标

4.2 权重的求取

在计算出各个指标的均值和标准差后，采用（1）～（2）式计算出洪量、洪峰流量、洪水历时、径流深四个指标的权重分别为：0.29、0.16、0.26、0.29。

4.3 数据处理

由于样本X指标单位不同，样本指标的特征值需要进行规范化，由于全部都是正向指标（值越大，洪水等级越高），所以使用（3）式对表1中的数据进行标准化，得到序样本Y，见表2。

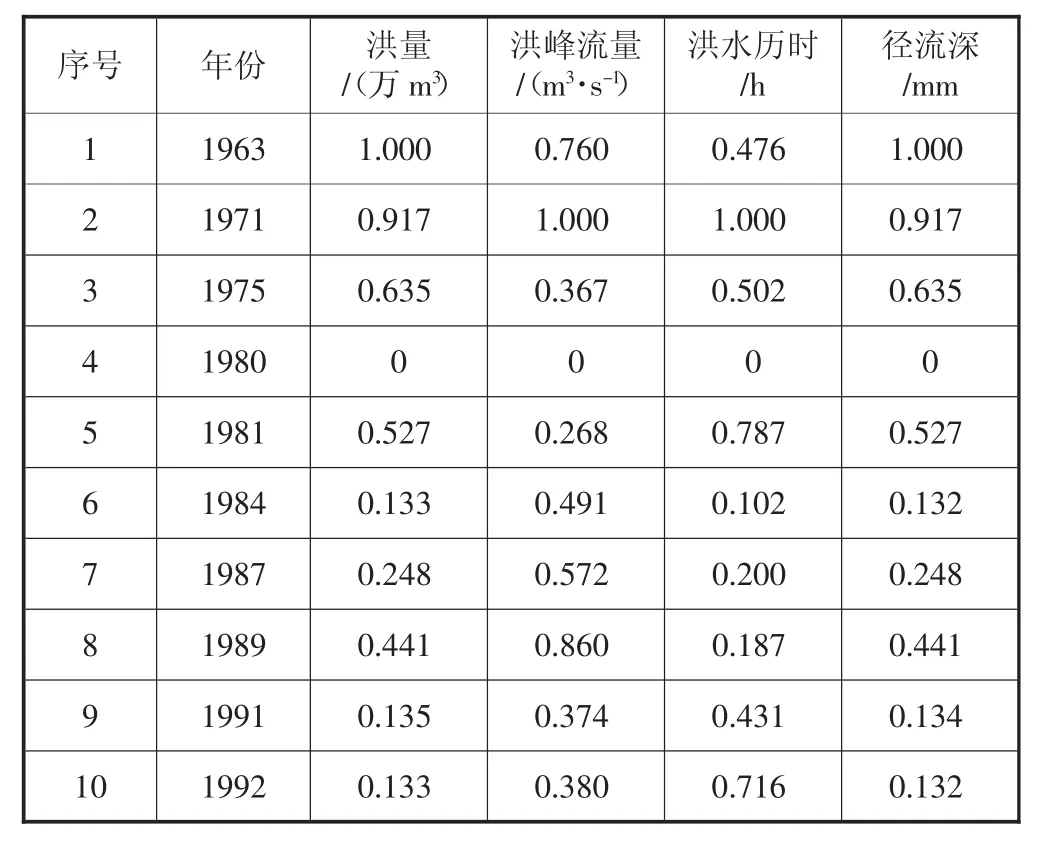
表2 指标标准化数值

4.4 分类标准的制定

根据洪水分类区间的中点可以制定出中心点见表3。

4.5 综合聚类系数的计算

对以每一个洪水等级，可以根据每一年各个指标所对应的中心点，选择合适的白化权函数，计算与这个洪水等级的隶属度，其中每一个等级所使用的白化权函数为：小洪水使用（7）式计算其白化权函数的值，中洪水与大洪水使用（6）式计算其白化权函数的值，特大洪水使用（5）式计算其白化权函数的值。最后通过（8）式计算各年份对以这个洪水等级的综合聚类系数。见表4。

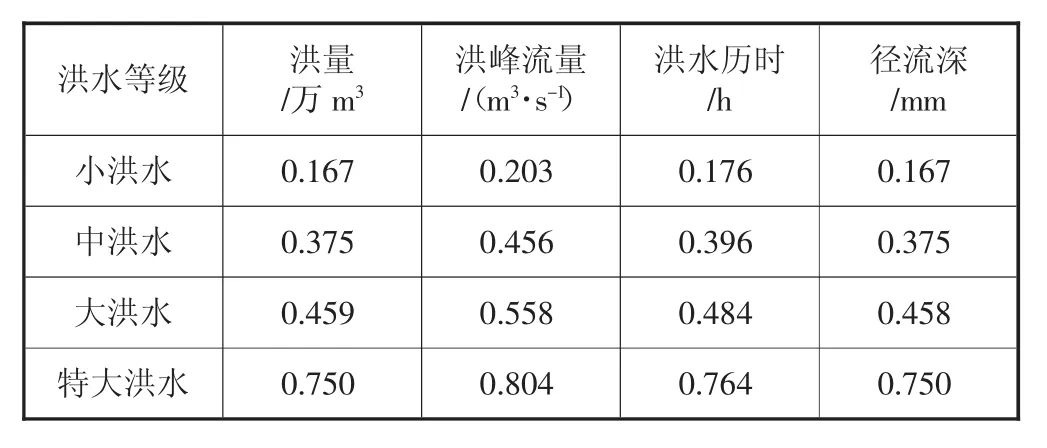
表3 中心点统计

表4 综合聚类系数统计

4.6 洪水的等级划分

根据本文3.5部分提出的原则，对洪水进行等级划分，划分结果见表4最右列所示。

4.7 比较分析

为了验证分类结果的合理性，本次选取传统灰色聚类法进行洪水等级划分，对两种方法进行比较分析。

4.7.1 灰色聚类法

传统的灰色聚类法计算指标权重所用的方法为阀值法[6]，计算结果见表5。

表5 指标权重

使用传统的白化权函数计算出白化权函数值，再使用（8）式计算出综合聚类系数，见表6。各个洪水的分级结果见表6最右列所示。

表6 传统灰色聚类综合聚类系数统计

4.7.2 两种方法对比

两种方法的分级结果见表7。

表7 两种方法结果对比

从表7中可以看出两个方法计算的结果大体一致，只有1981年洪水的等级划分得不一致。从表1可以看，1981年的洪水的洪峰流量、洪量、径流深比1971、1963的洪水（两个方法都把这两年的洪水都划分为特大洪水）的都小，甚至1981年的洪水的洪峰流量、洪量、径流深比1975年的洪水（两个方法都把这一年的洪水都划分为大洪水）的还小。而山西的洪水大多按照其洪峰、洪量作为主要指标进行防汛的，所以可以认为改进灰色聚类法把1981的洪水划分为大洪水是比较具有实际意义的，同时改进的灰色聚类法把1981年的洪水划分为大洪水，可以相应的降低防洪等级，对以防洪调度可以节约一定的防洪成本，同时减少水库防洪库容提高水库的兴利作用。

同时使用变异系数法计算指标权重能够克服传统阀值法计算指标权重存在主观性强，且权重会受指标分级跨度影响的不足；且改进的白化权函数可以克服传统白化权函数隶属度重叠的问题，所以本文提出的改进灰色聚类法对于洪水分级具有适用性。

5 结论

从洪水分级的数学本质为研究的点，使用改进的灰色聚类法对浊漳河流域的历史洪水进行分级，并与传统灰色聚类法的计算结果进行比较，经过分析发现，改进的灰色聚类法能够克服指标权重确定过程中的主观性和传统白化权函数隶属度重叠的不足，结果可信，适用于洪水分级。不足之处为其分类标准和分类数目都需要预先给定。

［1］蒋知栋，李晶，高杨，等.基于改进灰色聚类模型的矿区耕地损毁程度评价［J］.中国生态农业学报，2013，21（6）：765－771.

［2］闫滨，孙友良，于保慧.基于改进白化权函数灰色聚类法的水闸安全评价［J］.沈阳农业大学学报，2015，46（2）：245－249.

［3］周玲玲，王琳，刘伟峰，等.基于客观组合赋权法的即墨市水资源可持续利用评价［J］.水资源与水工程学报，2014，25（4）：50－55.

［4］李美娟，陈国宏，陈衍泰.综合评价中指标标准化方法研究［J］.中国管理科学，2004（12）：45－48.

［5］王文圣，李跃清，秦宁生.基于集对分析的洪水分类研究［J］.高原山地气象研究，2009，29（1）：51－54.

［6］胡丽慧，潘安，李铁松.灰色聚类法在升钟水库水体富营养化评价中的应用［J］.农业环境科学学报，2008（06）：2 407－2 412.

P338

C

1004-7042（2017）11-0034-04

张志燕（1978-），女，2005年毕业于太原理工大学土木工程专业，工程师。

2017-09-20；

2017-10-24