避开无穷 返璞归真（上）

文︳张景中 彭翕成

避开无穷 返璞归真（上）

文︳张景中 彭翕成

数学中的无穷，常用符号∞表示，来自于拉丁文的“infinitas”，取“没有边界”之义。

无穷内容之丰富，就像一个深不可测的海洋，其中不知蕴藏着多少秘密。古今中外关于无穷的著作浩如烟海。

对于无穷，数学家又爱又恨。面对无穷，常常能避则避，但避开无穷不是一件容易的事情。

1.《几何原本》中的无穷

欧几里得《几何原本》中第五公设就涉及无穷。叙述如下：

如图1，如果一条线段与两条直线相交，在某一侧的内角和小于两直角的和，那么这两条直线在不断延伸后，会在内角和小于两直角和的一侧相交。

图1

这里“不断延伸”的字句，已经涉及无穷。

“由圆外一点P向⊙O作切线”，现在常见的的作图法如图2，连接OP，作OP中点M，以M为圆心，MO为半径作圆，交⊙O于N，则PN即为所求作的切线。

而《几何原本》中的作图法如图3，连接OP，交⊙O于A，过A作OP的垂线，交以O为圆心，OP为半径的圆于点B，连接OB，交以O为圆心，OA为半径的圆于点C，则PC即为所求作的切线。

图2

图3

为什么《几何原本》中不采用图2的简单作法呢？因为圆的直径所对的圆周角为直角，是由三角形内角和等于180°推导得到的。使用图3的作法，就是希望避开平行公设，也就是避开无穷。

素数有无穷多个，在《几何原本》中的说法却是“质数比任意给定的一群质数还多”。注意这里避开了无穷。

2.从有限到无穷——三角形内角和定理的证

理解无穷，要从有穷开始。

研究表明：通过验证一个三角形的内角和为180°，就能断言所有三角形的内角和都为180°！

首先把几何问题代数化。如图4，建立平面直角坐标系，设△ABC的三个顶点坐标分别为A（0，0），B（1，0），C（u1，u2）。取 BC 的中点 M，延长AM至D，使得DM=AM，则∠DCB=∠CBA。取AC的中点N，延长BN至E，使得NE=NB，则∠ECA=∠CAB。于是要证明的命题转化为：∠ECA+∠ACB+∠DCB=180°，也就是 D，C，E 三点共线。

设 M（x1，x2），N（x3，x4），D（x5，x6），E（x7，x8），则命题的假设条件为 H：f1=2x1-（u1+1）=0，f2=2x2-u2=0，方程f1，f2表示M是BC的中点。

f3=2x3-u1=0，f4=2x4-u2=0，方程 f3，f4表示 N 是AC的中点。

f5=x5-2x1=0，f6=x6-2x2=0，方程 f5，f6表示 AM 延长1倍到D。

f7=x7-2x3+1=0，f8=x8-2x4=0，方程 f7，f8表示 BN延长1倍到E。

而要证明的结论是D，C，E三点共线，即C：g=（x5-u1）（x8-u2）-（x7-u1）（x6-u2）=0。

问题一共涉及10个变元。其中u1，u2可任意取值，叫做自由变元。一旦 u1，u2定了，x1～x8都可以由条件H定下来，所以x1～x8叫做约束变元。利用条件H接触x1～x8代入C，可得到关于u1，u2的多项式 G（u1，u2）。要证明条件H 之下有结论 C，也就是证明多项式G（u1，u2）恒等于0。容易推出G关于u1，u2的次数都不超过1，于是只要在u1，u2的一个2×2的格阵上检验G是否为0即可。这个格阵可取（0，0）、（0，1）、（1，0）、（1，1），立刻可以算出G在这几组数值下为0。事实上，对于（u1，u2）=（0，0）=（1，0）根本不用算，因为此时 A，B，C 三点共线，结论显然。而在（u1，u2）=（1，1）和（u1，u2）=（0，1）这两种情形下得到的△ABC是全等的。因而只要对（u1，u2）=（0，1）作检验即可。把 u1=0，u2=1代入 H，得 x8=1，x6=1，x7=-1，x5=1，代入 C 得 g=0，这就完成了命题的证明。（参阅《自然杂志》1991年第1期《举例子能证明几何定理吗》）

图4

这表明，只要检验4个三角形（实质上是一个），便足以证明三角形内角和定理！

3.“飞矢不动”中的无穷

古希腊著名哲学家芝诺曾经提出“飞矢不动”的怪论。他说箭在每一个时刻都有一个确定的位置，因而在每一个时刻都没有动。既然每个时刻都没有动，它怎么能够动呢？

为了驳倒这个怪论，就要说清楚什么叫动，什么叫没有动。

如果一个物体的位置在时刻u和后来的一个时刻v不同，我们就说它在时刻u和v之间动了。反过来，如果它在任意时刻t∈［u，v］都有相同的位置，就说它在u到v这段时间内没有动。

这样，动或不动都是涉及两个时刻的概念。芝诺所说“在每一个时刻都没有动”的论断是没有意义的！

芝诺论题的令人迷惑之处，在于运动物体好像要经过无穷多个时刻才能完成运动。而我们在理清动与不动的概念时，可以避开无穷，只在两个时刻考虑。

4.避开无穷的天才——阿基米德

古希腊的阿基米德是避开无穷的天才。他从抛物线弓形的内接三角形面积出发，成功地求出了抛物线弓形的面积。

如图5，设抛物线的方程为y=kx2（k＞0）。考虑区间［a-h，a+h］上的一段抛物线所构成的弓形。

图5

从抛物线弓形去掉这个三角形之后，剩两个小弓形。类似地作每个小弓形的内接三角形；重复操作，剩4个小弓形，如图6。作每个小弓形的内接三角形，其面积为k·）3。

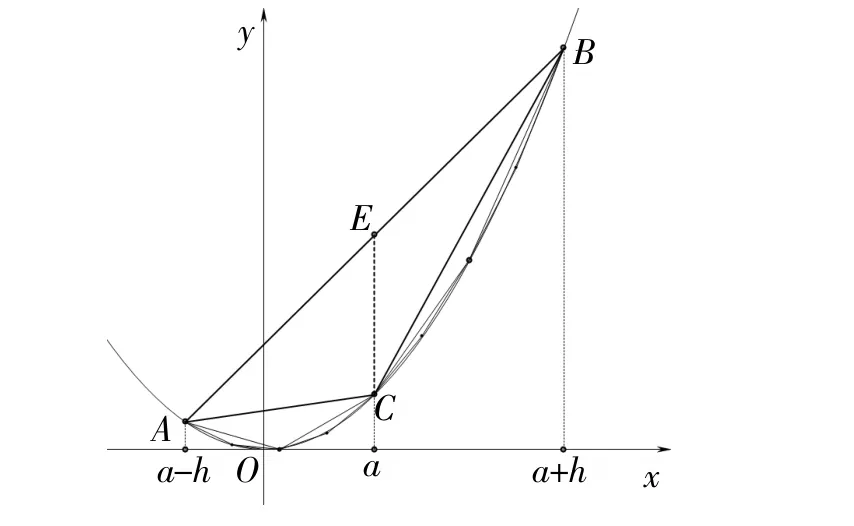
图6

不断做下去，得到无穷多的三角形，它们的面积之和是

在阿基米德时代，他必须避开无穷，说出一个令人信服的理由。

阿基米德计算到第n项就打住，得到等式

这个方法在数学史上以“穷竭法”著称。

（待续）