图形计算器的应用与思考

文︳周思宇 刘红卫

图形计算器的应用与思考

文︳周思宇 刘红卫

图形计算器是指可以绘制函数图像、解高次方程或多元方程组，以及能执行其他复杂操作的手持计算器，大多数图形计算器还能编写数学类程序。为了提升教学的信息化，使数学教学不抽象，很多中学以图形计算器为主体，相继建立了“e-数学实验室”，以此鼓励学生利用图形计算器等信息化手段对知识进行深入探索和挖掘。学生利用图形计算器可以将繁琐的数学运算变得简单，将抽象的数学概念变得直观，学生的思维过程可以逐步呈现。因此，教师在教学时利用图形计算器教学，助推学生思维的发展，将新课程推进到一个较高的水准。

一、图形计算器的应用

人教版（A）数学教材选修2-3中，在线性回归方程这一内容中，给出了对于一组具有线性相关的数据（x1,y1），（x2,y2），…，（xn，yn），其回归直线y=bx+a的斜率和截距可利用最小二乘法求解。但是用最小二乘法求回归直线计算量非常大，会使得学生产生疲倦的心理。如果在课堂上让学生利用图形计算器求回归直线，不仅可以提高学生的积极性，也有利于学生对知识的掌握。下面笔者选取一道与现实生活联系密切的题目进行阐述。

例：从某大学随机选取8名女大学生，其身高和体重数据如下表所示。求根据女大学生的身高预报体重的回归直线，并预报一名身高为172cm的女大学生的体重。

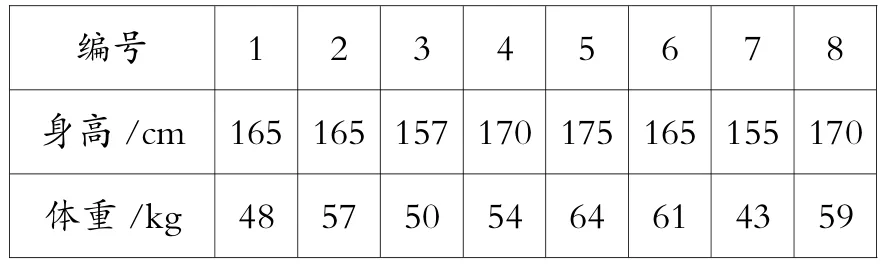
编号 1 2 3 4 5 6 7 8身高/cm 165 165 157 170 175 165 155 170体重/kg 48 57 50 54 64 61 43 59

教学时，我们可以这样操作：先将数据输入图形计算器中（如图1），再用图形计算器生成散点图（如图2），然后利用直线进行拟合生成回归直线（如图 3）。

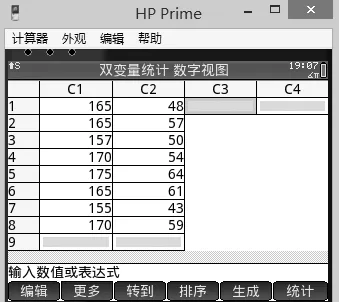
图1

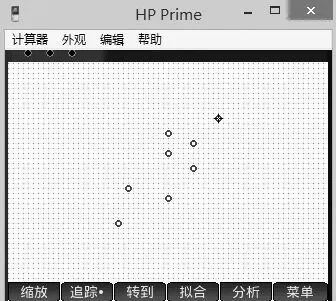
图2

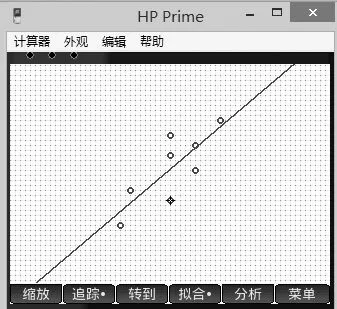
图3

这样我们就可以求出回归直线的方程y=0.894x-85.712，最后将172代入回归直线方程中，就得到身高172cm的女大学生体重的估计值。本案例如果利用传统方式进行教学，操作起来非常复杂。而借助图形计算器，为学生营造了探究学习的氛围，给学生提供了一个自主探究数学的机会，能很好地培养学生的思维能力。

二、对图形计算器应用于教学的思考

图形计算器具有很强的实用性和便捷性。合理地利用它可以给我们的教学带来便捷，提高学生学习数学的兴趣。但是，我们在使用图形计算器时也要注意一些问题。第一，不能过分地利用图形计算器。很多学生做题时往往都不进行独立思考，而是直接利用图形计算器进行解题。比如，在求解诸如函数值域或者最值之类的题目，学生直接用图形计算器进行绘图，然后得到函数的值域或最值，这样一来就完全违背了教学的初衷。图形计算器虽然有利于加深学生对数学知识的认识，但不能过分依赖，更不能替代学生的思考过程，所以教师在教学时一定要合理引导，切莫走偏。第二，教师应该不断提升自身的信息化水平。利用图形计算器进行教学是最近几年才兴起的，没有多少经验可借鉴，并且图形计算器更新换代的速度快，这就要求教师不断地去学习。如果教师在课前没有做好充分的准备，课堂教学时就难免出现措手不及的局面，以致影响教学效果。

长沙市周南中学）