基于模糊C-Means的改进型KNN分类算法

朱付保， 谢利杰， 汤萌萌， 朱颢东

(郑州轻工业学院 计算机与通信工程学院， 郑州 450002)

基于模糊C-Means的改进型KNN分类算法

朱付保， 谢利杰， 汤萌萌， 朱颢东*

(郑州轻工业学院 计算机与通信工程学院， 郑州 450002)

KNN算法是一种思想简单且容易实现的分类算法，但在训练集较大以及特征属性较多时候，其效率低、时间开销大.针对这一问题，论文提出了基于模糊C-means的改进型KNN分类算法，该算法在传统的KNN分类算法基础上引入了模糊C-means理论，通过对样本数据进行聚类处理，用形成的子簇代替该子簇所有的样本集，以减少训练集的数量，从而减少KNN分类过程的工作量、提高分类效率，使KNN算法更好地应用于数据挖掘.通过理论分析和实验结果表明，论文所提算法在面对较大数据时能有效提高算法的效率和精确性，满足处理数据的需求.

模糊C-Means； 聚类； KNN分类

随着信息时代的发展，存储能力的不断提升，数据增长的速度也日益加快.然而存储数据的结构也变得复杂多样，如何在有效的时间内完成数据的处理成为当前关注的问题之一.为了在数据产生后的有效时间内挖掘出隐藏的信息，实现信息的价值，因此在数据的处理速度方面有更高的要求.

数据挖掘中K最近邻(k-Nearest Neighbor，KNN)分类算法是一个理论上比较成熟的方法，也是数据分析和预测常用到的技术.在数据量较小的情况下，KNN分类算法能够快速有效的实现数据的分类.由于KNN需要存放所有的训练样本，不需要事先建立模型，有新样本需要分类时才创建，当数据量较大结构复杂时，算法的时间开销大，且精确度有所下降，因此运用KNN分类算法进行数据挖掘面临着困难.不少学者提出了改进的方法，闫永刚等提出了用MapReduce并行编程模型，同时结合KNN 算法自身的特点，给出了KNN 算法在Hadoop平台下的并行化实现，提高KNN算法处理大数据集的能力[1].刘应东、牛惠民等提出了提出一种基于聚类技术的小样本集KNN分类算法，算法通过进行聚类形成与各类样本密度相近的新样本集，在根据新样本集的特征对输入的未知样本对象进行分类标识[2].陈海彬、郭金玉等提出了，提出一种基于改进K-means 聚类的KNN 故障检测方法，其首先通过改进K-means 聚类将原始建模数据分成C个类，然后利用KNN 分别对每个类建立模型[3].罗贤锋、祝胜林等提出基于K-Medoids聚类的改进KNN算法为提高海量数据的分类效率，其利用K-Medoids算法对文本训练集进行聚类，分成相似度较高的簇，根据待分类文本与簇的相对位置，对文本训练集进行裁剪[4].这些方法对于KNN分类算法的执行效率及准确度都有很大提高.但是学者们对于模糊C-means降低KNN分类算法的复杂度研究的相对较少.KNN分类算法处理大样本数据效率会大大降低；当最近邻近分类器K很小时，其对数据噪音很敏感，分类的准确度降低，因此提出了基于模糊C-means的改进型KNN分类算法，通过C-means聚类算法对样本数据进行聚类处理，以减少数据分类的工作量，同时减弱无关属性对分类结果的干扰.

1 相关基础知识

1.1 KNN分类算法

K最近邻(k-Nearest Neighbor，KNN)分类算法，是一个理论上比较成熟的数据分类方法.

该方法的思路是：存在一个样本数据集合，也称为训练样本集，并且样本集中每个数据都存在标签，即事先知道样本集中每一数据与所属分类的对应关系.输入新的待分类的新样本数据时，新的样本数据的每个特征属性将和训练样本集数据集中的对应特征值进行比较，然后分类算法来提取样本集中特征最相似数据(最邻近)的分类标签.在进行分类时，大多情况只选择样本数据集的前K个相似度最高的数据，然后选择K个最相似数据集中出现次数最多的分类作为新的数据集分类.

KNN分类算法最初由Cover和Hart提出用于解决文本分类的问题[5].算法是为了将输入的测试数据点X分类为与该点最接近的K个邻近特征分类中出现最多的那个类别[6].K近邻算法是一种从测试数据点X开始，经过不断的扩展范围区域，一直把K个训练样本点都包含进去才停止，在归类的过程中，该算法会把测试样本点X归为距离最近的K个训练样本点中出现频率最大的类别.其中测试样本与训练样本的相似度一般使用欧式距离测量.

如果将K的取值固定下来，并且训练样本个数能够趋于无穷大，那么得到所有的K个邻近都将收敛于X.如同最近邻规则一样，K个近邻的标记都是随机变量，概率pwi|x，i=1，2，…，K都是相互独立的.假设pwm|x是较大的那个后验概率，那么根据贝叶斯分类规则，则选取类别wm.而最近邻规则是以概率pwm|x来选取类别，根据K近邻规则，只有当K个最近邻中的大多数的标记记为wm，才判定为类别wm[7-8].做出这样断定的概率为:

(1)

通常K值越大，选择类别wm概率也越大.

1.2 模糊C-means聚类算法

传统聚类分析算法把待识别的样本对象严格的划分到对应的类中，只有“是或否”两种归类，按这种算法划分的界限是分明的.但是对于现实应用中，其样本属性并没有严格的属性，它们在形态和属性等方面存在中介性，可能同时满足两种对立的特性，因此传统的聚类分析算法无法解决这类问题.

为了更好的解决聚类问题，Dunn利用Ruspini提出的模糊划分的概念，将其推广应用到了模糊聚类上，后来Bezdek又将Dunn的工作推广到基于模糊度m的一般C-means形式，提出了模糊C均值聚类(FCM)，这是一种根据传统的聚类的改进算法，其目标函数定义如同C-means聚类算法，该算法基于数据样本集的隶属度，不同于传统的聚类严格的把样本单纯的归于某一类中.但是其权重矩阵W不在是二元矩阵，而是应用了模糊理论的概念，以其归属程度表示属于各聚类的程度.

模糊C-means聚类把n个样本集合Xi(i=1，2，3，…，n)分成对应的k个模糊组，计算出各组对应的聚类中心，使按价值函数求出的非相似性系数最小.模糊C-means聚类算法引用了模糊划分的概念，为了确定其属于各个组的程度，要求算法给每个样本数据点用0到1之间的值来表示隶属度[9-10].但是一个数据样本集的隶属度总和相加等于1.

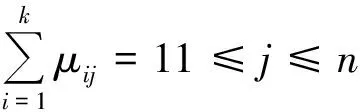
(2)

其中，模糊C-means聚类的样本集合Xi(i=1，2，3，…，n)目标函数公式为：

(3)

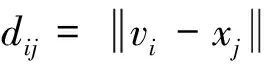
模糊C-means聚类算法的具体实现步骤如下：

1)首先用[0，1]间的随机数来初始化样本集的隶属度，生成隶属矩阵M，使其满足隶属度总和相加等于1的条件.

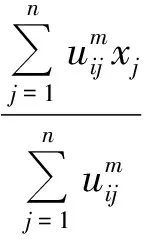
3)根据价值函数公式计算出其对应的价值函数.如果计算出的价值函数小于规定的阈值或者相对上次价值函数值的改变量小于某个阀值，则算法停止[11-13].

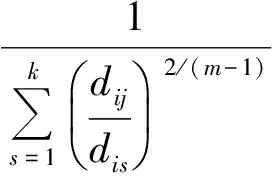
2 本文所提算法

2.1 算法基本思想

首先把样本集合经过处理分成对应的K个模糊分组，其分组的理论是根据样本集的隶属度为依据，将其中的模糊子集A中的所有样本X，为其定义一个数值μA(x)∈[0，1]来作为样本X对A集合的隶属度，从而来确定聚类分组的数目，再根据划分的组进一步确定每个分组对应的聚类中心vi(i=1，…，k)，进而初始化加权指数m.其次根据聚类处理后形成的子簇数据分类，在子簇数据中按照KNN算法，在子簇集合中找出与测试样本相对接近的所有样本集合，然后根据得到的最邻近列表样本的多数类进行分类.

算法的实现基本流程图如图1所示.

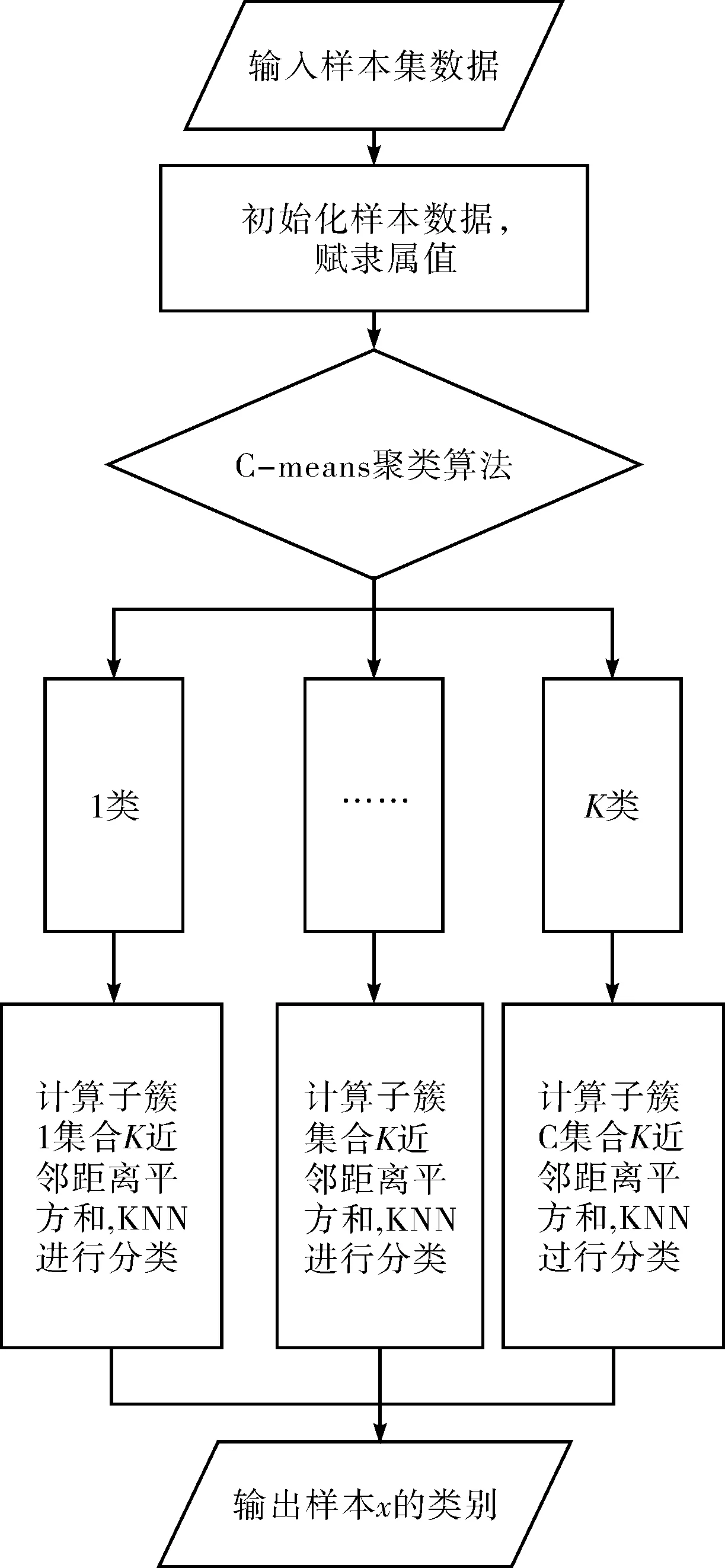
图1 本文算法流程图Fig.1 Flow chart of the proposed algorithm

2.2 算法具体描述

根据模糊分组理论，本文算法具体描述如下：

输入：样本集D=x1，x2，…，xn，其x1，x2，…，xn为样本集D的属性集，C=c1，c2，…，cm是簇数为K的类别属性.

输出：样本属性值x的所属类别号.

1) 待分类的样本集x1，x2，…，xn进行初始化，其中∀xi∈R1≤i≤n，设置分类的种类数值为k，即划分成k个模糊分组.设置样本集xi的隶属度，满足所有样本的隶属度(权重)的和为1，生成隶属矩阵M.

2) 根据模糊聚类中心求解公式，求出各个分组的中心点vi(i=1，…，k).

3) 根据价值函数公式计算出其对应的价值函数，判断是否收敛，如果不满足收敛条件则重新构造出新的矩阵M，再返回2).

4) 根据划分的分组形成的子簇来代替该子簇的样本集合，对子簇中的样本用x，y的形式表示，则具有n个属性的样本为x1，x2…xn，y，y是样本的类标号.

5) 依次计算出每个测试样本t=x'，y'与每个训练样本x，y之间的距离d.

6) 按照距离的递增依次排序.

7) 取出与测试样本点距离最小的k个点.

8) 根据取出的点，确定这K个点所在类别出现的频率.

9) 根据计算的频率值，返回K个点中频率最高的类别作为当前点的预测分类.

3 实验对比与分析

为了验证文中改进算法的有效性，以某房地产公司2012年至2016年房屋销售管理的数据为例进行实验对比，其中数据包含客户信息、房屋信息、销售人员信息等.实验的硬件环境为Intel i7处理器，主频为3.6 GHz，内存为 4 GB；实验的软件环境为Microsoft Windows 7 操作系统，Microsoft SQL Server 2005数据库，Eclipse Luna 4.4.2，jdk7.0；算法实现的语言为java.

本文实验主要选取房地产公司2012年～2016年销售信息作为实验的数据集合.各数据集的详细信息如表1和表2所示.

表1 实验数据集

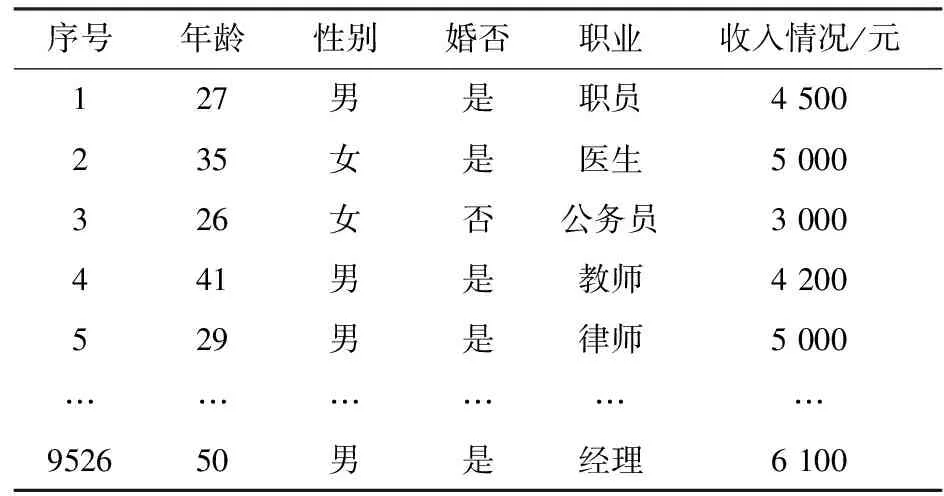
表2 部分客户信息

为验证改进算法的有效性，实验设计了两组实验进行对比.本实验选取基于K-means的KNN分类算法、基于K-Medoids的KNN算法和本文改进算法(基于模糊C-means的KNN分类算法)作比较.本文为改进算法了实现数据的分类，根据需要分类数据的业务背景，简化实验复杂度，设定了实验K值为定值2(是否购买)，用以分类来预测访客户购房行为.算法的性能评估从算法的执行效率和分类结果的准确度两个方面来衡量，执行效率方面比较两种算法在同一实验环境下处理同一组数据集的时间.

第一组实验选取了数据集最大的2015年作为数据模型.对2015年的数据集实验测试结果对比如图2和图3所示.

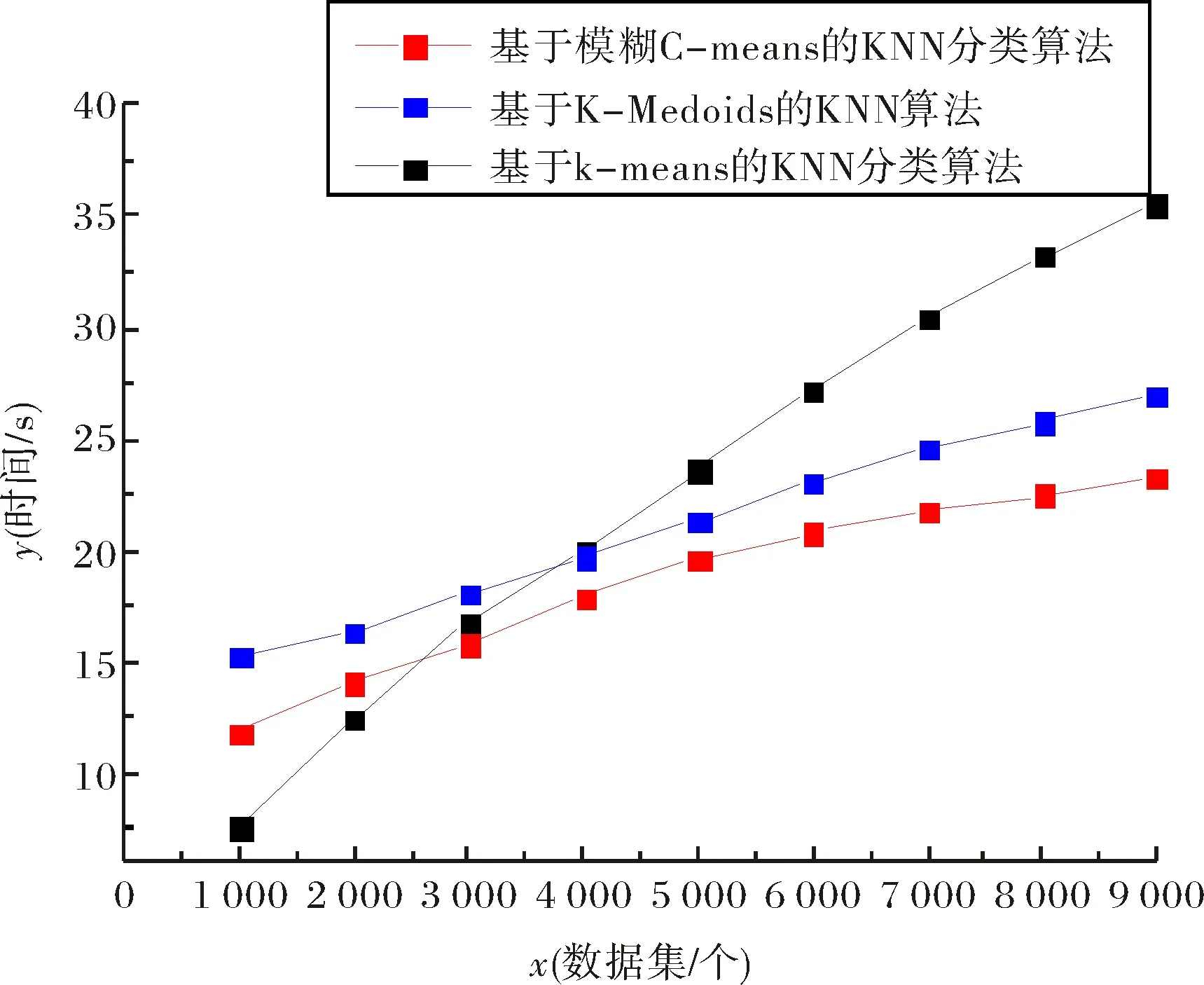
图2 各算法在2015年数据集上的运行时间比较结果Fig.2 Comparative results of the running time of algorithms on the 2015 data set

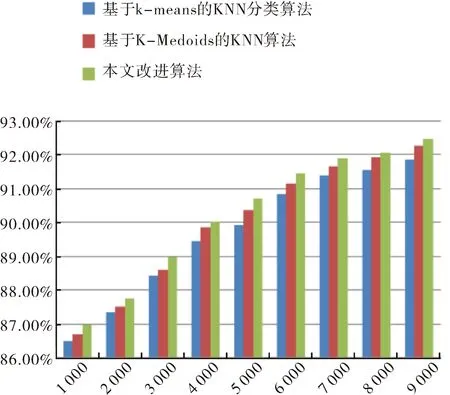
图3 各算法在2015年的数据集上的分类准确度比较结果Fig.3 Comparative results of the classification accuracy of algorithms on the 2015 data set

第二组实验使用了2012年～2016年的全部数据集.在各个数据集上进行分类算法的对比实验测试结果如表3.

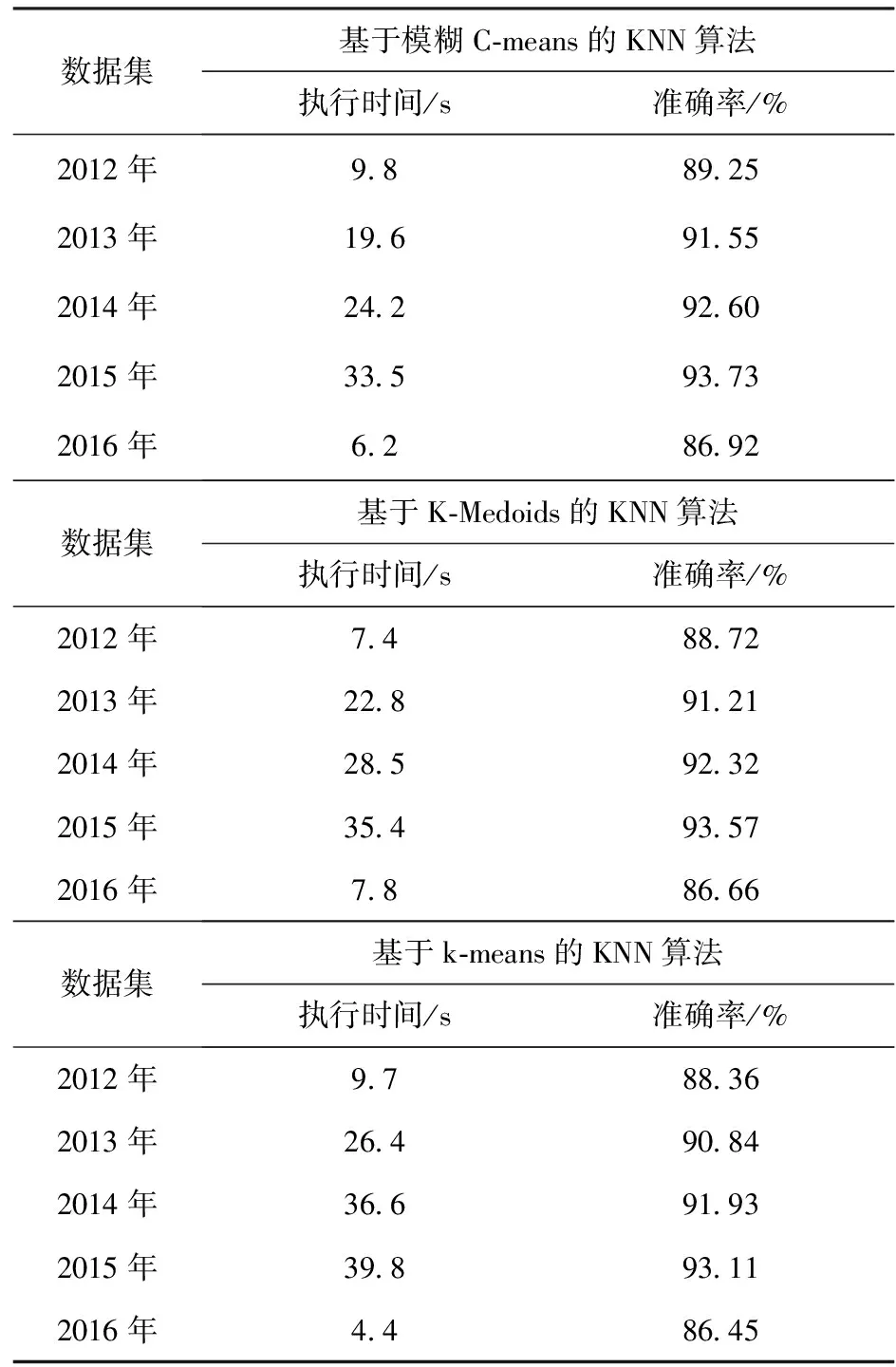
表3 实验测试结果

根据上述对5组数据分别用两种算法测试，其对比结果如图4和图5所示.

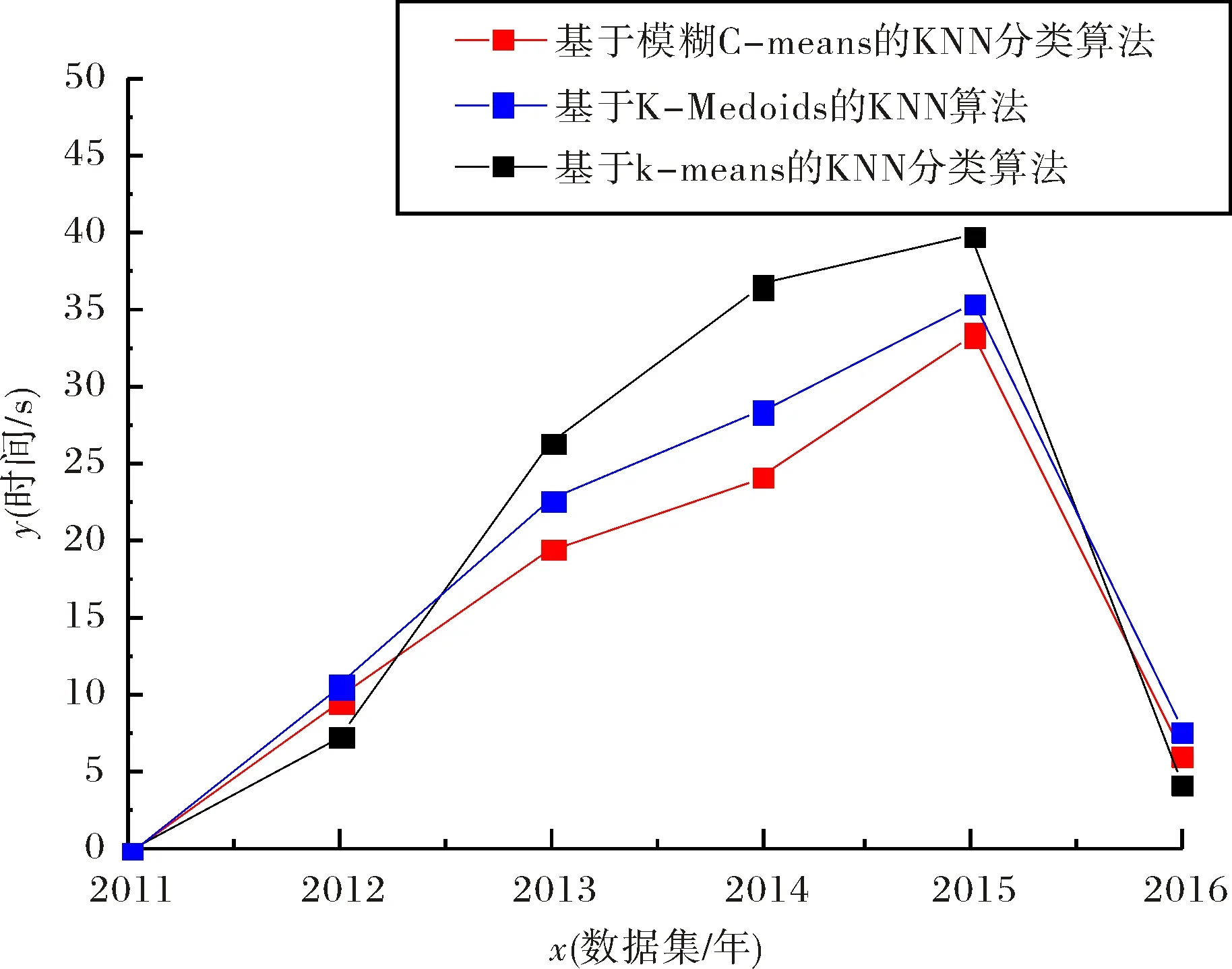
图4 各算法在各数据集上的运行时间比较结果Fig.4 Comparative results of the running time of algorithms on the data sets

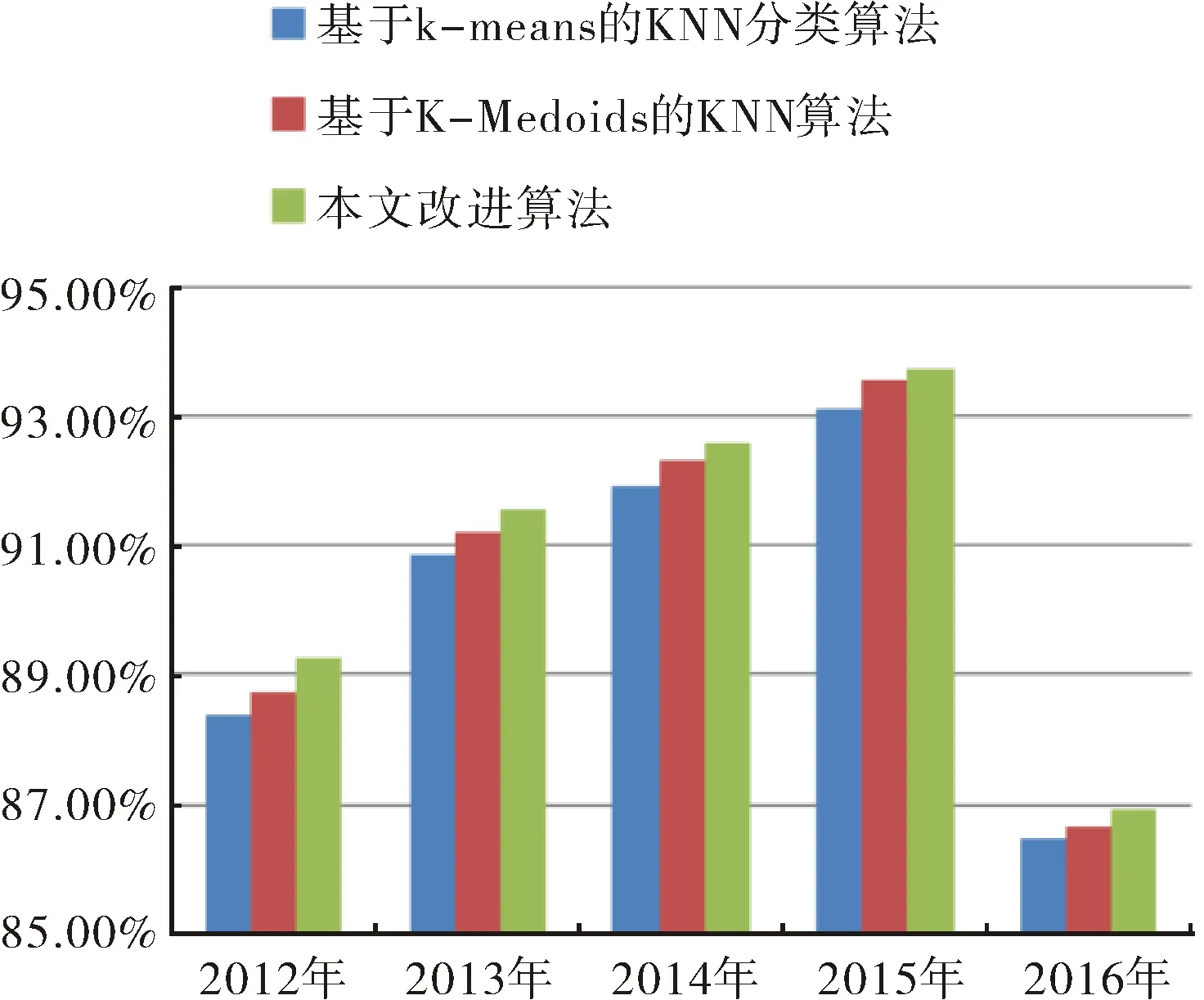
图5 各算法在各数据集上的分类准确度比较结果Fig.5 Comparative results of the classification accuracy of algorithms on the data sets

本文改进算法与基于K-means的KNN分类算法、基于K-Medoids的KNN算法相比，其主要区别在于本文算法融入了模糊分组理论，使得每一个输入的样本数据不再仅隶属于特定的聚类，而是以其隶属程度来表示，对样本集进行聚类，减少分类过程中的算法的计算量，提高了算法执行的效率，充分的发挥了该算法处理大样本集、高维度数据的优势.

从图2～图5中的实验对比结果来看，对于第一组实验采用2015年数据集，随着实验样本量的增大，本文提出的改进算法比基于K-means的KNN分类算法、基于K-Medoids的KNN算法执行效率和分类的准确率高.对第二组实验用了2012年至2016年的五个数据集，本文提出的改进算法在执行效率方面大都略优于其他两种分类算法，同样在分类的准确率方面也高.但对于小样本集，如第一组实验中的小样本集和第二组实验中的2016年数据集，本算法所执行的效率略低于基于K-means的KNN分类算法，主要是由于本文算法在执行的过程中进行模糊分组聚类需要耗费一部分时间，在样本量小的情况下，虽然能够减少分类样本的数据量，但是这种时间的减少在整体效果上体现不明显，另一方面改进算法准确率高于基于K-means的KNN分类算法.对于2015年的较大数据集处理上，本算法不仅能在准确率上有所提高，而且在执行分类能力方面高于基于K-means的KNN分类算法.结果表明，相同条件下，基于模糊C-means的KNN分类算法比基于K-means的KNN分类算法运行时间短，在执行大样本集分类时效率方面优于基于K-means的KNN分类算法，且算法分类准确率更高；本文改进后的算法与基于K-Medoids的KNN算法相比较执行效率略高，由于基于K-Medoids的KNN算法需要得逐步计算直到类收敛，消耗一部分时间.通过两组实验对比，本文提出的改进算法对比之前两种算法在分类性能均有所提高.

4 结束语

本文针对KNN分类算法在处理数据量大、维度高的样本效率低的问题，提出了一种基于模糊C-means的KNN分类算法，利用样本集隶属程度的特性，对样本集进行聚类，然后根据聚类形成的子簇来代替该子簇的所有样本集，从而减少对样本集进行分类处理的数据量，提高算法的运算效率.通过对不同的数据集进行测试表明，本文提出的算法有利于提高大样本集的分类的效率，降低运算时间的消耗，同时也提高了分类结果的准确率.

[1] 闫永刚， 马廷淮， 王 建. KNN分类算法的MapReduce并行化实现[J]. 南京航空航天大学学报， 2013，45(4):550-555．

[2] 刘应东， 牛惠民. 基于k-最近邻图的小样本KNN分类算法[J]. 计算机工程， 2011，37(9):198-200．

[3] 陈海彬， 郭金玉， 谢彦红. 基于改进K-means聚类的kNN故障检测研究[J]. 沈阳化工大学学报， 2013，27(1):69-73．

[4] 罗贤锋， 祝胜林， 陈泽健， 等. 基于K-Medoids聚类的改进KNN文本分类算法[J]. 计算机工程与设计， 2014，35(11):3864-3867,3937．

[5] 耿丽娟， 李星毅. 用于大数据分类的KNN算法研究[J]. 计算机应用研究， 2014，31(5):1342-1344,1373．

[6] BHATTACHARYA G， GHOSH K， CHOWDHURY A S. An affinity-based new local distance function and similarity measure for KNN algorithm [J]. Pattern Recognition Letters， 2012，33(3):356-363．

[7] SU M Y. Using clustering to improve the KNN-based classifiers for online anomaly network traffic identification [J]. Journal of Network & Computer Applications， 2011，34(2):722-730．

[8] 夏竹青. 基于不均衡数据集和决策树的入侵检测分类算法的研究[D]. 安徽:合肥工业大学， 2010．

[9] GAO Y， GAO F. Edited AdaBoost by weighted kNN [J]. Neurocomputing， 2010，73(18):3079-3088．

[10] 王永贵， 李鸿绪， 宋 晓. MapReduce模型下的模糊C均值算法研究[J]. 计算机工程， 2014，40(10):47-51．

[11] 文传军， 汪庆淼， 詹永照. 均衡模糊C均值聚类算法[J]. 计算机科学， 2014，41(8):250-253．

[12] 周世波， 徐维祥， 柴 田. 基于数据加权策略的模糊C均值聚类算法[J]. 系统工程与电子技术， 2014，36(11):2314-2319．

[13] HAVENS T C， BEZDEK J C， LECKIE C， et al. Fuzzy C-means algorithms for very large data [J]. IEEE Transactions on Fuzzy Systems， 2012，20(6):1130-1146．

ImprovedKNNclassificationalgorithmbasedonFuzzyC-Means

ZHU Fubao, XIE Lijie, TANG Mengmeng, ZHU Haodong

(School of Computer and Communication Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China)

KNN algorithm is a classification algorithm that is simple and easy to implement, but when the training set is rather big and features are more, its efficiency is low with which takes more time. To solve this problem, an improved KNN classification algorithm was proposed based on Fuzzy C-Means. The improved algorithm introduces the theory of Fuzzy C-Means based on the traditional KNN classification algorithm. Through processing the sample data clustering, the formation of sub clusters substitutes all the sample set of the sub cluster, which helps reduce the number of training set. Thereby the workload of the KNN classification process is reduced, with the classification efficiency improved and the KNN algorithm better applied in data mining. The theoretical analysis and experimental results show that this method is able to significantly improve the efficiency and accuracy of the algorithm when dealing with large data, meeting the demand of processing data.

Fuzzy C-Means; clustering; KNN classification

2017-02-22.

河南省科技攻关项目(162102210146；162102310579);河南省教育厅科学技术研究重点项目(13A52036); 河南省高等学校青年骨干教师资助计划项目(2014GGJS-084); 郑州轻工业学院校级青年骨干教师培养对象资助计划项目(XGGJS02); 郑州轻工业学院博士科研基金资助项目(2010BSJJ038).

*通讯联系人. E-mail: zhuhaodong80@163.com．

10.19603/j.cnki.1000-1190.2017.06.005

1000-1190(2017)06-0754-06

TP311.13

A