我国网上拍卖竞买者出价行为特征分析
曹珂+严明义
摘要:近年来,如何从个人角度分析竞买者出价行为成为研究难点。本文运用基于函数性稀疏数据聚类方法从竞买者个人角度定义了基于条件期望的距离矩阵,并结合多维尺度分析方法(MDS)和相平面图分析法对竞买者出价行为特征进行聚类分析。结果表明,按出价时间、金额、出价能量以及获胜概率可将竞买者分为显著的四类。其中,经验丰富型竞买者获胜概率最高,势在必得型竞买者获胜意愿最强烈,缺乏经验型竞买者退出竞拍时间较早导致获胜概率较低,围观型竞买者由于竞拍意愿不强烈所以获胜概率最低。
关键词:稀疏数据;函数性聚类分析;出价行为特征;网上拍卖
文献标识码:A文章编号:100228482017(06)011507
一、 引言
近十年来,不论是国外的eBay、Amazon,抑或是中国的淘宝网拍卖会、嘉德在线等网上拍卖平台发展迅速,吸引了大量竞买者参与。同时,网上拍卖种类也日臻完善,艺术品、司法拍卖等特殊品拍卖也逐渐采用以网上拍卖为主的销售渠道。网上拍卖的普及一方面节省了组织者的人力、物力成本,另一方面也降低了竞买者的参与门槛,使资金量较少的普通竞买者也能参与其中,增加竞买人数,竞拍更加激烈,带来双赢结果。
对传统线下拍卖理论的研究始于1961年,Vickrey[1]假设竞买者价值独立分布且对称(服从同一分布函数)、风险中性并无预算约束,通过对比四种基本拍卖方式(英式拍卖、荷兰式拍卖、第一价格密封拍卖、第二价格密封拍卖)下的买卖双方收益与竞拍效率,得出收益等价原理,这一原理构成了私人价值拍卖理论的基准。后续大量研究在此基准上对限定性条件加以推广,将相关竞买者假设逐一放松,以博弈论为工具探讨不同拍卖方式对收益等价原理的影响。其实早在1961年Vickrey就指出竞买者之间存在的不对称性,并对比了两个不对称竞买者参与的不同拍卖方式下的收益情况。他假设竞买者1的价值为共同知识,竞买者2的价值则服从[0,1]的均匀分布,则第一价格密封拍卖的收益可能高于也可能低于第二价格密封拍卖的收益。在应用方面,Marshall et al.[2]提出了计算不对称拍卖中竞标策略收益的几种数值算法。Maskin & Riley[3]则具体研究了不对称第一价格密封拍卖下的均衡性质,认为当竞买者不对称时,通过第一价格拍卖获得的期望收益可能超过第二价格拍卖中的期望收益。可以看到,由于传统拍卖行业具有专业性强、资金需求量大等特点,使得竞拍参与者具有较高同质性,早期拍卖理论研究中的竞买者对称性假设与线下真实竞拍参与者属性相吻合。后续研究尽管放宽了竞买者对称性假设,但研究重点关注于不同拍卖方式下收益、效率比较而较少从竞买者非对称性出发,从个人角度对竞买者真实出价行为进行分析。
网上拍卖的兴起降低了搜索成本,克服了空间与时间的限制,交易品种不再局限于高价值物品,拓宽了竞拍参与者的广度,传统拍卖理论中对竞买者对称性假设不再符合实际。同时,大量的网上交易数据也为研究网上拍卖中竞买者出价行为提供了便利。在网上拍卖竞买者出价行为的研究中,一些学者通过对竞买者出价行为分类,寻求不同竞买者的出价规律,辨析不同出价行为之间的差异。Hayne[4]是開创这一研究领域的先行者。他随机搜集了eBay网中不同类别下的出价数据,按出价次数和出价时间将竞买者分为两大类和六小类,分别是:单次出价者(早出价、中期出价、晚出价)和多次出价者(初次出价、探查式出价(Probe Bid)、哨兵式出价(Sentry Bid)),其中,单次晚出价的成交成功率最高,单次早出价的成功率最低。Bapna[5]在Hayne的研究基础上,将出价时间细分为进入拍卖时间(Time of Entry)和退出拍卖时间(Time of Exit),并结合出价次数共三个指标运用快速聚类法(kmeans聚类法)将网上Yankee拍卖中的竞买者分为显著的五类:早出价者(Early Evaluators)、中期出价者(Middle Evaluators)、机会主义者(opportunists)、全程参与出价者(Participators)以及浅尝辄止者(SipandDippers)。Bapna同样也研究了不同出价行为下的获胜概率,利用单因素方差分析检验不同出价策略是否具有相似的获胜概率,结果显示机会主义者和浅尝辄止者的获胜概率远高于其余三类竞买者。
由于出价数据的不等时间间隔造成早期网上拍卖研究大多只能通过离散的出价金额分析竞买者出价行为。在Ramsay和Silverman[6]系统性地引入函数性数据分析方法后,越来越多的学者通过观测到的离散出价数据背后的潜在价格轨迹来研究竞买者网上出价行为。Shmueli & Jank[7],Shmueli & Russo[8],Jank & Shmueli[9]以函数性主成分分析为基础,运用曲线聚类方法对不同拍品的价格轨迹进行聚类,探究网上拍卖价格形成过程中的异质性并寻找影响出价的动因来源。严明义[10]通过对中国淘宝网珠宝类拍卖的出价数据运用基于基函数的函数性聚类分析方法,发现拍品的价格等级和类别会对竞买者的出价行为产生不同影响。
通过对现有文献回顾可知,网上拍卖竞买者出价行为研究以函数性数据分析方法的引入为界限可分为早期研究和现有研究。早期研究多采用传统的计量统计方法,通过离散的出价数据分析竞买者出价行为,聚类指标体系相对单一;现有研究则运用函数性数据分析方法拟合不同拍品在整个拍卖期间连续平滑的出价轨迹,研究不同拍卖属性对竞买者出价行为的影响,但较少从竞买者个人角度出发,研究非对称竞买者在整个拍卖期间的出价行为特征。因为若从竞买者个人角度出发,单一竞买者在整场拍卖中的出价数据具有稀疏性和不等间隔分布性,无法通过插值或修匀来获得平滑的出价轨迹,造成大量的稀疏序列被人为剔除,得到的研究结论并不严谨,如何分析稀疏且不等间隔时间分布的出价序列为函数性数据研究带来了挑战。endprint
单个竞买者的一次出价序列实际上是一条潜在连续出价轨迹中的部分点,对应着一个随机过程的实现,反映了竞买者的出价行为变化。本文从随机过程角度利用R软件和MATLAB编写程序,运用函数性稀疏数据聚类分析方法对从淘宝网多物品拍卖中的竞买者出价轨迹进行聚类,并结合不同类中竞买者在整个拍卖期间的出价金额、出价时间、相平面图以及最终获胜情况刻画我国网上拍卖竞买者的出价行为特征,试图寻求不同类竞买者出价行为的差异与共性,这对提高竞买者出价效率、减少盲从出价以及完善拍卖网站交易规则设计具有重要意义。二、 函数性稀疏数据聚类分析方法
聚类分析的目的是将目标对象分类,使得同一类对象的相似性大于类与类之间的相似性。因此,首先需要确定如何度量对象之间的相似性或相异性。与经典多元统计中的聚类分析类似,函数性聚类分析的首要工作同样通过定义距离来获得相异性矩阵,一旦构建了一个合理的距离,我们就可以根据该距离矩阵对目标对象进行聚类。但是由于拍卖出价数据到来时间的不等间隔性以及稀疏性,我们考虑采用基于真实出价序列的条件期望距离来反映不同出价轨迹间差异。
(一)模型设定
设实际观测到的出价数据{yil:1≤l≤ni;1≤i≤N}(ni通常很小)是函数{xi(t):t∈T;1≤i≤N}在t=til处的观测值。由于观测数据往往带有观测误差,因此函数性数据分析的基本统计模型为:
yil=xi(til)+εil1≤l≤ni,1≤i≤N(1)
其中εil为第i个竞买者的第l次观测的随机误差,E(εil)=0,var(εil)=σ2。
xi(t)(i=1,2,…,N)为定义在闭区间[a,b]上的平方可积随机过程{x(t),t∈T}的N次实现,则存在半正定核C(·,·)满足cov(x(s),x(t))=C(s,t)。于是,利用核C(·,·)的特征函数可得到xi(t)的扩展式:
xi(t)=μ(t)+∑∞k=1zikθk(t)(2)
其中μ(t)为x(t)的均值函数;{zik,k≥1}的均值为0,方差为λk且不相关,λ1≥λ2≥…≥0是核C(·,·)的特征值且∑∞k=1λk<∞;θ(·)为特征值对应的正交特征函数。
则模型(1)可以看作是由随机过程x(t)的稀有带噪音的实现构成,即真实出价轨迹可用平滑出价轨迹附加扰动项的形式来表示。此类稀疏数据的相异性可采用L2距离进行度量。令
D(i,j)=∫ba(xi(t)-xj(t)2dt)1/2
考虑到单一竞买者出价观测时点的稀疏且不规律性,上式难以计算。设Yi=(yi1,yi2,…,yini)′,Yj=(yj1,yj2,…,yjnj)′,得到基于已知的观测到的真实稀疏数据序列Yi和Yj的条件期望距离:
(i,j)={E[D(i,j)2Yi,Yj]}1/2
1≤i,j≤N
将式(2)代入上式可得:
2(i,j)=E∑∞k=1(zik-zjk)2Yi,Yj
则对任意正整数K,(i,j)有如下截断形式
(K)(i,j)=E∑Kk=1(zik-zjk)2Yi,Yj1/2=
∑Kk=1var(zikYi)+var(zjkYj)+
[E(zikYi)-E(zjkYj)]21/2(3)
可知
E[(K)(i,j)2]=∑Kk=12λk=E[D(K)(i,j)2]
即(m)(i,j)2是所需估計平方L2距离的无偏估计量,这样一来,可通过估计条件期望距离得到对不同竞买者出价轨迹相异性的度量。
(二)参数估计
由上述分析可知,条件期望距离可通过求解E(zikYi)和var(zikYi)获得。下面我们将说明如何估计截断形式的(K)(i,j)。对于任意的正整数K≥1,在1≤i≤N、1≤k≤K下,设Λ(K)为对角线上元素为(λ1,…,λK)的K×K阶对角矩阵。μi=(μ(ti1),…,μ(tini))′和Z(K)i=(zi1,…,ziK)′分别为x(t)的均值函数和特征值函数组成的向量,θik=(θk(ti1),…,θk(tini))′为x(t)特征函数组成的向量且Θ(K)i=(θi1,…,θiK)。为方便后续研究,假设xi、yi均为正态随机过程,即zik~N(0,λk),εij~i.i.dN(0,σ2),则Yi~N(μi,ΣYi),Z(K)i~N(0,Λ(K)),其中ΣYi=cov(Yi,Yi)。又cov(Z(K)i,Yi)=E(Z(K)iYi)=Λ(K)(Θ(K)i)′,则Yi和Z(K)i的联合分布[11]为:
Yi
ZKi~Nμi
0,ΣYi,Θ(K)iΛ(K)
Λ(K)(Θ(K)i)′,Λ(K)
可知:
E(Z(K)iYi)=Λ(K)(Θ(K)i)′Σ-1Yi(Yi-μi)(4)
var(Z(K)iYi)=Λ(K)-Λ(K)(Θ(K)i)′Σ-1YiΘ(K)iΛ(K)(5)
将式(4)、(5)分别带入式(3)可得:
((K)(i,j))2=
tr[Λ(K)-Λ(K)(Θ(K)i)′Σ-1YiΘ(K)iΛ(K)]+
tr[Λ(K)-Λ(K)(Θ(K)j)′Σ-1YjΘ(K)jΛ(K)]+
[tr(Λ(K)(Θ(K)i)′Σ-1Yi(Yi-μi))-
tr(Λ(K)(Θ(K)j)′Σ-1Yj(Yj-μj))]2
这样,通过估计出价轨迹Yi的均值曲线μ(·)、协方差函数的前K个特征值{λk,k=1,…,K}所对应的特征函数{θk,k=1,…,K}以及误差方差σ2可获得条件期望距离。endprint
在获得反映不同竞买者出价轨迹间差异的距离矩阵后,便可对距离矩阵应用聚类法分类。在确定合理分类数目时,我们通过计算不同分类数下的SSE值和轮廓系数[12](Silhouette Coefficient),最终区别出四类明显的竞买者出价行为,并应用多维尺度变换分析(MDS)将原距离矩阵映射到二维空间,使分类后的结果可视化。三、 基于稀疏函数性聚类方法的竞买者
出价行为的实证分析目前国内较大的拍卖网站有淘宝拍卖会、嘉德在线、淮海在线等,均以艺术品拍卖为主。与普通商品相比,艺术品交易频率低、市场流动性差、价格波动较大,通过拍卖确定艺术品价格是一种十分普遍且有效的定价方式。在数据搜集阶段发现,嘉德在线、淮海在线等网站的拍卖品多为价格波动大的私人书画作品且日均出价数较少。而eBay为了增加竞拍的激烈程度,现仅提供拍卖实时报价折线图,并没有确切的出价时间,也无法在拍卖结束后获得竞拍历史数据。淘宝拍卖会则全部采用多物品同时竞拍模式(拍卖专场),竞拍时间限定在一天之内,竞买者可同时参与竞拍多件物品,全年的历史拍卖数据均可获得。基于此,考虑到数据的可获得性和真实稳定性,本文利用爬虫软件搜集到淘宝拍卖会2015年第三季度(7月至9月)紫砂壶拍卖专场的全部出价数据。拍卖方式为英式拍卖,共计223件拍品。由于存在延迟出价机制,平均拍卖时长为12小时53分,起拍时间均为上午10时。此外,网站还提供代理出价选项帮助竞买者参与竞拍。
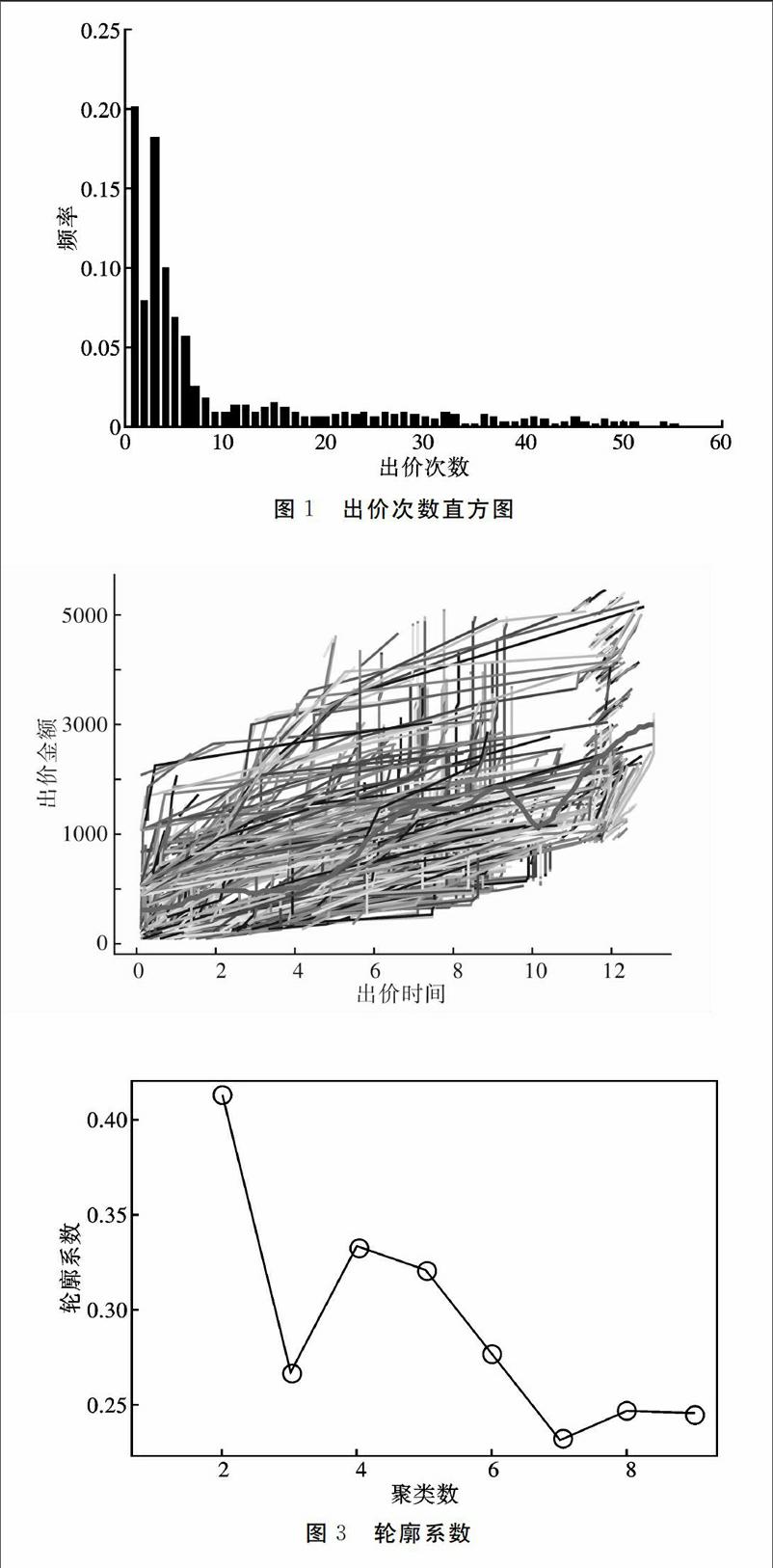
在剔除异常值后得到1134位竞买者参与的223件拍品的1978条出价轨迹,共计出价次数13726次。从出价次数频率图1可以看到, 20%的竞买者出价仅为一次出价,大多数竞买者在一场拍卖中的出价次数为一至四次,占全部出价次数的50%以上,说明大多数竞买者的出价时间分布稀疏且不规律。图2为所有竞买者的出价轨迹图,其中粗线代表平均出价轨迹。观察图2可知,一部分竞买者并没有在整个拍卖期间持续出价,而是在拍卖
末期形成了类似“小线段”的出价轨迹,这也同样证实了拍卖出价数据到来时间的稀疏性和不规律性。
在剔除设定起拍价的竞买者出价后,通过R软件编程估计出真实出价轨迹Yi的均值曲线、协方差平面以及误差方差。在估计条件距离时,本文选择协方差核函数的前十个特征值,占到随机轨迹总变差的9128%。在得到距离矩阵后,运用MATLAB中的mdscle函数对距离矩阵进行多维尺度分析,将原距离矩阵映射到2维空间中①。在选择聚类数时,运用MATLAB编程计算2到8类下的轮廓系数,得到图3并选择聚类数下较大的轮廓系数,确定将竞买者分为四类②。最后运用Kmeans聚类法对距离矩阵进行聚类,得到四类竞买者的二维空间匹配图4。
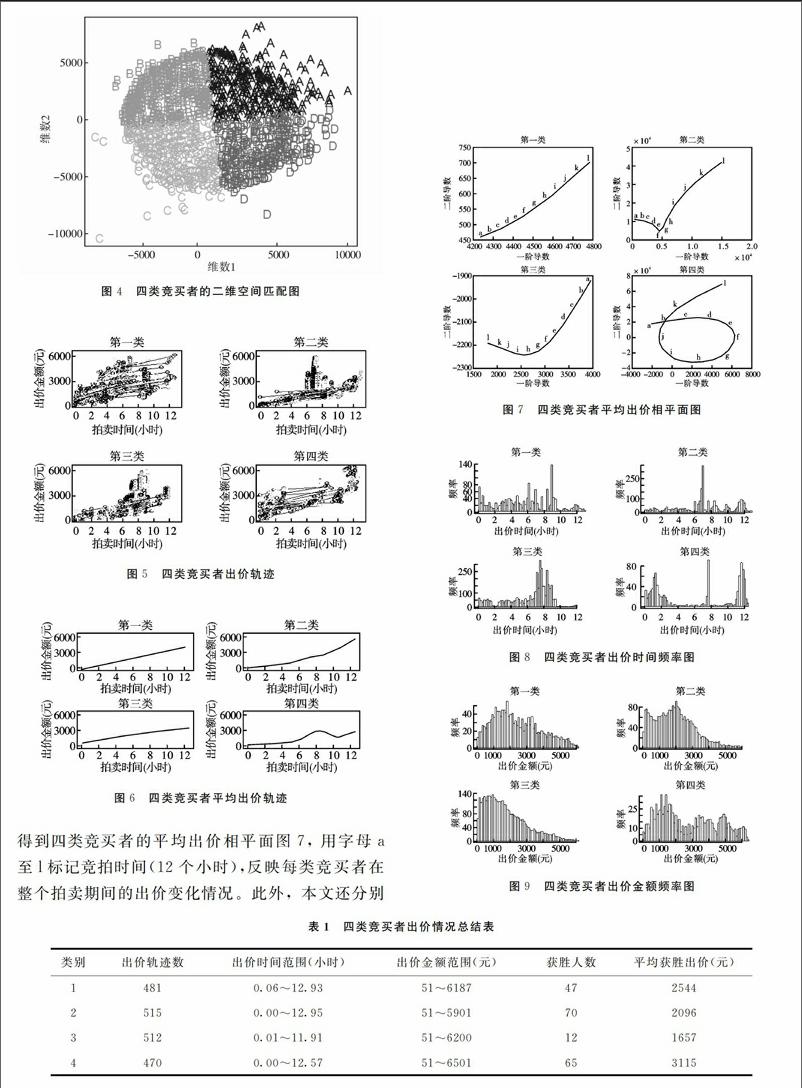
为了便于观察,分别用“A”“B”“C”“D”代表第一类至第四类竞买者,并绘制四类竞买者的出价轨迹图5以及平均出价轨迹图6。根据平均出价轨迹
①mdscale函数提供了四种度量拟合准侧,仅在sammon准则下stress值达到最小且小于10%(0.0748),达到克鲁斯卡尔提出的经验标准(≤10%),说明模型对数据的拟合程度为满意(Fair)。
②轮廓系数(Silhouette Coefficient)结合了聚类的凝聚度(Cohesion)和分離度(Separation),用于评估聚类的效果。该值处于-1~1之间,值越大,表示聚类效果越好。由轮廓系数图可知,当K=4时轮廓系数最大,故将竞买者出价分为四类。图4四类竞买者的二维空间匹配图
得到四类竞买者的平均出价相平面图7, 用字母a至l标记竞拍时间(12个小时),反映每类竞买者在整个拍卖期间的出价变化情况。此外,本文还分别绘制了各类竞买者的出价时间频率图8以及出价金额频率图9。最后,总结不同类竞买者的基本出价情况,主要包括出价轨迹数、出价时间范围、出价金额范围、平均获胜金额以及获胜人数,如表1所示。
四、 竞买者出价行为特征的聚类分析
通常情况下,一场拍卖的早期和晚期会比中期吸引更多的竞买者参与。在拍卖末期的疯狂出价被称为拍卖狙击,是由竞买者强烈希望赢得拍品所产生的。除了希望赢得拍品,一些竞买者参与竞拍的主要目的是希望以尽可能低的出价赢得拍品。对竞买者出价轨迹进行分类就可以区别不同类竞买者的出价行为特征、鉴别不同的出价策略,研究不同出价策略的有效性,探讨竞买者参与竞拍的目的是最大可能赢得物品还是以最合理的低价拍得物品。所以,在得到全部竞买者出价行为的四个分类后,从获胜概率切入,结合出价时间、出价金额、平均出价相平面图分别对各类竞买者进行描述,希望寻求不同类竞买者出价行为之间的差异与共性。
由获胜概率可知,第二类竞买者获胜概率最高,其次为第四类竞买者,随后是第一类竞买者,获胜概率最低的是第三类竞买者。第二类竞买者参与竞拍时间最长,但很少会选择在拍卖前期就出价竞拍,他们往往会先熟悉拍品并观察其他竞买者的出价行为,所以该类竞买者多偏好在拍卖中后期出价,且出价金额并不高,多集中在[0-3000]元的低档,并不会为了赢得物品而在拍卖后期盲目竞拍高价,属于有一定竞拍经验的参与者。从其相平面图看,该类竞买者平均出价水平的一阶导数和二阶导数均大于绝对零点,出价能量在拍卖中前期有递减的趋势,但在拍卖中后期则逐渐远离绝对零点,出价波动在拍卖中后期最为剧烈。
第四类竞买者与第二类竞买者同样偏爱在拍卖中后期出价。不同之处在于该类竞买者会更多选择在拍卖初期,尤其是拍卖末期参与竞拍,且平均出价金额在四类中最高。可见该类竞买者参与竞拍的目的不是以相对合理价格赢得拍品,而是以最大概率拍得物品,竞拍意愿强烈,以至于该类竞拍者会在拍卖末期出现明显的拍卖狙击行为,从而拥有较高的获胜概率,但最终成交价格会大幅攀升。同样从相平面图来看,该类竞买者平均出价水平的一阶导数和二阶导数在拍卖初期逐渐接近绝对零点,而在拍卖后期末期的远离绝对零点,并且出价能量在拍卖末期达到最大,说明在整个拍卖期间出价水平变化随着拍卖的进行愈加剧烈并在拍卖末期达到最大,也表现出此类竞买者具有明显的拍卖狙击特征。endprint
第一类竞买者与第二类竞买者所不同的是他们选择在拍卖初期就积极参与竞拍,且出价次数在拍卖中后期达到顶峰。从相平面图可以看出,该类竞买者平均出价水平的一阶导数和二阶导数始终大于零且远离绝对零点,说明在整个拍卖期间出价能量持续增加,但从其出价时间可知,大多数该类竞买者在拍卖末期会选择放弃参与竞拍,且出价金额大多集中在[0-3000]低档,获胜概率并不高。
第三类竞买者获胜概率最低,出价金额多集中在[0-2000]元低档。该类竞买者出价时间较为平稳,在拍卖前中后期均参与竞拍,但在拍卖末期则较少参与竞拍。出价时间范围与其他三类相比最短,即参与竞拍时间晚而退出竞拍时间早,后期出价动力不足,所以获胜概率较低,获胜意愿不强。从相平面图来看,该类竞买者则显示出了与其他三类竞买者的明显不同,平均出价水平一阶导数为正但二阶导数始终小于零,导致其相平面图随着拍卖的进行从反方向逐渐远离绝对零点,说明出价波动在整个拍卖期间逐渐减弱。
通过对四类竞买者出价行为特征比较不难发现,从出价时间来看,四类中大部分竞买者偏好在拍卖中后期以及末期出价,其中获胜概率最低的第三类竞买者出价时间范围最短,获胜概率最高的第二类竞买者出价时间范围最长,全程参与竞拍。从平均出价金额来看,第四类竞买者出价金额最高,而第二类竞买者则拥有最低的平均出价金额。从平均出价相平面图反映的出价波动来看,仅第三类竞买者的相平面图在整个拍卖期间反方向逐渐远离绝对零点,缺乏出价动力,第四类竞买者则在拍卖末期出价波动达到最大,具有明显的拍卖狙击特征。综合来看,第二类竞买者以参与过类似拍卖且熟悉竞拍物品的经验丰富型竞买者为主,第一类竞买者则大多是缺乏竞拍经验,或由于预算约束、时间约束等而选择在拍卖末期放弃竞拍的初级竞买者,第四类竞买者则是希望以最大概率赢得拍品为目的而较少考虑出价金额问题的势在必得型竞买者,第三类竞买者则在整场拍卖中表现出出价动力不足,属于典型的围观型竞买者。五、 结论与进一步讨论
一直以来,网上拍卖中出价行为分析多从拍品角度出发,单一竞买者出价数据时间的不规则性和稀疏性为从个人角度研究竞买者出价行为特征带来困难。本文利用基于函数性稀疏数据的聚类方法,构建了条件期望距离的相异性矩阵反映竞买者出价轨迹间差异,并运用多维尺度分析、Kmeans聚类、相平面图分析方法,结合整个拍卖期间竞买者出价金额、出价时间变化以及获胜概率综合分析不同竞买者出价行为特征。研究结果表明:通过竞买者的出价轨迹聚类可将竞买者分为显著的四类,分别是经验丰富型竞买者、缺乏经验型初级竞买者、势在必得型竞买者以及围观型竞买者。其中,经验丰富型竞买者获胜概率最高,势在必得型竞买者获胜概率次之,但平均获胜出价金额最高,围观型竞买者由于获胜意愿不强烈且参与竞拍时间较短而获胜概率最低,缺乏经验型竞买者放弃参与竞拍太早而导致获胜概率较低。
Bapna[5]按进入拍卖时间、退出拍卖时间以及出价金额将竞买者划分为早出价者(Early Evaluators)、中期出价者(Middle Evaluators)、机会主义者(opportunists)、全程参与出价者(Participators)以及浅尝辄止者(SipandDippers)五类。其中,全程参与者以及机会主义者出价特征与本文中的围观型竞买者以及势在必得型竞买者相似。与Bapna不同的是,本文结合出价金额以及出价时间在整个拍卖期间的变化情况对竞买者出价行为特征进行分类,识别出经验丰富型竞买者以及初级竞买者,但未能识别出同样拥有较高获胜概率的浅尝辄止者,如何更加精确地对竞买者出价特征进行划分是本文未来的研究方向。此外,由于网上拍卖用户匿名的特性, 多数拍卖网站为保护用户隐私并不会选择将用户的真实身份公布, 为合谋出价创造了有利条件, 合谋欺诈出价(shill bidding)涌现且得不到有效抑制。一方面, 卖家通过注册虚假账号参与拍卖, 操纵出价使得最终成交价格远远高于合理价位, 侵蚀消费者剩余, 造成拍卖效率低下;另一方面, 第三方网络拍卖平台的主要收入来源仍是按照卖家拍品的最终成交价格向卖家收取一定比例佣金, 所以网站管理者并无决心清除虚假出价的动力。如何制定更加有效的拍卖制度, 规范、保障拍卖各方参与者的行为和权益成为急需考虑的问题。在合谋欺诈出价下, 竞买者的最优出价策略将发生怎样的变化, 如何运用函数性聚类方法识别竞买者中的合谋出价者并分析合谋出价对竞买者消费者剩余影响等问题也同样值得思考。参考文献:
[1]Vickrey W. Counter speculation, auctions, and competitive sealed tenders [J]. The Journal of Finance, 1961, 16(1): 837.
[2]Marshall R C, Meurer M J, Richard J F, et al. Numerical analysis of asymmetric first price auctions [J]. Games and Economic Behavior, 1994, 7(2): 193220.
[3]Maskin E, Riley J. Asymmetric auctions [J]. The Review of Economic Studies, 2000, 67(3): 413438.
[4]Hayne S, Smith C, Vijayasarathy L. Predicting sniping in eBay auctions [C]. INFORMS Conference, 2002.
[5]Bapna R, Goes P, Gupta A, et al. User heterogeneity and its impact on electronic auction market design: An empirical exploration [J]. Mis Quarterly, 2004, 28(1): 2143.
[6]Ramsay J O, Silverman B W. Applied functional data analysis: methods and case studies [M]. New York: Springer, 2002.
[7]Shmueli G, Jank W. Visualizing online auctions [J]. Journal of Computational and Graphical Statistics, 2005, 14(2): 299319.
[8]Shmueli G, Russo R P, Jank W. The BARISTA: a model for bid arrivals in online auctions [J]. The Annals of Applied Statistics, 2007, 1(2): 412441.
[9]Jank W, Shmueli G. Studying heterogeneity of price evolution in eBay auctions via functional clustering [M]∥Bernus P, Baz·ewicz J, Schmidt G J, Shaw M J. Handbook of Information Systems Series: Business Computing, New York: Springer International Publishing, 2009: 237261.
[10]嚴明义, 程诗有. 网上拍卖品的价格层级与类别对买方出价行为的影响——基于函数性数据聚类方法的分析 [J]. 当代经济科学, 2015, 37(1): 110115.
[11]Mardia K V, Kent J T, Bibby J M. Multivariate analysis [M]. San Diego: Academic Press Inc., 1980.
[12]陈封能, 斯坦巴赫, 库玛尔. 数据挖掘导论 [M]. 范明, 等译. 北京: 人民邮电出版社, 2011.
责任编辑、 校对: 李再扬endprint

