基于Barker码的一发两收超声TOFD技术在检测倾斜裂纹中的应用
,,, ,
(河海大学 物流网工程学院,常州 213022)
基于Barker码的一发两收超声TOFD技术在检测倾斜裂纹中的应用
王鹏,韩庆邦,姜学平,郑豪,许洲琛
(河海大学 物流网工程学院,常州 213022)
在传统超声TOFD技术的基础上,将Barker码激励与一发两收TOFD技术结合起来,根据两个接收探头接收声波的声程差,准确定位裂纹的两个端点,进而定量地检测倾斜裂纹。有限元仿真结果表明,基于Barker码匹配压缩后的衍射回波信号的精度可达到0.01 μs,检测倾斜裂纹角度的平均误差为1.62°。
无损检测;超声衍射时差法;倾斜裂纹;巴克码激励
传统的超声衍射时差技术TOFD[1-2](Time of Flight Diffraction) 能精确地定量检测焊缝中的垂直裂纹,但检测倾斜裂纹时会带来误差[3],难以有效检测斜裂纹。
HOSEINI[4]基于超声B扫提出一种改进型RATT(Relative Arrival Time Technique),其能够定量检测倾斜裂纹的长度与角度,但该技术仅限于检测工件底部开口斜裂纹,难以定量检测闭口斜裂纹。陈婷婷[5]提出TOFD_LWE(Locating with Ellipses of TOFD)技术,即双椭圆超声TOFD定位技术,可以检测工件内部斜裂纹的角度,但并未给出解析解,也没有进一步地验证该方法的可行性及效率。康达[6]利用两次B扫间隔、编码器移动的距离差及倾斜裂纹之间的几何关系,定量检测裂纹倾斜角度与长度,但该方法需借助超声B扫。
针对焊缝内部倾斜裂纹定量检测的问题,笔者提出一种一发两收超声TOFD技术。该技术通过处理两个接收阵元的声程声时差,可准确获知倾斜裂纹上、下端点的坐标,进而确定其长度及角度;但在计算裂纹端点坐标中,需对声速进行平方(详见1.1中的推导)。故,其对时间精度的要求很高,很小的时间误差就可能引起较大的检测误差,难以进行有效的检测。为解决时间精度问题,笔者在一发两收超声TOFD中引入Barker码激励[7]。Barker激励最先应用于雷达系统[8],由于其能显著提高检测距离与检测精度,而逐渐应用于超声无损检测[9]与超声诊断中[7]。丛森等[10]将脉冲压缩技术应用于超声TOFD检测中,对具有槽类裂纹的钢板进行了检测,并与常规的超声TOFD检测结果进行了对比,在较低的激励电压与系统增益下,实现了较高的检测信噪比及分辨率。
笔者将Barker码激励与一发两收TOFD技术结合起来,无需超声B扫查,就可以有效地定量检测焊缝中的倾斜裂纹,减小裂纹不在两探头中线上带来的误差。仿真结果表明,该方法能显著提高时间精度(达到0.01 μs),检测倾斜裂纹深度的平均误差为0.10 mm,长度的平均误差为0.24 mm,角度的平均误差为1.62°。
1 检测理论基础
1.1 一发两收超声TOFD技术的原理
一发两收超声TOFD技术的检测原理示意如图1所示。工件表面的发射阵元与两个接收阵元放置在裂纹两端(非对称);工件内部有一个闭口倾斜裂纹,斜裂纹的长度为γ,深度为d,与竖直线的夹角为θ。以工件表面水平向右为x轴正方向,竖直向上为y轴正方向,建立直角坐标系,E(xE, 0)为发射阵元坐标,R1(x1, 0),R2(x2, 0)分别为1,2接收阵元坐标,F(xF,yF)为裂纹端点坐标。

图1 一发两收超声TOFD检测原理示意
根据图1的一发两收模式,由声时、声速及声程之间的关系可得两个独立的等式。
式中:t1,t2为R1,R2接收衍射回波的声时;c为工件纵波声速。
基于公式(1),(2)可得含裂纹端点x向坐标的一元二次方程。
式中:
从式(3)中解出xF,即可计算出裂纹端点的坐标:
(5)
式中:
式(5)中xF表达式的“±”应根据实际情况选取,文中取“+”。重复上述步骤,即可得到裂纹上、下端点的坐标。设裂纹的上下端点坐标分别为Xu(xu,yu),Xb(xb,yb),裂纹的深度d,角度θ以及长度γ如式(7)表示。
1.2 Barker码激励原理
Barker码是最为常见的单次发射二进制编码[7,9],目前发现的Barker码的最长长度是13位,尚未找到更长的Barker码[11]。相比其他编码方式(Golay码,Chirp信号),Barker码为单次发射,操作最为简便。
设r(t)为发射阵元辐射的信号,其由N个紧连着的子脉冲组成。接收阵元接收的衍射回波为s(t)。基于相关性原理,二相关信号的相位编码脉冲压缩过程为接收信号s(t)与参考信号r(t)的卷积运算:先得到接收信号与参考信号的点积,再对该点积进行反傅里叶变换。Barker码激励的脉冲压缩过程示意如图2所示。
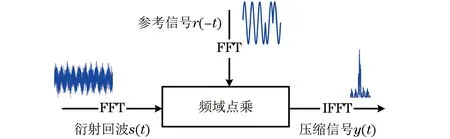
图2 Barker码激励脉冲压缩处理过程示意
2 有限元仿真
根据实际检测对象的特征,建立如图3所示的有限元仿真模型。以模型左下角为原点O,水平向右与竖直向上分别为x、y轴建立直角坐标系。模型具体参数为:长90 mm,高40 mm;填充材料为钢,纵波声速c为5 900 m·s-1;模型网格大小为1.55×10-4m,求解时间步长为1.25×10-9s,采样频率为50 MHz。模型中,狭长椭圆形裂纹中心坐标为(45 mm,15 mm),裂纹长度为6 mm,裂纹与竖直线的夹角分别为-70°,-50°,-30°,-10°,0°,10°,30°,45°,50°,70°。发射阵元激励波形为正弦调制的5位Barker码(见图4),中心频率f=5 MHz。

图3 有限元仿真模型
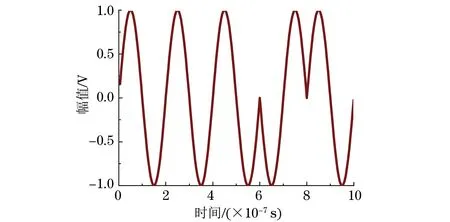
图4 正弦调制的5位Barker码
3 仿真结果与分析
文章所讨论的仅限于基于纵波的超声TOFD技术,因此只考虑工件中的纵波[12]。工件中只存在表面直通波、裂纹上端点衍射波、下端点衍射波和工件底面反射波[13],根据文献[14]中的由横波产生的变型波一般都位于底面反射波之后,其影响几乎可以忽略的结论,故文章只考虑工件中的纵波。
图5是斜裂纹与竖直线的夹角θ为45°时,模型在不同时刻的声场图,可见,图中可清晰分辨出裂纹上端点衍射波、下端点衍射波以及底面反射波。
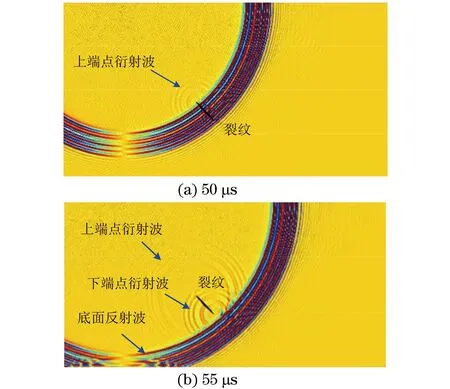
图5 裂纹与竖直线的夹角为45°时,模型在不同时刻的声场图

图6 1,2接收阵元接收的声波信号
图6是两个接收阵元接收的声波信号,图中表面直通波及底面反射波清晰可见,但是裂纹上端点衍射波与下端点衍射波的幅值极低,几乎无法分辨而难以进行有效的检测。图7是对接收阵元接收的声波进行脉冲压缩处理后得到的窄脉冲信号,其通过匹配滤波器的方式将时域较长的信号压缩成时域很窄的脉冲信号;图中表面直通波,底面反射波,裂纹上、下端点衍射波均清晰可辨,有用信号的幅值及时间分辨率显著提高,是较理想的检测波型。

图7 经脉冲压缩后的1,2接收阵元接收的声波信号
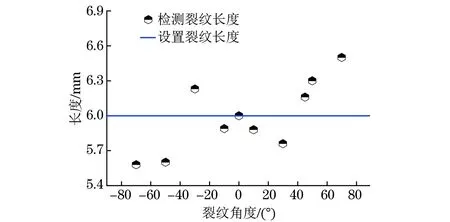
图8 检测的裂纹长度与设置长度的对比
从图7可获得裂纹上端点衍射波到达两个接收阵元的声时分别为:t1=9.74 μs,t2=10.99 μs。将模型中的参数及声时代入式(5),得到裂纹上端点的坐标(42.86 mm, 17.13 mm);同样地,裂纹下端点坐标为(47.11 mm, 12.86 mm)。通过式(7)得到裂纹的信息:裂纹深度d=17.09 mm,长度γ=6.17 mm,角度θ=46.28°。检测参数与设置的参数误差为:深度误差ed=0.03 mm,长度误差eγ=0.17 mm,角度误差eθ=1.28°。
图8是Barker码激励的一发两收TOFD检测的裂纹长度与设置长度的对比,最大误差为0.5 mm,平均误差0.24 mm;图9是检测的裂纹角度与设置角度的对比,最大误差为3.06°,平均误差为1.62°;图10是检测裂纹深度与设置深度的对比,最大误差为0.24 mm,平均误差为0.10 mm。

图9 检测的裂纹角度与设置角度的对比

图10 检测的裂纹深度与设置深度的对比
根据图7,在Barker码激励的一发两收TOFD技术中,斜裂纹上、下端点的衍射回波幅值显著提高,是较理想的检测波型。由图8~10中的数据可知,Barker码激励的一发两收TOFD能够有效地检测倾斜裂纹的长度、深度及角度。
4 结论
提出基于Barker码激励的一发两收超声TOFD技术,并用有限元仿真验证了该方法的检测能力。仿真结果表明,该方法能够较精确地检测倾斜裂纹的深度、长度和角度,检测误差能够保持在一个较小的范围内。
Barker激励结合一发两收TOFD技术的检测范围(上、下盲区),检测精度有待进一步讨论。
[1] SILK M G. The transfer of ultrasonic energy in the diffraction technique for crack sizing[J]. Ultrasonics, 1979, 17(3): 113-121.
[2] SILK M G. Changes in ultrasonic defect location and sizing[J]. NDT International, 1987, 20(1): 9-14.
[3] CIORAU P. Critical comments on detection and sizing linear defects by conventional tip-echo diffraction and mode-converted ultrasonic techniques for piping and pressure vessel welds[J]. NDT. The E-Journal of Nondestructive Testing,2006,11(5):1-7.
[4] HOSEINI M R, WANG X, ZUO M J. Modified relative arrival time technique for sizing inclined cracks[J]. Measurement, 2014, 50(50):86-92.
[5] 陈婷婷. 基于超声TOFD-LWE检测方法的缺陷识别与研究[D]. 哈尔滨:哈尔滨工程大学, 2011.
[6] 康达,张树潇,金士杰,等.基于几何方法的焊缝倾斜裂纹TOFD定量检测[J].无损检测,2016, 38(4):1-5.
[7] ZHANG H, WU S, TA D, et al. Coded excitation of ultrasonic guided waves in long bone fracture assessment[J]. Ultrasonics, 2014, 54(5): 1203-1209.
[8] DE M A, DE N S, HUANG Y, et al. Code design to optimize radar detection performance under accuracy and similarity constraints[J]. IEEE Transactions on Signal Processing, 2008, 56(11): 5618-5629.
[9] 周正干, 马保全, 孙志明,等. 相位编码脉冲压缩方法在空气耦合超声检测信号处理中的应用[J]. 机械工程学报, 2014, 50(2):48-54.
[10] 丛森, 刚铁, 张佳莹,等. LFM激励信号在超声TOFD检测中的应用[J]. 焊接学报, 2015, 36(2):63-66.
[11] NOWICKI A, LITNIEWSKI J, SECOMSKI W, et al. Estimation of ultrasonic attenuation in a bone using coded excitation[J]. Ultrasonics, 2003, 41(8): 615-621.
[12] 宋小春, 王亚午, 涂君,等. 基于超声衍射时差法的缺陷检测技术仿真分析[J]. 传感器与微系统, 2015, 34(5):55-58.
[13] BABY S, BALASUBRAMANIAN T, PARDIKAR R J, et al. Time-of-flight diffraction (TOFD) technique for accurate sizing of surfae-breaking cracks[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2003, 45(6): 426-430.
[14] BASKARAN G, BALASUBRAMANIAM K, RRA C L. Shear-wave time of flight diffraction (S-TOFD) technique[J]. NDT & E International, 2006, 39(6): 458-467.
ApplicationofUltrasoincTOFDTechnologywithOneTransmitterandTwoReceiversBasedonBarkerCodeinDetectingInclinedCracks
WANG Peng, HAN Qingbang, JIANG Xueping, ZHENG Hao, XU Zhouchen
(College of Internet of Things Engineering, Hohai University, Changzhou 213022, China)
This paper combined the Barker code excitation with the modified TOFD with double receivers on the basis of traditional TOFD technique. Based on the travelling times
by the two receivers, the positions of two crack tips were acquired to quantitatively evaluate inclined cracks. FEM simulation results showed that the time resolution of the signal compressed by Barker code excitation could be up to 0.01 μs and the average error of the estimated orientation was 1.62°.
NDT; TOFD; inclined crack; barker code excitation
TG115.28
A
1000-6656(2017)12-0040-04
2017-05-15
国家自然科学基金资助项目(11574072,11274091);江苏省重点研发计划项目(BE2016056)
王鹏(1993-),男,硕士,研究方向为通信与信息系统
韩庆邦,hqb0092@163.com
10.11973/wsjc201712009

