基于多元统计的线阵CT图像环形伪影去除方法
,,,,
(1.中国兵器科学研究院宁波分院,宁波 315103;2.浙江工业大学 机械工程学院,杭州 310014)
基于多元统计的线阵CT图像环形伪影去除方法
齐子诚1,2,倪培君1,李红伟1,唐盛明1,郭智敏1
(1.中国兵器科学研究院宁波分院,宁波 315103;2.浙江工业大学 机械工程学院,杭州 310014)
针对线阵工业CT重建图像中环形伪影干扰问题,设计一种基于多元统计的新型校正方法。首先采用灰度直方图统计结合最大类间方差法对CT图像中不同材料密度进行分类,根据材料密度分布对原始CT图像进行材料去除,然后进行极坐标系转换,对转换后的极坐标图像进行横坐标像素值统计,提取不同半径r下伪影灰度幅值统计值,最后采用原始CT图像消减伪影统计值的方式进行伪影校正。采用6 MeV线阵探测器高能工业CT系统,对含有环形伪影的不同结构CT图像进行校正试验。试验结果表明:该方法在有效去除CT图像环形伪影的同时,还能较好地保持图像细节和分辨率,显著提高了处理速度。
工业CT;环形伪影;噪声去除;多元统计
工业计算机层析技术能够不受被检测物体材料、形状、表面状况等的限制[1],给出被检测物体内部结构、组成、材料及缺损状况的二维、三维图像,是现代工业产品无损缺陷检测的一项重要手段[2]。现阶段应用较为广泛的是第三代扫描方法,其采用单射线源,具有大扇角、宽扇束、全包容被检断面的特点,且可控性强、效率高。环形伪影作为三代扫描模式中较为常见的一种伪影,不仅会影响图像的质量,还会对后续的处理、缺陷识别和尺寸测量造成干扰。因此,研究CT图像环形伪影校正方法是十分必要的。
目前,少数CT系统选用高性能探测器抑制环形伪影,但图像处理仍是主要的去环形伪影的技术手段[3]。基于图像处理技术消除CT环形伪影的方法主要分为投影正弦图校正法和极坐标校正法两类[4-10]。投影正弦图校正法在投影域直接对投影图像进行滤波,然后对恢复后的投影数据采用滤波反投影(FBP)算法进行重建,实现CT图像环形伪影的校正。极坐标校正法需要将笛卡尔坐标下的环形伪影变换为极坐标下的直线伪影,然后进行水平方向平滑滤波,最后再变换到直角坐标系中。上述校正方法对环形伪影都有不错的抑制效果,但也存在一定的不足。基于投影正弦图的校正方法虽然在质量和保真度上都要优越一些,但是存在迭代算法处理等相关参数不易确定,阈值不易选择的问题。极坐标校正法由于两次坐标变换都要用到插值,并且需要针对各个不同的图像设定不同的环形伪影滤波器的阈值,当插值和阈值设定不妥当时,容易造成图像分辨率下降、细节丢失、运算效率低下等问题。
针对上述方法的不足,笔者提出了基于多元统计的环形伪影去除方法,首先对原始图像进行直方图统计,采用多项最大类间方差分割法确定多种密度分类,并确定每一类的主元,删去图像中各个主元灰度值,再进行极坐标变换,统计伪影线分布系数,对原始图像进行映射,然后用原始数据减去伪影系数实现对异常像素的校正。通过对实际CT图像进行试验验证,结果表明该方法无需进行线条识别,在去除环形伪影的同时能保持图像的细节,有效快速地校正CT图像中的环形伪影。
1 基于多元统计的环形伪影校正
1.1 环形伪影成因
环形伪影是CT中常见的一种伪影,产生原因有X射线束硬化、重建过程中滤波器和相邻探测器响应不一致等。原始数据在经过反投影算法后,将在每个视角方向上都产生一条直线,通过持续的累加会形成包络,同时由于离散反投影需要插值运算,这往往会加大此包络的宽度,形成环形伪影,环形伪影形成原理示意与铝合金CT图像环形伪影示例如图1所示。
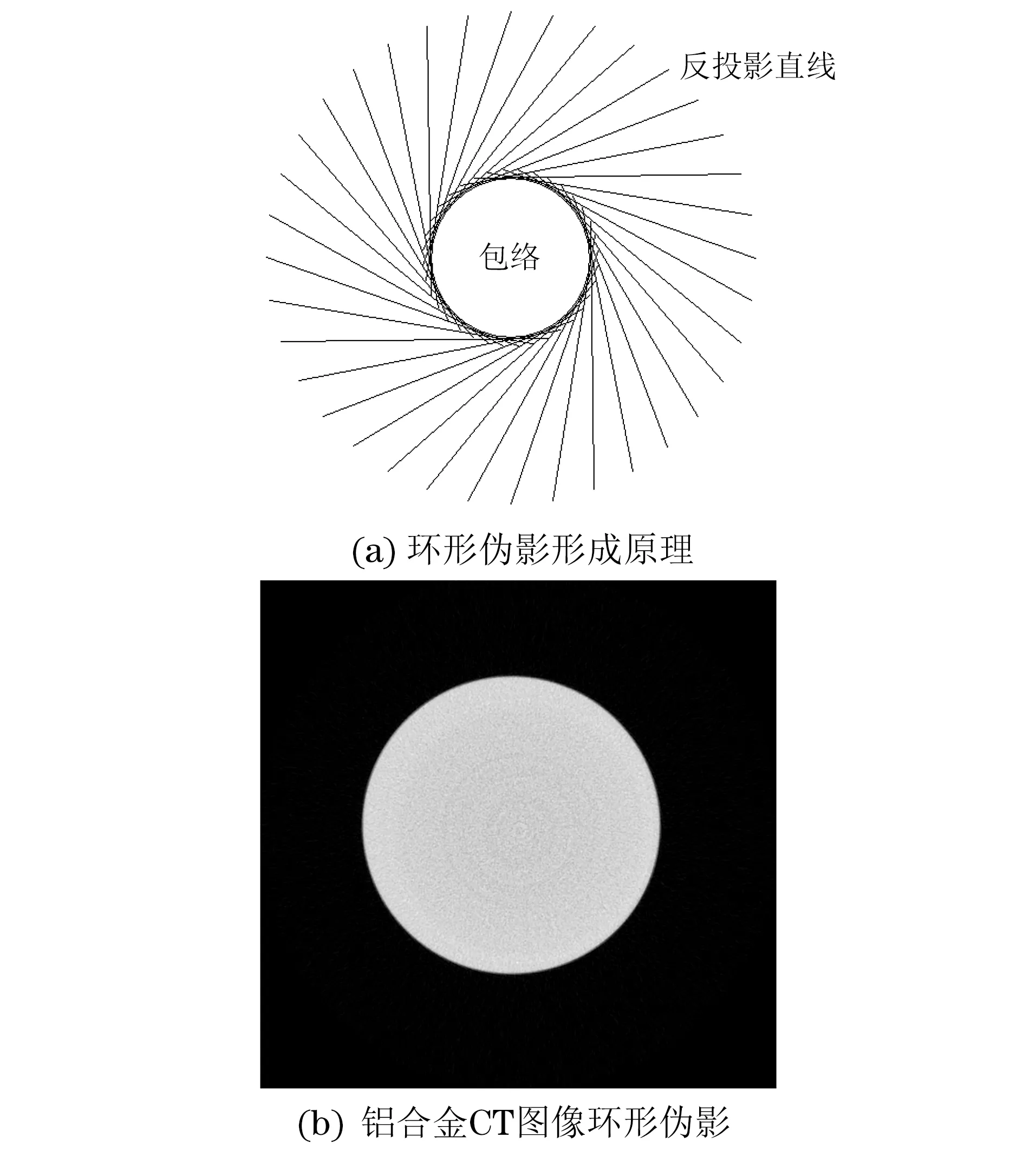
图1 环形伪影形成原理示意与铝合金CT图像环形伪影示例
在重建图像上,CT环形伪影与被检测对象往往是叠加的,表现为一系列的同心圆,并沿径向半径不断扩大。环形伪影的存在很大程度上降低了图像的质量,给基于图像的测量、识别、噪声处理以及图像分割等进一步的处理和分析带来很大的困扰。
1.2 多元直方图分类统计
多阈值最大类间方法的基本思想是在两个波峰之间找到一个统计意义上的最佳波谷,用波谷划分开两个独立的波峰,从而区分开目标与背景。设包含环形伪影的CT图像大小为N×N,该图像上任意一点的像素值可以表示为I(x,y),其中x,y分别为该点的横坐标和纵坐标,0≤x,y≤N。图像中包含M个灰度级(0,1…,M-1),灰度值为i的象素点数为Ni,由式(1)计算出图像总像素点数W。
由式(2)计算灰度值为i的图像点数占比。
设CT图像中由n种不同密度材料组成,通过不同灰度分布可把直方图大致分割成L0,L1,…,Ln个类。当邻近的两组数据的类间方差最大时,得到最佳分割阈值ti。分割后各类的均值、方差分别为ui,σi。由式(3)计算类间方差σi。

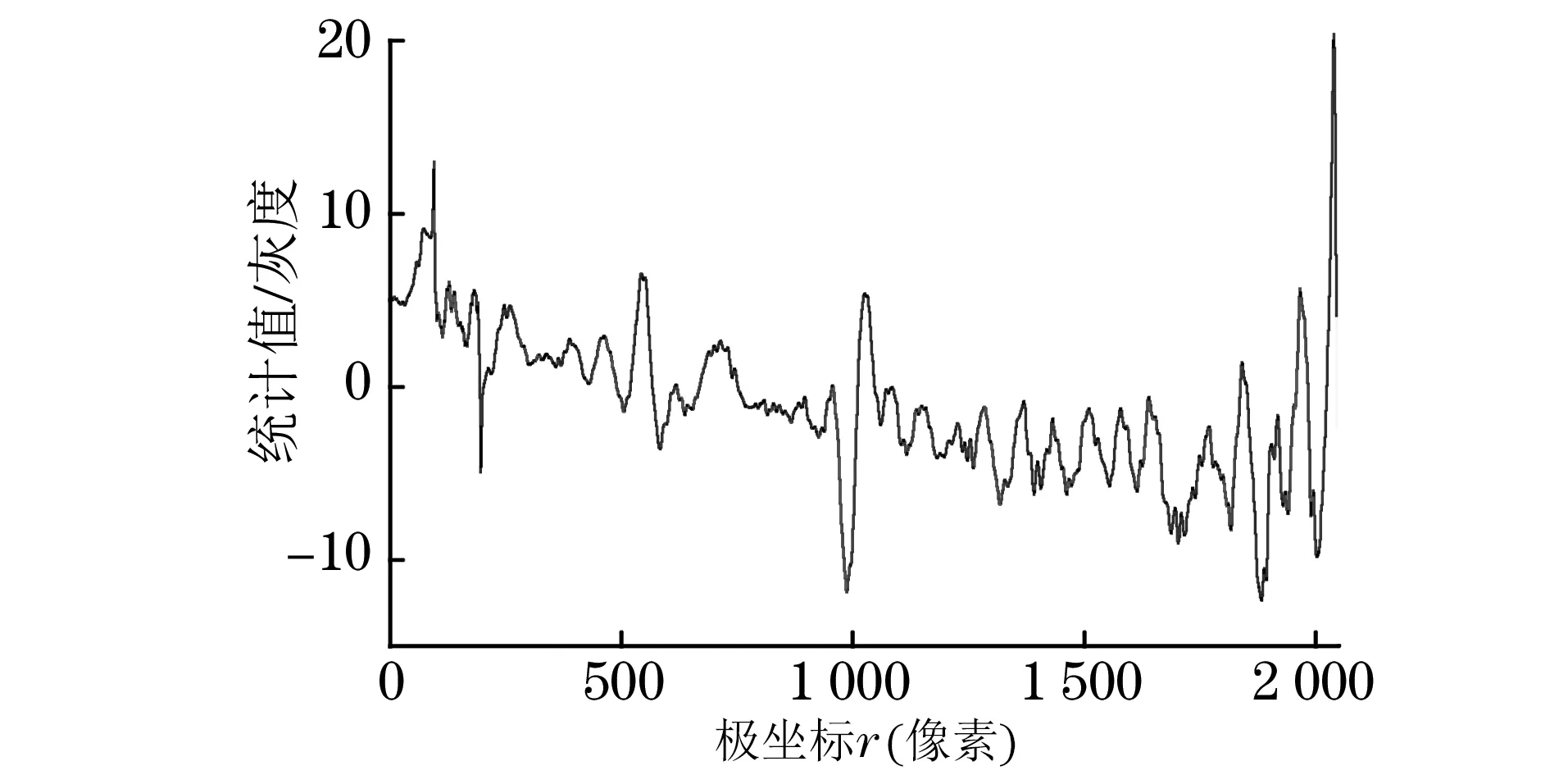
根据最大类间方差计算n个类之间的最佳分割阈值,重新分割各类,设新类为A(i),0 根据坐标系I(x,y)中,每个像素所在类进行分类,减去该点所在类的灰度均值,记为I′(x,y)。设直角坐标I(x,y)中任意一点为k,其可表示为I(xk,yk),首先判断k点的灰度属于哪个类,设k∈(tm-1,tm)即属于类A(m),该类的均值为Tm,则I′(xk,yk)=I(xk,yk)-Tm替换原来k在极坐标系θ-r所在位置的灰度值。对于灰度域中两端点数据的处理方法为,当m=1时,即类A(1)灰度范围(0,t1),则I′=I(xk,yk)-max[WM,M∈(0,t1)]。将直角坐标系中的所有点进行上述处理得到I′(x,y)。 设极坐标图像为I(r,θ),θ∈(0,2π),r∈(0,N/2)。θ取值间隔为360/(π×N)。从CT图像(直角坐标系)映射到θ-r图像(极坐标系),由式(5)计算。 式中:r为正整数,范围0≤r≤N/2,计算过程中四舍五入至最近正整数;θ数值最小间隔为360/(π×N),计算过程中四舍五入至最近间隔位。 当CT图像(直角坐标)中所有的I(x,y)运算完成以后,在θ-r图像(极坐标)中会出现以下三种情况: (1)θ-r图像(极坐标)中某一坐标点(r1,θ1)被赋值1次,则当前值即为该位置的值。 (2)θ-r图像(极坐标)中某一坐标点(r1,θ1)被赋值多次,采用多次累加得到的和除以赋值次数,求得平均值即为该坐标点的值。上述方法采用的角度θ间隔为360/(π×N),最大程度上减少了由于叠加平均而引起的图像细节的丢失。 图2 插值优先示意 (3)θ-r图像(极坐标)中某一坐标点(r1,θ1)未被赋值,则当前值需要通过在θ-r图像(极坐标)上进行,插值优先级从大到小为(r2,θ2)>(r3,θ3)>…>(r8,θ8)>(r9,θ9)。如图2所示,通过上述步骤实现从CT图像(直角坐标)映射到θ-r图像(极坐标)的转换。 设去除环形伪影后的灰度值为G(x,y),图像中心位置为(N/2,N/2),由式(6)计算该点(x,y)与图像中心的距离Lx,y。 由式(7)计算G(x,y)各个点的灰度值。 式中:Sh为滤波参数Sr,其中h=N/2-Lx,y。 对所有I(x,y)全部点进行校正处理,获得G(x,y)。 如图3所示,试验设备为北京固鸿生产的6 MeV高能工业CT系统,其空间分辨率为2 lp·mm-1,重建图像像素尺寸为4 096×4 096,重建视场半径为100 mm。采用厚度为1 mm的切片进行对比试验,微动次数均10次。采用三代扫描方式。 图3 6 MeV高能工业CT检测系统 试验对象为均质铝合金试块,如图4所示。由于工艺参数选择不当,工件CT图像含有明显环形伪影。选取局部图像进行放大处理,可见环形伪影和高密度夹杂。 图4 铝合金试块CT图 对含有环形伪影的CT图像进行伪影去除,如图4(a)所示的CT图像像素尺寸为4 096×4 096。图5为直方图统计后计算的各类的均值,进行主元消减,从图中可以发现含有较多的环形伪影,有多个相连的全环,环形伪影较原图更加明显。进行极坐标展开后的图像如图6所示,图中横线为伪影的位置,可以发现极坐标图中伪影信息基本都得到了加强。统计图6中极坐标系CT图像每行伪影的灰度均值,建立不同中心距与伪影灰度幅值的对应关系,如图7所示。根据图4(a)原图中每个像素点的位置,对应伪影灰度幅值,进行减法校正形成最终伪影去除后的CT图像,如图8所示。 图5 铝合金试块的主元消减后CT图 图6 铝合金试块的极坐标展开图像 图7 铝合金试块的伪影灰度分布图 图8 处理后的铝合金试块CT图 结合复杂结构产品对文中的伪影去除效果进行定量分析,采用高碳高铬钢零部件作为检测对象,如图9(a)所示。使用文中的多元统计方法、正弦投影方法[11]、极坐标变换方法[12]对图9(b)进行环形伪影校正。并且,采用信噪比作为图像质量评价指标,分别选取工件内部、背景和中间部位三个局部区域(局部1~局部3)进行效果比较。采用图像的信噪比作为图像质量的定量评价指标,如式(8)所示。 计算背景区域中的信噪比,得到不同校正方法灰度图像的信噪比如表1所示。 从图10和表1可看出,多元统计方法、正弦投影方法和极坐标变换方法对CT图像环形伪影的校正都有一定的抑制效果。但是,正弦投影方法的边缘细节保护效果好,图像信噪比低;极坐标变换方法图像视觉上模糊且分辨率低。综合考虑,多元统计方法可减小均匀区域标准差,提高信噪比,具有较好的图像细节保持能力,且只需进行一次坐标系变化,极大地缩短了处理时间。 图9 零件实物及其CT图 图10 零件局部区域(局部1~局部3)的试验对比效果图 灰度图像局部1图像信噪比局部2图像信噪比局部3图像信噪比原局部图24.6628.0524.53多元统计方法24.9131.8824.84正弦投影方法24.7130.4524.75极坐标变换法24.8230.1624.63 提出了一种基于多元统计的线阵CT图像环形伪影去除方法,根据CT图像直方图上多类密度区域分布的特点,采用多阈值类间方差法对CT图像灰度区域进行分割,以各个区域内主元作为该区域像素的均值进行减除,将减除后的CT图像作为伪影统计的输入图像。理论分析和试验测试结果均验证了该方法对工业CT图像环形伪影去除的有效性。相比较于正弦投影方法,该方法能减小均匀区域的标准差,提高信噪比,具有较好的图像细节的保持能力;较传统极坐标变换法,其只需进行一次坐标系变化而极大地缩短了处理时间;在保证较高的尺寸测量精度的同时,较大地提高了处理效率。 [1] 张朝宗,郭志平,张朋,等. 工业CT技术和原理[M].北京:科学出版社,2009:32-80. [2] 张俊哲.无损检测技术及其应用[M].北京:科学出版社,2010. [3] GONZALEZ R C, WOODS R E. 数字图像处理[M].北京:电子工业出版社, 2008. [4] 马继明,宋岩,王群书,等.X射线CT环形伪影去除方法[J].强激光与粒子束,2014,26(12):177-182. [5] 王珏,黄苏红,蔡玉芳,等.改进Canny算法的CT图像环形伪影校正[J].光学 精密工程,2011,19(11):2767-2773. [6] 周意超,谢明元,杨玲,等.CT环状伪影矫正方法的改进研究[J].四川大学学报(医学版),2016(3):420-424. [7] 郭宏,曾栋,张华,等.基于投影域小波滤波处理的CT图像环形伪影去除方法[J].南方医科大学学报,2015(9):1258-1262. [8] POLUDNIOWSKI G, EVANS P M, HANSEN V N, et al. An efficient Monte Carlo-based algorithm for scatter correction in keV cone-beam CT[J]. Physics in Medicine and Biology,2009,54:3847-3864. [10] 张华,黄魁东,史仪凯,等. 一种基于空气扫描的锥束CT环形伪影校正方法[J].CT理论与应用研究,2012,21(2):247-254. [11] 李保磊,杨民,傅健,等.两种CT成像环状伪影校正方法[J].光学学报,2009,29(7):1849-1853. [12] 杨俊,甄鑫,卢文婷,等.基于圆扫描轨迹的锥形束CT重建与环形伪影消除[J].南方医科大学学报,2009,29(12):2379-2382. IndustrialCTImagesRingArtifactsRemovalMethodBasedonMultivariateStatistics QI Zicheng1,2, NI Peijun1, LI Hongwei1, TANG Shengming1, GUO Zhimin1 (1.The Ningbo Branch of Ordnance Science Institute of China, Ningbo 315103, China;2.College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China) A multivariate statistical method was proposed to correct ring artifacts in industrial CT images. First, the grayscale histogram statistics and maximum interclass variance were used to classify the density in CT images. Then, the coordinate system was converted to the polar one and the abscissa pixel values were counted in the polar coordinate image and the artifacts of the gray scale amplitude were extracted at different radii. Finally, the correction was performed by subtracting artifacts from the original CT image. The CT images of different structures with ring artifacts were calibrated by using 6 MeV linear array detector high energy industrial CT system. The experimental results show that this method can effectively remove CT images from ring artifacts. The image details and resolution were well kept and the processing speed was significantly improved. industrial CT; ring artifact; noise removal; multivariate statistics TG115.28 A 1000-6656(2017)12-0020-05 2017-07-09 国家自然科学基金资助项目(61471411);浙江省自然科学基金资助项目(LQ15E010003);宁波国际科技合作资助项目(2015D10005);宁波市自然科学基金资助项目(2016A610247) 齐子诚(1984-),男,副研究员,主要从事无损检测自动化技术、图像处理等方面的研究 齐子诚, nathan1984@qq.com 10.11973/wsjc201712005
1.3 主元消减法
1.4 CT图像坐标变换
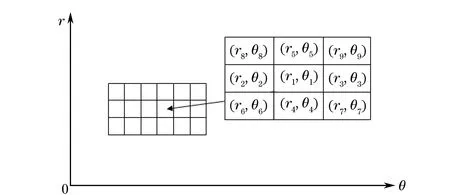
1.5 伪影均值统计
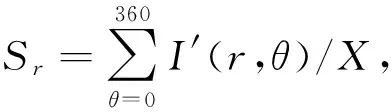
1.6 伪影校正
2 试验设备及对象
2.1 试验设备

2.2 试验对象

3 试验结果与分析







4 结语

