水流作用下一种养殖金属网衣水阻力特性的数值模拟研究

刘航飞， 陈昌平， 郑艳娜， 梁新宇

(大连海洋大学海洋与土木工程学院，辽宁 大连 116023)

水流作用下一种养殖金属网衣水阻力特性的数值模拟研究

刘航飞， 陈昌平， 郑艳娜， 梁新宇

(大连海洋大学海洋与土木工程学院，辽宁 大连 116023)

为保障深远海金属网箱养殖系统的结构安全，进行网箱结构的水动力学研究是一项重要的工作。构成金属网箱主要组成部分的金属网衣是一种小直径多孔的网状结构，在波浪和水流作用下的水动力学特性与一般的海洋工程结构物有显著不同。本文基于有限元基本原理，采用梁单元模拟金属网线结构，采用连接单元模拟网线接触部位的相互作用，并运用ABAQUS软件进行数值计算，在试验验证的基础上，分析了在水流作用下一种金属菱形链网衣在不同网目尺寸、不同网线直径情况下的水阻力变化情况。数值模拟结果表明在各种工况下，当网目尺寸由25 mm增加到35 mm、45 mm时，网衣受力增加幅度的平均值分别为14.71%和38.07%；当网线直径由2.5 mm增加到3.2 mm、4.0 mm时，各工况下网衣受力增加幅度的平均值分别为25.05%和45.06%。研究结果可以为进一步开展深海养殖金属网箱水动力特性研究提供积极的基础。

金属网衣；水阻力特性；梁单元；连接单元；数值模拟

近年来近岸网箱养殖业对海洋环境的破坏日益严重，且采用的纤维类网箱在波流作用下网衣变形严重，影响了鱼类生存空间，导致鱼类品质降低。深水金属网箱以其抗浪、抗流、耐腐蚀、轻附着、低污染等优势成为极具发展潜力的新型养殖模式。金属网衣是网箱的重要组成部分，在工作过程中，承受复杂的波浪水流作用，不仅是整个网箱系统受力的主要部分，也是整个网箱系统变形较大，容易破坏的部位，网衣的安全性已成为网箱离岸养殖过程中首要关注的问题。研究金属网衣的水阻力特性，为网衣的安全设计提供设计依据是一项重要的基础性工作。

多年来各国学者采用数值模拟和模型试验的方法对纤维类网衣的水动力特性进行了研究：采用有限差分法[1]和有限单元法[2-8]对网衣进行了数值模拟研究；采用试验方法对网衣的水阻力系数、变形和受力等水动力特性进行了研究[9-11]，采用弹簧-集中质量模型[12-16]和多孔介质模型[17]分析了网衣的水流阻力和变形。在金属网衣研究方面，Drach A等[18-19]基于有限元方法和接触算法，分析了一种金属菱形链网在静力加载作用下连接部位的应力情况。陈昌平等[20]基于CFD原理，建立了流体与金属编织网衣之间的流固耦合模型，分析了一种金属网衣在水流作用下的受力特性。尽管有许多学者对网衣水动力特性进行了较多研究，但主要针对于平面矩形或菱形网目的纤维类网衣，而对于具有三维空间结构的金属菱形链网的研究相对较少。

深远海养殖用金属菱形链网是一种小尺度多孔弹性网状结构，同时网衣在材质、网目形状、编制方式等方面与传统纤维类柔性网衣相比，具有网衣整体刚度大、网线连接方式特殊等特点，因此在波浪水流作用下的受力和变形特性与纤维类网衣有显著的不同。文中采用有限单元法，针对网线结构采用梁单元进行模拟，采用连接单元模拟网线交接处的接触，利用ABAQUS软件对一种锌铝合金菱形链网在水流作用下的水阻力特性进行了数值计算，并在试验验证的基础上分析了金属网衣水阻力大小与网目尺寸以及网线直径之间的关系，研究结果将为进一步开展整体网箱系统的水动力特性研究打下良好的数模基础。

1 数学模型

1.1 网衣模型

金属菱形链网具有较为复杂的三维空间结构。图1为网目大小m=45 mm，直径大小d=4.0 mm的锌铝合金菱形链网模型图。在网衣结构建模时，将其投影截面近似为椭圆，长轴a=3.5 cm，短轴b=1.8 cm。然后按照螺距s=6.7 cm进行拉伸，形成一个总长为0.8 m长的链条。最后将链条进行阵列，组合成一个长宽为0.8 m×0.8 m的金属网衣。在有限元软件ABAQUS中建立的模型尺寸采用毫米制。

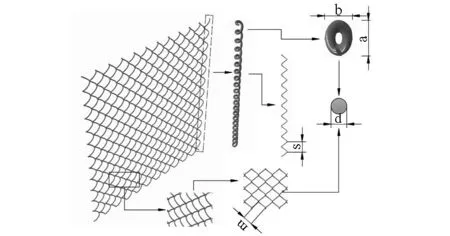
图1 金属菱形链网模型图

1.2 单元划分

金属网衣采用两节点的梁单元进行模拟，局部网格的划分见图2，针对图1所示网衣模型，划分后的节点总数为6 358个，单元总数为6 336个。在两根网线交接部位加入连接单元，模拟网线之间的接触作用，计算时约束接触处3个位移方向的相对自由度，不约束相对旋转自由度。

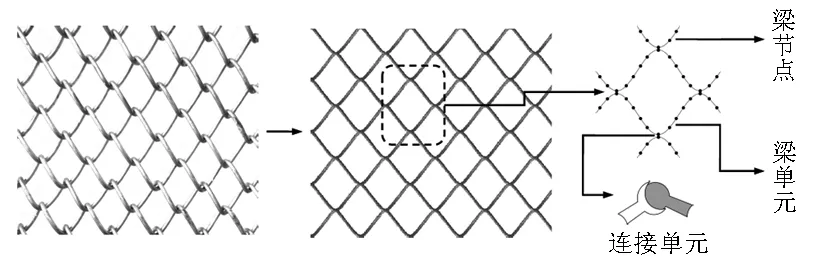
图2 网衣单元划分示意图

1.3 数值方法

1.3.1 受力分析

(1)重力与浮力。由于网衣全部浸没在水面以下，因此将重力和浮力一起考虑。圆形截面杆件的重力和浮力的计算公式[21]为：

(1)

式中：PZ为杆件所受重力和浮力的合力，N；ρf和ρw分别为金属网衣的密度和水的密度，kg/m3；D为杆件的横截面直径，m；l为杆件长度，m；V为杆件体积，m3。

(2)水流阻力。浸没在水中的网衣受到的水流阻力采用Morison公式[22]计算。为了便于计算，将水流阻力沿杆件的法向和切向分解为法向水流阻力和切向水流阻力，如图3所示。

(2)

式中：Fn为单位长度的法向阻力，N；Cn为法向阻力系数；Δvn为流体相对于杆的速度在杆法面内的分量，m/s。

(3)

式中：Ft为单位长度的切向阻力，N；Ct为切向的摩擦力系数；Δvt为流体相对于杆的速度在杆切面内的分量，m/s。

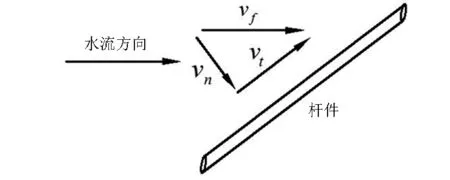
图3 流体速度沿杆的切向和法向分量

采用Morison公式计算小尺度构件在水流作用下的受力时，根据网衣的结构特点及相关文献，本文采用Choo[23]等提出的速度力系数与雷诺数的关系式来计算法向和切向水阻力系数。

(4)

(5)

式中：s=0.077 215 665+ln(8/Ren)；Ren=ρwVnD/μ；μ为水黏性系数，kg/(m·s)。

1.3.2 运动方程的构建和求解

网衣采用两节点的梁单元进行模拟。在三维空间下，每一个节点有3个位移自由度，其离散化运动方程[24]：

(6)

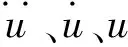
(7)

式中：Me、Ce、Ke、Qe分别为单元节点的质量矩阵(kg)、阻尼矩阵(N·s/m)、刚度矩阵(N/m)和载荷向量(N)；N为插值函数矩阵；B为应变矩阵；D为弹性矩阵；f为由单元体积力组成的节点荷载矩阵，N；T为单元表面力组成的节点荷载矩阵，N；Ve为单元体积(m3)；Se为单元面积(m2)；ρ为质量密度(kg/m3)；η为阻尼系数(N·s/m)。图4为动力隐式算法流程图。

图4 动力隐式算法流程图

网线交接处采用连接单元模拟，连接单元的两个节点分别与交接处两个梁单元节点相重合，因此连接单元节点控制方程与梁单元节点控制方程相同。离散化运动方程采用ABAQUS/Standard直接积分法中的动力隐式算法进行求解。

2 试验验证

2.1 试验概况

本试验采用原型的锌铝合金菱形链网，依据目前实际工程采用的网衣情况，结合研究内容，试验选用方形网衣，平面尺寸为80 cm×80 cm，网线直径分别为2.5 mm、3.2 mm、4.0 mm，网目尺寸分别为25 mm、35 mm、45 mm，金属网丝密度为6 300 kg/m3，弹性模量193 Gpa，泊松比为0.3。结合网线直径及网目尺寸大小，共进行了9组网衣试验。试验过程中，网衣固定在定制的铁质框架上，金属网衣四边与框架连接，框架上部为传感器和数据采集系统，网衣距离水面15 cm，如图5所示。试验采用拖拽方法，拖车速度分别为0.2 m/s、0.4 m/s、0.6 m/s、0.8 m/s、1.0 m/s。网衣受力值为框架与网衣总受力试验值减去单独框架拖拽试验受力值。

图5 网衣实验布置图

2.2 计算结果验证

根据网衣试验的边界条件及试验工况，采用ABAQUS中动力隐式算法进行网衣水阻力数值计算，并将计算结果与试验结果进行比较。图6为五种流速条件下数值计算结果与试验结果的比较。

由图可知，各种工况下数值计算结果与试验结果随流速的变化均表现出相同的变化趋势，计算值与试验值拟合程度良好。以试验值为基准，统计5种流速条件下各工况下计算值与试验值之间的相对误差见表1。表中每一种网衣相对误差表示在5种流速条件下得到的网衣受力的计算值与试验值相对误差平均值，平均相对误差表示所有工况下网衣受力的计算值与试验值相对误差平均值。由表1可知，各种工况下网衣受力计算值与试验值的相对误差最大值为10.69%，最小值为5.23%，相对误差平均值为8.13%。由图6及表1可以表明，采用本文建立的网衣水阻力计算模型，可以很好地计算金属菱形链网在水流作用下受到水阻力大小，与试验结果误差较小，可以为进一步进行网箱整体受力数值计算提供参考。

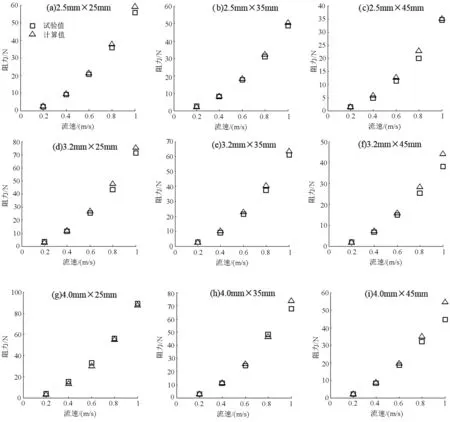
图6 网衣受力试验值与模拟值对比图

表1 水流阻力相对误差表

3 分析讨论

3.1 网衣水阻力与网目尺寸的关系

由计算结果可知，在流速与网线直径相同，网目尺寸不同条件下，金属菱形链网受到的水阻力有较明显差异。图7为在网线直径分别为2.5 mm、3.2 mm和4.0 mm情况下，对应网目尺寸分别为25 mm、35 mm、45 mm的网衣在不同流速条件下所受的水阻力比较。

由图7可知，在相同网线直径与相同流速条件下，网衣水阻力均随着网目尺寸的增加有较明显的减小，当网目为25 mm时，网衣受力最大；网目为35 mm次之；网目为45 mm时受力最小。分别以较小网目尺寸网衣受力值为基准，分析各工况下相对较大网目尺寸的网衣受力减小幅度平均值，统计情况见表2，表中35 mm/25 mm表示网目尺寸为35mm的网衣相对于网目尺寸为25 mm的网衣受力减小幅度，其他表示含义类同。

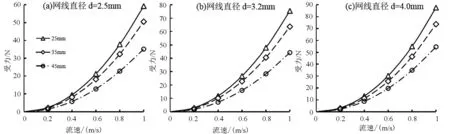
图7 网衣水阻力随网目尺寸的变化

表2 网目尺寸变化引起的网衣水阻力变化幅度统计

由表2可知，在3种网线直径条件下，各工况下3组对比网衣的受力值平均减小幅度分别为14.71%，27.39%，38.07%。不同网线直径情况下，随网目尺寸的增加，网衣受力减小幅度值差异不明显。由于在水流作用下，平面网衣受力大小与网衣在水流作用方向的投影面积成正比例关系，因此当菱形链网平面尺寸及网衣网线直径相同情况下，网目尺寸增加，网衣在水流作用方向的投影面积减小，因此网衣整体受力也随之减小。

3.2 网衣水阻力与网线直径的关系

由计算结果可知，在流速与网目尺寸相同，网线直径不同条件下，金属菱形链网受到的水阻力有较明显差异。图8为在网目分别为25 mm、35 mm、45 mm情况下，对应网线直径分别为2.5 mm、3.2 mm和4.0 mm的网衣在不同流速条件下网衣所受的水阻力比较。

由图8可知，在网目尺寸和流速相同条件下，网线直径增加，其所受的水流阻力随之有明显增加。各种工况下3种网目尺寸的网衣在直径为4.0 mm时受到的水阻力最大，直径为3.2 mm的网衣次之，网衣直径为2.5 mm时受到的水阻力最小。分别以较小网线直径的网衣受力值为基准，分析各工况下相对较大网线直径的网衣受力增加幅度平均值，统计情况见表3，表中3.2 mm/2.5 mm表示网线直径为3.2 mm的网衣相对于网线直径为2.5 mm的网衣受力增加幅度，其他表示含义类同。

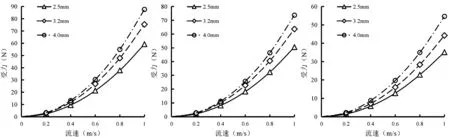
图8 网衣水阻力随网线直径的变化

表3 网线直径变化引起的受力变化幅度统计表

由表3可知，在3种网目尺寸条件下，各工况下3组对比网衣的受力增加平均幅度分别为25.05%、16.0%、45.06%。在水流作用下，平面网衣受力大小与网衣在水流作用方向的投影面积成正比例关系，因此当菱形链网平面尺寸及网目尺寸相同情况下，网线直径增加，网衣在水流作用方向的投影面积增加，因此网衣整体受力也随之增加。

4 结论

本文基于有限元基本原理，采用梁单元和连接单元建立了金属菱形链网模型，通过动力隐式求解节点运动方程。在数值模拟结果与试验结果拟合良好的基础上，分析讨论了在水流作用下金属菱形链网受力与网目尺寸及网线直径之间的关系：在水流作用下，网衣水阻力随着网目尺寸的增加而逐渐减小，当网目尺寸由25 mm增加到35 mm、45 mm时，对应的网衣受力的平均减小幅度分别为14.71%和38.07%；网衣水阻力随着网线直径的增加而逐渐增大，当网线直径由2.5 mm增加到3.2 mm、4.0 mm时，对应的网衣受力的平均增加幅度分别为25.05%和45.06%。

□

[1] BESSONNEAU J S, MARICHAL D. Study of the dynamics of submerged supple nets (applications to trawls)[J]. Ocean Engineering, 1998, 25(7):563-583.

[2] TSUKROV I, EROSHKIN O, FREDRIKSSON D, et al. Finite element modeling of net panels using a consistent net element[J]. Ocean Engineering, 2003, 30(2):251-270.

[3] DECEW J, OSIENSKI M, DRACH A, et al. Effect of the bending stiffness on the volumetric stability of fish cages with copper alloy net[C]// V International Conference on Computational Methods in Marine Engineering. 2013.

[4] LI L, FU S, XU Y, et al. Dynamic responses of floating fish cage in waves and current[J]. Ocean Engineering, 2013, 72(7):297-303.

[5] LI L, FU S, LI R. Dynamic Responses of the Floating Cage System in Current and Waves[C]// ASME 2012, International Conference on Ocean, Offshore and Arctic Engineering. 2012:239-248.

[6] LI L, FU S, XU Y. Nonlinear hydroelastic analysis of an aquaculture fish cage in irregular waves[J]. Marine Structures, 2013, 34(34):56-73.

[7] 崔勇,关长涛,万荣,等.基于有限元方法对波流场中养殖网箱的系统动力分析[J].工程力学, 2010,27(5):250-256.

[8] 崔江浩.重力式养殖网箱耐流特性的数值模拟及仿真[D].青岛:中国海洋大学, 2005.

[9] 詹杰民,胡由展,赵陶,等.渔网水动力试验研究及分析[J].海洋工程, 2002, 20(2):49-53.

[10] 李玉成,桂福坤.平面无结节网衣水阻力系数的试验研究[J].海洋学报, 2006, 28(5):145-151.

[11] 李玉成,桂福坤.平面有结节和无结节网目试验及水阻力系数的选择[J].中国海洋平台, 2005, 20(6):11-17.

[12] 黄小华,郭根喜,胡昱,等.波流作用下深水网箱受力及运动变形的数值模拟[J].中国水产科学, 2011,18(2):443-450.

[13] 陈昌平,李玉成,赵云鹏,等.波流共同作用下单体网格式锚碇网箱水动力特性研究[J].水动力学研究与进展,2009, 24(4):493-502.

[14] CHEN C P, LI Y C, ZHAO Y P, et al. Numerical Analysis on the Effects of Submerged Depth of the Grid and Direction of Incident Wave on Gravity Cage[J]. China Ocean Engineering, 2009, 23(2):233-250.

[15] CHEN C P, ZHAO Y P, LI Y C, et al. Numerical analysis of hydrodynamic behaviors of two net cages with grid mooring system under wave action[J]. China Ocean Engineering, 2012, 26(1):59-76.

[16] ZHAO Y P, WANG X X, DECEW J, et al. Comparative Study of Two Approaches to Model the Offshore Fish Cages[J]. China Ocean Engineering, 2015, 29(3):459-472.

[17] BI C W, ZHAO Y P, DONG G H, et al. A numerical analysis on the hydrodynamic characteristics of net cages using coupled fluid-structure interaction model[J]. Aquacultural Engineering, 2014, 59(2):1-12.

[18] DRACH A, TSUKROV I, DECEW J, et al. Engineering procedures for design and analysis of submersible fish cages with copper net for exposed marine environment[J]. Aquacultural Engineering, 2016, 70:1-14.

[19] DRACH A, TSUKROV I, DECEW J, et al. Design and modeling of submersible fish cages with copper net for open ocean aquaculture[C]// International Conference on Computational Methods in Marine Engineering, 2014.

[20] 陈昌平, 王文, 郑佳成,等. 水流作用下平面金属网衣水阻力特性数值模拟[J]. 大连海洋大学学报, 2017, 32(3):363-368.

[21] 苏炜,詹杰民.水流作用下渔网养殖空间变化的计算方法[J].海洋工程, 2007, 25(1):93-100.

[22] GIGNOUX H, THOMPSON L D, MESSIER R H. Computational Model of Aquaculture Fin-fish Net-pens[C]// Proceedings of an International Conference. University of Hawaii Sea Grant College Program. Maui, Hawaii, 1997:107-129.

[23] CHOO Y I, CASARELLA M J. Hydrodynamic Resistance of Towed Cables[J]. Journal of Hydronautics, 1971, 5(4):126-131.

[24] 王勖成.有限单元法[M].北京:清华大学出版社, 2003:469-522.

Studyofthenumericalsimulationofcharacteristicsofdifferentflowresistancesonametalchain-linknetforaquacultureundercurrents

LIUHangfei,CHENChangping,ZHENGYanna,LIANGXinyu

(SchoolofOceanandCivilEngineering,DalianOceanUniversity,Dalian,Liaoning116023,China)

It is an important work to study the hydrodynamic characteristics of the net structure to guarantee the safety of the whole net cage system in deep open sea. The most widely used copper alloy net in aquaculture cages is of the “chain-link” type mental net, which is a kind of porous structure with a small diameter, whose hydrodynamic characteristics under the waves and currents is significantly different from general ocean engineering structures. Based on the finite element method, the chain-link nets and the interaction between them are simulated by the beam element and connector element in the ABAQUS software. After verification by the experiment data, the different flow resistances on the net under currents with different net diameters and mesh sizes were analyzed. The numerical simulation results showed that as the mesh size increases from 25mm, 35mm to 45mm, the average value of the flow resistance increases with the amplification of 14.71% and 38.07% respectively under various operating modes. Similarly, the average value of flow resistance increases with the amplification of 25.05% and 45.06% respectively under various operating modes as the net diameter increases from 2.5 mm, 3.2 mm to 4.0 mm. The research provides a positive foundation for further study of the hydrodynamic characteristics of deep-sea aquaculture metal cages.

metal net; flow resistance characteristics; beam element; connector element; numerical simulation

10.3969/j.issn.1007-9580.2017.09.013

2017-11-01

国家自然科学基金资助项目(31572663)

刘航飞(1995—)，男，硕士研究生，研究方向：水工结构工程。E-mail：18340831879@163.com

郑艳娜(1978—)，女，副教授，博士，研究方向：港口、海岸及近海工程。E-mail：zhengyn@dlou.edu.cn

TV131.6

A

1007-9580(2017)06-073-07