城市地貌高空台风特性及湍流积分尺度的研究

王澈泉,李正农,胡佳星,张学文,周利芬,曹守坤

(湖南大学 建筑安全与节能教育部重点试验室,湖南 长沙 410082)

城市地貌高空台风特性及湍流积分尺度的研究

王澈泉,李正农*,胡佳星,张学文,周利芬,曹守坤

(湖南大学 建筑安全与节能教育部重点试验室,湖南 长沙 410082)

基于2014年第10号台风“麦德姆”在城市地貌的高空实测风场资料，共选取五个时距(30 s、1 min、5 min、10 min和20 min)进行分析，得到平均风速、风向、湍流度、阵风因子和脉动风速谱等强风特性；然后采用两种基于Taylor假定的方法来计算湍流积分尺度，分别从平均风速、湍流度和阵风因子等要素来探讨不同时距对湍流积分尺度的影响。分析结果表明：当平均时距为5min时,计算得到的平均风速较大、湍流度和阵风因子均较小，对应的方差与变异系数也较小，根据其计算得到的湍流积分尺度分布最为集中，其中又以自相关函数积分法得到的方差最小，最为合理。

湍流特性；自相关函数；指数衰减率；积分尺度

0 引 言

大气边界层是人类活动的主要场所，建筑物受到大气边界层内空气流动的影响，其湍流特性研究是结构风工程的主要内容之一。2000年庞加斌等人[1]在上海浦东城市近郊地区20 m高度处采集了两次强风样本数据，分析得到近地面的湍流积分尺度处在80 m左右；李家亮[2]等在广东某海岛60 m高塔上采集了采集了“黑格比”台风风场数据，分别用自相关函数积分法和Karman谱拟合法对湍流积分尺度进行对比分析研究；王旭[3]等人基于上海浦东沿海采集到的“梅花”台风在10 m、20 m和40 高度处的风场实测数据，分析湍流积分尺度随平均风速、观测高度及平均时距的变化规律；胡尚瑜[4]等人基于广东沿海10 m高度处“灿都”台风的现场实测数据，分析来流方向不同和不同台风区域的湍流积分尺度。我国目前对湍流积分尺度的研究主要集中在沿海近地，对城市高空台风风场研究甚少，因此有必要进行研究。

湍流积分尺度与风场数据长度和平稳程度有关[5]。Flay[6]等通过8个并列的10 m高塔和3个20 m高塔采集台风风场数据，总结了积分尺度的分析方法；庞加斌[7]等通过风洞模拟湍流的单点及多点测量分析，证明Taylor假设的合理性，采用自相关函数法简单可靠；刘欢[8]基于三组珠江口崖门的实测资料，得到基于Taylor假设的自相关函数积分法所得计算结果最为稳定可靠，自相关函数能较好地满足指数衰减率。

本文基于城市高空“麦德姆”台风过程中长时间序列的实测数据，共选取五个时距(30 s、1 min、5 min、10 min和20 min)进行分析，得到平均风速、风向、湍流度、阵风因子和脉动风速谱等湍流特性。然后采用两种基于Taylor假定的方法来计算湍流积分尺度，分别从平均风速、湍流度和阵风因子等要素，来探讨不同时距对城市高空台风的湍流积分尺度的影响，确定出比较合理、稳定的尺度分析时距。

1 实测概况

实测风速仪设置在温州市华盟商务广场顶部，该楼东南面是一片开阔地，西北面存在少量的高层，属于城市市郊地貌，试验楼周围环境见图1。在华盟商务广场顶部东南角设置一台YONG型机械式风速仪，将其固定在楼顶9m高的直杆上，风速仪离地高度约为175 m。风速仪正北安装，风向角定义北风为φ=0°，按俯视顺时针增大，即东风为φ=90°，其他角度顺时针依此类推。采用优泰数据采集仪进行数据采集，采样频率为25.6 Hz。

“麦德姆”台风于2014年7月23日15时在福建沿海登陆，进入内陆之后再进入温州市区，图2为“麦德姆”台风的移动路径。台风登陆进入市区之后，由于受到城市下垫面的影响，实测得到的湍流度较大，且顺风向湍流度大于横风向湍流度[9]。当台风开始影响温州地区时开始采集数据，共采集了30 h的风场数据。本文选取了在10 min时距下平均风速大于10 m/s的数据段(从7月24日06时55分到13时42分长达6.7 h)进行分析。图3为分析数据段的风速、风向时程。

2 实测风场特性

2.1 平均风速和风向角

根据下列公式计算风速的两个分量(如图4所示)。

平均风速U和平均风向角θ为：

根据(1)～式(6)，图5给出了“麦德姆”台风10 min平均时距下平均风速、平均风向角时程。图6给出了台风“麦德姆”10 min平均时距下整个样本的顺风向、横风向的脉动风速。10 min时距下平均风速均值为12.99 m/s，最大值为14.65 m/s，平均风向角为124.54°。

2.2 湍流度

湍流度与脉动风速均方根、平均风速的关系为：

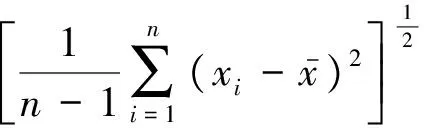
图7给出了10 min平均时距下顺风向和横风向湍流度随平均风速的变化情况，其均值分别为0.238和0.189。目前有多个经验公式用于估算顺风向湍流度，如我国荷载规范[7]给出的公式为：

式中I10为10 m高度处的名义湍流度，对应C类地貌取0.23[10]；α为风速剖面指数律的指数取α=0.22[10]；z为离地高度，取175 m。按式(8)计算的顺风向湍流度为0.123(Iu=0.23×(175/10)-0.22)，这与实测湍流度均值相差较大，主要是因为台风从福建沿海登陆之后再进去温州市区，由于城市下垫面的影响会造成风场有一定的紊乱，加上离开暖洋面后失去了维持对流所需的热源等原因，台风迅速削弱，造成其湍流度较大，同时Iu>Iv。从图7可以看出，湍流度随着平均风速的增大而减小。

(a) 顺风向

(b) 横风向

图7湍流度与平均风速的关系
Fig.7Relationshipbetweenturbulenceintensityandmeanwindspeed

2.3 阵风因子

阵风因子Gi(tg) (i=u,v)平均风速U的关系：

本文阵风持续期取tg=3 s。根据式(9)、式(10)，图8给出了台风“麦德姆”10 min平均时距下阵风因子随平均风速的变化关系。图9反映了阵风因子随湍流度变化的关系。由于试验楼距离海岸有20 km，处于城市地貌之中，台风登陆之后，城市地貌的粗燥下垫面对这种旋涡式气流的动力作用会被放大，从而产生的阵风因子有一定波动[11]。顺风向阵风因子在1.28～1.67之间波动，横风向在0.13～ 0.19间波动，其均值分别为1.445和0.157。可以看出阵风因子虽然有一定波动,但是其分布比较集中，波动范围小。它随着平均风速的增大而减小；与湍流度之间的线性关系更为清晰，随着湍流度的增大而增大。

(a) 顺风向

(b) 横风向

图8阵风因子与平均风速的关系
Fig.8Relationshipbetweengustfactorandmeanwindspeed

2.4 脉动风速功率谱

普遍认为Von Karman谱能准确地反应脉动风的统计特性。

横风向

(12)

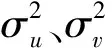
(a) 顺风向脉动风速功率谱密度

(b)横风向脉动风速功率谱密度

图10脉动风速功率谱密度
Fig.10Powerspectrumdensityoffluctuatewindvelocity

3 湍流积分尺度

湍流积分尺度与数据的长度和平稳程度有关：

3.1 Taylor假设

如果湍流旋涡以平均风速U迁移，则脉动速u(x1,t+τ)可以定义为u(x1-x,t),x=Ut，这就是Taylor假设。根据Taylor假设，式(13)可改写为

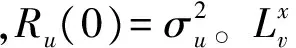
3.2 计算方法

实测过程中，根据Taylor假设，将多点测量简化为单点测量。本文采用两种方法计算，如下所示：

(2) 根据Taylor假设，自相关函数也符合指数衰减率[12]，因此将式(14)改为

3.3 不同时距下的风场特性

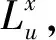
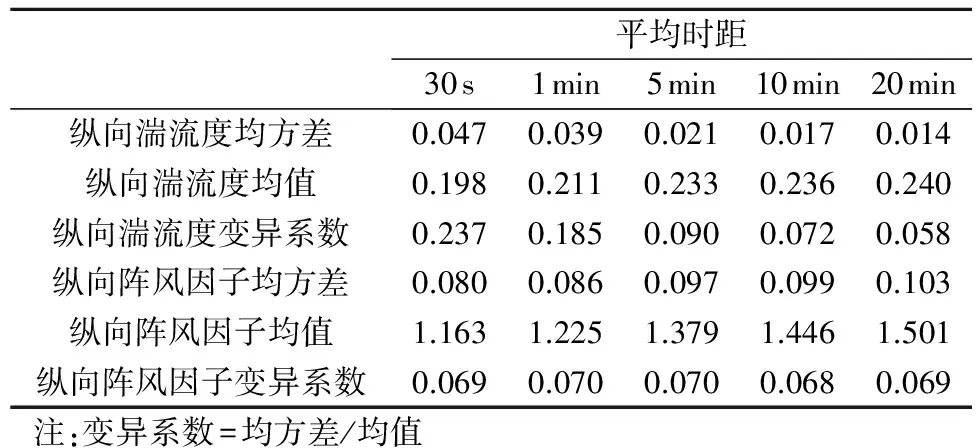
表1 顺风向湍流度、阵风因子变异系数Table 1 Coefficient of variation of turbulence intensity and gust factor

从表1和表2可以看出，时距小平均风速极值大，湍流度小但其变异系数(变异系数为均方差与均值的比值)大，表现为不稳定；时距大平均风速极值小，湍流度大但其变异系数小，最为稳定。因此可知随着时距的增大，湍流度的均值增大，但其变异系数却变小，这说明随着时距的增大，湍流度增大，却更加稳定。随着时距的增大，阵风因子均值增大，但其变异系数却基本相同，这说明随着时距增大，阵风因子的均方差与均值成线性关系。为了得到这样一时距，在其下计算得到的风速较大，湍流度和阵风因子较小，变异系数也较小。综上分析可知，当时距为5 min时最为符合，其湍流度和阵风因子分别为0.233和1.379。

表2 不同平均时距下湍流度、阵风因子统计结果Table 2 Different time intervals turbulence intensity and gust factor

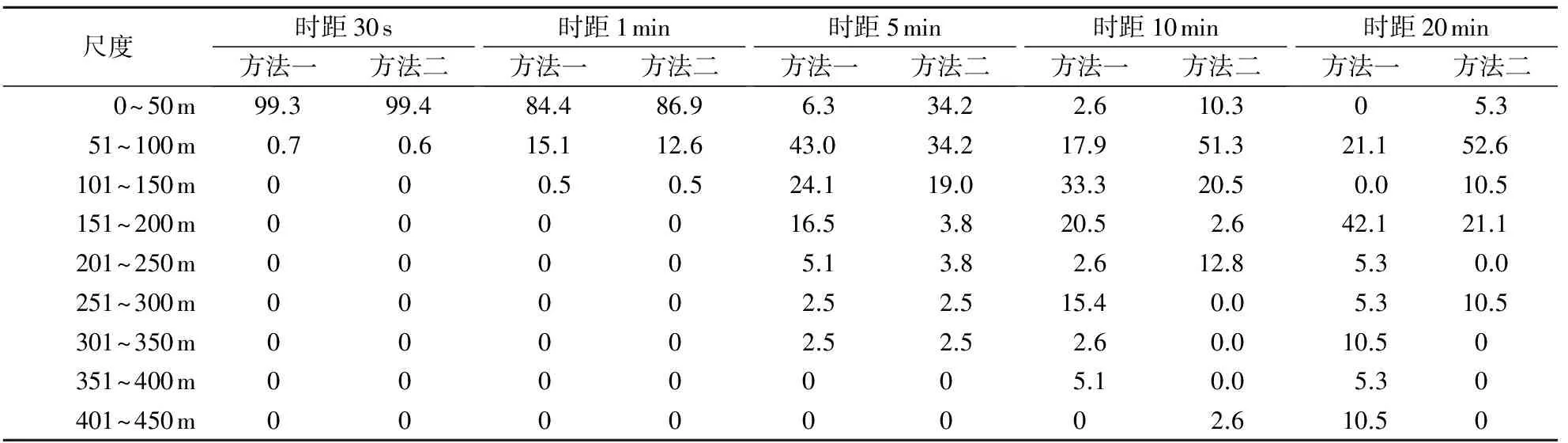
表3 湍流积分尺度概率分布表(单位：%)Table 3 Probability distribution of the vertical turbulence integral scale(unit:%)

自相关函数积分法和指数衰减拟合法均是基于Taylor假定对自相关函数进行积分。从表3可以看出，时距的选取对湍流积分尺度有很大的影响。时距为30 s时，积分尺度主要分布在50 m以内。两种方法计算的积分尺度均值分别为14.41 m和14.48m；当时距为1 min时，积分尺度均值分别为31.36 m和27.62 m；当时距为5 min时，积分尺度均值分别为120.46 m和66.36 m，较前两个时距显著增大，这三个时距下的积分尺度分布较为集中；当时距为10 min时，积分尺度均值进一步增大到166.84 m和110.12 m，但两种方法得到的积分尺度分布均较为离散；当时距为20 min时，此时距下的积分尺度更为分散，其均值达到最大，分别为215.97 m和119.38 m。可以看出，随着时距的增大，积分尺度的分布范围更广，更为分散，但其对应的积分尺度更大，也就是说明积分尺度随着时距的增大而增大。

从图11可知，在相同平均风速下，方法一得到的积分尺度随着平均时距的增大而增大。方法二中平均风速为14 m/s、12 m/s时得到的纵向湍流积分尺度随着时距的增大而增大；平均风速为13 m/s 时呈现先增大后减小的趋势、在时距5 min下得到的尺度最大。总体上看，在平均风速相同的情况下，积分尺度随着平均时距的增大而增大；在相同时距下，平均风速越大其积分尺度越大。由图11和图12可以看出，两种方法计算得到的湍流积分尺度分布形状类似，这说明，自相关函数能较好地满足指数衰减率。

从图12可以看到，利用两种方法计算得到的湍流积分尺度随着平均时距的增大而增大。两种方法得到的纵向湍流积分尺度的比例分别为0.169∶0.323∶1.000∶1.418∶1.810和0.158∶0.309∶1.000∶1.191∶1.082。当时距为30 s时，两者差别不大，但随着时距的增大，二者的湍流积分尺度之差越大。两种方法计算得到的积分尺度均方差在30 s和1 min两个时距基本相等，随着时距的增大，方法一递增，方法二先增大后减小，极值点出现在时距为10 min时，这也说明了随着时距的增大，积分尺度的分布范围更广泛。当时距为30 s时，两种方法的变异系数基本相同，说明其稳定性相差无异，但随着平均时距的增大，方法一的变异系数随着平均时距增大呈现先减小后增大的趋势，方法二的变异系数随着时距的增大呈现出先增大后减小的趋势，这也从另一个方面证实了时距对积分尺度的影响。变异系数曲线的拐点都出现在时距为5 min下，可以看出自相关函数积分法在稳定性方面明显优于指数衰减拟合法。

本文从平均风速、湍流度和阵风因子等湍流特性探讨不同时距对城市高空台风的湍流积分尺度的影响。综上所述，当平均时距为5 min时，风速大、湍流度和阵风因子小、其变异系数小，此时距下得到的强风特性最为合理；此时距计算得到的积分尺度分布最为集中，积分尺度也较大，其中自相关函数积分法得到的方差最小。因此当平均时距为5 min时，采用自相关函数积分法得到的湍流积分尺度最为合理。

4 结 论

通过对城市地貌高空台风“麦德姆”观测数据分析得到了其湍流特性，并探讨了在两种计算方法下湍流积分尺度与平均时距的关系。得到以下结论：

(1) 分析比较5种时距下台风特性。时距小，平均风速大，湍流度小，但其变异系数大，不稳定；时距大，平均风速小，湍流度大，但其变异系数小，最为稳定。综合比较，当时距为5 min时，风速较大，湍流度和阵风因子较小，其变异系数也较小，最为合理。

(2) 在相同平均风速下，积分尺度随着平均时距的增大而增大；同一时距下，平均风速越大其积分尺度越大。两种方法计算得到的湍流积分尺度分布形状类似，自相关函数能较好地满足指数衰减率。

(3) 自相关函数积分法和指数衰减拟合法均是基于Taylor假定，前者在稳定性方面优于后者，通过其计算得到的纵向湍流积分尺度随着平均时距的增大而增大，说明平均时距对湍流积分尺度是有影响的。当时距为5 min时采用自相关函数积分法计算得到的积分尺度较大，变异系数最小，分布最为集中。并且此时距下得到的平均风速较大，且湍流度和阵风因子较小。故可认为当平均时距为5 min时采用自相关函数积分法计算得到的湍流积分尺度较为合理。

[1]庞加斌,林志兴,葛耀军.浦东地区近地强风特性观测研究[J].流体力学实验与测量,2002,30(2):65-72.

[2]李家亮.基于近地观测的登陆台风湍流积分尺度研究[D].哈尔滨:哈尔滨工业大学,2012.

[3]王旭,黄鹏,顾明.基于台风“梅花”的近地层湍流积分尺度实测分析[J].同济大学学报,2012,40(10):1491-1497.

[4]胡尚瑜,李秋胜,黄建平.台风作用下低矮房屋屋面角部峰值压力实测研究[J].土木工程学报,2012,45(8),15-24.

[5]Simiu E,Scanlan R H.Wind effects on structure[M].New York:Wiley,1996.

[6]Flay R G J,St evenson D C .In tegral length scales in strong winds below 20 m[J].Journal of Wind Engineering and Industrial Aerodynamics,1998,28:21-30.

[7]庞加斌,葛耀军,陆烨.大气边界层湍流积分尺度的分析方法[J].同济大学学报,2002,30(5):622-626.

[8]刘欢,吴超羽,许炜铭.珠江河口底边界层湍流积分尺度研究[J].海洋工程,2008,26(4):125-131.

[9]宋丽莉.登陆台风近地层湍流特性观测分析[J].气象学报,2005,63(6),915-921.

[10]GB 50009-2012.建筑结构荷载规范[S].北京:中国建筑工业出版社,2012.

[11]陈雯超,宋丽莉,植石群,等.不同下垫面的热带气旋强风阵风系数研究[J].中国科学:技术科学,2011,41(11):1449-1459.

[12]Davenport A G.The spectrum of horizontal gustness near the ground in high winds[J].Q J R Meteorol Soc,1961,87:194-211.

Studyontyphooncharacteristicsathighurbanlandformaltitudeandturbulenceintegrallengthscale

WANG Chequan,LI Zhengnong*,HU Jiaxing,ZHANG Xuewen,ZHOU Lifen,CAO Shoukun

(KeyLaboratoryofBuildingSafetyandEfficiencyoftheMinistryofEducation,HunanUniversity,Changsha410082,China)

Based on the actually measured wind field materials about No.10 Typhoon,namely Matmo,from high urban-landform altitude in 2014,the data were analyzed in five time intervals (30 s,1 min,5 min,10 min and 20 min respectively),and strong wind characteristics were obtained with respect to the averaged wind speed,the wind direction,the turbulence intensity,the gust factor,and the fluctuating wind spectrum.The turbulence integral scale was then calculated with two methods based on Taylor assumption to investigate the effects of time intervals on the turbulence integral scale regarding the averaged wind speed,the turbulence intensity,and the gust factor.The results show that the averaged wind speed is the highest when the average time interval is 5 min.However,the turbulence intensity,the wind gust factor,and the corresponding variances and coefficients of variation are the smallest.These results are reasonable due to the densest calculated distributions of turbulence integral scale and the lowest variance gained by self-correlation function integral method.

turbulence characteristics; autocorrelation function; exponential decay rate; integral scale

0258-1825(2017)06-0801-07

TU312+.3

A

10.7638/kqdlxxb-2015.0090

2015-07-20;

2015-09-14

国家自然科学基金重大研究计划(91215302);国家自然科学基金(51478179,51178180).

王澈泉(1989-),男,博士研究生,主要从事高层结构抗风研究.E-mail:wangchequan@126.com

李正农*(1962-),男,工学博士,教授,主要从事建筑物抗震抗风研究等.E-mail:zhn88@263.net

王澈泉,李正农,胡佳星,等.城市地貌高空台风特性及湍流积分尺度的研究[J].空气动力学学报,2017,35(6):801-806,822.

10.7638/kqdlxxb-2015.0090 WANG C Q,LI Z N,HU J X,et al.Study on typhoon characteristics at high urban landform altitude and turbulence integral length scale[J].Acta Aerodynamica Sinica,2017,35(6):801-806,822.