基于阶频谱相关组合切片能量和SVM的滚动轴承故障诊断

汪治安，夏均忠，白云川，刘鲲鹏，吕麒鹏

(1.陆军军事交通学院 研究生管理大队，天津 300161；2.陆军军事交通学院 军用车辆系，天津 300161)

基于阶频谱相关组合切片能量和SVM的滚动轴承故障诊断

汪治安1，夏均忠2，白云川2，刘鲲鹏1，吕麒鹏1

(1.陆军军事交通学院 研究生管理大队，天津 300161；2.陆军军事交通学院 军用车辆系，天津 300161)

针对变转速工况下滚动轴承故障诊断问题，提出基于阶频谱相关组合切片能量(SEOFSC)和支持向量机(SVM)的滚动轴承故障诊断方法。首先研究阶频谱相关(OFSC)对滚动轴承故障特征提取的原理；其次针对OFSC的不足，计算振动信号阶频谱相关组合切片以提高故障特征提取效率，对其谱频率轴积分得到SEOFSC实现故障特征降维；最后选取切片簇中能量极大值构成特征向量输入到“一对一”多分类SVM中进行故障模式识别。通过对比试验表明，该方法可以实现变转速工况下滚动轴承快速、准确的故障诊断，具有一定的工程实用价值。

滚动轴承；故障诊断；角度/时间循环平稳；阶频谱相关组合切片能量；支持向量机(SVM)

v

滚动轴承广泛应用于各类机械设备中，其工作状态直接影响整台机械设备的性能。在高速重载的环境下，滚动轴承容易失效[1]。对滚动轴承的故障诊断方法的研究一直是国内外研究的热点[2-3]。

实际运行过程中，大多数机械通常工作在速度波动较大的变转速工况下[4]，滚动轴承故障振动信号出现复杂的频率、幅值和相位调制等现象[5-6]。为此，Abboud等[7-8]在循环平稳的基础上，提出了角度/时间循环平稳(angle/time cyclostationary, AT-CS)，利用阶频谱相关(order-frequency spectral correlation, OFSC)表征变转速下滚动轴承故障特征，为循环平稳在变转速工况下的滚动轴承故障诊断奠定了基础。

OFSC存在两点不足[9-10]：①计算量大。为较好地从信号中提取滚动轴承故障特征，在估计信号的阶频谱相关时，需要保证较高的阶次分辨率和足够的阶次范围，从而使得遍历的循环阶次数目增多，计算量较大。②特征表达不直观，维数较高。OFSC是通过三维图的方式表征变转速工况下滚动轴承故障特征，在噪声干扰下，难以从图中准确识别故障特征阶次。

Vapnik等[11]提出的支持向量机(support vector machine, SVM)算法为基于结构风险最小化方法的统计学习理论，具有很强的学习和泛化能力，能够较好地解决小样本、非线性、高维数等模式识别问题[12]。在滚动轴承的故障诊断中，由于采集的故障样本数量有限，因此SVM被广泛应用于滚动轴承故障诊断。明阳等[13]将谱相关密度切片分析与SVM相结合实现滚动轴承故障诊断。张小龙等[14]提取ITD分解后PR分量的Lempelk-Ziv复杂度构建特征向量，将其输入到SVM中实现滚动轴承不同类型故障模式识别。

本文在研究阶频谱相关的基础上，提出基于阶频谱相关组合切片能量(sliced energy of order-frequency spectral correlation，SEOFSC)和支持向量机的滚动轴承故障诊断方法。通过计算信号的阶频谱相关组合切片，减少计算量，提高特征提取效率；对阶频谱相关组合切片的谱频率轴积分得到SEOFSC，降低故障特征维数；从SEOFSC中选择局部能量极大值组成特征向量输入到SVM中进行模式识别，实现滚动轴承故障诊断。

1 特征提取

1.1 阶频谱相关(OFSC)

变转速工况下，滚动轴承点蚀故障具有如下特点：故障产生的冲击不再具有时域周期性，由于轴承是旋转对称结构，相邻两次冲击间隔的角度不变，因此其故障冲击仍具有角域周期性；同时，故障冲击依然随时间衰减，故其脉冲响应在时域描述最佳。称此类信号为角度/时间循环平稳信号(AT-CS)。

为实现变转速工况下的滚动轴承故障特征提取，需要建立一个既能够表征信号的角域周期性，又能够描述时域脉冲响应的统计量。将传统循环统计量从时域转化到角度/时间域，此时其角度/时间自相关函数(angle/time autocorrelation function，ATCF)具有周期性：

R2x(τ，θ)=E{x(t(θ))·x(t(θ))-τ)*}=

R2x(τ，t(θ))

(1)

式中：τ为时间延迟；E为集总平均运算。

时间t和角位移θ存在下列关系：

(2)

式中ω(t)为瞬时角速度。

定义ATCF的二次傅里叶变换为阶频谱相关(OFSC)：

(3)

式中α为循环阶，对于滚动轴承故障诊断，可视为参考轴每旋转一周故障冲击产生的次数。

对于AT-CS信号，其OFSC具有如下性质：

(4)

阶频谱相关是谱频率f和循环阶α的函数，在α—f平面内，存在一系列垂直于α轴的谱线，谱线对应信号的循环特征阶次及其谐波成分，谱线的幅值主要集中在信号的响应频带上。根据阶频谱相关的这个特点，可以有效提取滚动轴承振动信号中的AT-CS成分，进行故障诊断。

1.2 阶频谱相关组合切片能量

为克服阶频谱相关在计算效率和特征表达方面的不足，分别从两方面对其进行改进。

为降低阶频谱相关的计算量，将组合切片思想与阶频谱相关估计相结合。根据滚动轴承的几何参数，选择外圈、内圈、滚动体的理论故障特征阶次及其前3个倍频，计算相应的阶频谱相关组合切片，通过切片之间的能量对比能够初步判断轴承的故障状态，称该方法为阶频谱相关组合切片分析。为降低故障特征的维数，在滚动轴承的故障诊断中，只提取能够反映调制特征的阶次信息，而忽略载频信息。对阶频谱相关组合切片方法进一步改进，将信号的阶频谱相关组合切片的谱频率轴积分得到阶频谱相关组合切片能量，选取切片簇中能量极大值作为该特征循环频率对应的切片能量，将故障特征从三维降低到二维。

基于阶频谱相关组合切片能量(SEOFSC)的故障特征提取流程如图1所示，其主要步骤包括：

(1)由滚动轴承的瞬时转速曲线积分得到角位移曲线；

(2)根据滚动轴承的结构参数计算理论故障特征阶次，并以理论故障特征阶次及其前3个倍频作为组合切片中心，选择一定的切片宽度，并由此确定切片区间；

(3)利用平均循环周期图法计算振动信号在切片区间的OFSC，得到阶频谱相关组合切片；

(4)选取合适的积分频带对阶频谱相关组合切片的谱频率轴积分得到SEOFSC，降低故障特征的维数；

(5)对于每一个切片簇，选取其中能量极大值作为该切片中心对应的能量值，将所有切片中心对应的能量值构成故障特征向量。

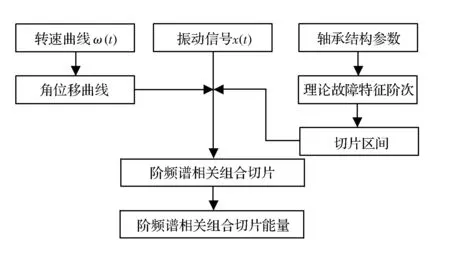
图1 轴承故障特征提取流程

2 支持向量机(SVM)

2.1 SVM分类原理

对于线性可分的训练样本集，Q={(xi,yi)|xi∈Rn，yi∈{-1，1}，i=1,2,…，l}，存在超平面H使得训练样本中的两类输入分别位于H的两侧。

H:wTx+b=0

(5)

式中：wT为分类面权向量；b为分类阈值。

满足式(5)条件的超平面并不唯一，需要寻找一个最优超平面，使得所有样本到超平面的距离最大，尽量减小分类误差，实现结构风险最小化。

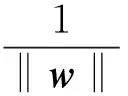
(6)

式(6)是一个带线性不等式约束的二次规划问题，为此，定义Lagrange函数：

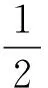
(7)

式中βi为Lagrange系数。

f(x)=sgn {wTx+b}

(8)

以上分析是对于线性可分样本，对于线性不可分样本，利用核函数K(xi，yi)将样本非线性映射到高维空间，在高维空间寻找最优超平面。为允许一定程度的错分，引入非负松弛变量ξi和惩罚因子C，将最优分类面的约束条件变为

(9)

式中，松弛变量ξi指出了离群点的离群程度，值越大，离群越远。惩罚因子C则决定了在多大程度上重视离群点带来的危害，其值越大，重视程度越高。

此时，最优分类函数为

(10)

典型核函数有线性核函数、多项式核函数和高斯径向基核函数，3种核函数的表达形式如下：

(11)

2.2 多分类SVM

SVM本质上是两分类的分类器，实际应用中轴承故障类型多于两类，因此需要构造合适的多分类器。通过组合多个二分类SVM，可以实现多分类器构造，常用方法有“一对多”“一对一”“二叉树”等方法。其中“一对一”方法，是指训练时为任意两类样本构造一个分类器，N个类别所需SVM分类器数量为N(N-1)/2。将待分类样本输入到每个两类分类器中，统计每个分类器的分类结果，用“投票法”决定待分类样本的所属类别。这种方法具有训练和识别速度快的特点，但是随着类别数的增加，需要构造的二分类数目会急剧上升(类别数的平方级别)，使得训练过程速度变慢。由于滚动轴承的故障类型有限，需要构造的二分类数目较少，因此本文采用“一对一”的方法实现SVM多分类模式识别。

3 轴承故障诊断

基于OFSC组合切片能量与SVM的轴承故障诊断流程如图2所示。

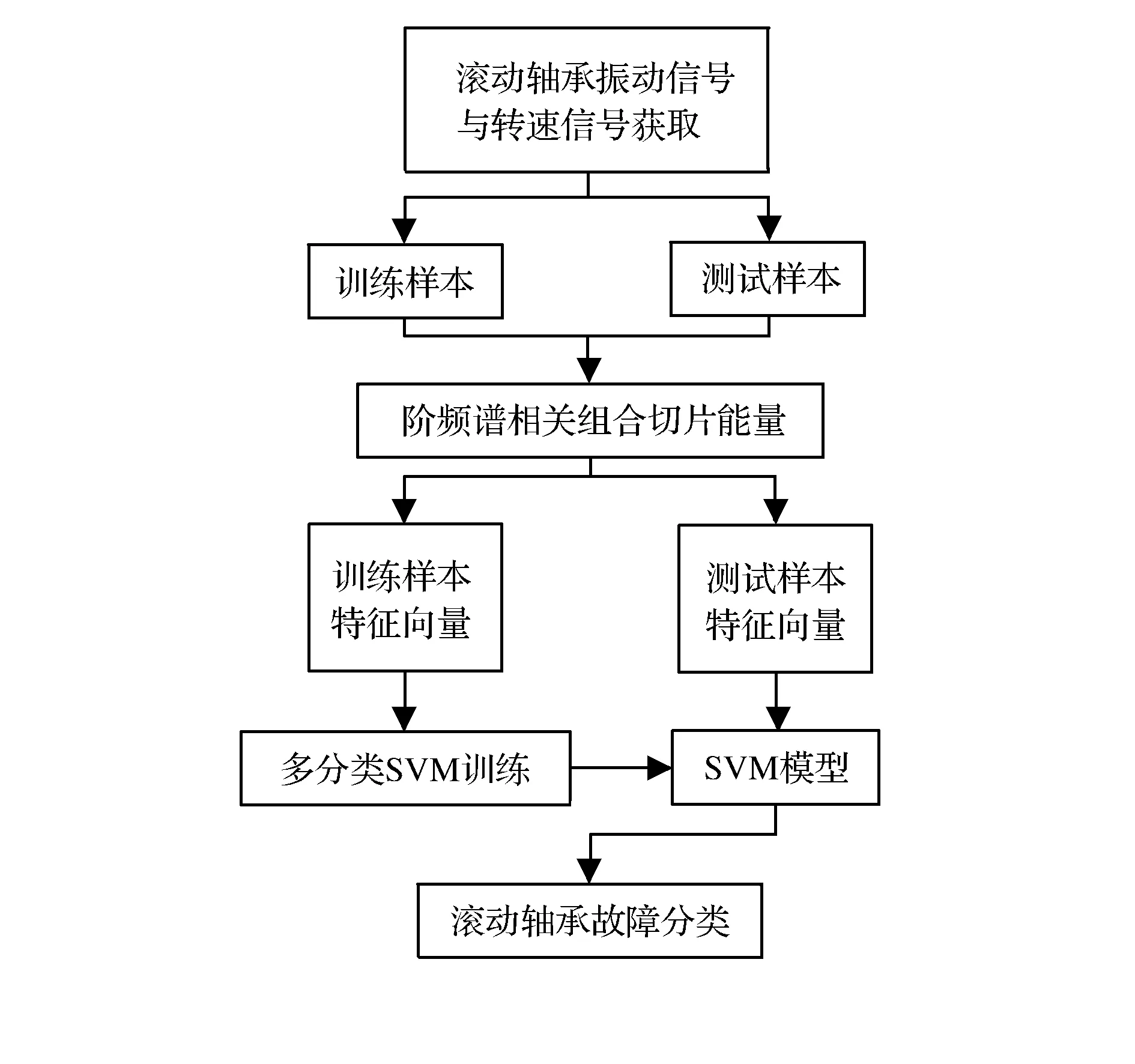
图2 轴承故障诊断流程

采集不同故障类型的滚动轴承振动信号及其转速信号，将其分为训练样本和测试样本。计算各个样本的阶频谱相关组合切片能量，选取每个切片簇中能量极大值作为切片对应的能量值，构成特征向量。将训练样本的特征向量及其对应的故障类型输入到多分类SVM中进行训练，得到SVM模型。将测试样本的特征向量输入到训练好的SVM模型中，根据SVM模型识别的结果与测试样本对应的故障类型进行比对，判断SVM故障诊断的准确性。

4 试验验证

试验装置主要由三相驱动电机、变频控制器、驱动轴、从动轴等组成[15]。通过变频器控制电机转频在10～20 Hz之间，采样频率为50 kHz，采样时长为21 s。

试验轴承安装在从动轴上，其主要技术参数见表1。分别在3个轴承上加工外圈、内圈、滚动体故障，故障截面形状为正方形，深度为1 mm，边长为3 mm。根据表1中的技术参数计算得到滚动轴承的理论故障特征阶次，外圈故障特征阶次BPO=3.592，内圈故障特征阶次BPI=5.409，滚动体故障特征阶次BPB=0.399。

表1 试验轴承技术参数

不同故障轴承试验的转速曲线和振动信号时域波形，分别如图3、图4所示。3种故障状态的转频变化均在10～15 Hz，其对应的转速差最大可达300 r/min，说明转速变化较快，且都经历了加速和减速过程，速度变换也较为复杂。3种故障振动信号的幅值受到转速的调制，从中无法识别出故障类型。

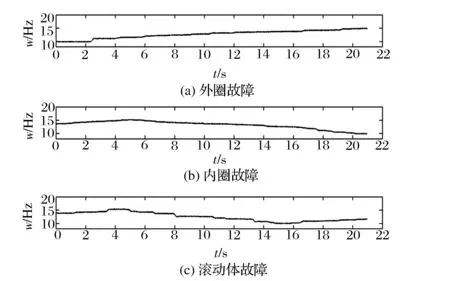
图3 试验轴承运行转速曲线

以外圈故障特征为例，介绍基于阶频谱相关组合切片能量的故障特征提取过程。对瞬时转速曲线积分得到角位移曲线如图5所示。

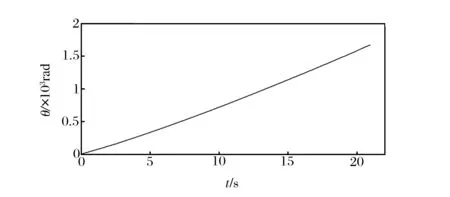
图5 外圈故障轴承角位移曲线

根据滚动轴承理论故障特征阶次及其二、三倍频确定切片中心αT=[BPB, 2BPB, 3BPB,BPO,BPI, 2BPO, 3BPO,2BPI,3BPI](按升序排列)，以Δα=0．05作为切片宽度，确定组合切片区间。计算组合切片区间对应的阶频谱相关，得到外圈阶频谱相关组合切片(如图6所示)。

通过观察图6中阶频谱相关，发现其能量主要集中在10～500 Hz，故以此为积分频带对阶频谱相关组合切片的谱频率轴积分得到阶频谱相关组合切片能量(如图7所示)。

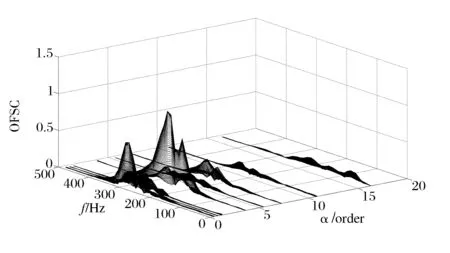
图6 外圈故障阶频谱相关组合切片

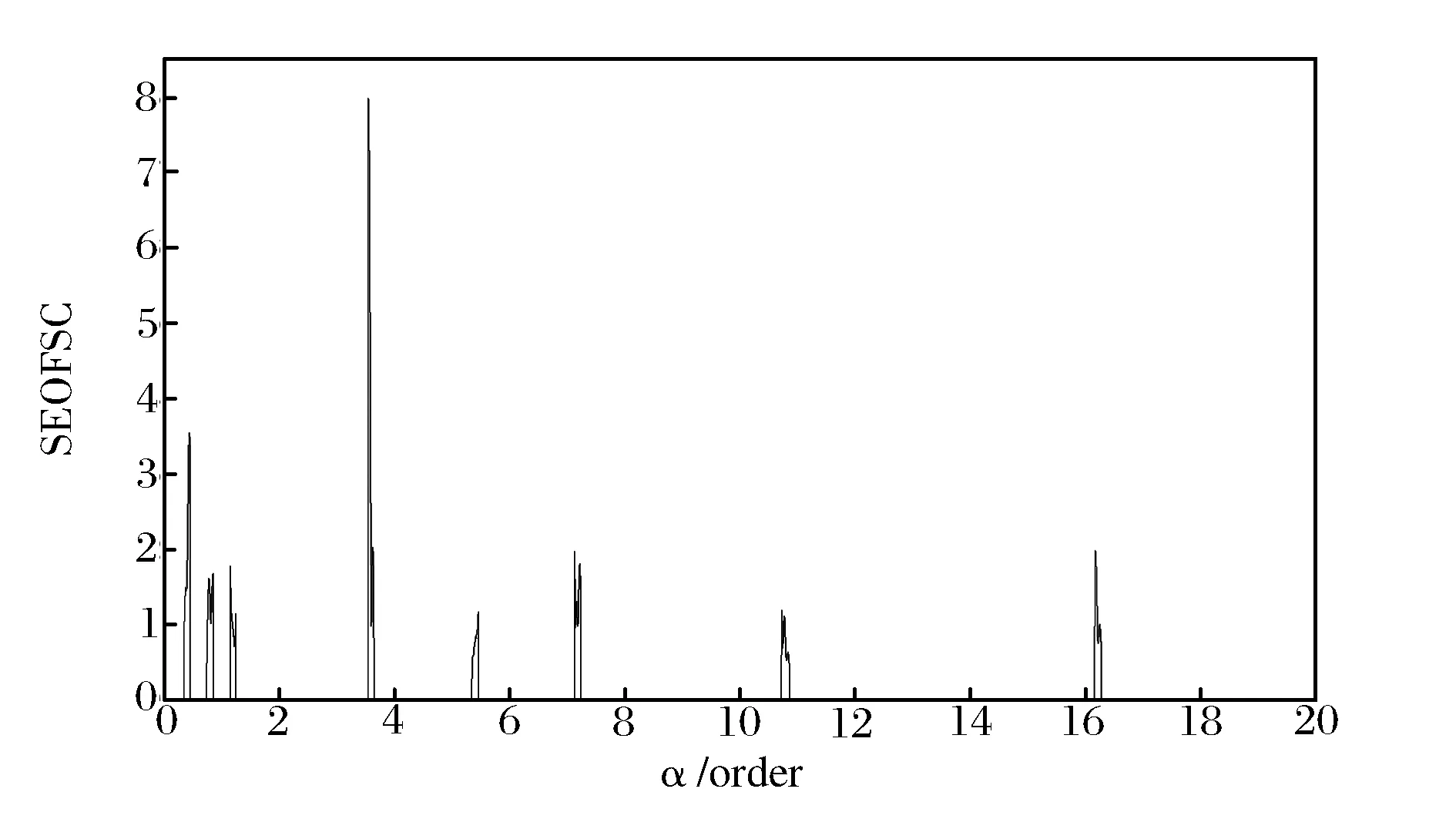
图7 外圈故障阶频谱相关组合切片能量

从阶频谱相关组合切片能量中提取特征向量。分别提取各切片簇中能量极大值作为切片中心对应的能量值，得到外圈故障信号的故障特征向量，同理，可得到内圈和滚动体故障对应的特征向量，3种故障对应的特征向量见表2。对于某一具体故障类型的特征向量，其理论故障特征阶次及其谐波处对应的幅值较大，不同故障类型之间的特征向量差异性较大。

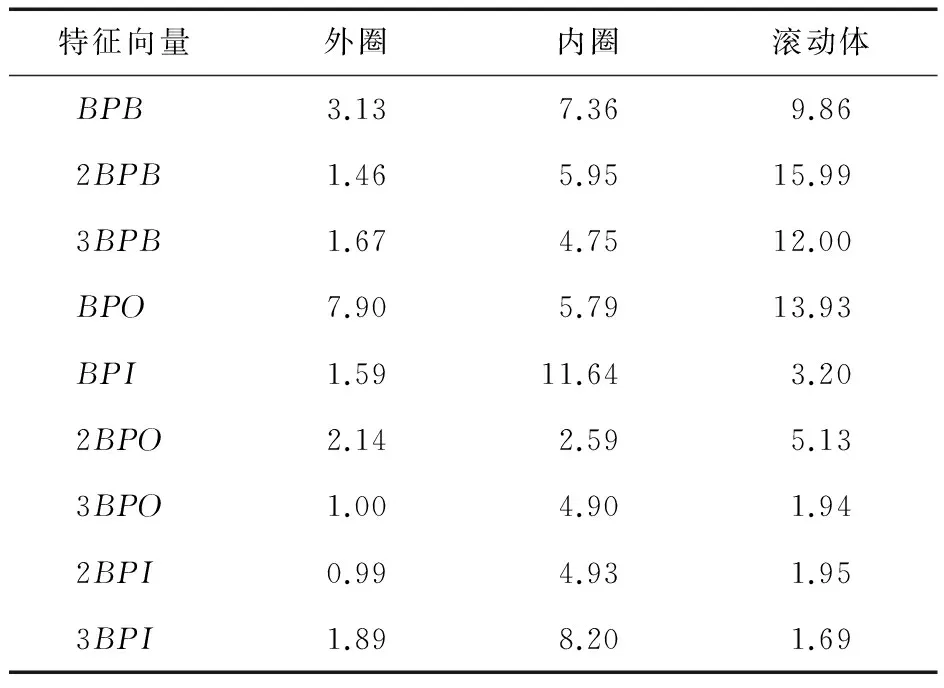
表2 故障特征向量

单个样本的规律难以说明特征向量的稳定性，为研究故障特征向量的一致性，提取不同故障多个样本的特征向量进行了比较分析。分别提取外圈、内圈和滚动体故障各30组样本的特征向量，得到不同样本特征向量的分布图(如图8所示)。同时计算同一故障的不同特征向量之间的平均相关系数，外圈、内圈、滚动体故障特征向量之间的平均相关系数分别为0.98、0.83、0.97，说明同种故障向量之间的故障特征向量高度相关，结合图8可以看出，对于同一种故障类型，其故障特征向量具有较好的鲁棒性。

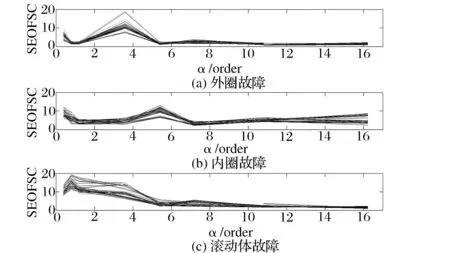
图8 不同故障特征向量分布

试验所用训练样本从数据集中随机抽取，外圈、内圈、滚动体故障数据各选30组，每组100 000个数据点，共90组训练样本，用于训练SVM。用同样的方法得到90组测试样本，用于测试SVM模型识别故障类型的准确性。

用类别Ⅰ表示外圈故障，类别Ⅱ表示内圈故障，类别Ⅲ表示滚动体故障。为测试SVM分类的准确性，分别用30、60、90组测试样本对其进行验证，其预测准确率见表3。说明通过多分类SVM可以准确识别滚动轴承的故障类型。

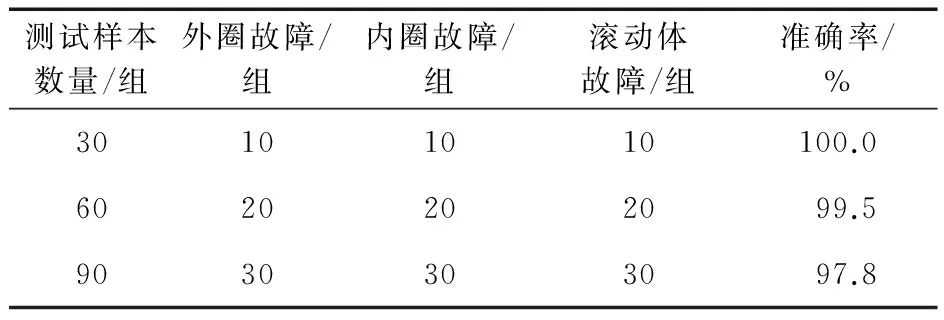
表3 不同样本数量识别结果

5 结 论

(1)针对阶频谱相关在计算效率和特征表达上的不足，分别从两方面对其改进，提出基于阶频谱相关组合切片能量的特征提取方法，将组合切片思想融入到阶频谱相关估计，得到阶频谱相关组合切片，对其谱频率轴积分得到相应的阶频谱相关组合切片能量。较之于阶频谱相关方法，具有计算效率高，特征维数低的特点。

(2)选取阶频谱相关组合切片簇中能量极大值构成特征向量，该特征向量不受转速变化的影响，具有较好的鲁棒性。

(3)利用支持向量机结构风险最小化的优点，将阶频谱相关组合切片能量与“一对一”多分类SVM相结合实现变转速工况下滚动轴承故障诊断，实测数据表明该方法能够准确识别滚动轴承的外圈、内圈、滚动体故障。

[1] 夏均忠,赵磊,白云川,等.基于Teager能量算子和ZFFT的滚动轴承故障特征提取[J].振动与冲击,2017,36(11):106-110.

[2] 汪治安,夏均忠,但佳壁,等.循环平稳在滚动轴承故障诊断中的应用[J].军事交通学院学报,2017,19(6):25-30.

[3] RANDALL R B，ANTONI J. Rolling element bearing diagnostics: a tutorial[J].Mechanical Systems and Signal Processing, 2011,25(2): 485-520.

[4] ABBOUD D, ANTONI J, SIEG-ZIEBA S, et al. Envelope analysis of rotating machine vibrations in variable speed conditions: a comprehensive treatment[J]. Mechanical Systems and Signal Processing, 2017, 84:200-226.

[5] 林京,赵明.变转速下的机械设备动态信号分析方法的回顾与展望[J].中国科学(技术科学),2015,45(7):669-686.

[6] ANTONI J, GRIFFATON J, ANDRE H, et al. Feedback on the surveillance 8 challenge: vibration-based diagnosis of a safran aircraft engine[J]. Mechanical Systems and Signal Processing, 2017,97:1112-144.

[7] ABBOUD D, ANTONI J, ELTABACH M, et al. Angle/time cyclostationarity for the analysis of rolling element bearing vibrations[J]. Measurement, 2015,75:29-39.

[8] SOPHIE B, DIDER R, ANTONI J, et al. Non-intrusive rattle noise detection in non-stationary conditions by an angle/time cyclostationary approach[J]. Journal of Sound and Vibration, 2016, 366:501-513.

[9] ANTONI J，XIN G，HAMZAOUI N. Fast computation of the spectral correlation[J]. Mechanical Systems and Signal Processing, 2017, 92: 248-277.

[10] 毕果,陈进.组合切片分析在滚动轴承故障诊断中的应用研究[J].机械科学与技术,2009,28(2):182-185.

[11] VAPNIL V N.The nature of statistical learning theory[M].New York:Springer-Verlag,1995:92．

[12] LIU Y, BI J W, FAN Z P. A method for multi-class sentiment classification based on an improved one-vs-one (OVO) strategy and the support vector machine (SVM) algorithm[J]. Information Sciences, 2017, 394-395:38-52.

[13] 明阳,陈进.基于谱相关密度切片分析和SVM的滚动轴承故障诊断[J].振动与冲击, 2010,29(1):196-199.

[14] 张小龙,张氢,秦仙蓉,等.基于ITD复杂度和PSO-SVM的滚动轴承故障诊断[J].振动与冲击, 2016,35(24):102-107.

[15] MISHRA C，SAMANTARAY A K，CHAKRABORTY G，et al. Rolling element bearing defect diagnosis under variable speed operation through angle synchronous averaging of wavelet de-noised estimate[J]. Mechanical Systems and Signal Processing, 2016,72-73:206-222.

RollingBearingFaultDiagnosisBasedonSEOFSCandSVM

WANG Zhian1, XIA Junzhong2, BAI Yunchuan2, LIU Kunpeng1, LYU Qipeng1

(1.Postgraduate Training Brigade, Army Military Transportation University, Tianjin 300161, China;2.Military Vehicle Department, Army Military Transportation University, Tianjin 300161, China)

Considering the fault diagnosis problem of rolling bearing under variable speed condition, the paper proposes a fault diagnosis method of rolling bearing based on sliced energy of order-frequency spectral correlation (SEOFSC) and support vector machine (SVM). Firstly, it studies the principle of order-frequency spectral correlation (OFSC) on bearing fault feature extraction. Then, it calculates combined slices of OFSC to improve the efficiency of fault feature extraction, and obtains SEOFSC by integrating the spectral frequency axis to reduce the fault feature dimension. Finally, it selects maximal values from slice cluster to compose feature vector and input it into “one-to-one” multi-classification SVM for fault pattern recognition. The experimental indicate that the proposed method can realize rapid and accurate fault diagnosis of the rolling bearing under the variable speed condition, and it has some practical value in engineering.

rolling bearing; fault diagnosis; angle/time cyclostationary; sliced energy of order-frequency spectral correlation(SEOFSC); support vector machine(SVM)

2017-08-30；

2017-09-12.

汪治安(1992—)，男，硕士研究生；

夏均忠(1967—)，男，博士，教授，硕士研究生导师.

10.16807/j.cnki.12-1372/e.2017.12.007

TH133.33；TP206+.3

A

1674-2192(2017)12- 0029- 06

(编辑：张峰)