六自由度地震模拟试验台运动轨迹规划
翟 华 ,朱晓锋 ,丁 煦 ,3,左根明
(1.合肥工业大学工业与装备技术研究院,安徽 合肥230009;2.合肥工业大学机械与汽车工程学院,安徽 合肥 230009;3.航空结构件成形制造与装备安徽省重点实验室,安徽 合肥 230009;4.安徽新视野科教文化股份有限公司,安徽 铜陵 244000)
六自由度地震模拟试验台运动轨迹规划
翟 华1,2,3,朱晓锋1,丁 煦1,3,左根明4
(1.合肥工业大学工业与装备技术研究院,安徽 合肥230009;2.合肥工业大学机械与汽车工程学院,安徽 合肥 230009;3.航空结构件成形制造与装备安徽省重点实验室,安徽 合肥 230009;4.安徽新视野科教文化股份有限公司,安徽 铜陵 244000)
本文以六自由度地震模拟试验台为研究对象,构建了位姿反解模型。提出了一种六自由度地震模拟试验台运动轨迹规划方法,通过位姿反解模型推导出了六自由度地震模拟试验台与手动六自由度平台之间关节空间和工作空间的相似关系。利用相似性关系获得六自由度地震模拟试验台驱动缸的运动方程,实现对手动六自由度平台的运动过程再现。建立了六自由度地震模拟试验台与手动六自由度平台仿真模型,仿真实验结果验证了相似结构六自由度平台之间驱动缸和上平台的运动特性曲线关系。为六自由度地震模拟试验台的控制系统的设计提供参考。
六自由度平台;轨迹规划;虚拟样机;运动学仿真
地震模拟试验台是依据地震波运动机理,模拟地震时地面的剧烈抖动、摇晃运动形式的专用实验仪器。国外在上世纪40年代开始将地震模拟平台应用在土木工程实验领域[1],80年代以后,我国也开始研究开发地震模拟运动平台,主要采用液压驱动模拟平面运动[2],尚未具备模拟高烈度地震时出现的复杂空间地震波功能。为了模拟不同级别和烈度的P-波、S-波、地表波和混合地震波等复杂地震波,再现地震时地面的运动情况,同时具备多自由度运动、重载、动作响应快的特点,国际上主要采用六自由度并联运动平台模拟实现复杂地震波。
本文提出一种六自由度地震模拟试验台的轨迹规划方法,通过构建结构相似的地震模拟试验台,依据其工作空间的相似性关系,实现结构相似平台的运动传递再现过程。经过地震模拟试验台仿真和现场试验,仿真结果和实验结果验证了结构相似的六自由度平台之间驱动缸和上平台运动特性曲线的关系,实现了大型六自由度地震模拟试验台轨迹规划。为六自由度模拟试验台控制系统设计提供参考。
1 构建手动六自由度平台与地震模拟试验台
如图1所示为手动六自由度平台,每条支路由直线位移传感器和两个球铰相连而成。

图1 手动六自由度平台
通过采集小型手动六自由度平台的位移传感器信号,生成给定轨迹上的若干个点,对轨迹数据进行判断,采集数据是否符合地震波运动特征。
当采集数据符合需要模拟的地震波级别和烈度要求,并以速度、加速度为约束条件,将六自由度平台驱动轴轨迹上的位置值进行缩放,然后在关节空间中的相应点建立运动方程,获得大型六自由度地震模拟试验台关节空间运动方程。

图2 六自由度地震模拟试验台
如图2所示为大型六自由度地震模拟试验台,每条支路都是由一个电动伸缩缸和两个胡克铰连接而成。
为了能真实再现手动六自由度平台的运动模式,大型六自由度地震模拟试验台的运动机构采用与手动六自由度平台相同的Stewart平台。通过构建试验台和平台位姿反解模型,推导出两Stewart平台关节空间与工作空间运动特性的相似性关系。将小型手动六自由度平台运动信息克隆转载到大型六自由度地震模拟试验台上,实现对大型六自由度地震模拟试验台的运动控制。
大型六自由度地震模拟试验台是由六个电动伸缩缸共同驱动上平台,各电动伸缩缸协调一致地动作,才能保证运动过程中的稳定性。
大型六自由度地震模拟试验台控制目标不仅有轨迹规划和点位控制要求,还要兼顾中间过程,不仅要实现到达目标点的准确性和快速性,还要保证点与点之间生成的目标轨迹是平滑的轨迹。
2 地震模拟试验台上平台位姿反解模型
如图3所示,为了描述大型六自由度地震模拟试验台的各铰接点空间位置关系及平台运动姿态,定义六自由度地震模拟试验台的结构参数,上铰接点外接圆半径Ra;下铰接点外接圆半径Rb;工作初始位置时电动伸缩缸长度l0;上铰接点之间的最短距离;下铰接点之间的最短距离db;在上平台建立动坐标系O1-X1Y1Z1,下平台建立静坐标系O-XYZ。上平台Ai和下平台的Bi(i=1,2,…,6)通过电动伸缩缸连接,其中O1、O分别与上、下平台的质心重合。
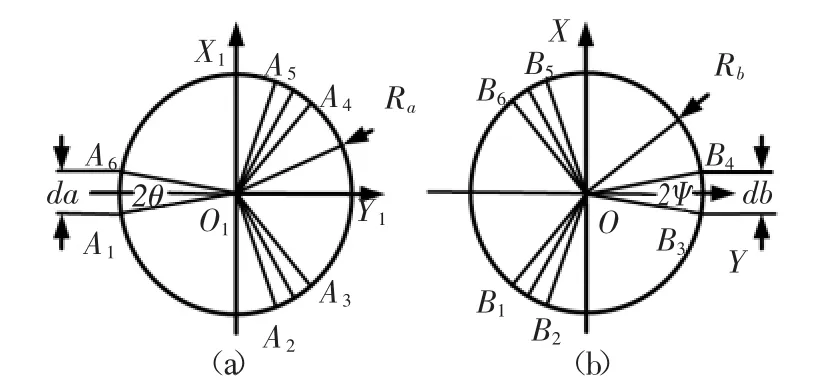
图3 连接点的位置分布(a)上平台 (b)下平台
为了描述上平台各点在固定坐标系下位姿,需建立一个局部坐标系与固定坐标系之间的齐次变换矩阵。γ、β、α分别代表由局部坐标系到固定坐标系依次绕Z轴、Y轴和X轴转动的滚动角、俯仰角、偏航角。依次绕Z轴、Y轴和X轴旋转变换,可以得到由局部坐标系到固定坐标系的坐标变换矩阵T为[12]:
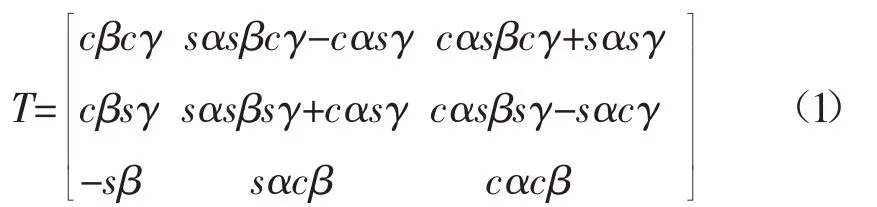
式中:sα——表示sin(α);
cα——表示cos(α);
sβ、cβ、sγ、cγ 等依此类推。
分别定义上、下平台的铰接点为Ai、Bi,其中Ai在局部坐标系{O1}中的坐标为 ,下铰点Bi在固定坐标系{O}中的坐标表示为Bi=(Bix,Biy,Biz);
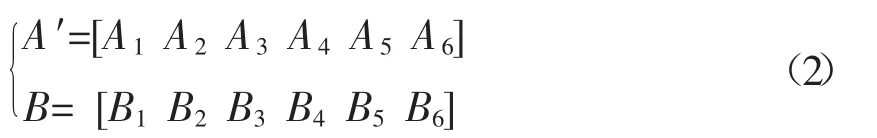
其中Ai、Bi在局部坐标系和固定坐标系的坐标为:
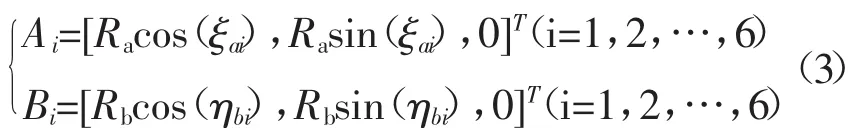
其中:
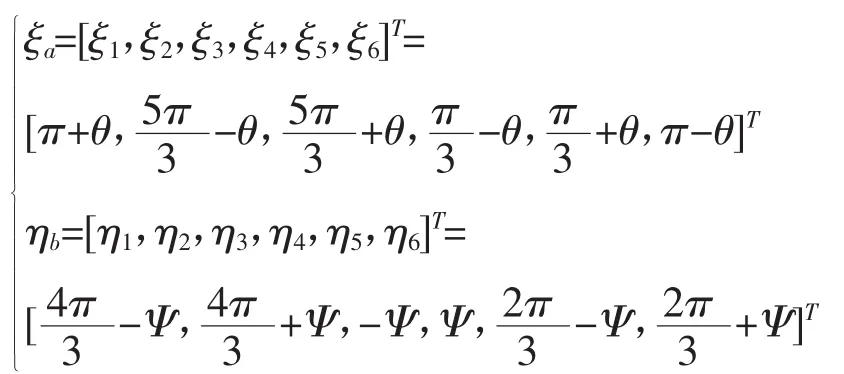
式中:θ——上平台短边所对应的圆心角的大小,
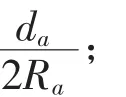
Ψ——下平台短边所对应的圆心角的大小,
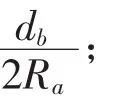
ai——上铰点在局部坐标系O1的位置矢量;
bi——下铰点在固定坐标系O的位置矢量;
ξi——在局部坐标系中从原点O1到上铰接点的连线与X1轴正方向夹角;
ηi——在固定坐标系中从原点O到上铰接点的连线与X轴正方向夹角。
Ai在静坐标系{O}中的坐标表示为 Ai=(Aix,Aiy,Aiz)。

当平台运动,上下平台铰接点之间的距离为l时,相应的计算公式为:
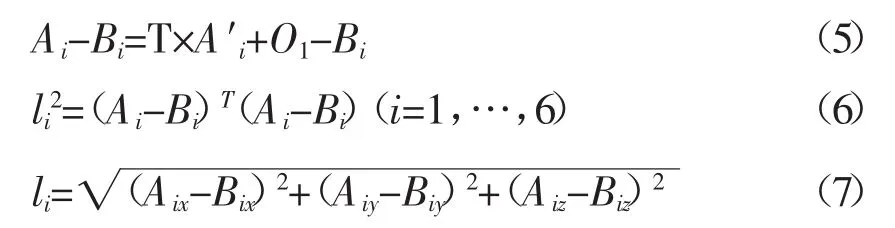
电动伸缩缸的伸缩量为:

式中:O1(x,y,z)(α,β,γ)——分别为沿x向、y向、z向平移的距离和绕x轴、y轴、z轴旋转的角度;
l0——零位时各驱动轴初始伸长量;
Δli——在某一时刻,确定的局部坐标系{O1}和固定坐标系{O},相对电动缸伸缩量。
3 地震模拟试验台轨迹规划分析
由于地震波的获取是由小型手动六自由度平台的位移传感器信号采集为基础,因此手动摇动过程中,奇异位形可以避免,上述三个假设可以成立。但在大型六自由度地震模拟试验台控制过程中,必须防止发出错误命令,避免出现奇异位形情况。
在大、小两个六自由度平台位移信号传递中,可以将小型手动六自由度平台运动信息克隆转载到大型六自由度地震模拟试验台上。
由于两平台结构相似,且手动六自由度平台与六自由度地震模拟试验台的结构尺寸比例为δ倍,设max对应大型地震模拟实验台尺寸下标,min对应手动六自由度平台下标,则两平台间对应的相似关系如下:
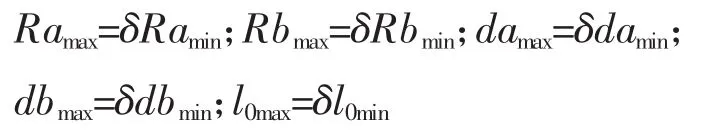
相应的两平台铰接点坐标:
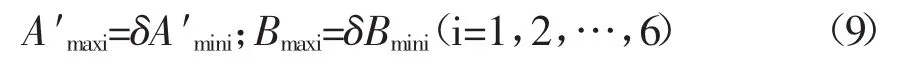
将手动六自由度平台、六自由度地震模拟试验台的结构基本参数代入式(11):

当 Δlmaxi=δΔlmini时,由平台结构参数和式(12)可得:

将式(13)、(16)代入式(15)中可得:
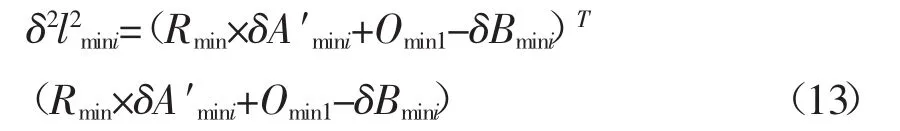
当 Rmax=Rmin;Omax1=δOmin1时,式(13)可化简为:
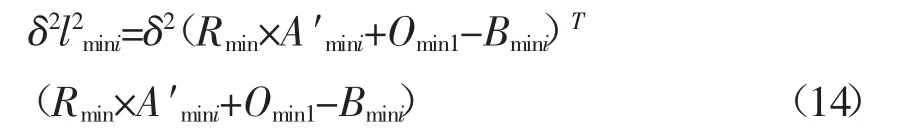
由式(12)、(13)、(14)可得,当六自由度地震模拟试验台和手动六自由度台驱动缸的变化量Δli成δ倍时,Rmax=Rmin;Omax1=δOmin1是其一组解,同时依据假设可知上平台位姿解的唯一性,可得当六自由度地震模拟试验台的各缸变化量与手动六自由度台驱动缸的变化量Δli成δ倍时,六自由度地震模拟试验台的位姿一定是 Rmax=Rmin;Omax1=δOmin1。
结合上述可知结构相似的六自由度地震模拟试验台和手动六自由度平台一定存在且唯一满足的位姿关系,

利用尺度压缩获得与六自由度地震模拟试验台结构相似的手动六自由度平台。首先通过手动六自由度平台对地震波传播形式进行运动模拟,获得6组驱动轴的运动信息,然后将其进行等比例放大后,通过加载控制六自由度地震模拟试验台的6组电动伸缩缸,实现了结构相似六自由度平台的运动过程再现。
4 实验验证
为了验证两六自由度平台的关节空间与工作空间的相似关系,首先确定六自由度地震模拟试验台的结构参数 Ramax;Rbmax;damax;dbmax;l0max,然后依据六自由度地震模拟试验台的结构参数进行δ倍的尺度压缩获得手动六自由度台的结构参数Ramin;Rbmin;damin;dbmin;l0min。根据六自由度地震模拟试验台和手动六自由度台的结构参数,在Creo Parametric中建立六自由度地震模拟试验台和手动六自由度台的三维模型。并导入ADAMS软件中,然后更改材料属性,添加约束、载荷、驱动。
首先对手动六自由度台进行运动模拟,得到复合运动时的各个位移传感器的运动位移曲线,利用后处理输出模块将各个位移传感器数据进行保存。将获得的位移曲线在MATLAB中放大δ倍,导入到Adams软件中,将位移曲线对应作为六自由度地震模拟试验台电动伸缩驱动缸的驱动函数,可以绘制出动平台的质心相对于固定坐标系的位姿曲线。
将上述的六自由度地震模拟试验台的位姿曲线与手动六自由度平台规定的位姿曲线在MATLAB中对比如图4、5,位姿关系也呈相似关系:
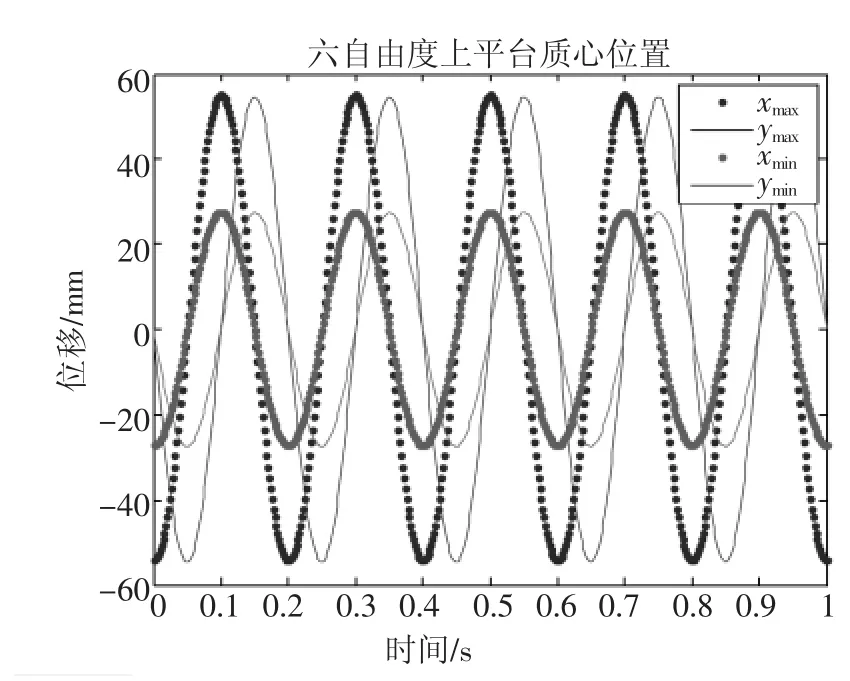
图4 手动六自由度台和六自由度地震模拟试验台动平台质心的位置曲线
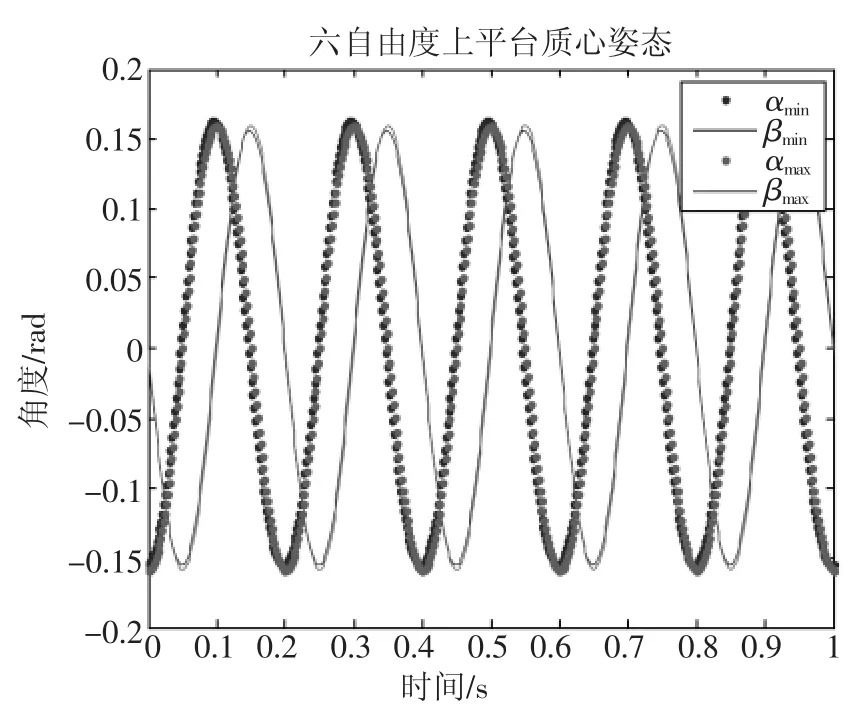
图5 手动六自由度台和六自由度地震模拟试验台动平台质心的姿态曲线
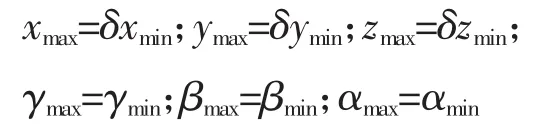
将获得的各轴位移曲线利用正解算法求得各平台的运动轨迹,通过测量小六自由度平台的位移曲线和电动缸的位移曲线,获得它们上平台位置曲线与姿态曲线对比图。如图6、7所示。
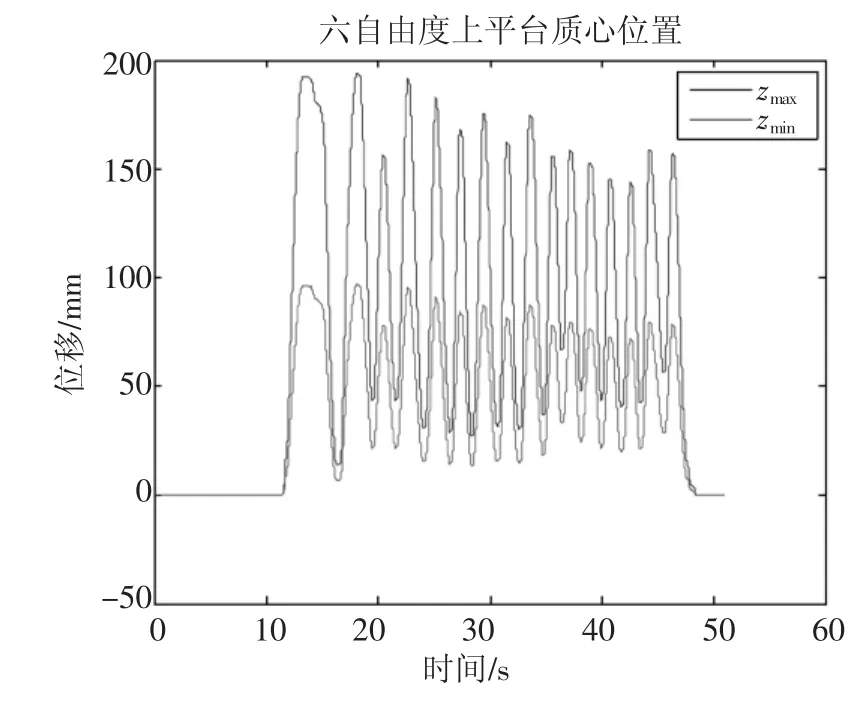
图6 手动六自由度台和六自由度地震模拟试验台动平台质心沿Z轴的位置曲线
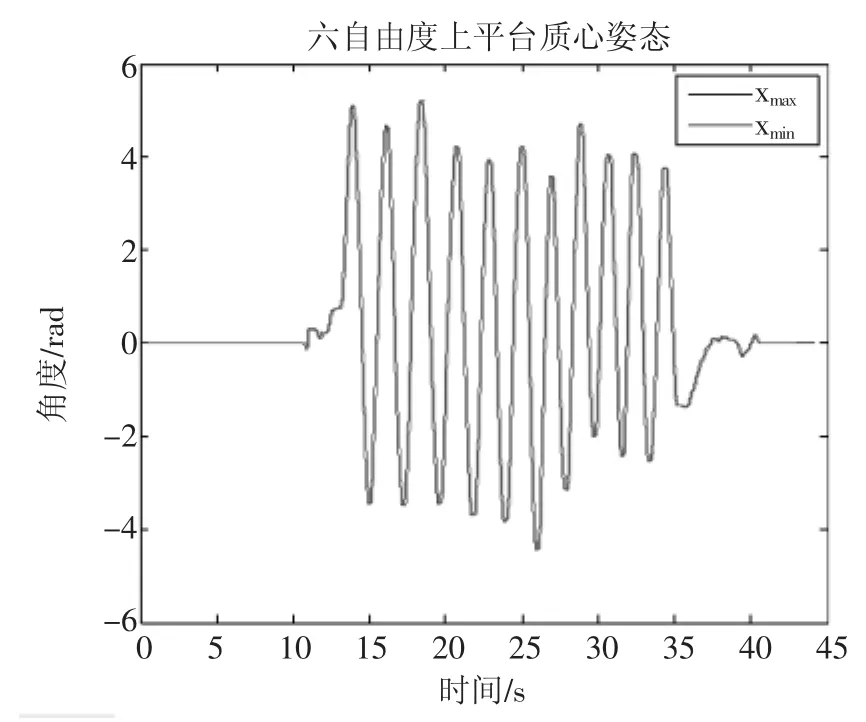
图7 手动六自由度台和六自由度地震模拟试验台动平台质心绕X轴的姿态曲线
通过以上的试验表明,在保证两个结构相似的六自由度平台的五个特征量 Ra;Rb;da;db;l0等比例相似,且各自的运动轨迹均在其工作空间内时,将采集到的小六自由度平台的各轴运动轨迹之后进行放大,作为六自由度地震模拟试验台的各轴运动轨迹,可以实现相似平台运动轨迹复现。
5 结论
轨迹规划是实现六自由度平台离线编程的关键,本文针对地震模拟试验台的轨迹规划问题,提出了一种离线六自由度平台地震模拟试验台轨迹规划方法,通过对手动六自由度台施加运动,获取手动六自由度平台的6组直线位移传感器的位移数据,依据相似性关系进行比例放大,生成六自由度地震模拟试验台各驱动缸的运动方程,实现对手动六自由度平台的运动过程再现。为六自由度地震模拟试验台控制系统中轨迹规划提供了一定参考价值。
[1]Williams M S,Blakeborough A.Laboratory Testing of Structures under Dynamic Loads:An Introductory Review[J].Philosophical Transactions of the Royal Society A Mathematical Physical&Engineering Sciences,2001,359(1786):1651-1669.
[2]王燕华,程文氵襄,陆 飞,等.地震模拟振动台的发展[J].工程抗震与加固改造,2007,(5):53-56+67.
[3]黄 真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.
[4]张 淼.基于滚珠丝杠传动的六自由度平台设计研究 [J].机械传动,2014,(8):100-103.
[5]Constantinescu D,Croft E A.Smooth and time-optimal trajectory planning for industrial manipulators along specified paths[J].Journal of Robotic Systems,2000,17(5):233-249.
[6]刘 凉,陈超英,赵新华.考虑关节摩擦的并联机器人平滑轨迹规划[J].机械工程学报,2014,(19):9-17.
[7]Khoukhi A,Baron L,Balazinski M.Constrained multi-objective trajectory planning of parallel kinematic machines[J].Robotics and Computer-Integrated Manufacturing,2009,25(4-5):756-769.
[8]贾长志,主编.MD ADAMS虚拟样机从入门到精通[M].北京:机械工业出版社,2010.
[9]Gao Z,Zhang D,Ge Y.Design optimization of a spatial six degree-of-freedom parallel manipulator based on artificial intelligence approaches[J].Robotics and Computer-Integrated Manufacturing,2010,26(2):180-189.
Trajectory planning for 6-DOF earthquake simulation test bench
ZHAI Hua1,2,3,ZHU Xiaofeng1,DING Xu1,3,ZUO Genming4
(1.Institute of Industry and Equipment Technology,Hefei University of Technology,Hefei 230009,Anhui China;2.College of Mechanical and Automotive Engineering,Hefei University of Technology,Hefei 230009,Anhui China;3.Anhui Provincial Key Lab of Aerospace Structural Parts Forming Technology and Equipment,Hefei 230009,Anhui China;4.Anhui New Horizon Science Education&Culture Co.,Ltd.,Tongling 244000,Anhui China)
Taking the 6-DOF(6 degrees of freedom)earthquake simulation test bench as the research object,the position inverse solution model has been constructed.A trajectory planning method of 6-DOF earthquake simulation test bench has been put forward.The similarity relationship between joints space and work space among 6-DOF earthquake simulation test bench and manual 6-DOF platform has been derived through the position inverse solution model.The motion equation of driven cylinder for 6-DOF earthquake simulation test bench has been obtained by use of similarity method.The manual 6-DOF platform motion process has been realized again.The simulation models for 6-DOF earthquake simulation test bench and manual 6-DOF platform have been established.The relationship of motion characteristic curve for driven cylinder and the platform between the 6-DOF platforms with similar structure has been verified according to the simulation and experimental results.It provides reference for the design of control system for 6-DOF earthquake simulation test bench.
6-DOF platform;Trajectory planning;Virtual prototype;Kinematics simulation
TP242.6
A
10.16316/j.issn.1672-0121.2017.04.015
1672-0121(2017)04-0051-05
2017-03-22;
2017-05-10
2016年度安徽省科技计划项目资助(1604a0902129,1604a 0902138)
翟 华(1973-),男,博士,教授,研究院副院长,从事校直工艺理论及设计、液压系统及元件、现代设计理论及方法等研究。E-mail:jxzhaihuajx@sina.com

