DELTA并联机器人极限负载对轨迹控制影响*
谭坚强,王 晗,蔡 念,曾耀斌,李志劲,何国锐,邹学涌
(1.广东工业大学 机电工程学院,广州 510006;2.佛山市质量计量监督检测中心,广东 佛山 528000)
DELTA并联机器人极限负载对轨迹控制影响*
谭坚强1,王 晗1,蔡 念1,曾耀斌2,李志劲2,何国锐2,邹学涌1
(1.广东工业大学 机电工程学院,广州 510006;2.佛山市质量计量监督检测中心,广东 佛山 528000)
为了完成DELTA并联机器人的工作效率最大化、运动稳定性尽可能提高、运动精度和控制精度更加精准等要求,文章针对此要求进行了DELA并联机器人在动平台末端处于极限负载工况的研究。该实验采用编程软件vs2013作为运动控制平台,采用绝对式编码器采集机器人末端位移数据,通过机器人末端轨迹跟踪曲线,得出机器人末端极限负载对DELAT机器人的运动控制精度和轨迹规划产生较大影响的结论。最后文中做出机器人末端极限负载相应的预测趋势图,并做相关实验验证预测趋势图的正确性。
DELTA并联机器人; 极限负载; 极限工况; 轨迹跟踪
0 引言
DELTA并联机器人一般应用于传统的搬运,取放和码垛等任务作业。当DELTA机器人拾取质量较大的工件时,将会对其轨迹跟踪产生较大的影响[1-3]。特别是机器人末端处于极限负载情况下,在工件取放瞬间,将会对机器人的运动控制和轨迹跟踪产生巨大影响,这极有可能影响DELTA并联机器人的控制精度。极限负载是指机器人末端负载质量超过额定负载时,机器人能够处于相对稳定的工作状态。额定负载是指机器人处于稳定工作时,末端所能承受的最大负载质量。当DELTA机器人在极限负载工况下进行码垛作业时,能够极大提高生产效率[4-6]。目前对DELTA机器人的研究基本是在额定负载下进行的。然而,当机器人处于极限负载时,工作的效率最高[9-10]。但实际运用中往往是远远低于极限负载质量,这就造成了伺服电机驱动力的浪费,能量利用率不高。因此针对DELTA并联机器人在取放极限负载质量的工件时,控制精度和运动轨迹将受到较大影响这一极限工况问题,有必要进行深入研究。
目前串联机器人在极限负载情况下有一定研究[4-5], 其主要方法是通过建立虚拟样机模型,利用有限元分析软件进行分析,得出相关应力分布云图,最后验证结构设计合理性或改善结构设计[6-7]。但是这种分析方法不适用与并联机器人,因为并联机器人的运动学和动力学正逆解法跟串联机器人相反,其运动学和动力学的正解建模困难和线性解艰难,反解却相对容易。这导致应用这种串联机器人建模方法,计算量将会极大增加,极大影响DELTA机器人的实时和高速应用要求。
杨瑞鹏等人对并联机器人的负载变化进行过研究[3,8],得出末端变化的负载质量对机器人的运动控制产生较大影响的结论。不过该研究只是在额定负载下的初略分析,对机器人末端处于额定负载和极限负载的情况完全没有涉及。针对这一问题,本研究设计相应的实验系统方案,进行了对机器人末端轨迹跟踪的分析和研究实验。发现了不同极限负载质量工况对DELTA机器人末端轨迹跟踪的规律,针对这规律在实验最后进行了相关实验,验证了本文发现的规律正确性。
1 实验原理与方案
1.1 实验设计原理
设定DELTA并联机器人末端走门字形路径10mm×700mm×10mm,采用直线轨迹插补,梯形速度控制策略,末端负载质量从额定负载质量为3kg,以1kg为步长,逐渐增加到10kg。由于DELTA并联机器人末端吸盘吸力不足,使末端负载容易脱落,所以本系统的负载质量采用沙袋代替,并且用绳子和透明胶固定。位移从空间起始点A(0,-360,-1100)到终点空间点B(0,360,-1100)。通过采集机器人末端位移轨迹和速度等数据,绘制出实际的末端位移曲线和速度曲线,通过跟理论的末端曲线进行对比,评价极限负载对机器人性能的影响。
跟随误差表示运动控制器在理论上驱动机器人关节转角转动一定角度,使机器人末端点在规定时间内到达指定位置,然后该位置跟实际位置的差值就表示跟随误差[7-9]。由于跟随误差可以反映控制器在运动过程中的调节能力,在此选取跟随误差作为DELTA机器人性能优劣的评价指标。本实验方案采用的机器人控制轨迹为门字形路径10mm×700mm×10mm,采用梯形速度控制策略进行实验,满足本实验要求。
1.2 实验系统方案
实验系统包含设备主要有DELTA机器人本体,主控电柜,GUC固高控制,示教屏幕,沙袋,透明胶,电子秤等如图1所示。

图1 3kg负载和DELTA机器人负载实验
其程序的编译环境主要采用vs2013进行编译和控制。其控制流程如图2所示。上位机发出命令控制运动控制器,运动控制器运算后发出指令驱动伺服驱动器,接着伺服电机按照预定指令转动一定角度,机器人末端按预定轨迹进行运动。
1.3 实验系统模型的建立
1.3.1 建立运动学正解模型
对实际的DELTA机器人进行简化,建立模型如图3所示,其中三个平行四边形的中心线B1C1,B2C2,B3C3为引入的虚拟连杆,线段PA1,PA2,PA3分别为直线B1C1,B2C2,B3C3分别沿着直线C1P,C2P,C3P平移得到。
P为动平台中心,O为静平台中心,三个驱动杆的结构角分别为120°。其中静平台半径Rqut=200mm,动平台半径Rmv=45mm,驱动臂长度Ldra=351mm,从动臂长度Lflw=800mm, 主动臂的张角为Ingl。坐标系原点O位于静平台的中心,P为动平台末端质心。
以静平台中心建立世界坐标系[10],由几何关系容易求得Bi(i=1,2,3)点坐标,从而求得Ai(i=1,2,3)三点坐标。
因此运动学正解问题等效于求解三棱锥P-A1A2A3的顶点A坐标问题,其中三棱锥所有边长已知,且三个地面顶点A1A2A3也已经知道。
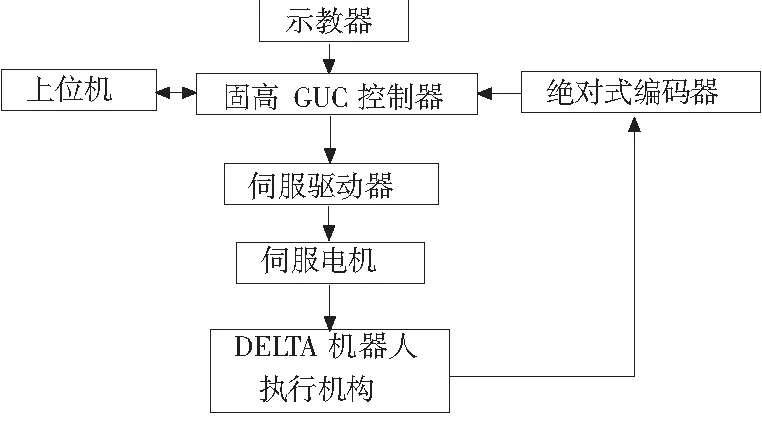
图2 负载实验流程

图3 DELTA机构简图
对于三棱锥P-A1A2A3,过顶点P,做垂线PF垂直于底面A1A2A3,过点F做FG垂直于线段A1A3,由几何关系知道,G为线段BC中点,F为等边三角形A1A2A3外心,如图4所示。
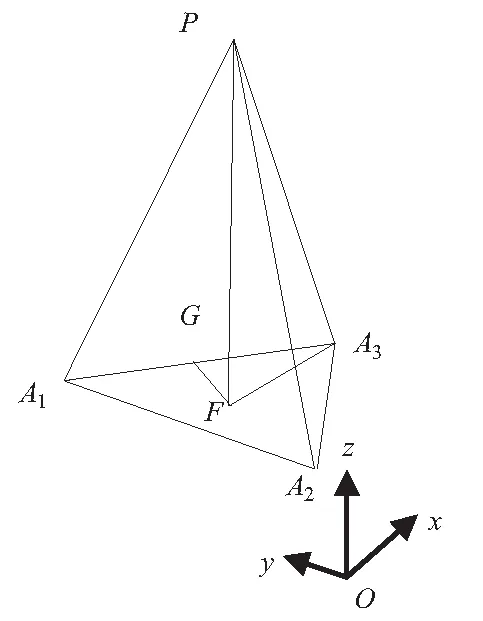
图4 P-A1A2A3三棱锥示意图
利用矢量关系[11],可以求得DELTA机器人的运动学正解如下:
OP=OF+FP
(1)
OF=OG+GF
(2)
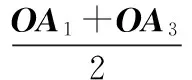
(3)
GF=nGF│GF│
(4)
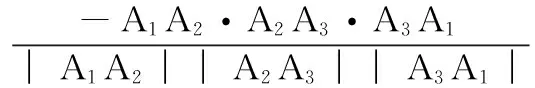
(5)

(6)
FP=nFP│FP│
(7)
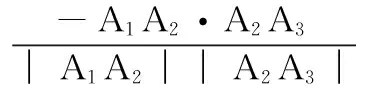
(8)
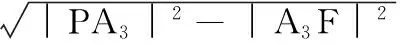
(9)

(10)

(11)
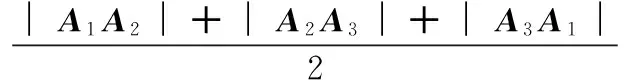
(12)
1.3.2 建立函数控制方程
本文建立的梯形速度控制策略如图5所示[11-15],分别是由加速度运动,恒速运动,减速运动三段曲线组成,设定限制条件当t=0和t=tsum时,机器人末端位移s=0,速度v=0,加速度a=0。根据图5可以求得机器人末端的加速度方程,速度方程和位移方程。
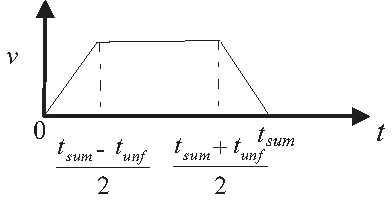
图5 梯形速度控制策略
(13)
(14)
(15)
2 实验结果与分析
DELTA机器人工作的额定负载是3kg,这是机器人能够处于稳定工作的最大负载质量。本研究采用的工作空间为门字形路径,采用梯形速度控制策略,其理论上的末端位移轨迹,速度曲线,加速度曲线分别如图6~图8所示:

图6 理论位移曲线 图7 理论速度曲线
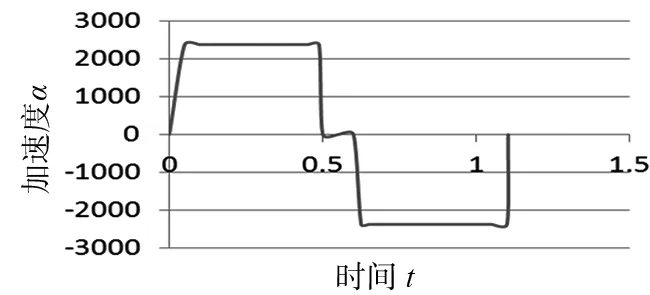
图8 理论加速度曲线
2.1 末端额定负载3kg实验
由于本文的研究主要是分析极限负载质量对机器人末端轨迹跟踪的影响,所以本文选取末端位移跟随误差曲线作为本文的重点研究内容。当末端负载为3kg时,DELTA并联机器人在工作空间走门字形路径,采用梯形速度控制策略,得到的实际和理论上的位移曲线,位移跟随误差曲线如图9和图10所示。
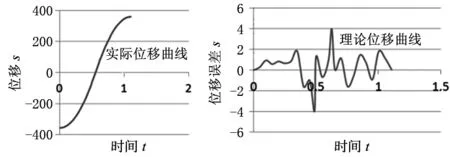
图9 3kg位移曲线 图10 负载3kg位移误差曲线
从图9可以看出理论位移和实验位移除了一些微小误差外基本重合,这表明本实验设计的实验方案是正确合理的。从图10可以看出,跟随误差大致在2mm以内波动,但是却在0.42s和0.68s时出现两个峰值误差4mm。这两个峰值误差将会对机器人的精度控制和末端轨迹跟踪产生较大影响,故有必要对这两个峰值误差进行深入探究。经过查证资料发现这是门字形控制策略导致。当采用梯形速度控制策略时,在机器人末端速度达到最大和开始减速瞬间,加速度从一个常数瞬间减为零,理论上其加加速度无穷大,这将会对机器人末端结构产生了强烈冲击,从而影响了DELTA机器人的控制。
2.2 不同极限负载实验
当末端负载为4kg,6kg,8kg,10kg末端位移和位移误差曲线分别如图11和图12所示。

图11 4kg~10kg位移 图12 4kg~10kg位移误差
由图13可知,DELTA并联机器人末端轨迹控制跟其末端极限负载有关,末端极限负载越大,其轨迹跟踪误差越大。
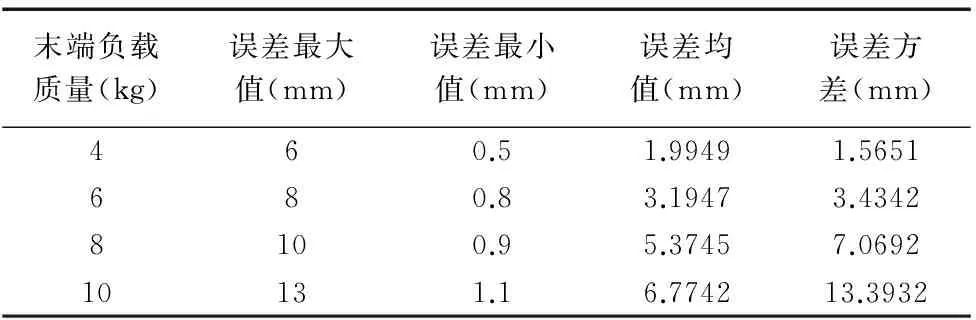
表1 极限负载实际误差
由表1可知,机器人末端极限负载质量严重影响末端的轨迹跟踪和运动控制精度。当机器人末端极限负载质量越大时,其末端轨迹跟踪的最大误差和最小值误差也相应增加。其末端均值误差和方差也跟随者增加说明了机器人的稳定性随着末端极限负载质量的增加而越来越差。
对此,根据上面表格中的实验数据,拟合出一条大致的极限误差-负载趋势图如图13所示。同理,拟合出末端位移误差方差-负载趋势图如图14所示。
由图13可知机器人末端负载越大,其误差均值越大,且呈现正相关趋势。通过图14可以得知,末端极限负载越大,位移误差方差呈现指数增长。可以根据这个末端位移误差均值与负载趋势图和末端位移误差方差与负载趋势图,本研究分别进行了末端极限负载为5kg,7kg,9kg实验,以验证图13和图14的正确性。其结果如图15,图16和表格2所示。

图13 均值预测 图14 方差预测
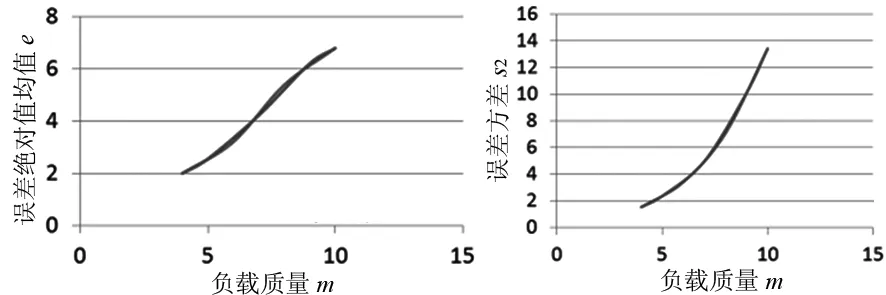
图15 均值预测 图16 方差预测
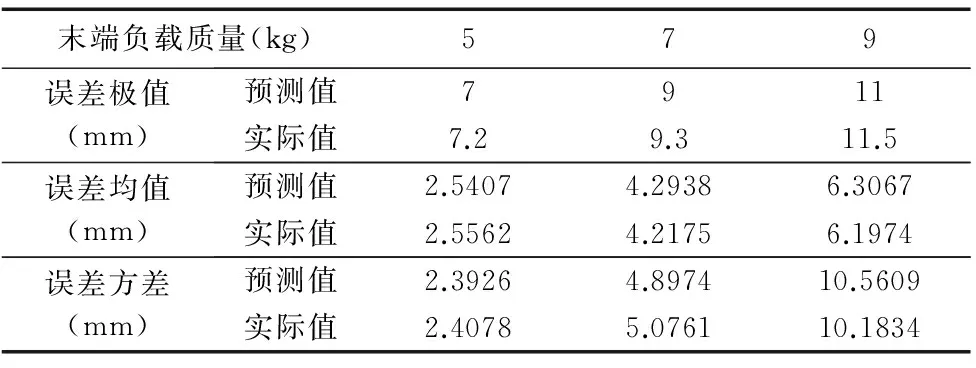
末端负载质量(kg)579误差极值(mm)预测值7911实际值7.29.311.5误差均值(mm)预测值2.54074.29386.3067实际值2.55624.21756.1974误差方差(mm)预测值2.39264.897410.5609实际值2.40785.076110.1834
由图15和图16以及表2可知,预测值与实际值大致相吻合,误差不超过0.5mm,说明本文做出的预测图13和图14是正确和合理的。
3 结论
研究主要对DELTA并联机器人处于极限负载这一极限工况进行了详细的分析,发现了极限负载质量跟DELTA机器人末端轨迹跟踪误差绝对值均值成一次函数关系,跟末端轨迹跟踪误差方差呈现指数函数关系这一规律。这一规律可以对机器人运动控制编程人员进行误差补偿时提供参考。
研究提出了一种新思路,选取跟随误差作为轨迹跟踪好坏的评价标准,通过改变末端极限负载质量,进行相关研究。这对后续学者想研究极限负载质量工况对机器人轨迹跟踪的影响具有相当大的参考价值,同时这也为后期研究极限负载质量工况对DELTA机器人关节空间的控制影响这一课题具有非常大的参考意义。
[1] 刘善增,余跃庆,杜兆才. 并联机器人的研究进展与现状[J]. 组合机床与自动化加工技术,2007(7):4-10.
[2] Islam S Liu P X. Adaptive Output Feedback Control of Robot Manipulators Using High-gain Observer[C]//2009 22th International Conference on Intelligent Robots and Systems. IEEE/RSJ, 2009:868-885.
[3] 杨瑞鹏. 面向负载大范围变化的取放操作并联机器人运动控制研究[D].哈尔滨:哈尔滨工业大学,2012
[4] Qiang Y, Jing F, Zeng J, et al. Dynamic modeling and vibration mode analysis for an industrial robot with rigid links and flexible joints[C]// Control and Decision Conference (CCDC), 2012 24th Chinese. IEEE, 2012: 3317-3321.
[5] 赵欣翔.考虑关节柔性的重载工业机器人结构优化研究[D].哈尔滨:哈尔滨工业大学,2013.
[6] 孙兴伟,董蔚,王可. 数控机床伺服系统跟随误差对加工轮廓的影响[J]. 制造技术与机床, 2010 (6) : 76-78.
[7] S Q Li, Y Y Zou, Y J Li S,et al. Kinematic Performance Evaluation for heavy duty Industrial Robot[C]// 2014 4th International Conference on Machinery, Materials Science and Engineering Applications (MMSE). EI, 2014:148-152.
[8] 李树强.重载搬运机器人运动/载荷性能测试与评估[D].沈阳:沈阳理工大学,2015.
[9] Paccot F, Lemoine P, Andreff A N, et al. Vision-based Computed Torque Control for Parallel Kinematic Machines[C]//2008 13th International Conference on Robotics and Automation,IEEE, 2008:1556-1561.
[10] P Dzitac,A M Mazid. An Efficient Control Configuration Development for a High-speed Robotic Palletizing System[C]//2008 7th International Conference on Robotics, Automation and Mechatronics (CAM),2008:140-145.
[11] D Meike, L Ribickis. Energy efficient use of robotics in the automobile industry[C]//2011 15th International Conference on Advanced Robotics [CA]. IEEE, 2011: 507-511.
[12] 丛明,熊永康,刘冬.一种并联机器人操作空间最优时间轨迹规划方法机械设计[J]. 机械设计,2016(2):7-13.
[13] R J Moreno Masey, J O Gray. Elliptical Point to Point Trajectory Planning using Electronic CamMotion Profiles for High Speed Industrial Pick and Place Robots [C]//2009 14th International Conference on Emerging Technology & Factory Automation (ETFA). IEEE, 2009:168-174.
[14] X Yang, Z Feng, C Liu,X Ren.A geometric method for kinematics of delta robot and its path tracking control[C]// 2014 14th International Conference on Control and Automation (CA). IEEE, 2014:509-514.
[15] 孙兴伟,董蔚,王可. 数控机床伺服系统跟随误差对加工轮廓的影响[J]. 制造技术与机床, 2010(6):76-78.
AnalysisandResearchonLimitingConditionofDELTAParallelManipulator
TAN Jian-qiang1, WANG Han1,CAI Nian1,ZENG Yao-bin2,LI Zhi-jin2,HE Guo-rui2,ZOU Xue-yong1
(1.School of Electromechanical Engineering, Guangdong University of Technology, Guangzhou 510006,China; 2.Foshan Quality Measurement Supervision and Inspection Center, Foshan Guangdong 528000,China)
In order to improve the working efficiency, the motion stability, the moving precision and control precision of DELTA parallel manipulator, this paper completes the analysis of limiting load of DELA parallel manipulator. In this study, the programming software of vs2013 was used as the motion control platform. Absolute encoders were used to collect the displacement data of the robot terminal. By comparing the trajectory tracking with the theoretical displacement curve, my research deserve a conclusion that Limit load for DELAT robot at the end of the robot motion control accuracy and trajectory planning have great influence. for verifying the correctness of the forecasting trend , this paper, Finally, makes the prediction trend of the ultimate load of the robot.
DELTA parallel manipulator; limit load; limit condition; trajectory tracking
TH165;TG659
A
1001-2265(2017)12-0062-04
10.13462/j.cnki.mmtamt.2017.12.015
2017-02-15;
2017-03-09
广东省前沿与关键技术创新专项资金(2015B010124001);东莞市产学研项目(2013509109101);广东省科技计划项目:协同创新与平台环境建设(2015B010102014);“广东特支计划”科技青年拔尖人才项目(2014TQ01X212);广东省高等学校优秀青年教师培养计划(YQ2015056);广东省自然科学基金(2015A030312008);广生省公益研究项目(2015B010104006)
谭坚强(1991—),男,广东韶关人,广东工业大学硕士研究生,研究方向为工业机器人,(E-mail)270307920@qq.com;通讯作者:王晗(1980—),男,广州人,广东工业大学教授,硕士生导师,博士,研究方向为微纳加工与精密测量,(E-mail)wanghangood@gdut.edu.cn。
(编辑李秀敏)

