高压氧疗法应用于慢性伤口问题解的存在唯一性

邵少霞，冯兆永，卫雪梅

(1. 广东工业大学应用数学学院，广东 广州 510520；2. 中山大学数学学院，广东 广州 510275)

高压氧疗法应用于慢性伤口问题解的存在唯一性

邵少霞1，冯兆永2，卫雪梅1

(1. 广东工业大学应用数学学院，广东 广州 510520；2. 中山大学数学学院，广东 广州 510275)

研究一个高压氧治疗对慢性伤口愈合问题的数学模型。该模型包含了描述氧扩散浓度的非线性二阶抛物型方程、关于毛细管尖端密度的非线性一阶双曲型方程以及一个描述血管密度的常微分方程。通过应用双曲方程的特征理论、Lp估计、Hölder估计以及Banach不动点定理证明了这个问题整体解的存在唯一性。

高压氧治疗；慢性伤口；局部解；整体解；存在唯一性

许多生物生长的基本规律都可以用偏微分方程的数学模型来表示[1-14]。近年来，据统计中国目前的糖尿病患者大约2.4亿，随之而来的糖尿病相关慢性难愈性伤口，尤其是糖尿病足的发生率显著上升，更为严重的是15% 的糖尿病足患者最终只能接受截肢治疗，因此对如何治疗慢性伤口具有非常深远的研究意义。慢性伤口的愈合是一个极其复杂的过程，而局部缺血是伤口难愈合过程中的一个重要因素。Friedman等[3-6]建立了关于局部皮肤缺血性慢性伤口的数学模型，并研究了在自由边界条件下其解的存在性和唯一性。此后，随着科学的发展，一系列关于血管生成的慢性伤口愈合模型被Pettet等[7-10]提出，这些学者根据各自的生物实验和临床数据模拟慢性伤口愈合的过程，从而从实验角度上说明已建立模型的合理性。在之前工作的基础上，Flegg等[11-14]提出了用高压氧疗法来治疗慢性伤口，通过模拟高压氧疗法在慢性伤口愈合中的作用，预测间歇性高压氧疗法将有助于慢性伤口的愈合，而正常氧气在治疗这样的慢性伤口时没有明显的效果。此外，那些动脉供血充足的患者对高压氧疗法具有良好的伤口愈合反应。本文将研究由Flegg等[14]在2012年提出的一个高压氧疗法应用于慢性伤口的数学模型，具体模型如下：

0≤x≤L，t>0

(1)

(2)

w(x,0)=w0(x)，0≤x≤L

(3)

k5bH(w-wL)H(wH-w)，

0≤x≤L，t>0

(4)

n(x,0)=0，0≤x≤L

(5)

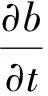
(6)

b(x,0)=b0(x)，0≤x≤L

(7)

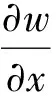
和

k2、k4、k5、k6、χ、wL、wH、Dw均为正常数(具体含义详见文献[14])。

显然w0(x)≥0且有界，w0(x)∈C2+α([0，L])，H(u)为有界连续函数，记H(u)∞≤M，而b0(x)≥0且有界，b0(x)∈C1([0，L])。

本文的主要结论如下：

定理1 对∀t≥0，问题(1)-(7)存在唯一的整体解。

1 预备引理

下面我们将介绍一些引理，首先引入一些记号。

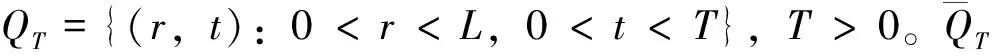
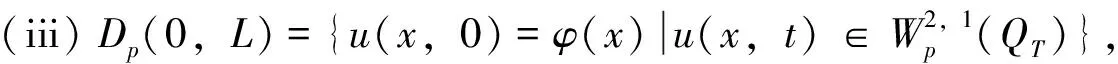
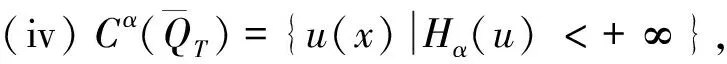
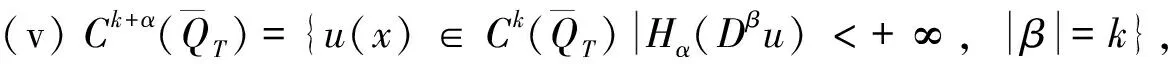
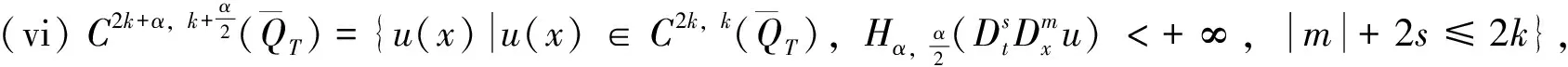
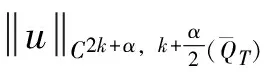
其中

下面介绍几个本文研究过程中所用到的引理。

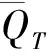
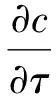
0≤z≤1， 0≤t≤T

(8)

z=0，1：Bc=φ， 0≤τ≤T

(9)

c(z，0)=c0(z)， 0≤z≤1

(10)

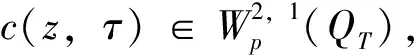
(11)

引理2[16]假设D是一个正常数

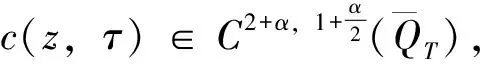
当(2)α=1，β≥0时，成立

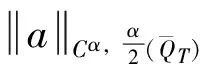
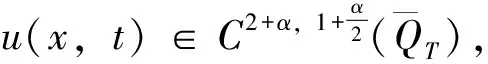
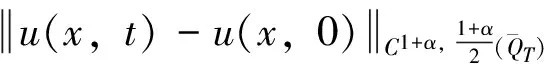
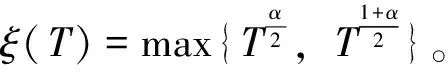
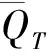
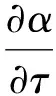
0≤ρ≤L， 0≤τ≤T

(12)

α(ρ，0)=α0(ρ)， 0≤ρ≤L

(13)

(14)

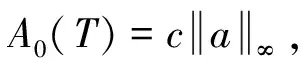
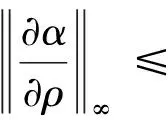
(15)

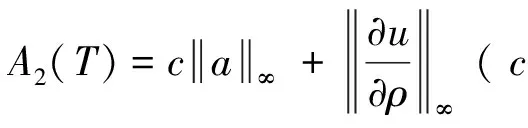
进一步，若对任意的0≤ρ≤L，0≤τ≤T，若增加

α0≥0，f(ρ，τ)≥0

(16)

则有

α(ρ，τ)≥0， 0≤ρ≤L， 0≤τ≤T

(17)

证明类似于文献[18]。

2 局部解的存在唯一性

将运用Banach不动点定理证明问题(1)-(7)存在局部唯一解。对于给定的T和正整数M，引进度量空间(XT，d)：XT是由所有的向量函数(w(x，t)，n(x，t)，b(x，t))(0≤x≤L，0≤t≤T)组成，且它们满足如下条件

(i)

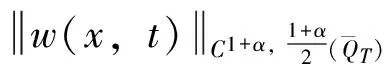
对任意的0≤x≤L， 0≤t≤T；

(ii)

对任意的0≤x≤L， 0≤t≤T；

(iii)

对任意的0≤x≤L， 0≤t≤T。

定义XT中的度量空间d为

d((w1，n1，b1)，(w2，n2，b2))=

易知度量空间(XT，d)是一个完备的度量空间。

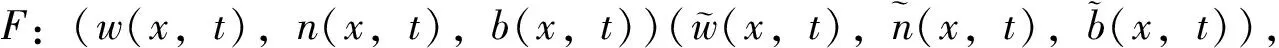
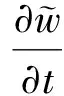
(18)

(19)

(20)

k5bH(w-wL)H(wH-w)， 0≤x≤L，t>0

(21)

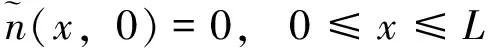
(22)

(23)

(24)

首先证F映XT到XT自身。

结合引理3可得

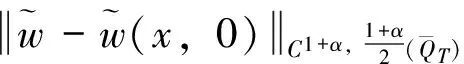
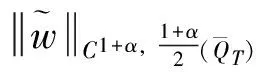
(25)

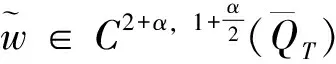
且满足

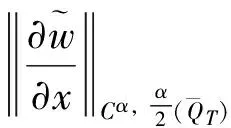
(26)

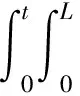
其中

G(x，ξ，t)=

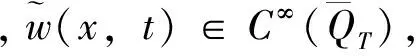
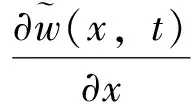
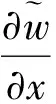
(27)

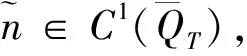
(28)

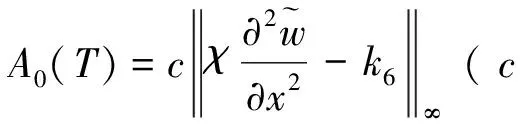
(29)

(Ⅲ) 考虑问题(23)-(24)，直接计算可得

0≤t≤T

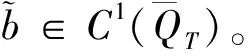
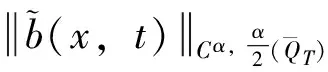
(30)

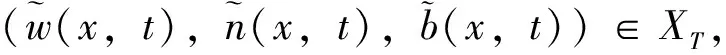
接下来证F是压缩映射。

0≤x≤L，0≤t≤T

(31)

(32)

(33)

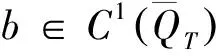
(34)

(35)

其中

G(x，ξ，t)=

则

(36)

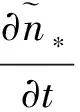
0≤x≤L， 0≤t≤T

(37)

(38)

其中

F1(x，t)=k5(b1H1(w-wL)H1(wH-w)-

b2H2(w-wL)H2(wH-w))+

由(28)式和(29)式可推出

(39)

(40)

(41)

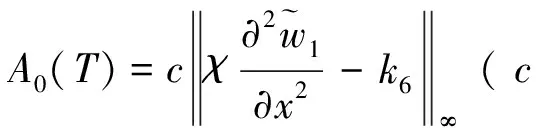
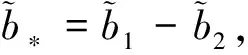
0≤x≤L， 0≤t≤T

(42)

(43)

其中

直接计算可得

(44)

(45)

所以，结合(35)、(41)和(45)式有

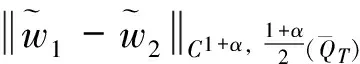
因此，取T充分小使得C(T)M≤1时，F为压缩映射。根据Banach不动点定理， 定义在映射F上的一个固定点(w(x，t)，n(x，t)，b(x，t))∈XT，使得对任意的0≤t≤T，问题(1)-(7)有唯一古典解(w(x，t)，n(x，t)，b(x，t))，注意到T依赖于w0(x)在C2+α([0，L])空间和b0(x)在C1([0，L])空间上范数的上确界。

由上述证明可总结为如下定理：

定理2 存在T>0，使得所有t∈[0，T]，问题(1)-(7)存在唯一解，其中T依赖于w0(x)在C2+α([0，L])空间和b0(x)在C1([0，L])空间上范数的上确界。

3 整体解的存在唯一性

引理5 问题(1)-(7)的解有如下结论

w(x，t)≥0，n(x，t)≥0，b(x，t)≥0

证明现在考虑方程组 (1)-(7)。

(i) 当b(x，t)≥0时，根据上下解原理可知w(x，t)≥0，结合(17)式可推得n(x，t)≥0。

事实上，当b(x，t)≥0时，若w(x，t)<0或n(x，t)<0之一成立，由上下解原理易知w(x，t)<0，n(x，t)≥0；w(x，t)≥0，n(x，t)<0和w(x，t)<0，n(x，t)<0的情况不成立。

(ii) 当b(x，t)<0时，若w(x，t)≥0或n(x，t)≥0之一成立，由上下解原理易推出w(x，t)<0，n(x，t)≥0；w(x，t)≥0，n(x，t)<0和w(x，t)≥0，n(x，t)≥0的情况不成立。

当b(x，t)<0，w(x，t)<0，n(x，t)<0时，显然问题(1)-(3)的解为

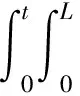
其中

G(x，ξ，t)=

由以上结果可推出

而

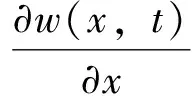
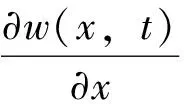
结合(i),(ii)可知w(x，t)≥0，n(x，t)≥0，b(x，t)≥0。引理5得证。

引理6 存在依赖于时间T的常数C(T)，满足

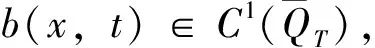
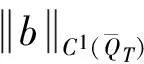
(46)

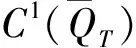
(47)

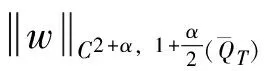
(48)

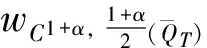
(50)

综上所述，由(48)、(49)和(50)式可知，引理6得证。

根据定理2、引理5和引理6 以及时间T的任意性可证得本文的主要结论定理1。

[1] 丛百利，冯兆永，卫雪梅. 一个免疫细胞抑制肿瘤免疫逃逸模型整体解的存在唯一性[J]. 中山大学学报(自然科学版)，2015, 54(3): 36-43.

CONG B L,FENG Z Y,WEI X M. Existence and uniqueness of global solution for a model of immune cells inhibiting tumor immune evasion [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2015, 54(3): 36-43.

[2] 高帅帅，卫雪梅，冯兆永. 一个肿瘤化学治疗空间结构模型的定性分析[J]. 中山大学学报(自然科学版)，2012, 51(2): 30-34.

GAO S S, WEI X M, FENG Z Y. Analysis of a mathematical model of the response of spatially structured tumors to chemotherapy model [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2012, 51(2): 30-34.

[3] FRIEDMAN A, HU B, XUE C. Analysis of a mathematical model of ischemic cutaneous wounds [J]. SIAM Journal on Mathematical Analysis, 2010, 42(5): 2013-2040.

[4] FRIEDMAN A, XUE C. A mathematical model for chronic wounds [J]. Mathematical Biosciences and Engineering: Mbe, 2011, 8(2): 253-261.

[5] FRIEDMAN A, HU B, XUE C. A three dimensional model of wound healing: analysis and computation [J]. Discrete and Continuous Dynamical Systems-Series B (DCDS-B), 2012, 17(8): 2691-2712.

[6] XUE C, FRIEDMAN A, SEN C K. A mathematical model of ischemic cutaneous wounds [J]. Proceedings of the National Academy of Sciences of USA, 2009, 106(39): 16782-16787.

[7] PETTET G, CHAPLAIN M A J, MCELWAIN D L S, et al. On the role of angiogenesis in wound healing [J]. Royal Society Proceedings B: Biological Sciences, 1996, 263(1376): 1487-1493.

[8] OLSEN L, SHERRATT J A, MAINI P K, et al. A mathematical model for the capillary endothelial cell-extracellular matrix interactions in wound-healing angiogenesis [J]. Mathematics Applied in Medicine and Biology, 1997, 14(4): 261-281.

[9] PETTET G J, BYRNE H M, MCELWAIN D L S, et al. A model of wound-healing angiogenesis in soft tissue [J]. Mathematical Biosciences, 1996, 136(1): 35-63.

[10] SCHUGART R C, FRIEDMAN A, ZHAO R, et al. Wound angiogenesis as a function of tissue oxygen tension: A mathematical model [J]. Proceedings of the National Academy of Sciences of USA, 2008, 105(7): 2628-2633.

[11] FLEGG J A, MCELWAIN D L S, BYRNE H M, et al. A three species model to simulate application of hyperbaric oxygen therapy to chronic wounds [J]. Plos Comput Biol, 2009, 5(7): 1-12.

[12] FLEGG J A, BYRNE H M, MCELWAIN D L S. Mathematical model of hyperbaric oxygen therapy applied to chronic diabetic wounds [J]. Bulletin of Mathematical Biology, 2010, 72(7): 1867-1891.

[13] FLEGG J A. Mathematical modelling of chronic wound healing [D]. Queensland University of Technology, 2009.

[14] FLEGG J A, BYRNE H M, FLEGG M B, et al. Wound healing angiogenesis: the clinical implications of a simple mathematical model [J]. Journal of Theoretical Biology, 2012, 300(5): 309-316.

[15] LADYZENSKAJA O A, SOLONNIKOV V A, URALTSEVA N N. Linear and quasilinear partial differential equations of parabolic type translations of mathematical monographs [M]. Amer Math Soc, 1968, 23.

[16] FRIEDMAN A, LOLAS G. Analysis of a mathematical model of tumor lymphangiogenesis [J]. Mathematical Models and Methods in Applied Sciences, 2005, 15(1): 95-107.

[17] WEI X, CUI S. Existence and uniqueness of global solutions for a mathematical model of antiangiogenesis in tumor growth [J]. Nonlinear Analysis: Real World Applications, 2008, 9(5): 1827-1836.

[18] CUI S B, WEI X M. Global Existence for a parabolic-hyperbolic free boundary problem modelling tumor growth[J]. Acta Mathematicae Applicatae Sinica, 2005, 21(4): 597-614.

[19] 姜礼尚，陈亚浙. 数学物理方程讲义[M]. 北京: 高等教育出版社，1986: 150-157.

Existenceofglobalsolutionforchronicwoundbyhyperbaricoxygentherapy

SHAOShaoxia1,FENGZhaoyong2,WEIXuemei1

(1.School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China;2. School of Mathematics, Sun Yat-sen University, Guangzhou 510275, China)

A mathematical model of hyperbaric oxygen therapy for chronic wound healing is studied. This model contains a nonlinear second-order parabolic equation describing the concentration of oxygen diffusion，a nonlinear first-order hyperbolic equation for capillary tip density and an ordinary differential equation for blood vessel density. The existence and uniqueness of the global solution is proved by applying the characteristic theory of hyperbolic equation, theLp-theory，Hölder-estimate theory and Banach fixed point theorem.

hyperbaric oxygen therapy; chronic wound; local solution; global solution; existence and uniqueness

10.13471/j.cnki.acta.snus.2017.06.006

2017-03-13

国家自然科学基金(11101095, 11471339)；广东省高校特色创新类项目(2016KTSCX028)；广东省高层次人才项目(2014011)；研究生教育创新项目(2014QTLXXM17)

邵少霞(1992年生)， 女；研究方向偏微分方程；E-mail：2271567652@qq.com

卫雪梅(1972年生)，女；研究方向偏微分方程；E-mail：wxm_gdut@163.com

O175

A

0529-6579(2017)06-0048-07