黄土平面蠕变模型

郭鸿，骆亚生，胡连信，王鹏程

(1.陕西理工大学，陕西 汉中 723000；2. 西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100；3.法国国立应用科学学院，法国 里昂 69100；4.中建市政工程有限公司，北京 100071)

黄土平面蠕变模型

郭鸿1，骆亚生2，胡连信3，王鹏程4

(1.陕西理工大学，陕西 汉中 723000；2. 西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100；3.法国国立应用科学学院，法国 里昂 69100；4.中建市政工程有限公司，北京 100071)

在岩土工程中，有许多问题可归纳为平面应变问题，对其长期稳定性的研究采用平面蠕变试验更符合实际情况。采用改造的平面蠕变仪进行了一系列室内固结蠕变试验，发现：在大剪应力、高含水率以及低固结压力条件下黄土平面蠕变量较大；基于试验数据分析，建立了一种适合于黄土平面蠕变的模型公式。与Singh-Mitchell和Mesri模型的对比表明：该模型具有精度高、参数少且易获得等优点，能较好地模拟黄土平面应变状态下的蠕变特性。

黄土；平面蠕变；蠕变模型

黄土在世界范围内广泛分布。因一般黄土地区的地下水埋藏较深，黄土多处于非饱和状态。非饱和黄土具有典型的大孔隙、质地疏松、高含量可溶盐、湿陷性等特点[1]。随着含水率的增加，或者一些人为因素的影响导致黄土周围压力降低，会使得黄土结构的强度、稳定性出现下降。如果建筑物在黄土地区发生蠕变，无疑将会带来沉降等工程隐患。因此，全面地了解黄土蠕变的影响因素和规律对预防、治理黄土地区建筑构的工后沉降及变形有重要的实践意义。

许多工程结构在长度方向的断面形状不变，其应力状态可视为平面应变状态。针对这类平面应变状态的长期沉降问题，本文采用平面蠕变试验来代替常规三轴蠕变试验，来分析实际土体的蠕变变化规律。国内外学者关于常规三轴蠕变试验[2-10]的研究较多。近年来，逐渐兴起了多轴蠕变试验和离散元数值模拟法[11-13]。然而，黄土的平面蠕变方面却少有人涉及。同时，黄土地区因平面蠕变产生的工程问题却屡见不鲜，如：黄土河堤和黄土路基的蠕变破坏等。因此，本文利用改进的平面蠕变仪对黄土做了一系列平面蠕变试验，探究了不同含水率、固结压力下重塑黄土的蠕变特性；基于室内试验结果，建立了黄土平面蠕变模型，并与已有的Singh-Mitchell和Mesri模型[14-16]进行了对比，以期为工程实践提供理论支撑。

1 试验材料和方法

试验所取土样来自陕西省泾阳县某砖厂，为Q3黄土。黄土取土深度为3.0～4.0 m，天然含水率为16.2%，天然干密度为1.28 g/cm3，孔隙比为1.14，其基本的物理力学指标如表1所示。

表1 基本物理力学指标Table 1 Basic physical and mechanical properties

[17]的思路，在2个柔性加压作用面(88.9 mm×88.9 mm)处加侧限约束使其成为零应变面，将日本谷藤机械工业株式会社生产的TS-525式真三轴仪改造为平面蠕变仪。两侧小侧面(88.9 mm×35.56 mm)由侧板上的气压加压(空压机提供气压)，并将这个面定为中主应力面(σ3方向)。轴向荷载通过支架由砝码提供，并将这个面定为大主应力面(σ1方向)。其中，两小侧面装有自动变形采集系统，轴向变形采用量程30 mm，精度0.01 mm的百分表测量。改造所用材料的强度与尺寸均符合实验要求，所有加压砝码和百分表均通过国家计量认证。后期试验表明改造的压力室能较好适用平面应变的相关试验[17]。试样尺寸如图1所示。需要指出的是，本文所研究的内容为平面蠕变条件，和三轴蠕变的区别是不需要考虑a面的应变。

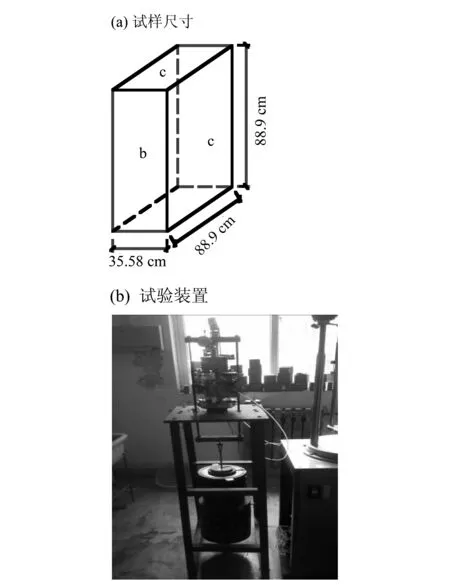
图1 试样尺寸、压力室及试验装置Fig.1 Samples dimension and test device

试样为非饱和重塑黄土样，由所取地区黄土风干、碾碎、过筛后压实制作而成。采用水膜转移法控制试样含水率在10%、20%、30%，并置于保湿缸内静置48 h以上，保证试样水分均匀分布。控制干密度为1.53 g/cm3(压实度为90%)。试验分3个固结压力(50、100、150 kPa)和6级剪应力(50、100、150、200、250、300 kPa)，剪应力采用分级加载方式。试验开始时，先将试样在σ1=σ3的条件下固结，待固结完全稳定后开始施加第一级轴向剪应力(σ1﹣σ3)荷载。每级加载后待试样变形稳定再加下一级荷载，固结及轴变稳定以变形小于0.01 mm/4 h为标准。整个试验过程中，保证σ2方向形变为零。因本试验手段处于探索阶段，故最大剪应力采用类似三轴蠕变的定义方法，即其他剪应力值由最大剪应力与加载级数的比值而定。加载过程中允许试样排水排气，当试样轴向形变大于15%，或出现急剧变形可视为试样压缩蠕变破坏。

2 试验结果分析

2.1 蠕变试验结果分析

蠕变试验数据处理采用Boltzmann叠加原理，结果如图2～4所示。

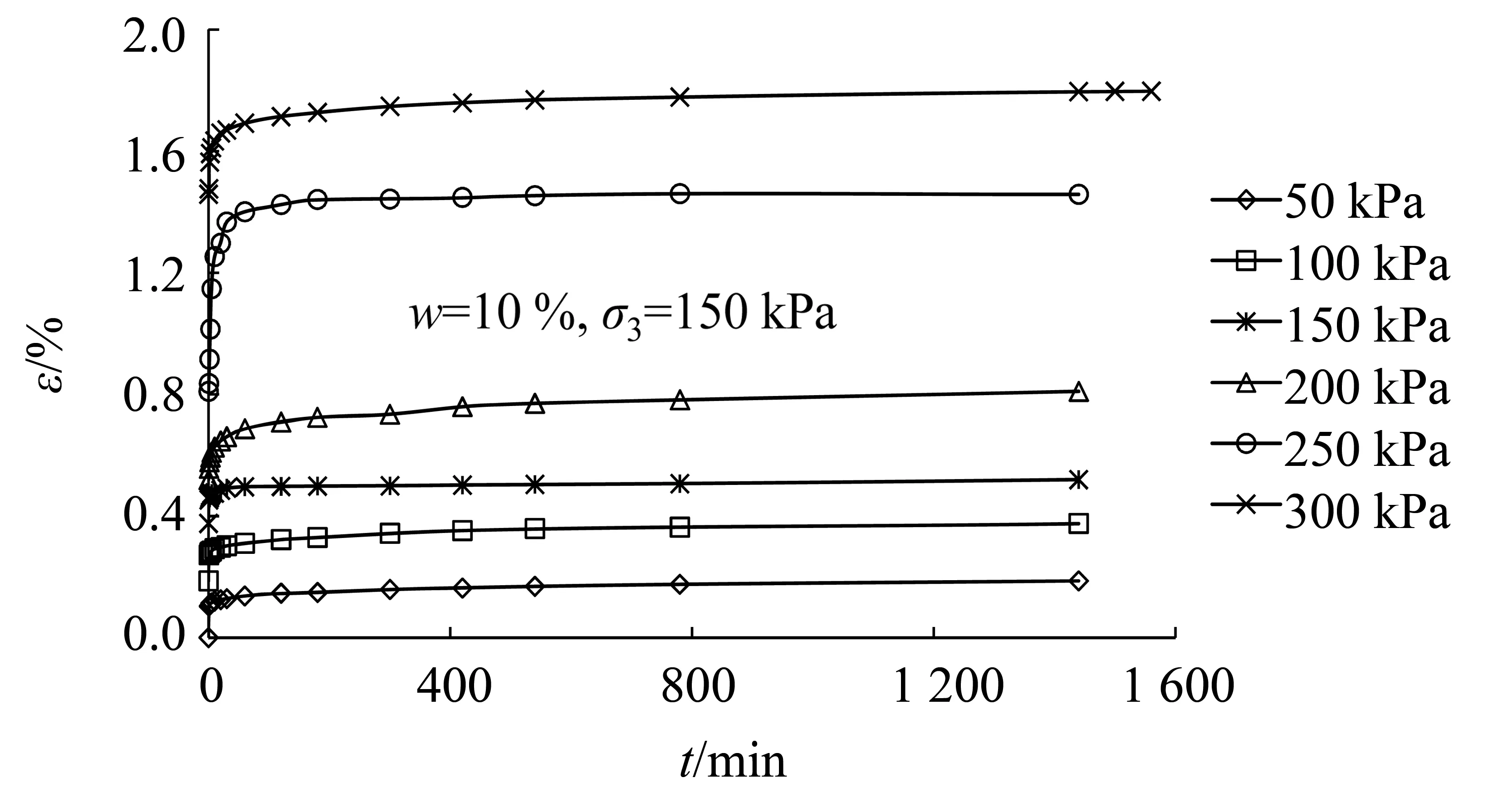
图2 各级剪应力下的蠕变曲线Fig.2 Creep curves under different deviaoric stresses

以含水率w=10%、固结压力σ3=150 kPa的试验为例，分析可知：试样经过短暂的瞬时变形后进入衰减蠕变变形阶段，然后达到等速蠕变变形阶段。当剪应力相对较低时，重塑土样内部结构调整较为迅速，变形在短时间内趋于稳定，蠕变现象不明显。当剪应力较大时，土体内部结构调整所需时间延长，蠕变现象明显，表现为等速蠕变现象，土样达到蠕变稳定所需时间变长。

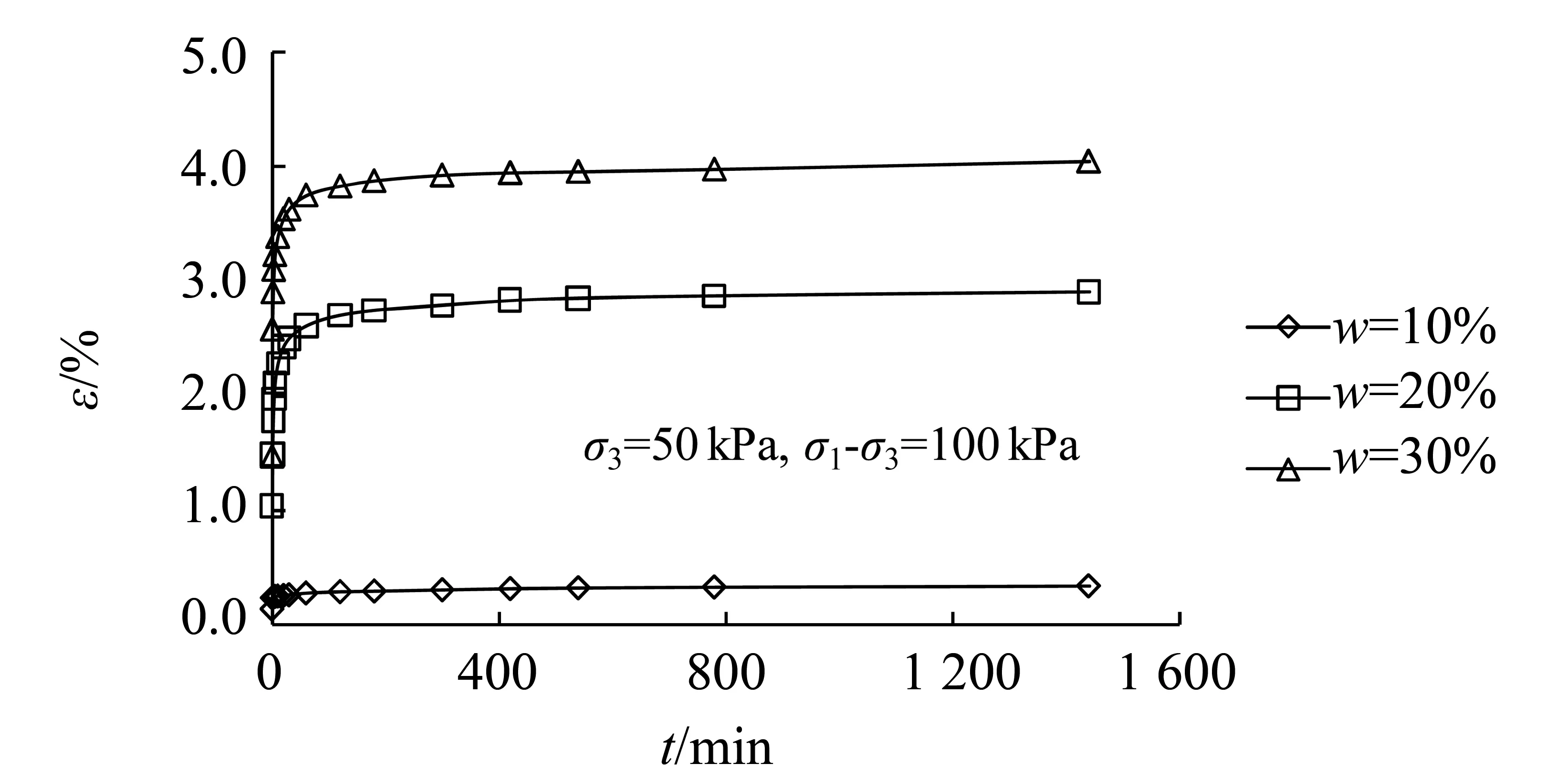
图3 不同含水率下的应变-时间曲线Fig.3 Stress-strain curves under different water contents

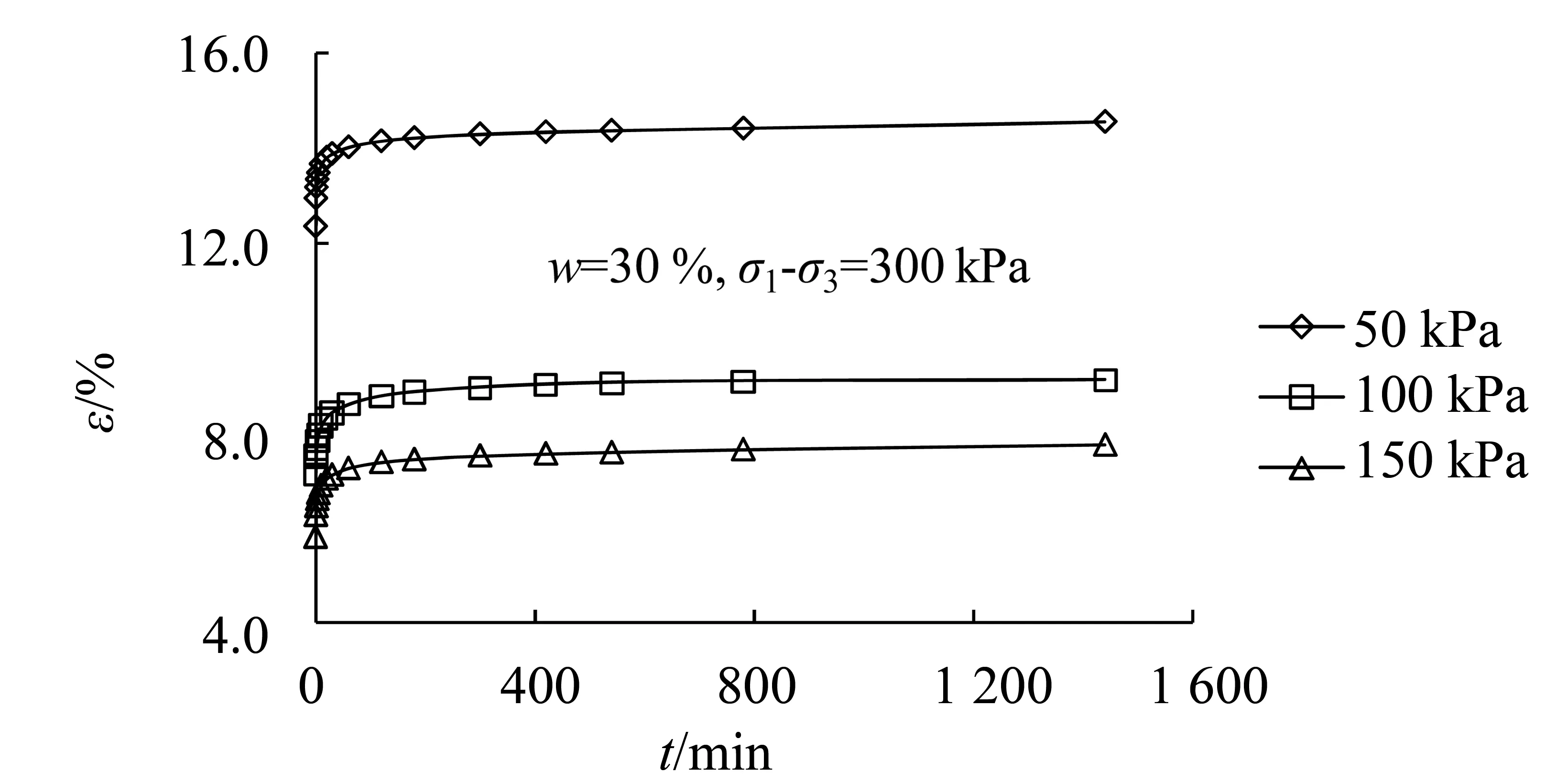
图4 不同固结压力下的应变-时间曲线Fig.4 Stress-strain curves under different confining pressure

含水率和固结压力对平面蠕变影响显著，表现为当其他条件一定时，含水率愈大，蠕变现象愈明显，形变愈大；固结压力愈大，蠕变形变愈小。在实际工程中，可通过改善边坡排水降低土体内部含水率，增加上覆荷载、延长加荷时间提高土体固结度等方法来减小工后蠕变沉降，降低蠕变破坏的可能。

2.2 经验模型建立

2.2.1 模型的提出 利用各含水率、固结压力下的平面蠕变试验结果，建立平面蠕变模型。通过对蠕变应变-时间的拟合，得到蠕变形变与剪应力、经历时间的表达式为：

(1)

(2)

其中：σ1-σ3为剪应力，(σ1-σ3)f为实际破坏应力差。在本次试验中，采取类似三轴压缩求解剪应力的方法[14]，并结合黏聚力c、内摩擦角φ、σ3值可求得(σ1-σ3)f值，再利用式(2)计算各个剪应力下的剪应力水平值。

2.2.2 模型参数的确定 对于拟合参数的确定，可以通过计算机编程拟合的方法实现。但拟合所得到的参数往往不利于实际工程的推广应用。本文采用王松鹤和骆亚生[9]的复杂应力下蠕变模型参数的确定方法，分别取t=0和t=∞时刻的蠕变量，求得模型参数a、b、n。

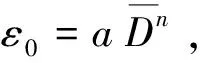
(3)

图关系曲线Fig.5 Relation curves between Lnε0 and ln

2.2.3 模型验证 用式(3)对w=20%、σ3=50 kPa下的6组剪应力蠕变曲线进行拟合，结果如图6所示。

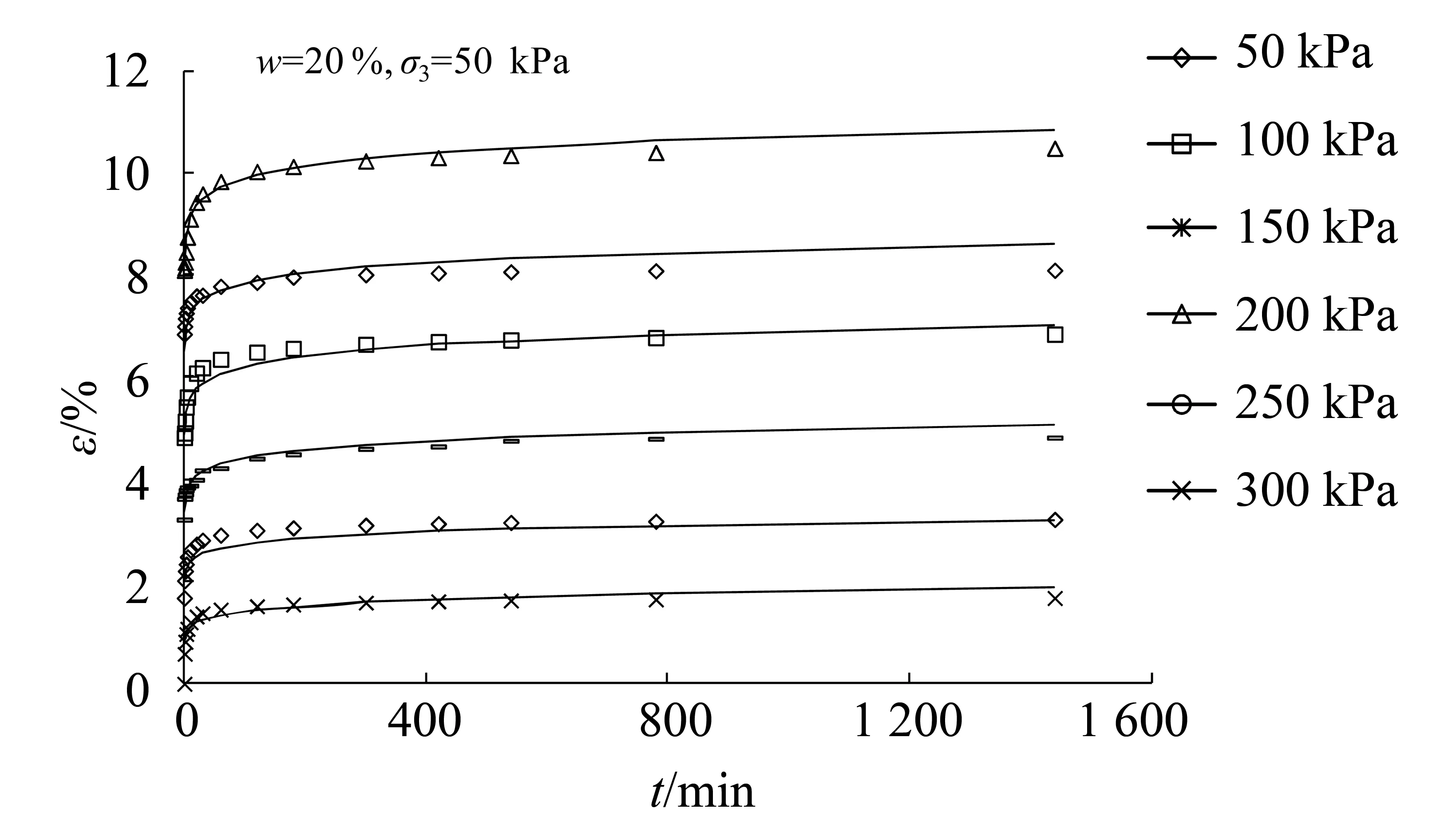
图6 模型验证Fig.6 Model validation

从图中可以看出，当剪应力较小时，模型公式对实际蠕变过程的拟合比较合理，两者趋势相同；当剪应力较大时，模型公式对实际蠕变过程拟合稍有偏差，表现为公式模拟值在实际试验值附近跳动。同时，模型其他剪应力条件下的蠕变拟合结果精度较高，说明该模型公式在描述实际黄土平面蠕变的应力应变-时间关系时效果良好。

2.3 不同蠕变模型的比较

土体蠕变模型有很多，比较常见的是Singh-Mitchell模型和Mesri模型。Singh-Mitchell模型可用公式(4)表示：

(4)

其中：m≠1。ε(t)为蠕变过程中土体应变，%；ε0为每级荷载初始时刻应变，%。A、m、α为蠕变模型三参数。

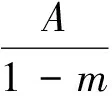
(5)

取对数有：

(6)

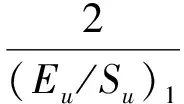
(7)

其中：Eu为初始不排水剪切模量，MPa；Su为不排水剪切强度，kPa；Rf为破坏比，Rf=(σ1-σ3)f/(σ1-σ3)ult。其中，(σ1-σ3)f为实际破坏应力差；(σ1-σ3)ult为最大应力差。λ为模型参数。

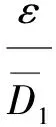
(8)

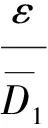
将w=20%、σ3=100 kPa时的试验数据与由以上两种平面蠕变模型所得的模拟值进行比较，对比结果见图7及表2。

由上可知：Singh-Mitchell模型和Mesri模型计算出的拟合曲线均与实际平面蠕变试验值偏离较远，而且差值呈逐渐增大的趋势；在蠕变稳定先期，本文建立的蠕变模型所得的模拟值与实验值存在一定差异，后期模拟值基本接近试验值，相对误差在5%内，且模拟曲线与实际曲线后期趋势吻合。这就说明本文所建立的黄土平面蠕变模型对实际工程的长期蠕变问题有更好的借鉴作用。另外，该模型参数少，拟合精度高，且获得方法简单。

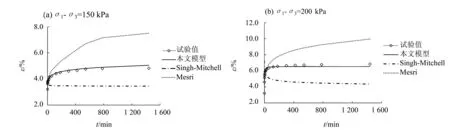
图7 实验值与两种蠕变模型的模拟值Fig.7 Comparison between experimental values and two different creep models

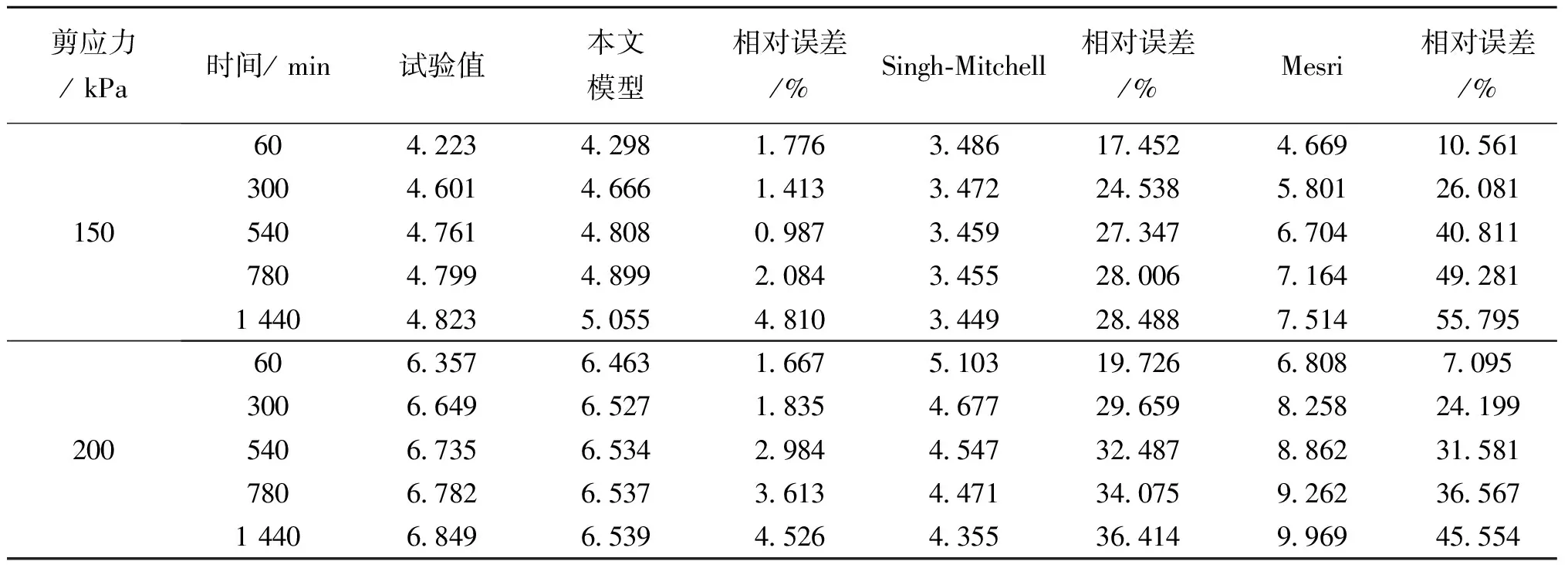
剪应力/kPa时间/min试验值本文模型相对误差/%Singh⁃Mitchell相对误差/%Mesri相对误差/%15060422342981776348617452466910561300460146661413347224538580126081540476148080987345927347670440811780479948992084345528006716449281144048235055481034492848875145579520060635764631667510319726680870953006649652718354677296598258241995406735653429844547324878862315817806782653736134471340759262365671440684965394526435536414996945554

3 结 论

1)本文以蠕变破坏为突破口，以陕西泾阳黄土为研究对象，采用自行改造的平面蠕变仪进行了一系列室内条件下的蠕变试验。改造后的仪器通过控制两平面的应变，可以模拟平面蠕变发生的过程，且改造成本较低，操作简单，可以在无平面蠕变仪器的情况下推广使用。

2)室内试验结果表明：黄土平面蠕变量在大剪应力、高含水率以及低固结压力条件下较大。实际工程中可通过改善边坡排水、增加土体压实固结度来降低工后沉降。

3)本文基于试验数据建立的新平面蠕变模型，参数少，精度高，在模拟实际蠕变过程中，在后期趋势上与实际基本吻合，能够在一定程度反映泾阳黄土的平面蠕变特性。

参考文献：

[1] 刘祖典. 黄土力学与工程[M]. 西安：陕西科学技术出版社，1997：1-3.

LIU Zudian. Loess mechanics and engineering [M]. Xi’an: Shaanxi Science and Technology Press, 1997：1-3.

[2] 李军世，孙钧. 上海淤泥质粘土的Mesri蠕变模型[J]. 土木工程学报，2001, 34(6): 74-79.

LI Junshi, SUN Jun.Mesri’s Creep model for Shanghai silt-clay[J]. China Civil Engineering Journal,2001,34(6):74-79.

[3] 卢萍珍，曾静，盛谦. 软黏土蠕变试验及其经验模型研究[J]. 岩土力学，2008, 29(4): 1041-1044.

LU Pingzhen, ZENG Jing, SHENG Qian. Creep tests on soft clay and its empirical models[J].Rock and Soil Mechanics, 2008, 29(4): 1041-1044.

[4] SIVASITHAMPARAM N, KARSTUNEN M, BONNIER P. Modeling creep behaviour of anisotropic soft soils[J]. Computers & Geotechnics, 2015, 69: 46-57.

[5] 王常明，王清，张淑华. 滨海软土蠕变特性及蠕变模型[J]. 岩土力学与工程学报，2004, 23(2):227-230.

WANG Changming, WANG Qing, ZHANG Shuhua.Creep Characteristics and creep model of marine soft soils[J]. Chinese Journal of Rock Mechanics and Engineering，2004, 23(2):227-230.

[6] WANG J, LIU X, SONG Z, et al. A creep constitutive model with variable parameters for thenardite[J]. Environmental Earth Sciences, 2016, 75(11):1-12.

[7] 刘业科，邓志斌，曹平，等. 软黏土的三轴蠕变试验与修正的Singh-Mitchell 蠕变模型[J]. 中南大学学报(自然科学版)，2012,43(4)：1440-1446.

LIU Yeke, DENG Zhibin, CAO Ping, et al. Triaxial creep test and modified Singh-Mitchell creep model of soft clay[J]. Journal of Central South University(Science and Technology) ，2012,43(4)：1440-1446.

[8] 王琛，胡德金，刘浩吾，等. 三峡泄滩滑坡体滑动带土的蠕变试验研究[J]. 岩土力学，2003, 24(6):1007-1010.

WANG Chen, HU Dejin, LIU Haowu, et al. Creep tests of sliding zone soils of Xietan landslide in Three Gorges Area[J].Rock and Soil Mechanics，2003, 24(6):1007-1010.

[9] 王松鹤，骆亚生. 复杂应力下黄土蠕变特性试验研究[J]. 岩土力学，2009, 30(增2):43-47.

WANG Songhe, LUO Yasheng. Research on creep characteristics of loess under complex stress[J]. Rock and Soil Mechanics，2009, 30(S2):43-47.

[10] MISHRA B, VERMA P. Uniaxial and triaxial single and multistage creep tests on coal-measure shale rocks[J]. International Journal of Coal Geology, 2015, 137:55-65.

[11] ZHOU Z, MA W, ZHANG S, et al. Multiaxial creep of frozen loess[J]. Mechanics of Materials, 2016, 95:172-191.

[12] 郭鸿，陈茜，李军，等. 二维理想颗粒受剪行为的细观机理[J]. 中山大学学报(自然科学版)，2016，55(4)：47-52.

GUO Hong, CHEN Xi, LI Jun, et al. The microscopic mechanism of the shear properties of two dimensional idea particle[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni，2016，55(4)：47-52.

[13] 郭鸿，骆亚生，王鹏程. 分别、分级加载下压实黄土三轴蠕变特性及模型分析[J]. 水力发电学报，2016，35(4)：117-124.

GUO Hong, LUO Yasheng, WANG Pengcheng. Triaxial creep characteristics and models of remodeled loess under separate and graded loading[J]. Journal of Hydroelectric Engineering，2016，35(4)：117-124.

[14] SINGH A, MITCHELL J K. General stress-strain-time function for clay[J]. Journal of the Clay Mechanics and Foundation Division, ASCE, 1968, 94(SM1):21-46.

[15] MESRI G, REBRES-CORDERO E, SHIELDS D R, et al. Shear stress-strain-time behavior of clays[J]. Geotechnique, 1981, 31(4):537-552.

[16] 孙钧. 岩土材料流变及其工程应用[M]. 北京：中国建筑工业出版社，1999：317-335.

SUN Jun. Rheological properties of geomaterials and application to engineering[M]. Beijing: China Architecture and Building Press, 1999. 317-335.

[17] 付中原. 真三轴仪的平面应变改造及黄土平面应变实验研究[D].杨凌：西北农林科技大学，2009：18-21.

FU Zhongyuan. Research on the plane strain transformation of true triaxial equipment and plane strain test of less[D]. Yangling： Northwest A&F University, 2009:18-21.

Planecreepmodelofloess

GUOHong1,LUOYasheng2,HULianxin3,WANGPengcheng3

(1. School of Civil Engineering and Architecture, Shaanxi University of Technology, Hanzhong 723000, China; 2. College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100, China;3.Mecanique, Energétique, Genie Civil et Acoustique, Institut National des Sciences Appliquées, Lyon 69100, France;4.China Construction Municipal Engineering Corporation Limited, Beijing 100071,China)

In geotechnical engineering, agricultural engineering and hydraulic and hydro-Power Engineering etc., many problems such as long-term stability of dam and slope, could be regarded as the plane strain issue. Hence, these questions are always figured out though as the plane creep tests, which are more suitable to the engineering conditions. In order to deeply investigate the plane creep properties of loess soil, a series of laboratory consolidated plane creep tests of loess are conducted by a reformed plane creepmeter in this paper, and the tests results show that the deformation of plane creep is dramatic under high water content, high deviatoric stress and low consolidation condition. Base on the analysis of experimental data, a new empirical model is proposed. In addition, it is found that the two existed models named Singh-Mitchell and Mesri models, which are usually utilized to model the creep problems of soils, are not suitable for loess in the plane strain condition. However, the model proposed in this paper can better describe the creep proprieties of loess in the plane strain condition, due to its merits in both higher accuracy and fewer parameters.

loess; plane creep; creep model

10.13471/j.cnki.acta.snus.2017.06.014

2017-03-01

陕西理工大学人才启动基金(SLGQD2017-03)；国家自然科学基金 (51178392)

郭鸿(1984年生)，男；研究方向岩土工程离散元数值分析；E-mail:aaronkwo@qq.com

骆亚生(1967年生)，男；研究方向黄土力学与工程;E-mail:lyas1967@nwsuaf.edu.cn

TU432

A

0529-6579(2017)06-0094-06