600 kV高压标准电容器的研制*

龙兆芝，李文婷，刘少波，鲁非，张弛，肖凯

（1.中国电力科学研究院计量研究所，武汉430074；2.国网湖北省电力公司电力科学研究院，武汉430077）

0 引 言

高压标准电容器是高压实验室中常用的一种高精度标准装置，具有电容量稳定性好、电压系数小、介质损耗小、不受外界条件影响等诸多优点［1-7］。虽然高压标准电容器一般用于测量工频电压下的电容量和介质损耗，但是用于测量冲击电压信号也具有其独特的优势［8］。冲击电压的测量一般使用弱阻尼电容分压器和电阻分压器，但杂散参数，周围环境和作用电压等因素都能影响这类分压器分压比，进一步提高准确度就很受限制［9-15］。高压标准电容器的结构特点是高低压电极为同轴结构，高压臂电容为平板电容。由于屏蔽电极的存在，高压臂电容不会受到周围带电物体的影响，介质为SF6气体，因此电容量不会随施加电压的幅值和频率变化。因此标准电容器为测量冲击电压信号比电阻分压器和弱阻尼分压器更加稳定。1985年清华大学的戚庆成教授就研究如何利用标准电容器测量冲击电压［8］。

标准电容器整体结构主要有倒立式和正立式结构，目前国内外绝大多数标准电容器采用的电极结构为倒立式结构，这种结构中高压电极包围低压电极，高压电极起到了静电屏蔽作用，避免了电容器受外电场的干扰，所以高低压电极之间电容量可以通过计算公式精确计算［5］。但是低压电极通过长长的测量电缆引出，杂散电感大，测量冲击电压时将在波前叠加较大的振荡。因此测量冲击电压需要研制一种正立式的标准电容器。

因此本文主要介绍一种正立式标准电容器的设计与计算过程。600 kV标准电容器的主要包括均压环、高压复合绝缘套管和接地金属罐体，高、低压电极和屏蔽电极置于金属罐体内部。分压器额定电压：工频600 kV，冲击1 200 kV，保留1.2倍的裕度，在仿真计算过程中工频电压耐压720 kV、冲击电压耐压1 440 kV。高压电容为10 pF×2。高压套管和罐体分压器内部为SF6气体，表压0.4 MPa。

1 .高压套管设计

1.1 套管尺寸

套管采用高压复合绝缘充气套管，主要优点为内绝缘可靠，无局部放电干扰。因此充气套管普遍应用于标准电容器、电压互感器等电气设备上。

（1）套管高度

套管的高度一般由耐受电压计算得到，根据工频干闪耐受电压计算套管高度［16］：

式中Ug为干闪电压，选取工频耐受电压为720 kV；σ为0.05，计算得到两法兰之间的高度Lg=2 848.5 mm

根据雷电冲击电压耐受电压计算套管高度：

其中Uth为冲击耐受电压，选取1 440 kV，σ为0.03，计算得到两法兰之间的高度：Lg=2 748.4 mm。综上所示套管的高度不应小于2 900 mm。

（2）套管直径

套管的直径由套管内、外壁电场强度确定。额定电压下，套管外壁切向电场不大于0.4 kV/mm；在工频耐受电压下，金具允许场强不大于1.2 kV/mm。在SF6中，套管内表面允许切向雷电冲击场强不大于12 kV/mm；雷电冲击耐受电压下，导体及屏蔽表面允许场强为24 kV/mm［16］。使用Ansoft软件对套管进行二维电场仿真计算，选取合适的套管尺寸、高压导杆直径。

如果使用550 kV的高压套管成型产品，高度为4 620 mm，内径480 mm。在工作电压600 kV下对套管进行仿真计算，切向最大场强为0.9 kV/mm，不满足电场限值要求。不断将接地屏蔽的位置往高压导杆方向移动将使腔体内的电场强度过大。因此需要增大套管内径，最终将套管的内径增大至600 mm，高度为5 000 mm。

（3）高压导杆

同轴圆柱电场中的中心导体表面场强由式（3）计算：

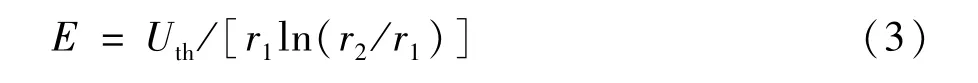
式中E为电场强度；Uth为雷电冲击耐受电压（kV）；r1为高压导杆半径（mm）；r2为下法兰半径（mm）。

其中r1/r2在0.222至0.535的范围内变化时，导体表面场强之变化10%，因此上式可简化为：

式中E1为对应某种SF6气体导体表面允许的雷电冲击场强，取24 kV/mm，计算得到高压导杆的半径为60mm。

1.2 套管屏蔽设计

（1）接地屏蔽的设计

从改善套管下端内电场分布及套管外电场分布的两点要求出发，通常按下面经验公式初步确定内屏蔽筒高度h为：

式中r2为套管内径300，取1 200 mm。

（2）中间电位内屏蔽的设计

套管的电压大于500 kV，需要设计中间电位屏蔽。中间电位屏蔽主要是为了改善套管外壁电场分布，否则套管下半部分电位梯度太大，电场集中于套管下端［17］。采用中间电位屏蔽，强制性地将某一中间电位U0推至套管中间位置，从而使套管外壁电场分布趋于均匀，还可以改善下法兰处内电场的分布。

图1为高压套管结构图，从图中可以看出高压导杆与中间电位屏蔽间的电容为C1，中间电位屏蔽与接地屏蔽之间的电容为C2，中间屏蔽对罐体的电容为C3，中间电位屏蔽上的电压为C2+C3上分得的电压，U0=U·k，其中U为高压导杆电压，k为电压系数［14］：

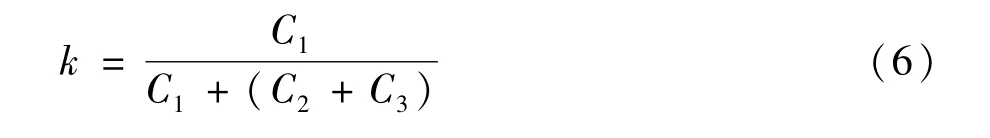
图2 套管外壁电场和电压分布曲线Fig.2 Distribution curves of voltage and electical field outside the bushing from bottom to top

套管外壁电场强度分布曲线如图2（a）所示，从图中可以看出套管外壁从下至上电场强度有两个峰值，最大电场约为0.5 kV/mm。图2（b）为套管外壁电压分布曲线，从图中可以看出，图中虚线为理想的电压分布曲线，实际电压曲线沿该直线分布，有效利用了套管的高度。电压分布在接地屏蔽的上部和中间电位屏蔽的上部对应尺寸处，套管外壁的电压上升斜率增大，与电场强度峰值位置对应。此时中间电位屏蔽上的电压系数k=41.6%，符合经验值40%～45%［15］。

接地屏蔽和中间电位屏蔽采用不锈钢材料，通过超精磨对屏蔽层表面做镜面处理，表面粗糙度＜0.2μm。但相对于铝件，不锈钢材料的重量较大，对固定中间电位屏蔽绝缘件的支撑强度要求更高，相对于类似盆式绝缘子的锥形筒，使用L形的环氧法兰的强度更好，图3为支撑法兰内部的电场云图，从图上可以看出，环氧法兰内部最大电场为2.3 kV/mm，小于规定值3 kV/mm。

图3 中间电位屏蔽支撑绝缘件内部电场Fig.3 Internal electric field distribution of insulation support

2 电极设计

2.1 高、低压电极

根据物理学公式，同轴结构电容器的电容量计算公式为：

式中 真空介电常数ε0=8.854×10-12；εr为介质的相对介电常数，在0.4 MPa的SF6气体环境中为1.008；r2为低压电极半径；r1为高压电极半径；电容值C取10 pF。该式中有l、r1、r2三个变量，为了计算方便，先确定l=55 mm，同时引入同轴结构内电极最大场强计算公式：

式中E为高压电极表面允许的最大电场强度；U为施加在高压电极上的电压。

式（7）、式（8）为雷电冲击电压和工频电压下，SF6内部导体表面最大允许电场的计算公式［5］：

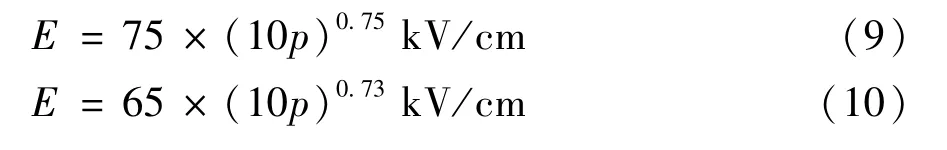
式中p为气压，单位为MPa。取一定的裕度，r1=278 mm，便可求得r2=390 mm。而低压电极与屏蔽罩相邻处场强大小由于相互作用无法计算，而该处的场强值又发生畸变，为了保证各点电场值低于基准值，需利用Ansoft仿真软件辅助对低压电极的半径进行调整，同时为了满足电容量要求，对低压电极高度进行调整［18］。

为了改善低压电极边缘处电场分布，会对其边缘部分做圆弧处理，但在仿真计算中，低压电极表面的电场将影响电容值，因此需要不断均匀电场调整低压电极的长度，改变正对面积。计算中将整体电容量按照低压电极的结构，分为圆弧部分和非圆弧两部分处理，两部分电容量之和为整体电容量。计算过程中在Ansoft中提取整体电容量CA，求出需增加的电容值ΔC=C-CA=10-CA。

由该值，利用同轴电容器计算公式：

计算得到增加非圆弧部分长度Δl。

由l、r1、r2的计算结果作为优化调整的依据，利用仿真软件辅助调整，最终以电容量，场强值，结构、安装方式等角度确定各值是否合适，否则调整。最终确定r1=278 mm，r2=390 mm，l=56 mm，单个电容量计算值为9.94 pF。

2.2 屏蔽电极

屏蔽电极在设计上最大程度的包围低压电极，从而使得低压电极上的电场相对均匀，同时屏蔽外部带电体对高压电容的影响。因此屏蔽电极采用多弧度相连的形式，此外应尽量缩短屏蔽电极与低压电极之间的距离，提高屏蔽效能。在实际安装时，分上下两部分固定在环氧筒上。环氧筒安装在罐体底面，为保证同轴度，在底面刻槽与支撑绝缘子保证同心，以提高电容量的稳定性［16］。低压电极安装在屏蔽电极上，使用绝缘支柱保证距离。低压电极与屏蔽电极的距离为3 mm。

2.3 电场分布

图4为电极内部电场云图，从图中可以看出，高压电极与低压电极之间的电场分布非常均匀，最大电场出现为高压电极上下圆弧处为18.1 kV/m，低压电极表面无电场突变，最大电场约12 kV/mm。图5为标准电容器电位线分布图，施加电压720 kV，从图中可以看出在套管表面，电位线分布非常均匀，无非常集中之处。

图4 标准电容器内部场强云图Fig.4 Internal field strength cloud diagram of standard capacitor

图5 电力线分布Fig.5 Distribution of power line

3 支撑绝缘子设计

在设计中，高压电极与壳体之间支撑选用环氧浇铸绝缘子，要求工作电压下，绝缘件内部及嵌件允许工作场强不大于3 kV/mm，雷电冲击试验电压下，绝缘件表面电场不大于12 kV/mm。为了确定绝缘件的长度，先利用经验公式（12）确定绝缘件的初步尺寸，而后利用仿真软件对其电场分布进行仿真计算，最后确定绝缘子的尺寸。

式中K3为绝缘支撑电场分布不均匀系数，K3=1.5～2.0，本设计中选取2.0；K4为安全系数，K4=1.4～1.8，本设计中取1.8；Eτ为绝缘子表面允许场强，取12 kV/mm；U为冲击耐受电压峰值，为1 440 kV，计算值为432 mm。

由于绝缘子是装在高压电极内部，为了保证高压电极的稳定性将安装部位选在高压电极下二分之一处，同时又要保证高压电极下端与底面之间的间距，经仿真计算，最终确定支撑绝缘子高度为450 mm，图6为支撑绝缘子内部的电场云图，绝缘子内部及嵌件处最大场强为1.7 kV/mm＜3 kV/mm［16］，满足设计要求。

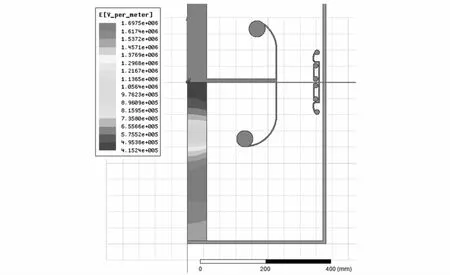
图6 底部绝缘支撑内部电场分布Fig.6 Internal electric field distribution of bottom insulation support

4 电容器的性能

影响标准电容器电容量的稳定性的主要因素为气压、温度、电压［16］，其中气压主要影响标准电容器内部SF6气体的介电常数，在一定范围内SF6的介电常数与气体压力的升高线性增大，但该标准电容器的内部压力为0.4 Mpa，影响气压的变化主要因素为温度，由于电容器不产生热量，因此只有外界温度变化对气压存在影响，且其影响非常小，可忽略不计。

温度主要影响介电常数、内部压力、电极形变，另外湿度也将影响介电常数随温度的变化规律，因此在充气时，需要进行干燥处理。压力恒定时，气体的介电常数的温度系数负，假设干燥气体介电常数的温度系数约为-1×10-5，则引起电容量的变化量约为-1×10-10，可忽略不计。温度升高，将引起电极直径和长度的延伸，对于圆柱形电极，主要考虑长度的延伸，导致电容量增大，因此电容量的温度系数主要取决于电极的金属膨胀系数，电容温度系数为正值，铜和钢的膨胀系数约为20×10-6m/K。

电压主要表现为电场力使得电极相互吸引，距离减小，电容量增大，电压系数为正，与材料的弹性模量有关，不锈钢材料的弹性模量为2×1011N/m2。另外由于安装时不能保证绝对同轴，偏心将使得电容量发生变化。由于电极的受力与电场的平方成正比，因此其关系式为二次多项式。

4.1 温度系数

假设圆柱形电容器各部分温度均匀，且圆柱筒的径向热膨胀是从中间位置相两边均匀膨胀［19］，设内圆柱筒的外半径r1向外增加Δd1/2，而外圆柱筒的被半径r2向内减小Δd2/2，在温度变化时：

高压电极壁厚增量为：

低压电极壁厚增量为：

因此温度变化后高压电极与低压电极的半径为：

式中T为温度；α为材料的线膨胀系数20×10-6m/K；d1为高压电极厚度3 mm；d2为低压电极厚度2 mm；r1为高压电极外径278 mm；r2为低压电极内径390 mm。设置T从0℃～100℃变化时温度对引起的电容相对变化量曲线如图7所示，从图中可以看出，有温度引起的误差与温度成正比，温度系数为正。计算得到温度系数为2.05×10-5/K。

4.2 电压系数

（1）电场力的影响

根据文献［3］提出的静电场力对电容量的影响，电场力变现为高压电极和低压电极之间的吸引力，使得高压电极半径增大，低压电极半径减小。其中r1的变化Δr1为：

图7 温度引起电容相对变化量曲线Fig.7 Relative change curve of capacitance caused by temperature

式中C为电容量9.94 pF；U为施加电压600 kV；l为正对长度56 mm；r2为低压电极半径390 mm；r1为高压电极半径278 mm；d1为高压电极厚度3 mm；d2为低压电极厚度2 mm；E1为高压电极材料弹性模量2×1011N/m2；E2为低压电极材料弹性模量2×1011N/m2。计算得到600 kV时电容量的电压系数为5.5×10-7。

（2）偏心的影响

在高压电极和低压电极安装时将导致偏心的现象，使得高压电极和低压电压中心轴不重合也会使电容值发生变化。假设两圆筒中心轴平行，轴间距离为b则两电极不同轴引起的电容量的变化为［20］：

5 结束语

（1）高压套管外壁自下至上电场强度分布曲线具有两个峰值，分别在接地屏蔽上部对应的高度以及中间电位屏蔽上部对应的高度。中间电位屏蔽上的电压系数越高，地电位屏蔽罩上端对应的高度处场强增大，中间电位屏蔽罩上端对应的高度处场强减小；

（2）均匀合成电场曲线上的两个峰值时套管外壁电压分布曲线更接近理想曲线，此时电压系数k为41.6%，此时中间电位屏蔽表面最大电场为7.4 kV/mm；

（3）600 kV标准电容器在雷电耐受电压1 440 kV下，标准电容器内部最大电场为18.1 kV/mm，分布在高压导杆与高压电极下圆弧处。低压电极表面电场分布均匀，内部绝缘支撑内部电场小于2.3 kV/mm。电容量均为9.94 pF，为了改善动态特性，低压电极与罐体内壁的距离为15 mm；

（4）影响标准电容器电容量的稳定性的主要因素为气压、温度、电压。根据标准电容器的尺寸和材料，计算得到温度系数为2.05×10-5/K，600 kV时的电压系数为5.5×10-7。由偏心引起的电容量的变化为3.95×10-5，但安装时该误差已经固定。对于强抗弯强度的材料，静电场力加剧偏心时引起的电容量变化可忽略不计。