利用小波能量特征的增长型自组织神经网络同调机组分群方法*
杨越,王涛,顾雪平,岳贤龙,徐振华,邱丽君
(1.华北电力大学新能源电力系统国家重点实验室,河北保定071003;2.国网福建省电力有限公司电力科学研究院,福州350007;3.中国电力科学研究院,北京100192)
0 引 言
电力系统中发电机功角不是一成不变的,而是随着外界扰动和运行状态的变化而变化,发电机功角在变化过程中,不同的机组可能具有一致的动态变化特性,即机组之间存在着同调现象[1]。可以依据电力系统中机组之间的同调性将整个系统分成各个互相解耦的子系统,进而简化系统模型。比如:当系统发生低频振荡时,若存在着弱互联区域,通常应用机组之间的同调现象将系统分区域研究[2];在EEAC法中,也是先进行发电机的两群假设,将发电机分为临界机群和剩余机群[3]。除此之外,当电网受到大冲击,为了避免发生连锁故障[4]、防止大停电而进行的解列控制[5]也多以同调机组分群为基础。所以精准识别电力系统的同调特性具有重要意义。
目前,机组分群方法主要有两类,第一类是建立系统发电机模型,然后选出一个反映系统发电机同调性的参数,根据参数的相似程度进行分群;第二类是仿真扰动后发电机功角的变化趋势,通过辨识功角摇摆曲线相似程度进行同调分群。其中第二种方法应用越来越广泛,很多学者采用时域分析、频域分析、时频分析来确定发电机功角摇摆曲线的相近程度。时域分析方法主要包括提取时域特征[6]、曲线相关分析[7]等。为了获得更精确的反映发电机功角摇摆曲线趋势的特征,一些学者利用频域分析方法,采用傅里叶变换来提取频谱分布特征[8]。时域分析能够提取分辨率很高的时域特征,但是频域分辨率却很低,频域分析能够提取分辨率很高的频域特征,但是时域分辨率却很低,都不能全面准确提取功角摇摆曲线的特征。为此,很多学者利用时频分析来提取功角摇摆曲线特征,小波变换就是其中的典型代表。小波变换结合了时域分析和频域分析的优势,在高频部分具有很高的时间分辨率,在低频部分具有很高的频率分辨率,提取的特征能够全面准确地反映功角摇摆曲线特性[9]。文献[10]采用小波分解方法将功角摇摆曲线分解为高频信号和低频信号,并且将低频信息进行重构,将重构的信息进行相关性分析,这种方法既缩减了信息维数,又去除了信息噪声,通过摇摆曲线基本升降规律识别同调机群,但是此方法计算量大。
同调机群的识别其本质是一个聚类问题,即将同调的机组聚集在一起,不同调的机组分开。同调机组的聚类方法主要包括相关系数法[11]、层次分析法[12]、模糊聚类法[13]等。对于大系统而言,这些方法一般比较复杂,计算量大,不适合于大数据的处理。文献[14]提出把Kohonen自组织神经网络运用到同调识别,适合大数据的处理,但是需要预先指定竞争层网络单元数目及其机构形状。
考虑到同调机群识别中存在的上述问题,首先使用小波变换的多尺度空间能量分布特征的提取方法提取机组功角摇摆曲线特征向量,然后将小波能量特征和时频域特征组合,作为增长型自组织神经网络的输入向量,在保证信号特征全面的情况下降低了特征的维度,通过控制阈值λ,最终在输出层得到不同精度的分群结果。最后通过10机IEEE-39节点系统验证了此方法的计算量小,计算速度快,聚类结果具有更高的稳定性和准确性。
1 同调机组分群理论
发电机的同调性是指当系统运行方式改变或受扰后,系统中发电机功角变化呈现出相似的规律[15]。关于同调机群的定义多种多样,最常用的定义如下,在计算时间t∈[0,T]内满足:
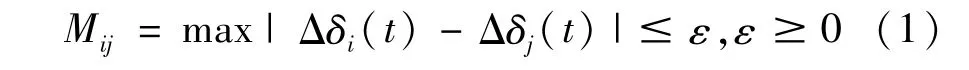
式中 Δδi=δi-δi0;Δδj=δj-δj0;δi、δj为发电机i、j的实时功角;δi0、δj0为发电机i、j的功角初值;Δδi、Δδj为发电机功角的实时变化量;ε是发电机之间同调程度的度量值。
但考虑到当两台机组i,j摆幅都很小,并且一台机组摇摆曲线上升,另一台机组摇摆曲线下降的情况下也很有可能满足式(1),而此时两台机组明显不同调。因此利用相关性来定义机组同调:
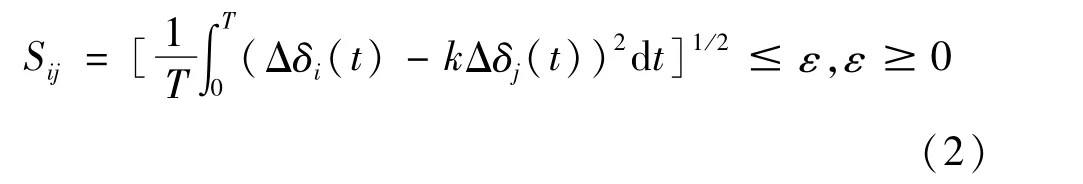
k可以取任意常数使得Sij最小,令:

可求出:

综合式(1)和式(4),定义机组同调识别判据为:

式中α为最大最小原则比重系数;β为均方根准则比重系数(本文取α=0.6、β=0.4)。当ε=0时,即发电机功角摇摆曲线走向完全一致,称发电机完全同调;当ε>0,即发电机功角摇摆曲线最大差为ε,称发电机ε-同调。在实际应用中,没有完全同调的发电机,所以一般使用ε-同调。
将满足式(5)的发电机视为同调机组,不满足式(5)的发电机视为不同调机组,这样通过划分外在功角摇摆曲线实质划分发电机内在特性的过程就是机组同调识别。
2 小波能量特征提取
以短时傅里叶变换为过渡发展起来的小波变换,同时具有良好的时域趋势描述、频域局部特征刻画功能,克服了傅里叶变换在时域上不能定位的缺点,并且小波的选取非常灵活,适合分析瞬时非平稳信号,被广泛应用于特征提取[16]。
对功角摇摆曲线在多尺度空间进行小波分解,信号被分解为多个频段,低频段之前的系数为逼近系数,高频段之前的系数为细节系数,合称为小波系数,它们蕴含着大量反映摇摆曲线特征的信息。通过小波系数计算各个频段的小波能量,并且按频次由大到小的顺序排列,构成小波能量特征向量,这就是小波变换多尺度空间能量分布特征的提取方法[17]。
假设f∈L2(R)是发电机的功角摇摆曲线,测量信号fj是f在尺度空间Vj的近似,则fj的多尺度分解可表示为:式中fj-k和wj-k分别为fj在空间Vj-k和Wj-k的逼近和细节。

为了计算快速方便,采用二进小波变换中的Mallat算法实现[18]。利用Mallat算法对功角摇摆曲线逐层分解,每一层的逼近系数通过一组高通滤波器和低通滤波器得到下一层的逼近系数和细节系数[19]。功角摇摆曲线f(k),k=1,2,...,M,其二进小波分解Mallat算法如下:

式中M是功角摇摆曲线f(k)的采样点数;j是分解的层数;hn-2k,gn-2k分别是低通滤波系数和高通滤波系数;分别是功角摇摆曲线f(k)在分辨率2j-1下的逼近系数和细节系数;
对功角摇摆曲线f(k)进行两层小波分解,被分解为三个频段,其中逼近系数为Ca2,细节系数为Cd1、Cd2。
提取小波变换多尺度空间能量特征的步骤如下:
首先给出小波能量定义,功角摇摆曲线f(k)在子空间Wj中小波能量定义为:

(1)确定信号各频段小波系数的总能量,如下:
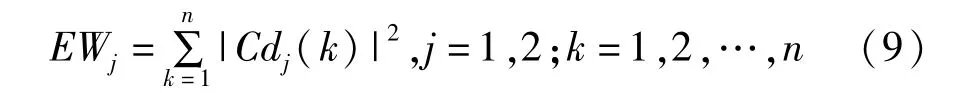
(2)构造小波能量特征向量。依次计算各个频段的小波能量值,并且按照频段顺序排列组合为特征向量:

利用上述流程可以对机组功角摇摆曲线信号进行特征提取,提取出可以代表摇摆曲线的特征向量数据。即完成从摇摆曲线信号到特征向量数据的转换。
3 自组织神经网络模型学习算法
增长型自组织神经网络不需要事先设定竞争层神经元的个数,而是随着阈值λ的改变,自动生成不同数量的竞争层神经元。该方法不受样本输入顺序的影响,聚类结果准确稳定,被广泛应用于聚类分析[20]。
3.1 增长型自组织神经网络结构
自组织神经网络和一般神经网络相比,没有隐含层,只有由权值连接的输入层和竞争层。如图1所示。输入层输入样本的特征向量,其中输入层神经元的个数等于样本特征向量的维数。竞争层输出样本的分类结果,竞争层神经元的个数等于最终的分类组数。竞争层神经元个数是逐渐变化的,随着输入样本的增加,样本属于不同类别的数量就会增加,竞争层神经元的个数也就跟着增加。
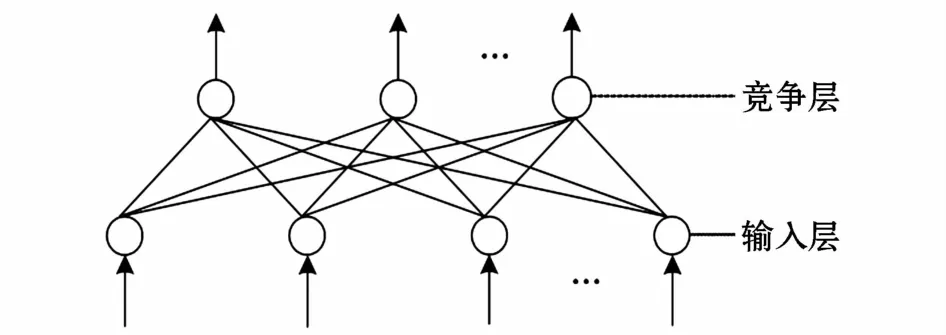
图1 自组织特征映射神经网络结构图Fig.1 Self-organizing neural network structure diagram

式中Xi为输入向量;Wij为第j类组别模式的聚类中心;Dj为欧氏距离。
3.2 增长型自组织神经网络学习算法
增长型自组织神经网络属于无导师学习型网络,不需要先验知识的引导,自动形成组群分类。该算法主要包括以下步骤:
(1)设置阈值λ。λ可以控制聚类结果的精细程度,聚类结果随着λ的增大而变粗。在聚类前,通过试算λ值以应对不同聚类情况;
(2)初始化权值。样本输入特征向量为:Xi=[xi1,xi2,...,xiN]T;N是样本输入特征向量维数;i为样本数量。初始令竞争层神经元个数为j=1,将任意样本输入特征向量作为输入层与竞争层的连接权值Wij;
(3)竞争分类。输入一个新的样本,计算其与竞争层神经元的欧氏距离Dj,欧式距离最小的竞争神经元p获胜:Dp=min{Dj};
(4)更新权值。如果Dp<λ,则将该样本纳入竞争神经元k代表的组别模式,同时更新连接权值:Wij(n+1)=Wij(n)+η(n)(Xi-Wij(n)),η(n)是纳入第j个动态类型纳入样本数的倒数。然后转入第(3)步;
(5)更新竞争层。如果Dp>λ,则该样本不纳入任何一个竞争神经元代表的组别模式,并且更新竞争层神经元数量j=j+1,该样本代表新的组别模式,
输入层与竞争层中的连接权值起着中心指引的作用,相当于整个自组织神经网络的分析系统,能够记忆每个竞争神经元代表的组别模式,随着样本划分到不同的竞争神经元,新增样本的竞争神经元的连接权值也要更新。当一个样本的特征向量与一个竞争神经元的连接权值相似到一定程度时,那么该竞争神经元就将其纳入本组,否则,该样本不属于任何现有竞争神经元,需要新增一个竞争神经元,并用其连接权值记忆新的样本模式[21]。
增长型自组织神经网络样本输入向量为N个功角摇摆曲线的特征,竞争层神经元不断更新的连接权值称为该模式组别的聚类中心,根据输入特征相似程度将样本划分到不同的组别模式中,使得功角摇摆曲线变化趋势相似的发电机聚集在一起,不同的分开,输入向量和组群中心的相似程度用距离来衡量,本文采用欧氏距离[22]:新组别模式与输入层的连接权值Wij(n+1)为该样本输入特征向量;
(6)依次循环。当全部样本被纳入竞争神经元结束。竞争神经元个数j就是聚类组数,每个竞争神经元纳入的样本为具体分类结果。
上述增长型自组织神经网络学习的过程就是神经网络的构建模型的过程,当有新的实时样本时,只需将新样本输入模型,在竞争层即可得到最终的分类结果,每个竞争神经元代表不同的组别模式。
3.3 最优阈值λ的确定
当给定一个λ值时,系统机组被划分为K类,即将系统中时序功角数据集 D={d1,d2,…,di,…,dN}划分为K个簇{C1,…,Cj,…,CK},其中di∈Rm;N为系统发电机数量;m为时序功角向量维度。每个簇都有各自的聚类中心cj,计算所有簇内各个数据点到聚类中心cj的欧式距离的平方和J(C),其函数值的大小反映了聚类结果的优劣。
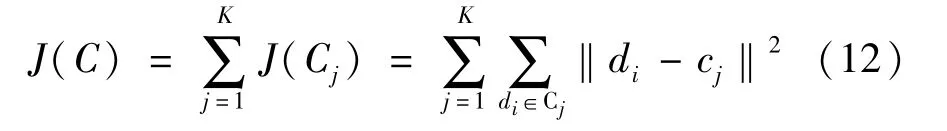
显然,每个K值都对应一个函数值J(C)。当K值较小时,每个簇的欧氏距离很大,随着K值的增大,函数J(C)减小的非常快。此时样本快速分堆,具有相似特性的样本聚集在一起,聚类效果迅速优化;当K值较大时,每个簇的欧式距离已经很小,继续增大K值,函数J(C)的变化将不再明显,此时聚类结果已达到最优。J-K关系曲线如图2所示,图中的拐点可确定最优的分类K值,进而根据该分类K值就可以得到最优的阈值λ。

图2 J-K关系曲线Fig.2 J-K relationship curve
4 算例分析
4.1 同调机群识别流程
选取发电机功角曲线的局部超调量d1ij和全局能量d2ij作为功角摇摆曲线时域特征[6];选取发电机功角曲线的主频成分ωmax作为功角摇摆曲线频域特征;根据上述小波能量特征提取方法,构建小波能量特征向量 F=[Ei0,Ei1,Ei2]。综合时频域特征、小波能量特征,构成神经网络发电机样本输入向量为:G*i=[d1ij,d2ij,ωmax,Ei0,Ei1,Ei2],并且将其归一化:

以PSD-BPA为电力系统仿真平台,模拟线路出现故障模式,对电力系统进行故障模拟仿真。根据上文所诉内容编写计算机程序。程序流程如图3所示。
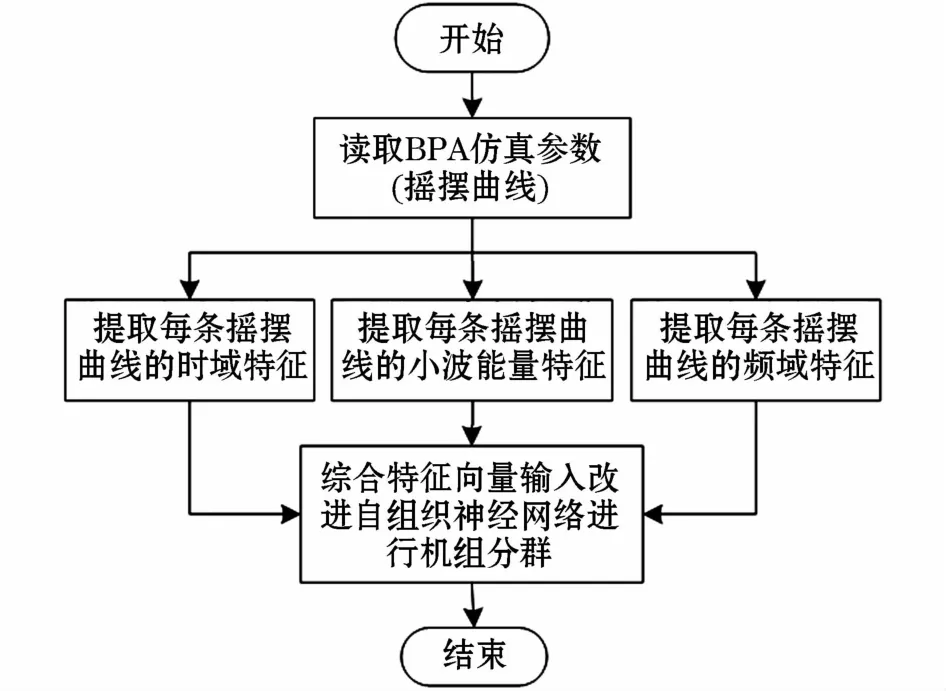
图3 程序流程图Fig.3 Program flow chart
4.2 IEEE-39节点仿真分析算例
为验证本文方法的有效性,以IEEE-39节点系统为例进行聚类分析,该系统包括39个节点,10台发电机,其中31号发电机节点为平衡节点,30、32、33、34、35、36、37、38、39号发电机节点为 PV节点,负荷为恒定阻抗。IEEE-39节点系统如图4所示。
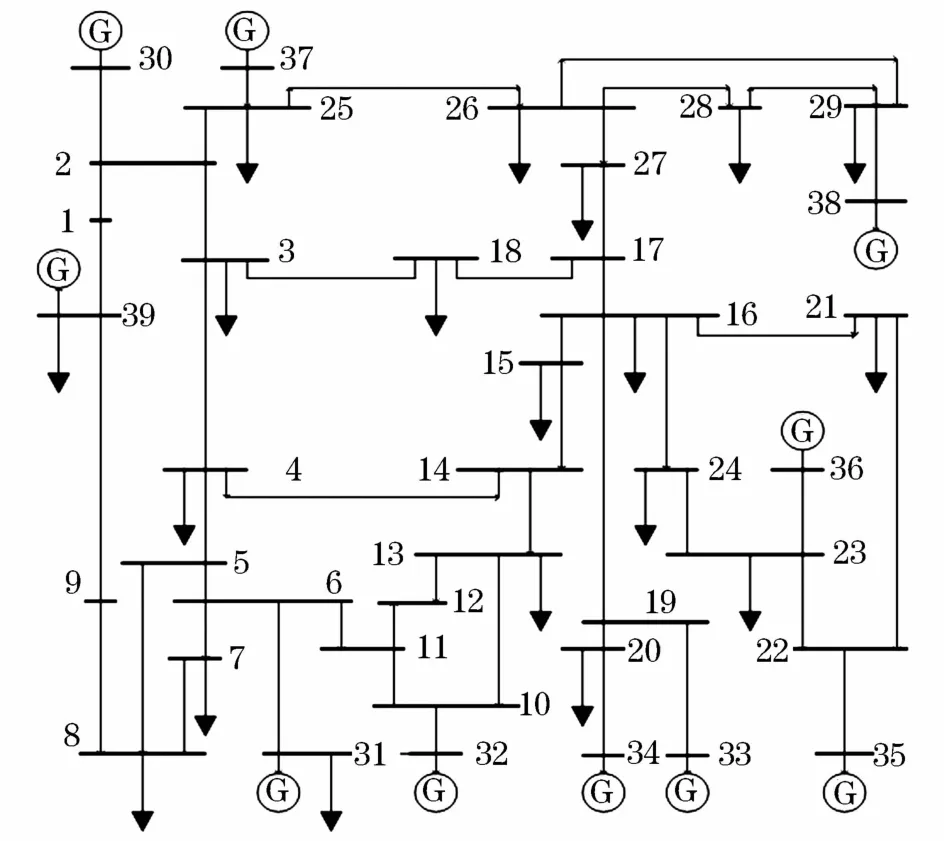
图4 IEEE 39节点系统接线图Fig.4 Wiring diagram of IEEE 39-bus system
分别以发电机G30、G32为参考机,设BUS-3处发生三相断路故障,故障持续时间0.12 s。切除故障前后网络的拓扑结构保持不变。在BPA中得到每个发电机的功角变化数据,并经过Matlab处理后分别如图5、图6所示。

图5 IEEE 39发电机功角摇摆曲线Fig.5 IEEE 39 generators power angle of the rocking curve
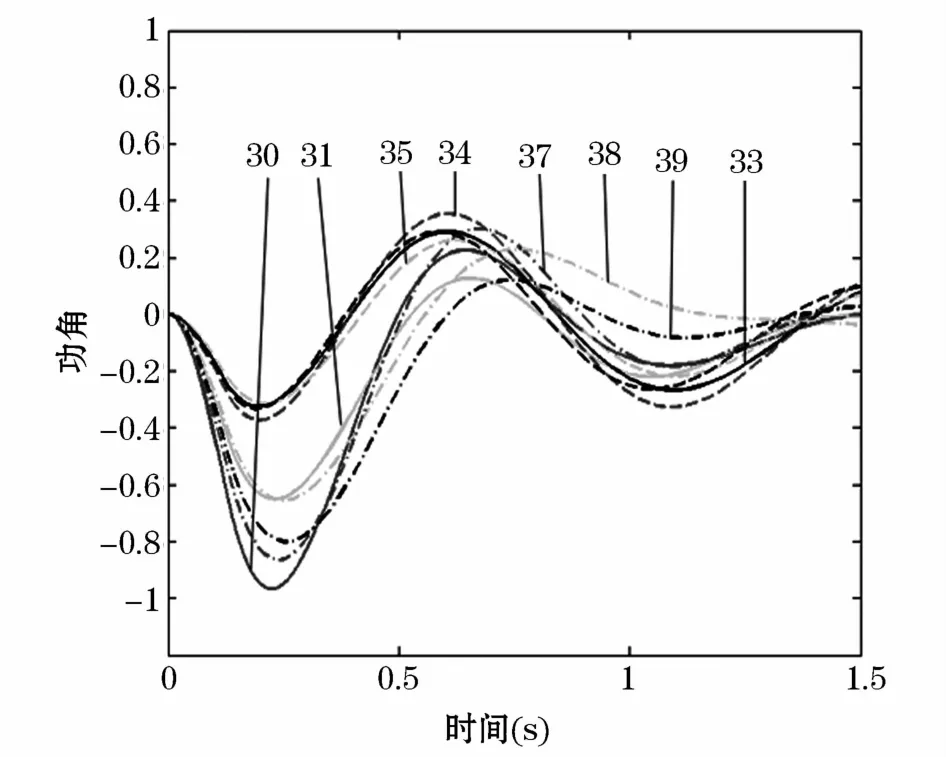
图6 IEEE 39发电机功角摇摆曲线Fig.6 IEEE 39 generators power angle of the rocking curve
样本参数为S={G30,G31,G32,...,G39}。首先只考虑时频域特征作为特征向量,构成10×3特征参数矩阵,将其输入自组织神经网络进行训练,得到的识别结果如表1所示;然后同时考虑小波能量特征和时频域特征作为特征向量,构成10×6特征参数矩阵,将其输入增长型自组织神经网络进行训练,得到的识别结果如表2所示。
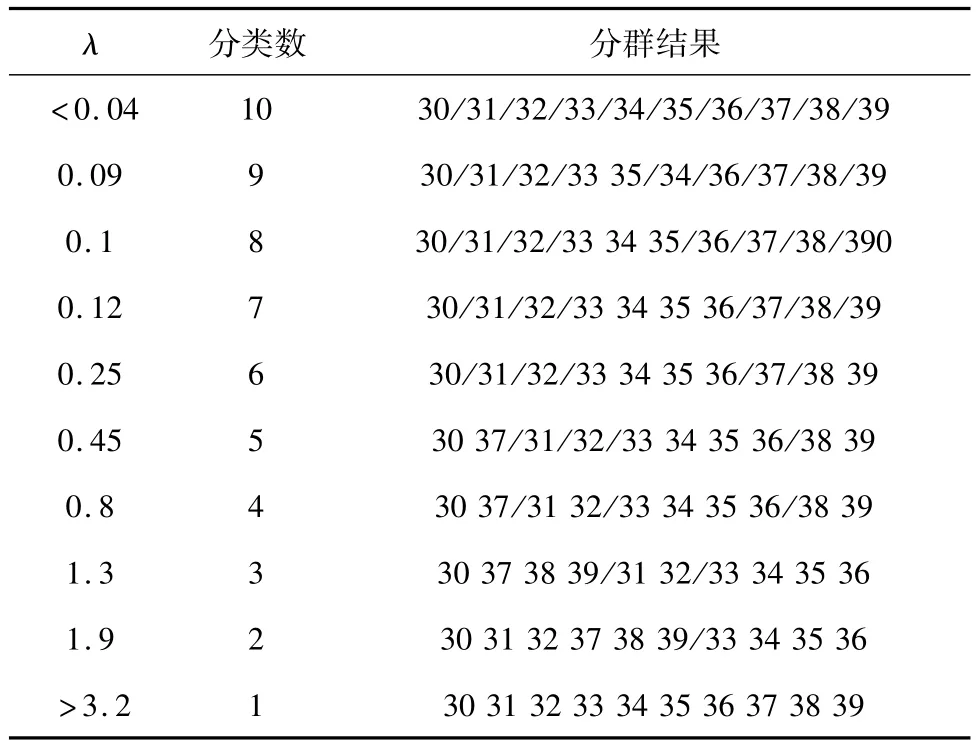
表1 只考虑时频域特征的同调机群划分结果Tab.1 Coherent cluster division results when considering only the frequency domain characteristics of the coherent cluster division results
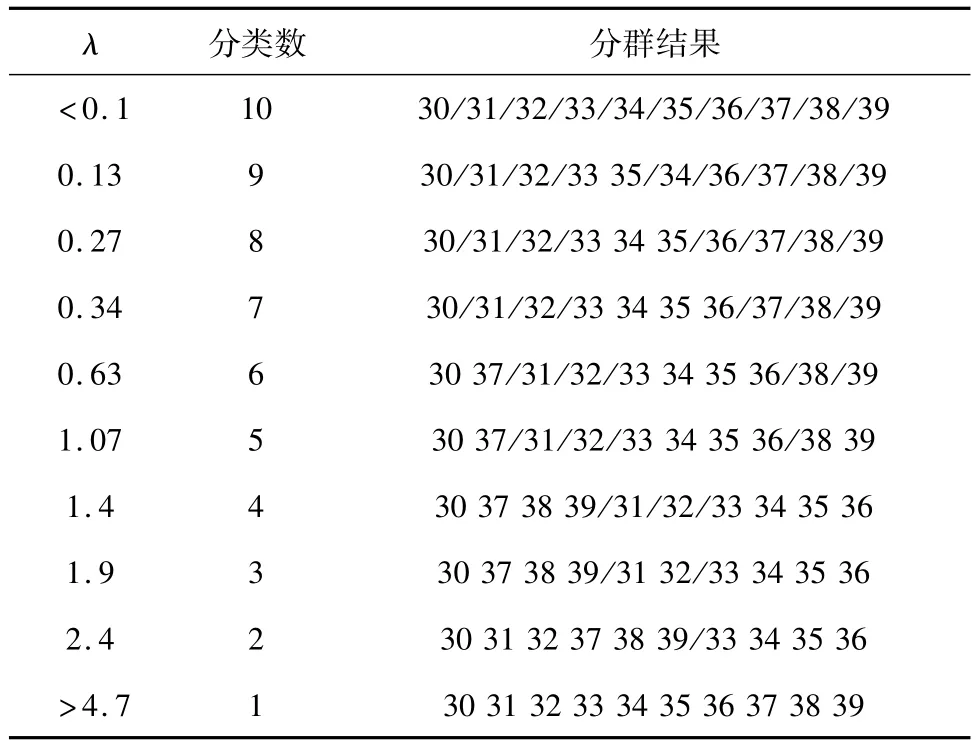
表2 同时考虑小波能量特征和时频域特征的同调机群划分结果Tab.2 Coherent fleet division results when taking into account the characteristics of wavelet energy and time frequency domain features coherent fleet division results
从表1可以看出,当分类数为6时,只考虑时频域特征的分类结果为:{30}{31}{32}{37}{33,34,35,36}{38,39}。从表2知,同时考虑小波特征和时频域特征且分类数为6时,分类结果为:{30,37}{31}{32}{33,34,35,36}{38}{39}。按式(5)计算的同调判据值进行分析,1.5 s之内G38、G39同调判据值为0.075,G30与G37的同调判据值为0.053 5,G30与G37的同调性要强于G38与G39,从图6也能直观看出来,G30、G37的同调性明显比G38、G39更强。因此,同时考虑小波特征和时频域特征的分群结果更为合理。
当分类数为4时,只考虑时频域特征,分类结果为{30,37}{31,32}{33,34,35,36}{38,39}。同时考虑小波特征和时频域特征的分类结果为{30,37,38,39}{31}{32}{33,34,35,36}。在1.5 s之内G31、G32按式(5)计算同调判据值为0.270 6。而G30、G37、G38、G39相互之间按式(5)计算的同调判据最大值为0.148 0。可见,将{30,37,38,39}聚为一类是合理的。因此,同时考虑小波特征和时频域特征的分群结果明显要优于只考虑时频域特征的分群结果。
综上所述,同时考虑小波能量特征和时频域特征比只考虑时频域特征作为增长型自组织神经网络输入向量具有更高的准确性,验证了所提出的方法更为有效。
5 结束语
提出了一种新的基于小波变换多尺度空间能量分布特征和增长型自组织神经网络的同调机组分群方法。改进了同调机群识别的判据,利用小波变换多尺度空间能量分布特征的提取方法提取机组功角摇摆曲线信号的特征,并结合时频域特征构成输入特征向量,减少了特征维数。利用融合自适应共振理论和Kohonen网络基本思想改进了自组织神经网络,克服了自组织神经网络需要预先给定竞争层网络单元数目及结构形状的问题。仿真算例可以看出,同时考虑小波能量特征和时频域特征的聚类方法比只考虑时频域特征具有更高的聚类准确性。

