一种用于柔性直流输电系统的能效计量方案*

章江铭，胡瑛俊，姚力，韩霄汉，沈曙明，杨瑶佳

（1.国网浙江省电力公司电力科学研究院，杭州 310014；2.武汉大学 电气工程学院，武汉 430072）

0 引 言

上世纪90年代以后，柔性直流输电技术受到了业界的重视并得到了快速的发展。相比于传统直流输电技术，其优势主要体现在：可对有功和无功功率进行独立调节控制，方便潮流反转；作为电网恢复启动电源进行故障电网快速恢复；换流站之间可相互独立控制，无需通信；在同等容量下，换流站占地面积显著小于传统高压直流换流站；交直流侧谐波均大为减少等优势［1］。柔性直流输电技术虽有许多技术优势，并得到较快发展，但也存在对系统损耗无法进行准确计量的缺陷，限制了柔性直流输电系统的进一步发展应用。

文献［2］提出一种针对换流器损耗的直接测量方案，将两个换流器进行短暂的背对背操作连接，但整流器和逆变器引起的损耗不能进行区分。文献［3］提出一种换流器损耗的测量方法，用于确定系统的效率，但需要在交直流两侧都配置计量用的电流互感器和电压互感器，并采用多通道宽带功率分析仪以确定交流和直流电能，操作复杂；而且目前直接测量直流大电流存在困难以及尚未建立完整直流大电流计量体系，从而无法进行有效量值溯源［4-6］。在南澳多端柔性直流输电系统中［7］，换流站大量使用光电式电压、电流互感器，但其中大多数互感器都是用于控制保护用，精度要求相对较低，不能满足能效计量的要求，且所需要的计量装置较多，安装复杂。

因此，本文提出一种柔性直流输电系统能效计量方案，通过对系统各个设备损耗的理论计算，结合能耗率、经济性、谐波影响等因素，确定相关能效计量点的选择，并根据误差传递理论分析了计量装置的准确度等级要求。该方案有利于掌握不同工况下柔性直流输电主要设备及系统整体能耗，为今后改进柔性直流输电系统设备工艺水平、系统运行方式提供技术支撑。

1 典型柔性直流输电系统拓扑结构

典型柔性直流输电系统拓扑结构如图1所示，其中，换流阀G1工作在整流状态，换流阀G2工作在逆变状态，系统一般采用双极运行方式。每个换流站都包括联结变压器、接地电抗器、桥臂电抗器、换流器、平波电抗器、直流电容、直流电缆等。这些元件在电流通过时均会产生能耗。

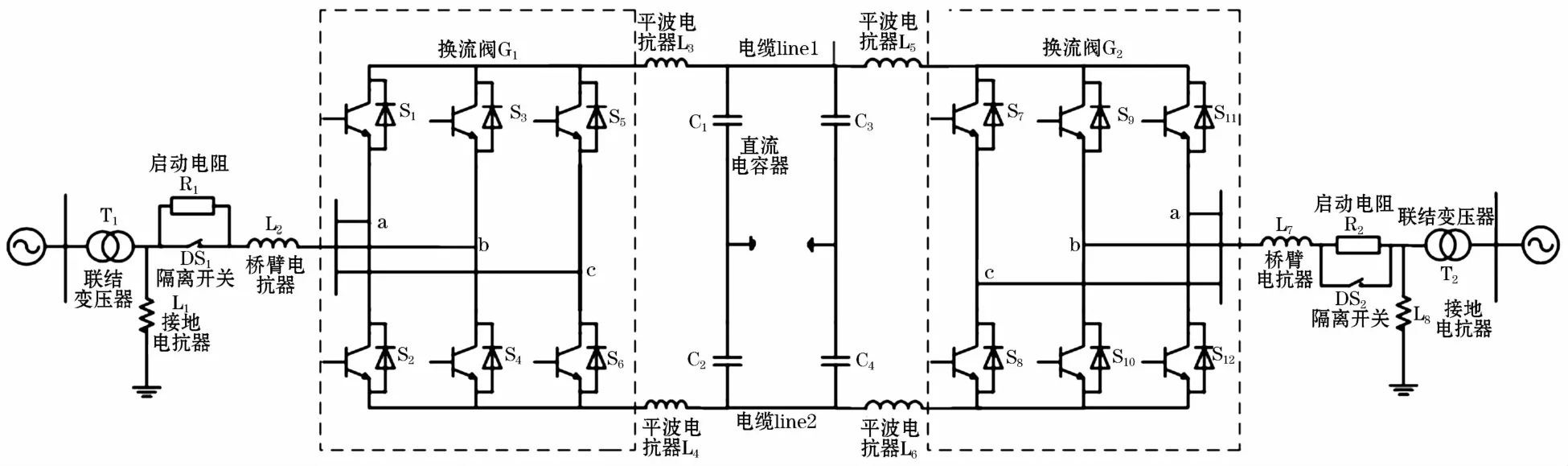
图1 典型柔性直流输电系统拓扑结构Fig.1 Topology diagram of typical flexible HVDC system

2 柔型直流输电系统主要设备能耗分析

将图1简化，可得典型柔性直流输电系统的能耗分析示意图，如图2所示。图中1～8代表单个换流站的计量点，P1～P8代表该计量点处的功率。本节将结合图2中所述元件的数学模型进行能耗分析，包括联接变压器T1、接地电抗器L1、启动电阻R1、桥臂电抗器L2、换流阀G1、平波电抗器L3和电缆line。

图2 典型柔性直流输电系统的能耗分析示意图Fig.2 Power consumption analysis schematic diagram of typical flexible HVDC system

2.1 联接变压器损耗

当不计及谐波电流时，联接变压器T1的有功功率损耗为［8］：

式中P0为空载损耗；β为负载电流与额定电流之比；KT为负载波动损耗系数，一般取0.9～1；Pk为短路损耗。

2.2 接地电抗器损耗

接地电抗器主要为阀侧提供钳制接地电位，故接地电抗器L1的损耗可以表示为：

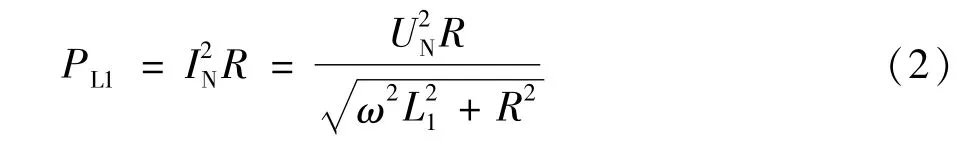
2.3 启动电阻损耗

由于柔直系统换流阀充电回路阻尼较小，启动电阻可以限制启动过程中产生的过电流冲击，但在柔直系统启动后，由隔离开关DS1将启动电阻旁路，因此，在正常运行过程中，启动电阻不产生损耗。

2.4 桥臂电抗器损耗

桥臂电抗器L2的损耗主要包括直流损耗Pd_L2和谐波损耗Ph_L2。直流损耗Pd_L2可表示为：

式中IN为额定电流；R为接地电抗器的等效串联电阻与外接串联电阻之和；UN为连接变压器阀侧额定电压；ω为角频率。

式中IdN为额定直流电流；RL2为包括引线在内的桥臂电抗器的绕组电阻。

谐波损耗Ph可表示为：

式中N为最高谐波次数；Ih为各次谐波电流有效值。

则桥臂电抗器L2总损耗为：

2.5 换流阀损耗

柔性直流输电系统采用模块化多电平换流器（以下称MMC），其拓扑结构如图3所示。其中，L0为桥臂电抗器，SM1、SM2、SMn为 MMC的子模块，每个子模块由上下两个IGBT组成，D1、D2为IGBT自带反并联二极管或外并二极管。

根据对MMC工作状态的分析，可以得到对应开关时刻的相应损耗，如表1所示［1］。

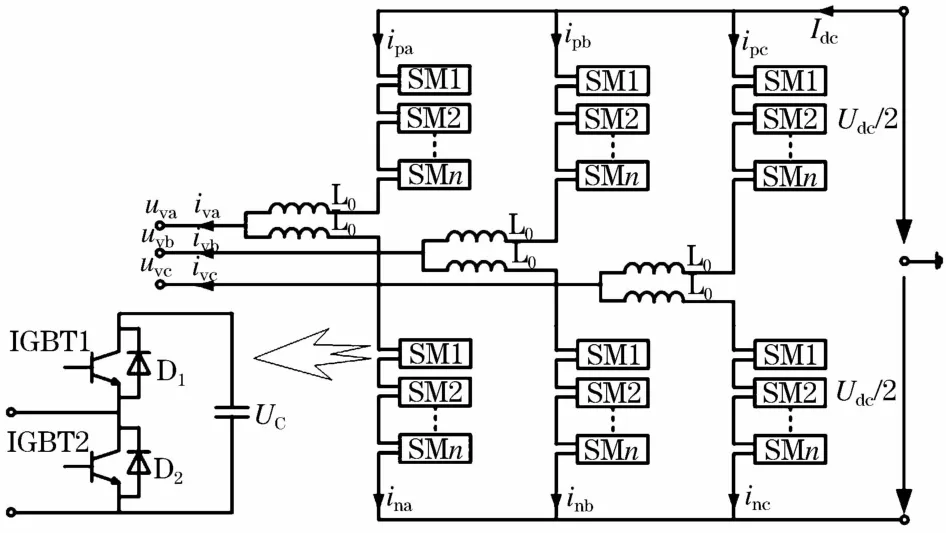
图3 MMC拓扑结构图Fig.3 Topology structure diagram of modular multilevel converter

表1 开关动作及损耗组成Tab.1 Switching and losses composition

换流阀功率损耗主要包括：IGBT和反并二极管的通态损耗、IGBT开通和关断损耗、反并二极管反向恢复损耗。在确定IGBT和二极管的型号后，其损耗主要受到器件正向导通电阻、工作电流、开关频率、结温等因素影响。可通过IGBT和二极管器件厂商提供的相关特性曲线，结合换流器中各器件的工作状态，计算换流器的损耗。

2.5.1 通态损耗

图4所示为IGBT的VCE-IC曲线，其中，VCE为集射极电压，IC为集电极电流，该曲线可以用一次函数式（6）近似拟合：

式中RT和VCE0分别为IGBT正向导通电阻和擎住电压，在结温T1（125℃）和T2（25℃）下，分别得到两组典型参数（RT1-VCE01）和（RT2-VCE02），通过插值，可得到结温Tvj下RT和VCE0的值：

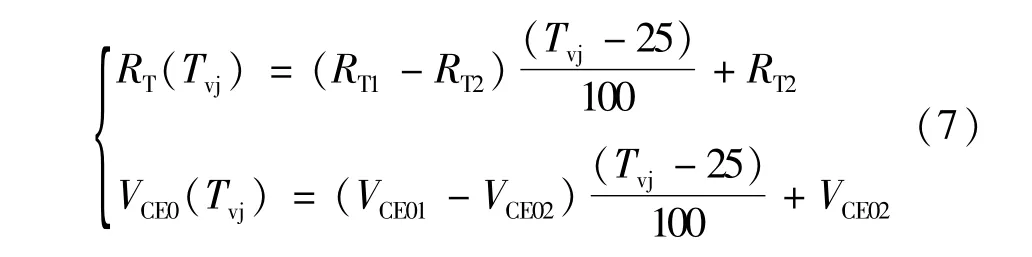
故IGBT通态损耗的功率为：

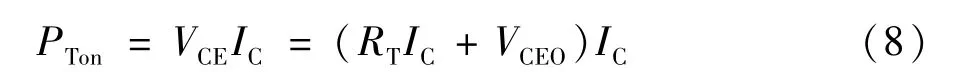
同理，反向并联二极管的通态损耗功率Pcon为：

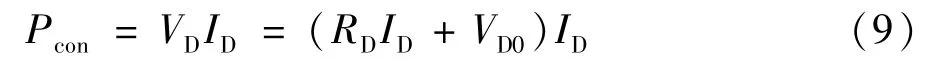
式中VD和ID分别为二极管的工作电压和工作电流；RD和VD0分别为二极管的导通电阻和门槛电压，与结温有关。

由式（8）和式（9）可知，对于选定的IGBT和二极管，工作电流和结温决定了器件的通态损耗。

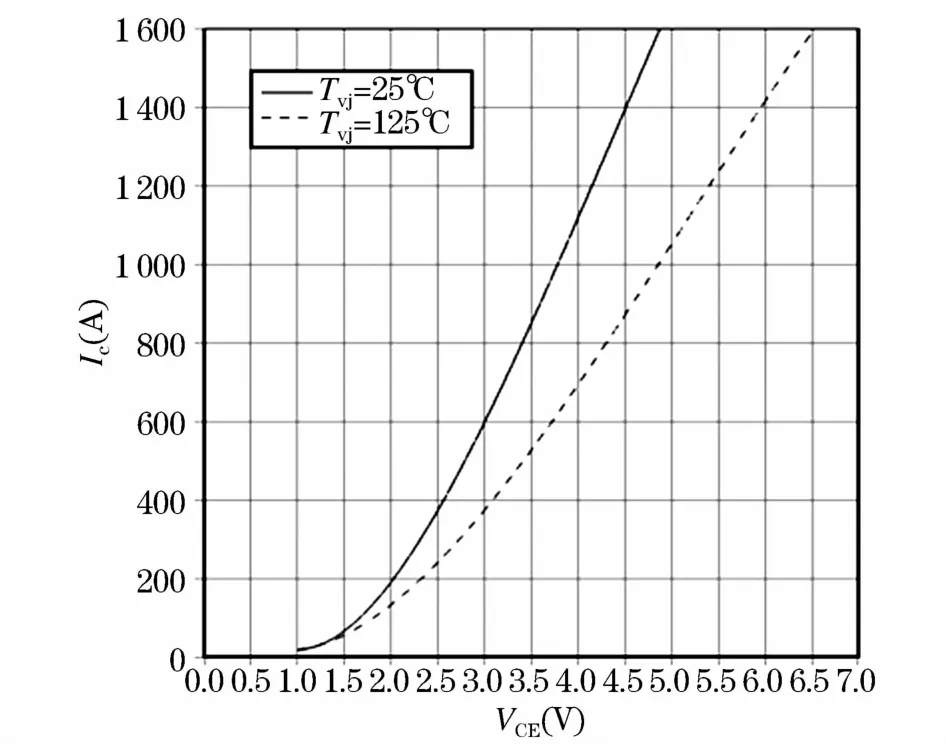
图4 IGBT的VCE-IC曲线Fig.4 The VCE-IC curve of IGBT

2.5.2 开关损耗

IGBT开关损耗Esw和二极管反向恢复损耗Erec为［1］：

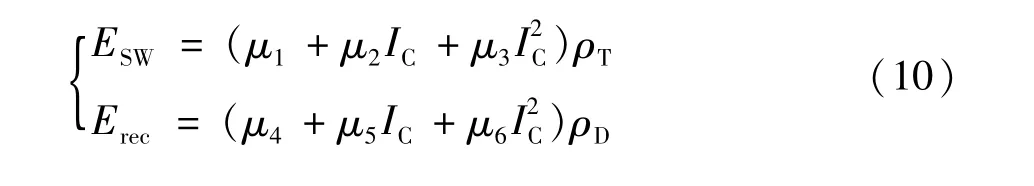
式中ρT和ρD分别为IGBT和二极管的结温系数。参数μ1、μ2、μ3、μ4、μ5、μ6可以利用厂商的EswNIC和ErecN-IC特性曲线来进行参数拟合获得。μ1、μ2、μ3、μ4、μ5、μ6都受结温的影响，满足一定温度范围时，可以利用插值法得到损耗的结温系数，IGBT开关损耗和二极管反向恢复损耗的结温系数表示如下：

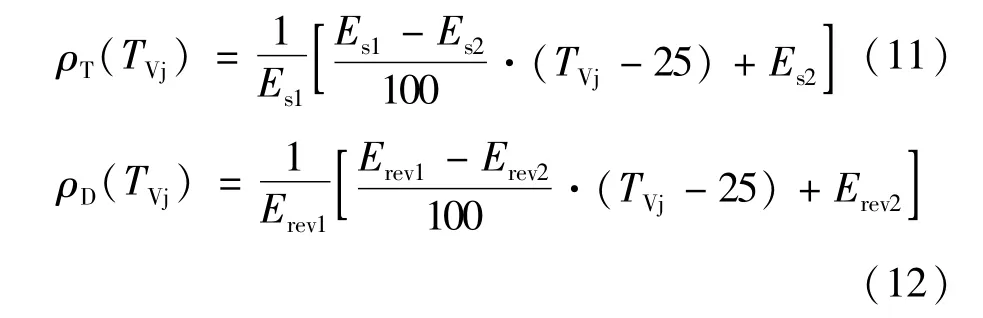
式中Es1、Es2分别为IGBT额定电压、电流下结温125℃和25℃时的开关损耗；Erev1、Erev2为额定电压、电流下125℃和25℃时二极管的反向恢复损耗。因此，假设每个桥臂的总模块数为N，可得换流阀的总损耗为：

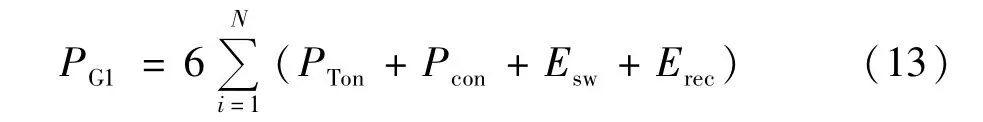
2.6 平波电抗器损耗

平波电抗器的实际损耗与其运行环境和运行参数有关［9-10］。平波电抗器L3的损耗主要包括直流损耗Pd_L3、谐波损耗Ph_L3、铁芯损耗Pm_L3：

直流损耗Pd_L3为：

式中IdN为额定直流电流；RL3为包括引线在内的平波电抗器的绕组电阻。

谐波损耗Ph_L3为：

式中N为估算的最高谐波次数；Ih为各次谐波电流有效值。

铁芯损耗Pm_L3为：

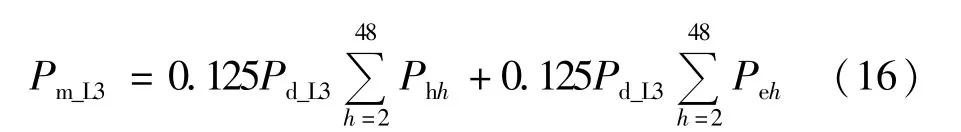
式中Phh为磁滞损耗；Peh为涡流损耗。

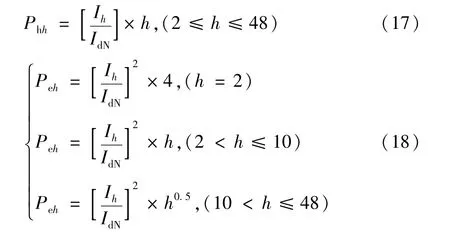
则平波电抗器损耗PL3为：

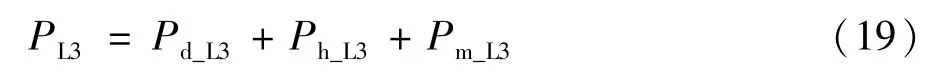
2.7 电缆损耗

直流电缆的损耗主要由其等效电阻发热造成，且直流输电电流中的纹波电流通常较小，由其引起的损耗可忽略不计［10］，则电缆中的损耗可表示为：

式中l为电缆的线路长度；I为直流电流；R为等效电阻。

2.8 典型算例

舟山柔性直流输电系统额定直流电压为±200 kV，额定直流功率为400 MW，桥臂子模块数目为250，额定调制比为0.85；模块化多电平换流器子模块采用的型号是EUPEC FZ800R33KF2C；联接变压器短路损耗900 kW，空载损耗150 kW；接地装置中接地电抗器的电感值为3H，额定电流为12.6 A，接地电阻值为1 000Ω，额定电流为12.6 A；桥臂电抗器额定直流电流分量为333 A，额定交流分量为633 A，电感值为90 mH；平波电抗器的额定直流电流为1 000 A，电感值为20 mH；电缆的长度为52 km，单位长度电阻值为0.017 6Ω/km。结合舟山柔性直流输电系统实际工程，根据上述损耗计算方法，得到如下计算结果，如表2所示。

表2 舟山柔性直流输电系统满载情况下的损耗分布情况Tab.2 Loss distribution of Zhoushan flexible HVDC system under full load conditions

从表2可以看出舟山柔性直流输电系统中主要能耗来源为换流阀与联结变压器，占总损耗的86.3%左右；接地电抗器、桥臂电抗器、平波电抗器以及电缆损耗所占的比例相对较低。

同时，为了较为直观地显示柔性直流输电系统在升功率过程中输送功率与损耗率的关系，将有功功率作为自变量，系统的损耗率作为因变量绘制曲线图，如图5所示。

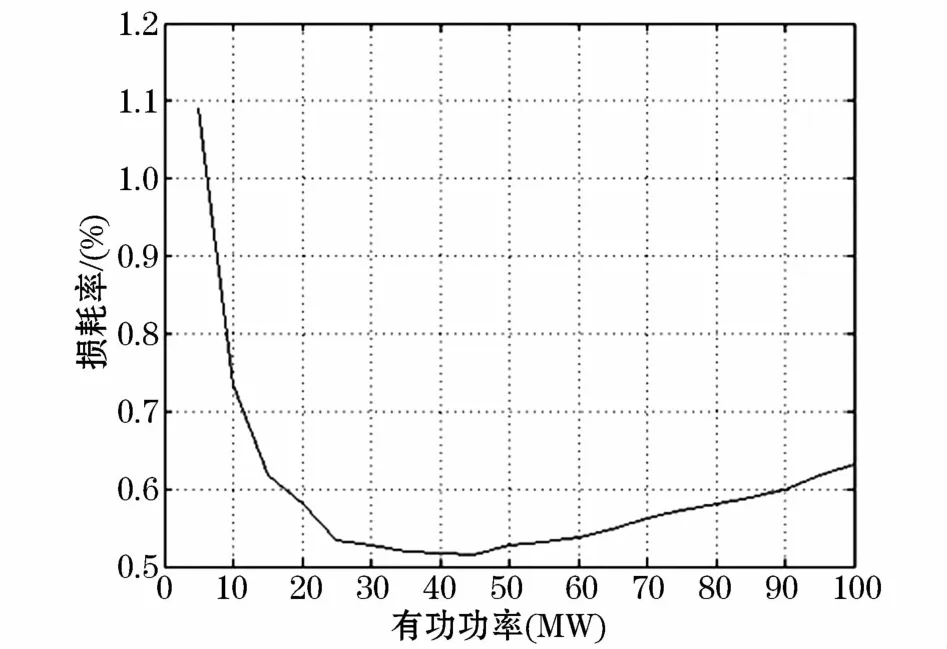
图5 系统总损耗率与传输功率的关系图Fig.5 Relationship diagram of loss rate and transmission power

由图5可知，随着传输功率的增加，系统损耗率呈现先降低后增加的趋势。

3 柔性直流输电系统能效计量点设置

柔性直流输电系统能效计量点的设置主要考虑以下几方面的因素：

（1）经济性

根据前述的柔性直流输电系统设备损耗分析可知，换流阀和联接变压器损耗占比通常在80%以上。考虑到经济成本，无法在所有设备能量输入输出两端加装计量装置时，应将计量装置安装在损耗较大的元件两侧。另一方面，对运行方式相对固定、损耗较小的元件，如电抗器、电缆等元件，可根据相关特性通过数学分析获得较为精确的损耗；

（2）谐波影响

柔性直流输电系统计量点的选择应考虑系统谐波特性。当换流器的电平数目较大时，一般选用最近电平逼近调制（Nearest Level Modulation，NLM）控制。NLM方法的换流器端口的相电压主要包含低频奇次谐波，但对于三相对称系统，各相电压中3倍频谐波的相位相同，可在线电压中相互抵消。因此对于三相对称的系统，NLM方法的线电压特征谐波只有6k±1次谐波；

在电平数目较小时，各次特征谐波含量均比较大；随着电平数目的提高，各次谐波含量明显降低。51电平阶梯波的各次谐波含量在0.4%以下［1］。从谐波特性可以看出，图2中的计量点4经过和计量点7谐波较小。

（3）计量点设置

综合考虑经济性、谐波影响等因素，可知：

1）由于正常运行时启动电阻被开关旁路，因此计量点1、2、4的计量数据可以得到联接变压器和接地电抗器的总损耗；

2）计量点5位于桥臂电抗器后，若在此设置计量点，则需要在A、B、C三相共6个桥臂上加装电流互感器与电压互感器等计量装置，成本较高，且此处谐波含量高，不易准确计量。同时由表2可知，桥臂电抗器损耗占比不高，因此选择不在5处设置计量点；

3）由表2可知，平波电抗器损耗占比较小且容易准确计算，加之计量点7谐波含量小，因此选择在计量点7开展计量；

4）计量点8实际是对侧换流站中的计量点7。

根据上述分析，提出柔性直流输电系统能效计量分别在1、2、4、7等节点加装电能计量装置。本方案的缺点在于受到实际安装情况的限制，不能区分出平波电抗器、桥臂电抗器和换流阀各自的损耗。但可由理论分析，分别计算这三部分的损耗，结合实际数据和仿真数据，可确定平波电抗器、桥臂电抗器和换流阀各自的损耗。

4 能效计量器具准确度等级

能效计量除了计量装置的准确度等级外，还应该考虑相关联计量点所配置的计量装置的误差一致性。

在图2中，桥臂电抗器L2、换流阀G1和平波电抗器L3的电能总损耗ΔPz可表示为：

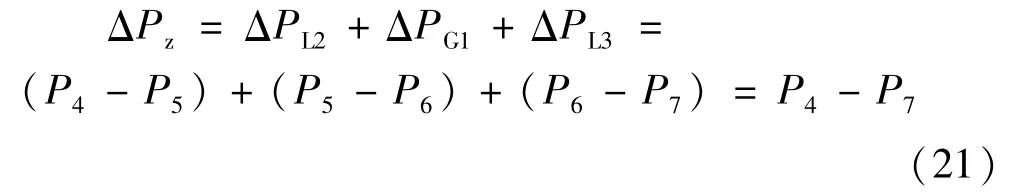
式中P4、P5、P6、P7分别为图2计量点 4、5、6、7处的功率，则由于计量点4、7处计量器具的误差，使得ΔPz产生的计算误差等于：

式中 Δ（ΔPz）为 ΔPz的误差；ΔP4和 ΔP7分别为计量点4和计量点7处电能计量装置的误差。

根据表2的典型算例分析，桥臂电抗器、换流器和平波电抗器的电能总损耗约占总功率P的0.658%，此处按 ΔPz≈0.66%P。且有P4≈P、P7≈P，则：

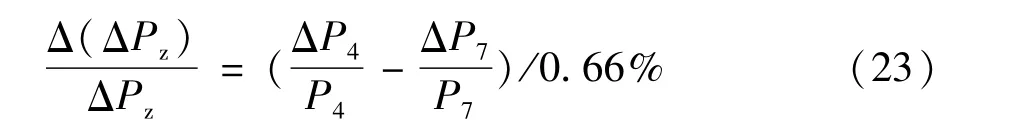
用Y4，7=（ΔP4/P4）-（ΔP7/P7）表示计量点4和计量点7处电能计量装置的一致性，电能损耗ΔPz的相对误差与Y4，7的关系如表3所示。

表3 ΔPz的相对误差与 Y4，7的关系Tab.3 Relationship between the relative error ofΔPz and Y4，7

由表3可知，电能计量装置误差一致性程度越高，能效计量相对误差越小。考虑到现有计量装置准确度等级，能效计量点应配置0.2S级电流互感器、0.2级电压互感器以及有功准确度等级为0.2S级的电能表，且相应能效计量点电能计量装置误差一致性应优于0.05%，使能效计量相对误差最小化；同时，考虑到柔性直流输电系统可以进行双向的电能传输，应配置具有正反向计量功能的电能表。

5 结束语

本文定量分析了柔性直流输电系统的能效计量方案，主要结论有以下三点：

（1）在柔性直流输电系统中，换流阀和联接变压器损耗占总损耗的86%左右；

（2）设置联接变压器的输入端、站用变端，桥臂电抗器前端，和电缆输入输出端为能效计量点，加装电能计量装置；

（3）考虑到现有计量装置准确度等级，应配置0.2S级电流互感器、0.2级电压互感器以及有功准确度等级为0.2S级的电能表且相应能效计量点电能计量装置误差一致性应优于0.05%。