台阶地形爆破振动放大与衰减效应研究*
武 旭,张云鹏,郭奇峰
台阶地形爆破振动放大与衰减效应研究*
武 旭1,2,张云鹏3,郭奇峰1,2
(1.北京科技大学土木与资源工程学院,北京100083;2.北京科技大学金属矿山高效开采与安全教育部重点实验室,北京100083;3.华北理工大学矿业工程学院,河北 唐山063009)
基于台阶地形爆破振动数值模拟与边坡振动监测实验,研究台阶地形爆破振动速度在传播过程中高程放大效应的产生及变化规律。结果表明,单个台阶坡顶质点的振动速度放大效应是在距爆源一定距离、达到一定高差的条件下产生的;坡顶质点振动速度放大倍数并不随台阶高度的增加而单调增加,在台阶高度超过某一临界值后,放大倍数随台阶高度的增加而减小。台阶高程对爆破振动速度既有放大作用,同时也随高度的增加产生衰减作用。根据模拟计算及现场观测数据分析结果,给出了台阶地形爆破振动速度预测模型,该模型为类似边坡工程的爆破地震波传播规律研究提供一定的参考。
台阶地形;高程差;爆破振动;放大效应
爆破振动强度的影响因素极其复杂,其衰减特征是在基于实践经验和对数据统计分析的基础上得到的,随着爆破技术在边坡工程中的广泛应用,萨道夫斯基公式计算值与实测数据的误差达到50%以上[1],该公式对高差变化较大的地形已不再适用。许多学者采用现场实验、理论分析及数值模拟等手段对爆破振动的地形效应进行了深入研究。台阶地形的放大效应与高程、爆源距、坡面角以及结构面的产状有关[2-5]。吕淑然等[6]认为台阶正高差地形的高程越高放大效应越明显,而唐海等[1]认为台阶地形中振动速度的放大系数存在最大值。万鹏鹏等[7]通过实验观测分析得到台阶地形爆破振动放大效应是受鞭梢效应和坡面效应影响的结论。张伟康等[8]、胡光球等[9]、周同龄等[10]通过分析与爆破振动有关的物理量,运用量纲分析法推导了反映高程放大效应的爆破振动公式并在工程中应用。同时,动力有限元方法成功应用在了爆破动态模拟中,并被证明在边坡顶部质点振动速度都呈现出放大效应[11],放大现象是一个局部的动力响应[12],振动速度放大效应的实质是在台阶平台上产生波形转换及波形叠加[13]。
本文中利用数值模拟方法对台阶地形爆破地震波的放大与衰减规律进行研究,结合现场实验数据分析结果提出台阶地形爆破振动速度预测模型。
1 数值模拟
1.1 参数选取
模型做如下假设:岩石视为各向同性的连续均匀介质,爆轰产物的膨胀是绝热过程;忽略重力影响。台阶模型的岩石材料参数如表1所示,炸药材料及状态方程参数如表2所示。

表1 岩石材料参数Table 1Material parameters of rock

表2 炸药的材料和状态方程参数Table 2Material and equation of state parameters of explosive
采用高能炸药材料和JWL状态方程描述,爆轰压力计算:
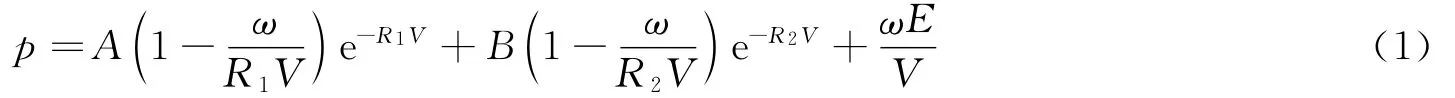
式中:p为爆轰压力,E为炸药爆轰产物的内能,V 为爆轰产物的相对体积,A、B、R1、R2、ω、为所选炸药的性质常数。
1.2 模型建立
利用LS-DYNA程序建立爆破模型,根据实验方案、岩石物理力学参数以及爆破参数,边坡爆破各模型尺寸:台阶高度H 分别为12、15、18、21m;台阶坡底面宽度W 分别为10、15、20m;坡面角为90°。图1中给出了模型边界条件及炮孔主要参数。
1.3 台阶高度对振速的影响
模型计算时间0.03s。爆炸后模型质点竖直方向振动速度随时间变化形态如图2所示。
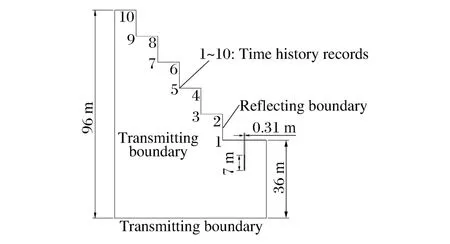
图1 计算模型示意图Fig.1Sketch map of calculation model

图2 振动速度云图Fig.2Vibration velocity nephogram
通过LS-PrePost后处理程序提取时间历程记录点处竖直方向的峰值质点振动速度,12组数值模型的计算结果如图3所示。
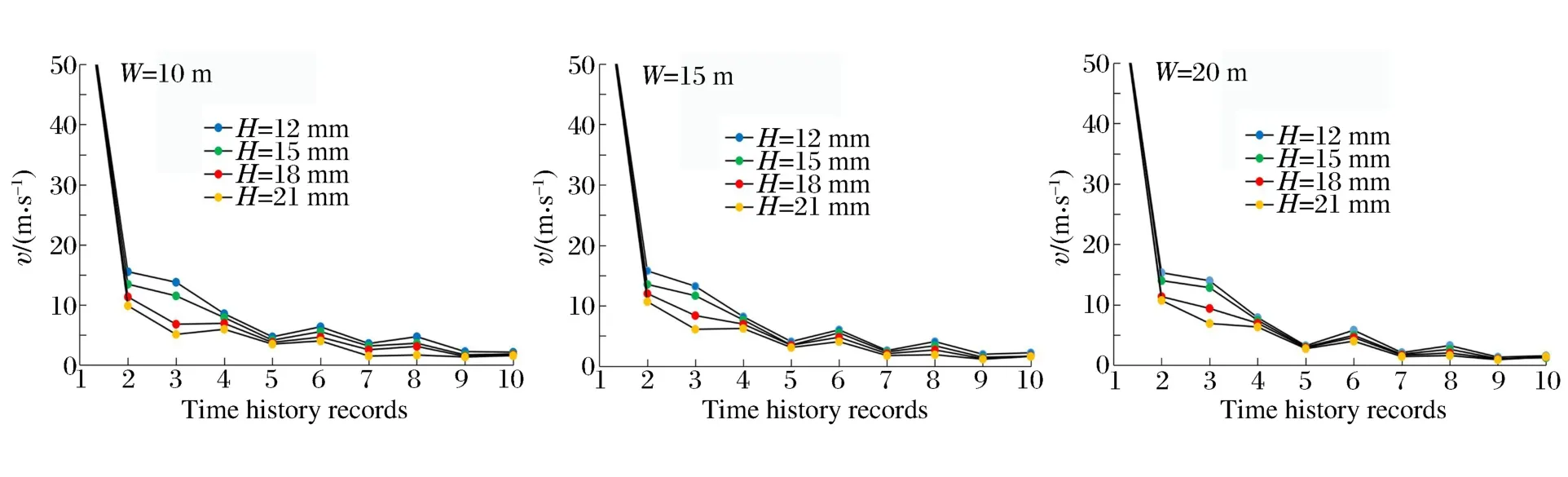
图3 质点峰值振动速度随高程变化曲线Fig.3Variation of peak particle vibration velocity with elevation
台阶表面质点振动速度总体上随距离的增加呈指数衰减规律;对于单个台阶,由于高差的存在质点振动速度在上级台阶坡顶处产生放大效应。由图2中曲线分析可得:爆破振动速度的高程放大效应是在爆源距和高差达到一定值后产生。当W=10m、H=12m,振动速度的放大效应在第3级台阶出现,为研究产生放大效应后高程对振动速度的影响规律,改变第3级台阶的高度,建立16个台阶模型。
台阶坡顶质点振动速度的放大倍数n随高差的变化曲线如图4所示,高差由1m增加到18m,放大倍数n呈现先增加后降低的变化规律,当高差为9m时,放大倍数n达到最大值1.34。
质点振动速度的放大倍数并不随台阶高度的增加而单调增加,当台阶高度超过某一临界值时,放大倍数随台阶高度的增加而减小。这一现象表明,高程对地震波既有放大作用也存在衰减作用。

图4 放大倍数随高程变化曲线Fig.4Variation of amplification factor with elevation
1.4 台阶坡底面宽度对振速的影响
当台阶高度一定,坡底面宽度分别为10、15、20m时,建立12组数值模型,台阶坡顶、坡底处质点峰值振动速度与坡底面宽度的关系如图5所示。
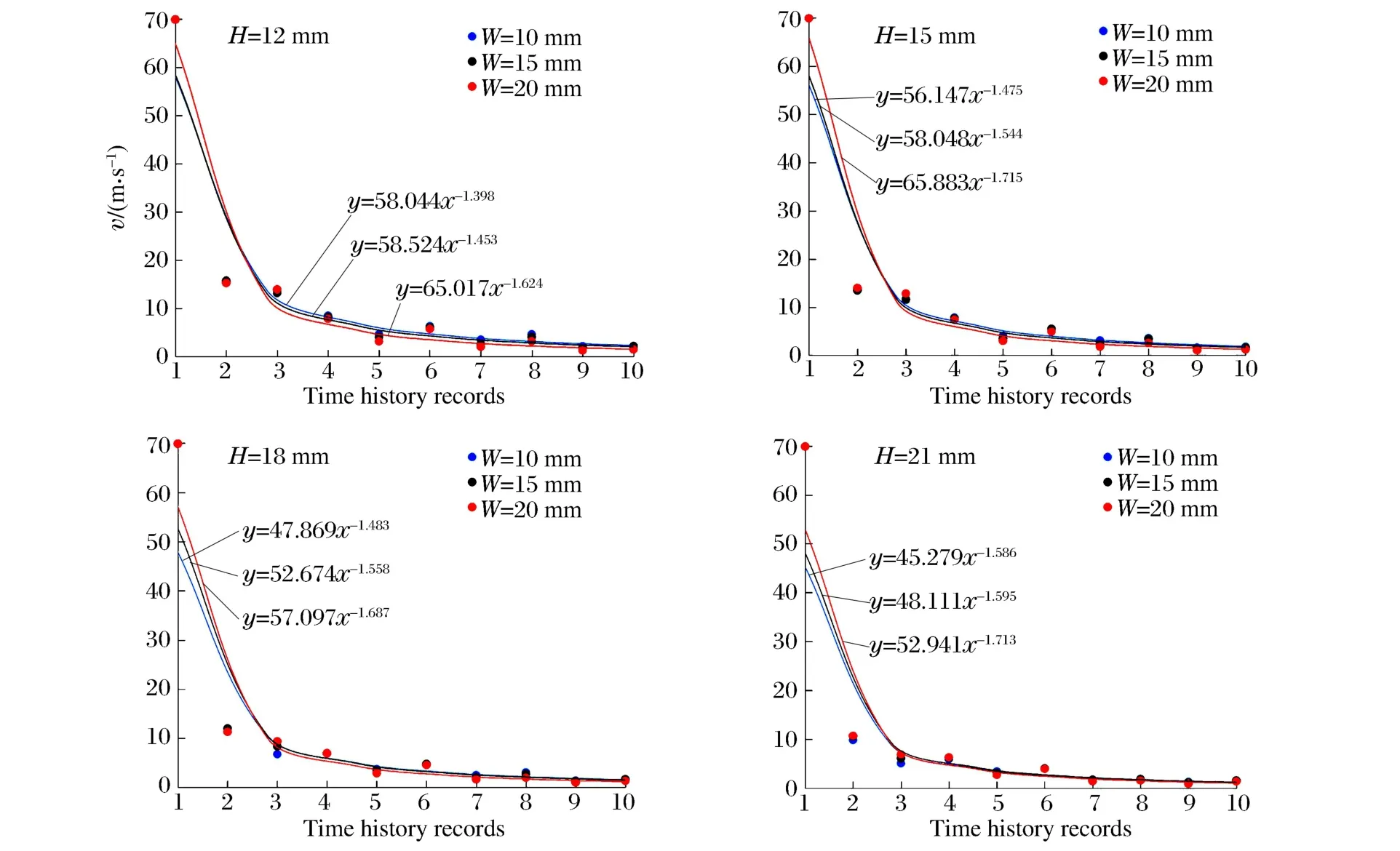
图5振动速度与坡底面宽度的关系Fig.5Relation of bottom width with vibration velocity
图4 中质点峰值振动速度衰减特征显示,坡底面宽度越大,相同高程处质点振动速度越低;坡底面宽度较大台阶的爆破振动速度衰减速率更快。振动速度随坡面宽度增大而减小。在有高差存在的台阶地形中,高程和爆源水平距离的共同作用影响爆破振动速度的大小。
2 反应高程的数学模型
根据模拟实验数据的分析结果,结合对各参考文献中爆破振动速度计算经验公式的分析,认为用下式对台阶地形爆破振动速度计算更为准确:

式中:v为质点峰值振动速度,Q为装药量,R为距爆源的水平距离,H 为高程差,K、α、β为与岩石、地形相关的系数。

图6 高程对振速的放大与衰减示意图Fig.6Amplification and attenuation of vibration velocity based on elevation
如图6所示,炸药爆炸后产生的爆破地震波传播至点A、B、C时,水平距离R对振动速度的衰减作用相同,A点振动速度为v,由于高程的影响B点振速为v+v′,高差h1对振动速度起到放大作用;当单个台阶高程增加为h1+h2时,C点速度降为v-v″,此时高程对振动速度起到衰减的作用。式(2)中R为距爆源水平距离,不影响高差对振速的作用。高差H 值在一定范围内,产生振速放大效应,数据拟合得到的β为负值;高程增加到某一值后,此时速度v随着H 的不断增加而降低,数据拟合得到的β为正值。
3 工程实例
露天深孔爆破炮孔直径310mm,孔深14~17.5m,超深2~2.5m,填塞长度7~8m,孔网参数:矿石a×b=(7~8)m×(6~7)m,岩石a×b=(5~9)m×(4~8)m。露天台阶高度12~15m。
爆破振动监测工作采用TC-4850爆破测振仪,如图7所示。布置8个测点采集各台阶坡底和坡顶质点振动速度,测点位置如图8所示。

图7 爆破振动速度现场监测Fig.7Field monitoring of blasting vibration velocity

图8 测点布置台阶剖面图Fig.8Arrangement of measuring points

表3 爆破振动观测结果Table 3Blasting vibration measurements
从表3数据可知,测点4、6和8均出现振动速度放大现象,根据公式(2)进行数据拟合处理得:

相关系数r2=0.995 3;撒道夫斯基公式拟合相关系数为0.945 3,相关性与公式(2)相比较低,且不能直观体现地形高差对爆破振动速度的影响。
4 结 论
(1)台阶表面质点振动速度随着距离的增加整体上呈指数衰减规律;对于单个台阶,由于高差的存在坡顶质点产生振动速度放大效应,放大效应在距爆源一定距离、达到一定高差的条件下产生。
(2)坡顶质点振动速度放大倍数并不随台阶高度的增加而单调增加,台阶高度超过某一临界值后,放大倍数随台阶高度的增加而减小。
(3)坡底面宽度越大,爆破振动速度衰减速率越快,相同高程处质点振动速度越小。
[1] 唐海,李海波.反映高程放大效应的爆破振动公式研究[J].岩土力学,2011,32(3):820-824.Tang Hai,Li Haibo.Study of blasting vibration formula of reflecting amplification effect on elevation[J].Rock and Soil Mechanics,2011,32(3):820-824.
[2] 朱传统,刘宏根.地震波参数沿边坡坡面传播规律公式选择[J].爆破,1988,5(2):30-34.Zhu Chuantong,Liu Honggen.Selection of formula on propagation of the parameters of explosive seismic wave along slope[J].Blasting,1988,5(2):30-34.
[3] 王在泉,陆文兴.高边坡爆破开挖震动传播规律及质量控制[J].爆破,1994,11(3):1-4.Wang Zaiquan,Lu Wenxing.Propagation of blasting vibration and quality control of high slope in excavation by blast[J].Blasting,1994,11(3):1-4.
[4] 舒大强,何蕴龙,董振华.岩质高边坡开挖爆破震动荷载及其对边坡稳定性影响的研究[J].工程爆破,1996,2(4):39-43.Shu Daqiang,He Yunlong,Dong Zhenhua.Research on vibration load from excavation blasting and its influence on stability of rock high-slope[J].Engineering Blasting,1996,2(4):39-43.
[5] 舒大强,李小联,占学军,等.龙滩水电工程右岸高边坡开挖爆破震动观测与分析[J].爆破,2002,19(4):65-67.Shu Daqiang,Li Xiaolian,Zhan Xuejun,et al.Observation and analysis of blasting vibration on the right bank’s high slope of Longtan hydropower project[J].Blasting,2002,19(4):65-67.
[6] 吕淑然,杨军.露天矿爆破地震效应与降震技术研究[J].有色金属,2003,55(3):30-32.LüShuran,Yang Jun.Study on blasting seismic effect and anti-vibration technology in the open-pit mine[J].Non-ferrous Metal,2003,55(3):30-32.
[7] 万鹏鹏,璩世杰,许文耀,等.台阶爆破质点振速的高程效应研究[J].爆破,2015,32(2):29-32.Wan Pengpeng,Qu Shijie,Xu Wenyao,et al.Study of elevation effect of bench blasting particle vibration velocity[J].Blasting,2015,32(2):29-32.
[8] 张伟康,谢永生,吴顺川,等.矿山边坡爆破振动高程放大效应研究[J].金属矿山,2015,44(3):68-71.Zhang Weikang,Xie Yongsheng,Wu Shunchuan,et al.Research on elevation amplification effect of blasting vibration in mine slope[J].Metal Mine,2015,44(3):68-71.
[9] 胡光球,璩世杰,梁新民.高程放大效应对露天采场爆破震动衰减的影响研究[J].黄金,2015,36(7):28-32.Hu Guangqiu,Qu Shijie,Liang Xinmin.Research on the influence of elevation amplification effect on open-pit blasting vibration attenuation[J].Gold,2015,36(7):28-32.
[10] 周同龄,李玉寿.反映高程的爆破震动公式及其应用[J].江苏煤炭,1997,22(4):21-22.Zhou Tongling,Li Yushou.Blasting vibration formula of reflecting amplification and application[J].Jiangsu Coal,1997,22(4):21-22.
[11] 付波,胡英国,卢文波,等.岩石高边坡爆破振动局部放大效应分析[J].爆破,2014,31(2):1-7.Fu Bo,Hu Yingguo,Lu Wenbo,et al.Local amplification effect of blasting vibration in high rock slope[J].Blasting,2014,31(2):1-7.
[12] 林士炎,李长洪,乔兰,等.爆破震动对高速路边坡影响的数值模拟[J].北京科技大学学报,2003,25(6):507-509.Lin Shiyan,Li Changhong,Qiao Lan,et al.Numerical simulation on the influence of blasting vibration on the freeway slope[J].Journal of University of Science and Technology Beijing,2003,25(6):507-509.
[13] 李山有,马强,韦庆海.地震体波斜入射下的断层台阶地震反应分析[J].地震研究,2005,28(3):277-281.Li Shanyou,Ma Qiang,Wei Qinghai.Seismic response analysis of fault step subjected to obliquely incident body waves[J].Journal of Seismological Research,2005,28(3):277-281.
Amplification and attenuation effect of blasting vibration on step topography
Wu Xu1,2,Zhang Yunpeng3,Guo Qifeng1,2
(1.School of Civil and Environmental Engineering,University of Science and Technology Beijing,Beijing100083,China;2.Key Laboratory of High-Efficient Mining and Safety of Metal Mines,University of Science and Technology Beijing,Beijing100083,China;3.College of Mining Engineering,North China University of Science and Technology,Tangshan 063009,Hebei,China)
The present study investigates the growth and variation of the amplification effect in the propagation of the blasting vibration velocity in step topography.The results indicate that the blast vibration elevation amplification effect on a single step occurs at a certain distance and elevation;the peak particle velocity magnification of the top of the slope doesn’t increase monotonously with the increase of the elevation;and the magnification decreases when the elevation exceeds a certain critical value.The elevation exerts an effect of both amplification and attenuation on the blasting vibration velocity.According to the data analysis of the numerical simulation and the field experiment,a model of the blasting vibration velocity prediction on step topography was presented,providing reference for the research of blasting seismic wave propagation law in similar slope projects.
step topography;elevation difference;blasting vibration;amplification effect
O389 国标学科代码:13035
A
10.11883/1001-1455(2017)06-1017-06
2016-03-29;
2016-07-29
国家自然科学基金项目(51604017);中央高校基本科研业务费专项基金项目(FRF-TP-16-017A3)
武 旭(1988— ),男,博士,13051510807@163.com。
(责任编辑 曾月蓉)

