数字化变电站采样值报文非整周期采样误差分析及其补偿算法研究

段太钢，吴双惠，金华蓉，卜银娜，寇华垒

（许继电气股份有限公司，河南 许昌 461000）

0 引 言

数字化变电站是近年来高速发展的新兴技术，是未来电网技术的发展趋势。采样值报文在数字化变电站中占据非常重要的地位。过程层电子互感器采集电流电压信号后，通过光纤将采样值报文传输给间隔层及站控层设备。目前，国际电工委员会（IEC）已经制定了电子式电压互感器标准 GB／T 20840.7-2007［1］和电子式电流互感器标准 GB／T 20840.8-2007［2］，对基于光纤串口的采样值报文传输进行了规范。SAC／TC 57制定了 DL／T 860.91［3］和DL／T 860.92［4］标准，对基于光纤网口的采样值报文传输进行了规范。这些标准有利于实现变电站综合自动化系统的标准化和互操作性。

限于智能设备的处理能力和网络设备的吞吐能力，IEC 61850规定的采样值报文采样率较低。有每周波40点、80点、160点、256点等速率，一般采用每周波80点。相对于传统电量信号每周波1 000点以上的采样率非常低。显然，在低采样率的情况下，非整周期采样问题更为明显，直接导致傅里叶变换的频谱泄露现象和栅栏效应更为严重［5］。这都将严重影响频域分析的准确度，特别是对相位精度的影响很大。

现有方法大多是通过加窗插值傅里叶变换减小这种误差［6-10］，只考虑了频率偏差对结果的影响。实际上，从不同的相位开始截取数据分析，对结果的影响也是不一样的。文献［11］从有效值和功率的角度考虑了初始相位的影响，但是在某些应用场合，需要用傅里叶分析各次谐波含量，有效值和基波含量仍有一定区别。本文从频率和相位两个角度，全面分析傅里叶变换非整周期采样误差，找出误差最小条件，并给出相应补偿算法，提高分析精度。

1 非整周期采样误差分析

实际现场工作条件下，电网频率必定在一定范围内波动，非整周期采样不可避免。以每周波80点为例，IEC 61850采样值报文采样间隔固定为250 μs，不会跟随电网频率变换。因而，在电网频率出现波动的时候，必然出现非整周期采样现象。电网频率可以通过各种频率跟踪算法得到，不在本文讨论范围内，以下分析假设实际电网频率已知。

假设实际电网频率为f，傅里叶分析理论基波频率为F，记λ＝f／F；基波采样点数为N，幅值为Am，初始相位为θ的采样信号时域表达式为：

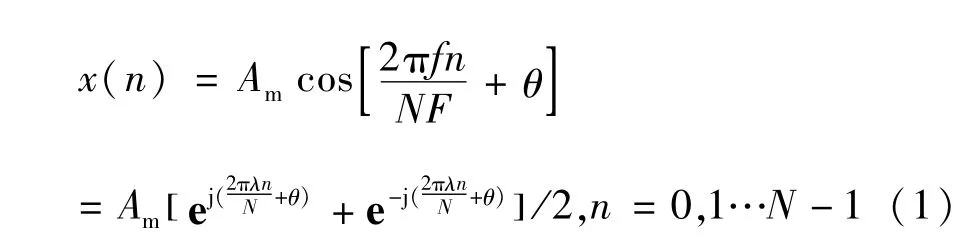
采用离散傅里叶变化（DFT）对采样信号进行频域分析，其DFT的基波分析结果为：

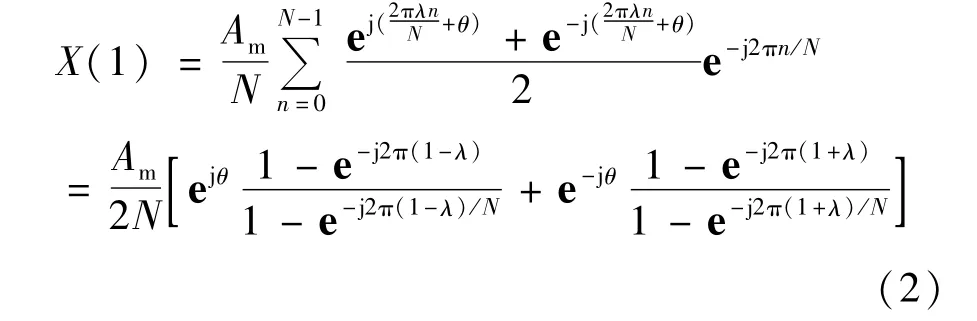
将θ1和θ2记作公式（3）中内容：

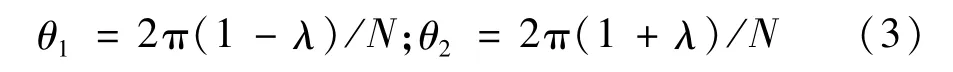
简化公式（2）为：

根据向量误差定义，非整周期采样相对于整周期采样的误差E为：

相量E的幅值即为幅值比差，相量E的相位即为相位误差。根据公式（4）～公式（6）得到误差E表达式为：

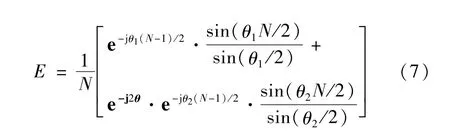
由此可见，非整周期采样误差跟基波采样点数N，频率偏差λ，截取波形初始相位θ有关。而采样点数和频率偏差往往由现场条件决定，后端分析唯一能减少误差的方法是，选取合适的初始相位θ截取数据进行分析。

2 幅值和相位最小误差条件及补偿

在非整周期采样误差分析的基础上，分别从幅值误差和相位误差两个方面寻找最合适的初始相位。

2.1 幅值误差最小条件及补偿

假设，a和b分别定为式（8）中的量：

得到公式（6）向量的模：

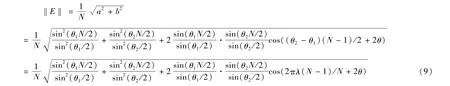
当‖E‖＝1时，幅值误差为0。从式（9）解得幅 值误差最小条件为：

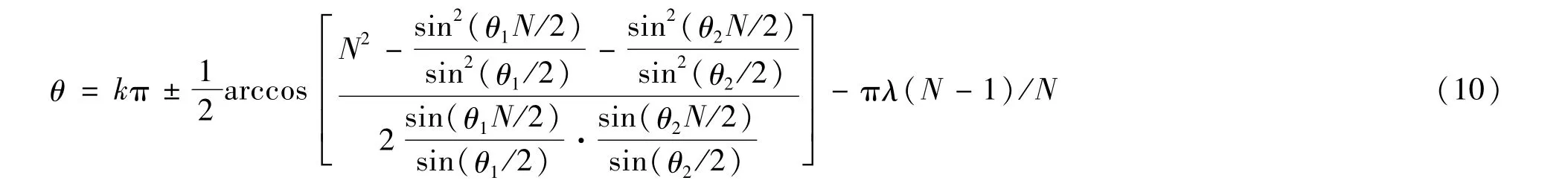
式中k为整数。

因此，当初始相位θ按照式（10）取值时，没有幅值误差。但是在实际应用中，往往不能完全准确取到任意初始相位，应尽量接近最小误差条件取值，然后用式（9）进行补偿。

2.2 相位误差最小条件及补偿

相位误差即为式（6）的向量角度。相位误差角度记为δ，则得到δ：

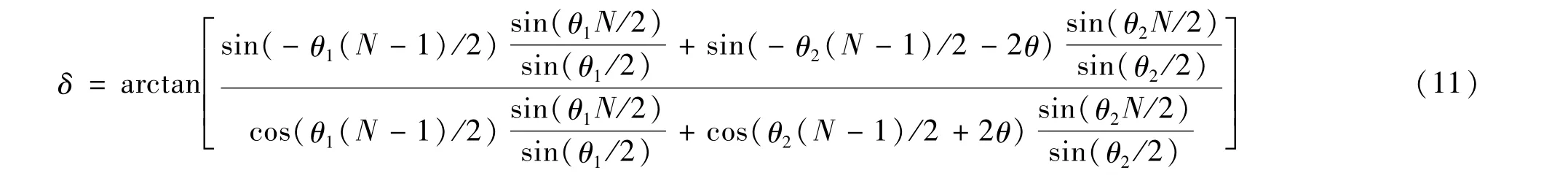
将a，b，α，β分别定义为：

则式（11）简化为式（13）：

寻找最小相位误差条件转化为求函数的极值点，记为f（β）：

式中a，b，α均为已知量，可以通过式（12）求得，β为关于θ的变量。函数f（β）的极值点，必然其一阶导数为0，得到：

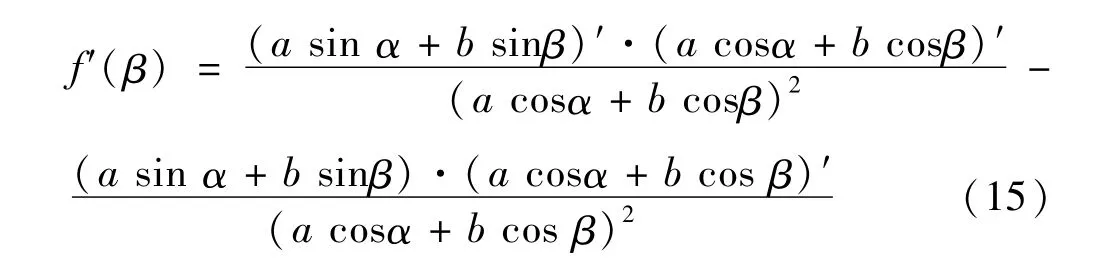
化简式（15），得到：

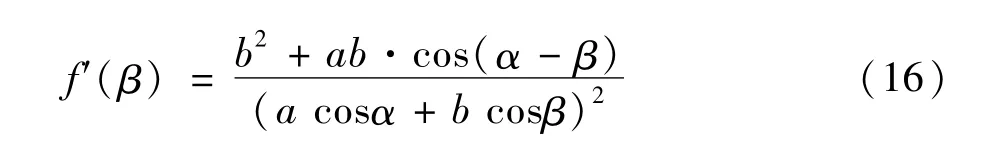
取f′（β）＝0，可以得到：

将式（12）带入式（17），得到：

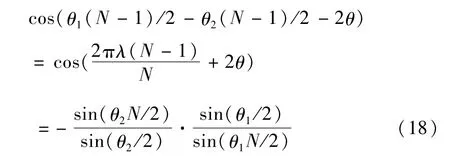
从而得到最小相位误差条件：

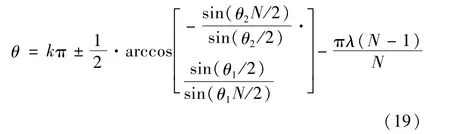
式中k为整数。

在实际应用中，可根据式（19）选取合适的初始相位θ，使相位误差最小。但此时相位误差并不为0，应再根据式（11）进行补偿。

3 软件设计

3.1 最优起始相位角

根据GB／T 15945-1995规定，电网频率允许在［49.8，50.2］Hz范围内波动。本文考虑到故障发生情况下，电网频率波动范围会超过国标规定。因此在实际频率为［49，51］Hz的宽范围内进行仿真，以增强算法的适应能力。

为了验证本文理论分析的正确性。使用基本DFT变换扫描在不同采样点数、不同电网实际频率、不同起始相位角的基波分量幅值误差和相位误差。同时，使用本文算法直接计算在各种情况下的幅值误差和相位误差。两种方法算出的误差完全相同。因此，在表1～表4中，均只提供一种算法的仿真结果。

频率在［49，50］Hz的范围内变化，幅值误差最小时的最优起始相位角如表1所示。

频率在［50，51］Hz的范围内变化，幅值误差最小时的最优起始相位角如表2所示。

表1～表2为从幅值误差角度考虑，在不同采样点数和实际频率情况下的最优起始相位角。从表中数据得出：在实际频率和理论频率均为50 Hz时，从任意起始相位角开始采样，均没有相位误差。幅值误差最小时，最优起始相位角大致在45°附近。随着实际频率的增加，最优起始相位角略微变小；随着采样点数的增加，最优起始相位角也略微变小。本文给出的为IEC 61850规定的采样值报文主要采样点数下的仿真数据。其他采样点数情况下，分析方法完全相同。

表1 频率49.0 Hz～50.0 Hz，幅值误差最小时的最优起始相位角Tab.1 Frequency 49.0 Hz～50.0 Hz，the optimal starting phase angle when amplitude error is minimum

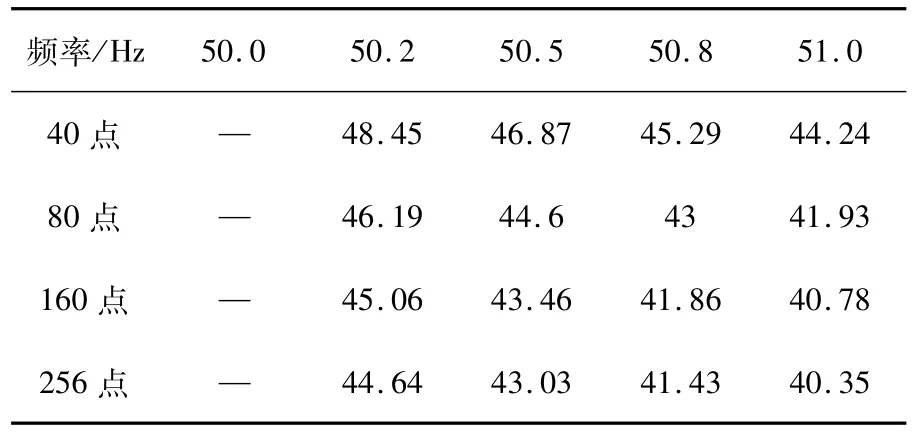
表2 频率50.0 Hz～51.1 Hz，幅值误差最小时的最优起始相位角Tab.2 Frequency 50.0 Hz～51.0 Hz，the optimal starting phase angle when amplitude error is minimum

频率在［49，50］Hz的范围内变化，相位误差最小时的最优起始相位角如表3所示。

表3 频率49.0 Hz～50.0 Hz，相位误差最小时的最优起始相位角Tab.3 Frequency 49.0 Hz～50.0 Hz，the optimal starting phase angle when phase error is minimum

频率在［50，51］Hz的范围内变化，相位误差最小时的最优起始相位角如表4所示。

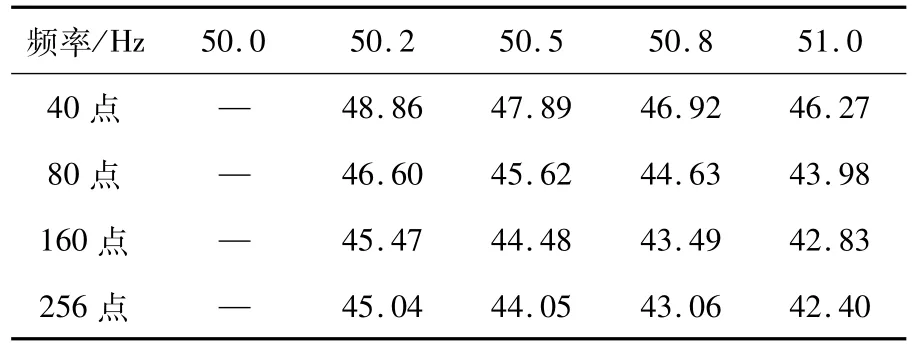
表4 频率 50.0 Hz～51.1 Hz，相位误差最小时的最优起始相位角Tab.4 Frequency 50.0 Hz～51.0 Hz，the optimal starting phase angle when phase error is minimum

表3～表4为从相位误差角度考虑，在不同采样点数和实际频率情况下的最优起始相位角。从表1～表4中的数据综合分析，在实际频率和理论频率均为50 Hz时，从任意起始相位角开始采样，均没有相位误差。幅值误差最优起始相位角和相位误差最优起始相位角变化规律相同。然而，从两个角度考虑的最优起始相位角仍不完全相等。可根据需要，选择倾向于其中一个的最优值，或在两者之间加权综合考虑。

3.2 误差曲线

本文以智能变电站最常用的每周期80点为例，仿真在各种情况下的幅值误差和相位误差。在其他点数下，变化规律完全相同，仿真得到幅值误差绝对值变化曲线如图1所示。

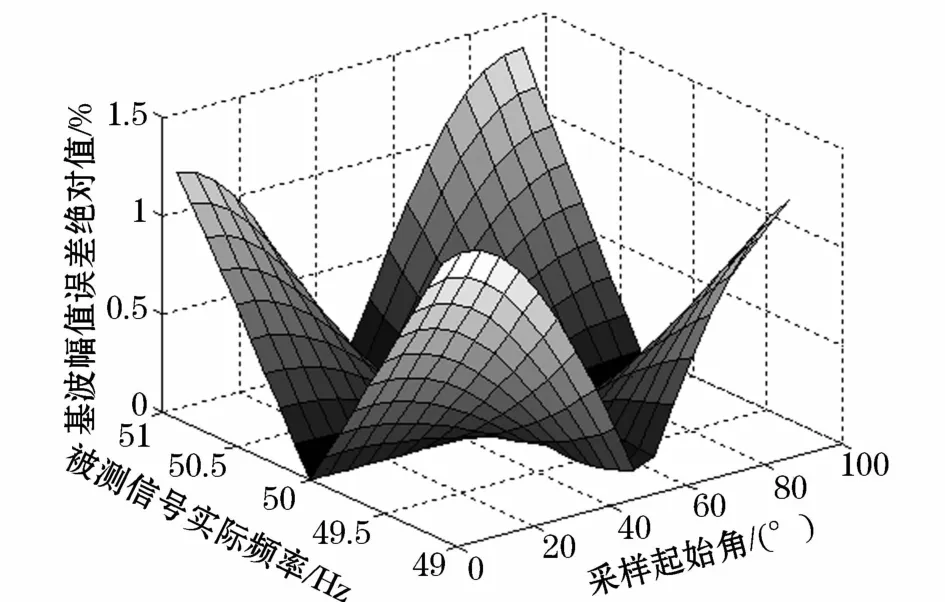
图1 幅值误差绝对值变化曲线Fig.1 Absolute value curves of amplitude errors

从图1看出，在本文规定的实际电网频率范围内，按照式（10）找到的最优起始相位角，能够使幅值误差完全为0。仿真得到相位误差绝对值变化曲线如图2所示。

从图2可以看出，在实际频率和理论频率不相等的情况下，按照式（19）找到的最优起始相位角不能完全消除相位误差。只能使相位误差相对最小，仍需要根据式（11）进行补偿。

图2 相位误差绝对值变化曲线Fig.2 Absolute value curves of phase errors

4 结束语

在精度要求不高而实时性要求高的应用场合，可大致在45°起始相位附近截取数据进行计算，再根据本文算法补偿，误差相对较小。

在精度要求高的场合，根据本文公式准确选取最优起始相位角，再进行相应补偿。理论上可以完全消除误差。

在现场工作条件下，考虑到高次谐波分量的干扰，本文算法不能完全消除误差，但仍能显著减少误差。