基于继电保护隐藏故障的系统连锁故障风险评估*

高斯泊，董博

（上海电力学院电气工程学院，上海200090）

0 引 言

近年来，电网的大规模互联已经成为全球发展的一种趋势。它增加了现代电网的规模，并提高了其经济性［1］。因此对电力系统安全和稳定运行的要求越来越高。继电保护的隐藏故障俨然成为电力系统的一种灾难性机理［2］。同时也因为互联网络的各种不确定性和系统操作行为的复杂程度而使得对于隐藏故障的风险评估愈发困难［3-4］。

目前电力系统的风险评估分为确定性评估方法和不确定评估方法两类。其中确定性评估方法主要有基于复杂网络理论的风险评估方法和基于暂态稳定分析的风险评估方法。通过提出一系列指标来进行系统关键线路的识别，如电气介数［5］、灵敏度指标［6］、支路脆弱性指标［7］等，然而这些指标的计算是以系统在故障状态下能够维持稳定为前提，并未考虑系统中一些不确定因素如恶劣天气和人员操作失误对系统安全稳定造成的影响。不确定性评估方法主要是基于概率论的风险评估方法，根据风险理论，将故障发生的概率与后果的乘积当作风险指标值作为评估的依据，采用蒙特卡洛模拟法对系统进行脆弱性评估。但程序复杂，计算量较大。考虑到熵在风险评估中对一些无序性数据处理中的便捷性与适用性，一些文献将其运用于电网安全运行的分析之中。文献［8］中采用潮流分布熵和潮流转移熵找到连锁故障传播中的脆弱元件。文献［9］采用结构效用风险熵筛选出对系统潮流转移或分布特性影响较大的脆弱支路。计算速度快，符合实际情况。但系统中的大量故障信息在风险评估中未能得到很好的体现。

在综合分析上述文献优缺点的基础上，考虑到由硬件老化、员工误操作及恶劣环境等因素引发的继电保护隐藏故障，提出一种新的继电保护隐藏故障风险评估方法。在研究隐藏故障成因的基础上建立隐藏故障概率模型，通过定义不同的风险评估指标对系统故障后的电气量进行处理，利用熵权双基点法与风险理论，计算出各条线路的风险贴近度，根据风险贴近度大小辨识出系统中的脆弱线路。最后结合算例仿真对系统进行评估分析，验证了方法的有效性与正确性。

1 继电保护隐藏故障风险评估模型

继电保护作为电力系统第一道防线，其动作特性与电网安全密切相关［10］，分析继电保护隐藏故障特性从而建立隐藏故障概率模型成为电网风险评估的重要环节。目前已经提出的隐藏故障的概率模型主要有线路距离保护隐藏故障概率模型和过电流保护隐藏故障概率模型。

1.1 线路距离保护Ⅲ段隐藏故障概率模型

故障发生后系统的潮流发生改变，容易造成线路相间距离保护Ⅲ段误动，线路距离保护Ⅲ段的隐藏故障概率模型［11］如图1所示。

图1 线路距离保护Ⅲ段的隐藏故障特性Fig.1 Hidden failure characteristics of line distance protectionⅢ

纵坐标即隐藏故障概率的大小与保护装置的测量阻抗Z有关，当保护装置的测量阻抗小于3倍距离保护Ⅲ段的设定值3ZⅢ时，隐藏故障的概率为常数PL；当Z＞3ZⅢ时，隐藏故障的概率按指数规律减小。

1.2 线路过电流保护隐藏故障概率模型

当故障切除后，电网拓扑结构发生改变，易造成线路过电流保护误动，过电流保护隐藏故障概率模型［12］如图 2所示。

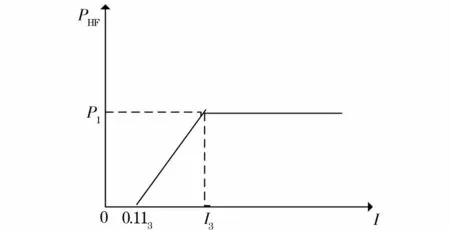
图2 线路过电流保护的隐藏故障特性Fig.2 Hidden failure characteristics of over-current protection

纵坐标PHF表示隐藏故障的概率，横坐标为线路电流值，当线路电流I大于过流保护的整定值IⅢ时，隐藏故障的概率为常数PI；而当线路电流I在IⅢ和0.1IⅢ的范围内时隐藏故障的概率按线性规律下降，在线路电流I小于0.1IⅢ时隐藏故障的概率降为0。

图1和图2均为某个单一保护的隐藏故障不正确动作情况，实际中往往有多重保护互为备用，对于保护拒动的元件，其他保护将会进行故障隔离，也有可能引起连锁跳闸，扩大故障的范围，引发连锁故障。

1.3 线路过负荷保护隐藏故障概率模型

文献［13］中认为隐藏故障发生的概率与线路潮流有关，提出了基于潮流越限的线路过负荷保护隐藏故障概率模型，如图3所示。

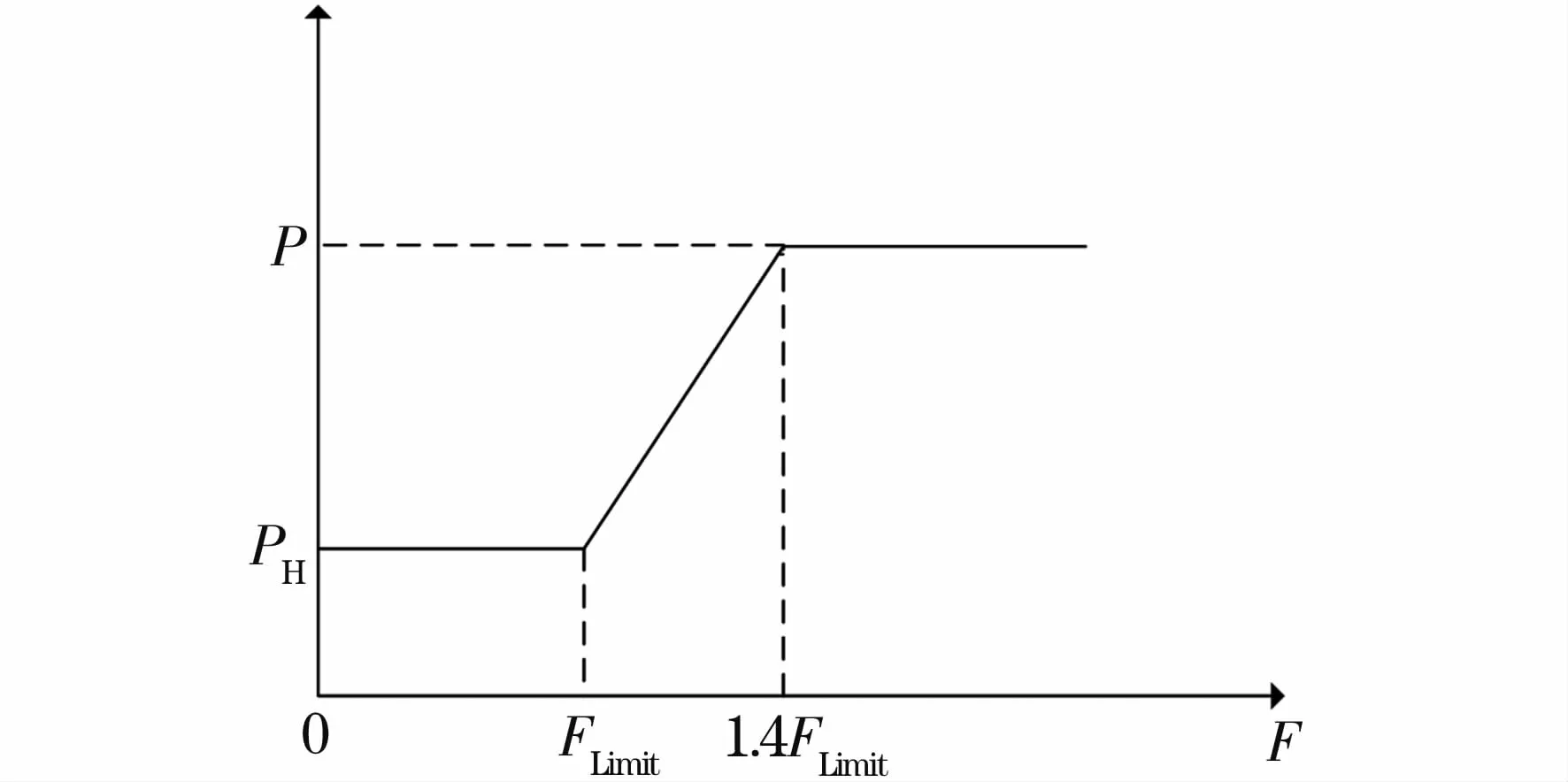
图3 线路过负荷保护的隐藏故障特性Fig.3 Hidden failure characteristics of over-load protection

其中F为线路的有功潮流，P为继电保护动作的概率，PH为隐藏故障发生的概率。

对于隐藏故障，导致保护误动的因素纷繁复杂，而过负荷保护的隐藏故障概率模型对线路保护动作进行了简化，并且在断开有限条线路后才去强制优化控制措施来消除线路过载以达到系统稳定。故本文采用图3所示的过负荷保护隐藏故障概率模型来描述电力系统线路保护装置的隐藏故障动作概率。

2 基于熵权双基点法的连锁故障风险评估

2.1 连锁故障风险评估指标

电力系统连锁故障的过程中含有大量不确定的复杂因素，具体结果体现为系统解列。而风险评估方法可以对连锁故障所造成的影响进行量化，从而比较全面的反应其发展过程及对系统造成的影响。一般将系统的风险值定义为故障发生的概率与故障发生后严重程度的乘积：

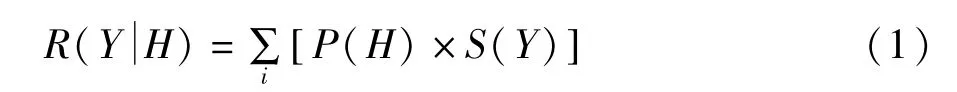
式中R（Y｜H）为系统的风险指标值；Y为系统特定的运行状态，如线路过载，电压越限等；H表示系统发生不确定性故障；P（H）为不确定性故障发生的概率，本文中采用隐藏故障发生的概率；S（Y）为系统运行在状态Y下事故的严重程度。为了能够准确的反映不同事故的相对严重程度，事故的严重度函数采用效用风险理论中的风险偏好型效用指数函数。严重度表示为：

式中W为故障损失值；S（W）为故障严重程度。

电力系统连锁故障中线路的电压、电流及频率等电气量特征越限的严重程度，可以作为风险评估的评价指标，通过严重度函数，计算出风险指标值。

（1）过负荷风险指标

过负荷风险的严重度函数如图4所示。

图4 过负荷严重度函数Fig.4 Severity function of over-load

线路 i的过负荷严重度为：SL（Y）＝0.582（eWi-1）。其中，Li为实际电流与额定电流的比值。

则过负荷风险指标的值为：

（2）失负荷风险指标

电力系统中负荷的损失与用户的类别、停电容量、停电频率、停电持续时间等因素密切相关。在此定义事故后负荷的损失率为：

式中 φFL为事故后损失的电量；φSL为系统总电量。

则支路i的失负荷严重度为：

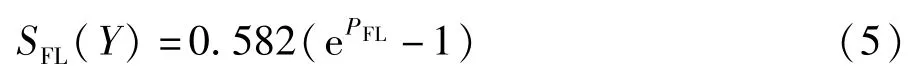
失负荷风险指标的值为：

（3）电压失稳风险指标

本文采用电压偏离正常值的严重度函数来反应系统事故的后果，电压失稳风险指标的值为：

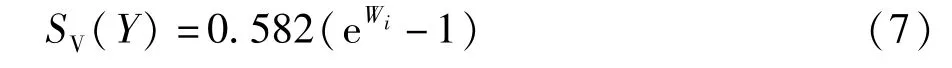
式中Wi为母线i的电压偏离值，电压失稳严重度函数如图5所示，当母线电压等于额定电压时，风险严重度为0，随着偏离值的增加，电压失稳的风险严重程度也随之增加。

图5 电压失稳严重度函数Fig.5 Severity function of voltage instability

电压失稳风险指标的值为：

（4）频率偏移风险指标

与电压失稳风险指标求取类似，采用发电机频率偏移正常值的严重度函数来反映事故的后果。频率偏移严重度函数Sf（Y）如图6所示。横坐标为发电机频率与额定频率的比值。

图6 频率偏移严重度函数Fig.6 Severity function of frequency deviation

频率偏移风险指标的值为：

2.2 熵权双基点法的原理及应用

熵权双基点法是将风险指标的熵权作为加权评价矩阵的权重系数，用以确定双基点。通过计算评价对象相对于理想点的相对贴近度求得风险程度最优排序［14］。根据风险贴近度最大原则，贴近度最大的评价对象风险程度最高。在传统的风险评估方法中，权重系数由专家经验得到，一般为固定值，往往由于其主观因素而与现实中的系统不相吻合。本文中，权重系数的值可以通过熵原理由熵权得到，它对于一些相对重要的风险指标有一定程度的倾向，同时熵权的设置可以随连锁故障的过程改变而改变。

对于一个风险评估项目，其中含有m个评价指标和n个评价对象，可以基于每个评价对象得到一个评估矩阵X，矩阵元素xij表示第i个评价指标在第j个评价对象上的值。为了便于数据的处理，消除不同维度数据之间的差异，需要对矩阵X进行标准化处理，标准化公式如下：

采用公式（10）进行标准化，从而可以得到标准化矩阵：

第i个评价指标的熵计算公式为：

第i个评价指标的熵权可以表示为：

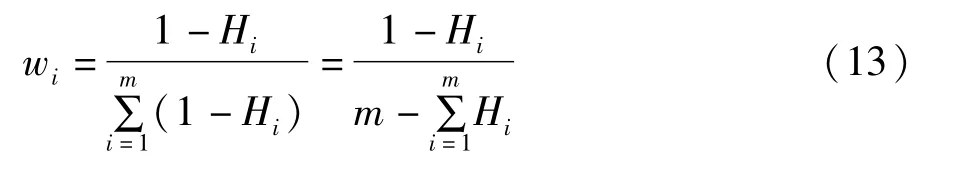
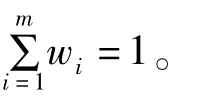
利用熵权作为评价指标的权重系数对标准化后的评价矩阵X′进行加权得到加权矩阵P。

设P*和P*分别为上述加权矩阵P的理想点和反理想点。则：

其中：

矩阵P是在标准化的矩阵加权基础上得到，因此反理想点 P*＝( 0 ，0，…，0)T，设 Pj＝（p1j，p2j，…，pmj）T，j＝1，2…n评价对象与理想点的相对贴近度计算公式为：

可以进一步简化为：

相对贴近度dj越大，则线路发生连锁故障的风险越大。对于有着多个评价指标和评价对象的复杂电力系统，可以计算出系统中所有线路的风险贴近度，从而根据贴近度最大原则，得到系统线路的风险程度最优排序。

3 算例分析

本文采用电磁暂态软件PSCAD／EMTDC搭建了新英格兰10机39节点系统作为测试系统，电压等级为220 kV，系统单线图及支路编号如图7所示。采用线路过负荷保护隐藏故障模型，暂不考虑发电机及变压器的隐藏故障，且重合闸在线路故障后不启动。

随机选取线路，发生三相短路故障，通过对全国220 kV及以上交流系统的继电保护装置动作情况进行分析，取 P（H）＝0.000 4［15］，对系统进行连锁故障的仿真，具体仿真流程为：

图7 IEEE10机39节点系统Fig.7 IEEE 10-generator 39-bus system

（1）随机选取初始故障线路；

（2）判断故障线路末端潮流是否超过1.4Flimit。若超过，则相邻支路跳闸。若未超过，则按照隐藏故障概率模型计算所得概率大小来判断相邻线路是否跳闸；

（3）线路跳闸后系统结构发生改变，检查系统是否处于稳定状态，如一段时间后仍处于不稳定状态，则采用切负荷方案使系统稳定。若线路跳闸处于快速相继跳开状态，则不采取切负荷措施；

（4）对系统进行潮流计算。检查系统中是否存在严重的故障后果，若存在负荷孤立、电源孤立、电网解列三种情况中的一种，则连锁故障过程终止，单次仿真结束；

（5）重复步骤（1）～步骤（4），计算其他线路造成连锁故障的各个风险指标值并进行相应的数据分析。

利用文中方法得到故障线路的四个风险指标值，列出部分线路的风险指标值如表1所示。

表1 线路故障的各个风险指标值Tab.1 Cascading failure risk indices of line fault

通过表1中的风险指标值构建评估矩阵，矩阵中的行为评价指标即文中四个风险指标，列为评价对象即故障线路序号，利用熵权双基点法，得出系统中所有线路的风险贴近度如图8所示。

根据风险贴近度的计算结果选取造成系统连锁故障风险最大的8条线路，其排序如表2所示。

综合表1和表2可以看出：虽然线路18的过电压失稳风险值及频率偏移风险值大于线路23，但其失负荷风险值和过负荷风险值要小于线路23。利用熵权双基点法可以很好地整合这些数据，从而准确的得到风险评估的结果：线路23发生连锁故障的风险要大于线路18。

图8 系统中的线路风险贴近度Fig.8 Risk degree of line in the system

表2 线路故障综合风险排序Tab.2 Comprehensive risk ranking of cascading failure

为了便于比较，分别用潮流熵指标［8］、事故链风险指标［16］判别所得结果与本文结果进行对比，如表3所示。从表3中可以看出，风险程度较高的线路分布趋势大体一致，验证了本文方法的有效性。但本文采取故障概率跳闸方法，并考虑到连锁故障到达一定的程度后采取强制优化措施，从而更贴近实际，判别所得的脆弱线路也更具有合理性。

表3 各方法判别所得脆弱线路比较Tab.3 Comparison of vulnerability identification of lines

对于风险排序靠前的线路，如线路9和线路11，风险贴近度较高，为易发生连锁故障的关键性线路，应重点加强监控。

4 结束语

考虑到电力系统中潜在的隐藏故障，并结合熵权双基点的算法，提出一种继电保护隐藏故障风险评估新方法，并基于此方法识别出10机39节点系统中的关键性线路，找到系统中的脆弱环节，消除了隐藏故障风险评估中的主观因素，提高了线路甄别的准确性。

为减少隐藏故障的发生，针对风险程度较高的关键性线路应采取相应的改进措施。如提高线路的负载率，对关键性线路的继电保护装置进行更新和维护，并设置合理的继电保护定值来降低继电保护隐藏故障的发生的概率。