VSC-HVDC互联系统的改进前馈控制策略

邓旗，张英敏，李兴源

（四川大学 电气信息学院，成都610065）

0 引 言

近年来，随着大容量全控性电力电子器件和智能控制技术的进步，柔性直流输电技术得到了迅速的发展。柔性直流输电技术以其不会出现换相失败、良好的动态无功支撑、可实现有功和无功的独立控制、潮流翻转时电压极性不变、可向弱交流电网供电以及无源网络供电［1-4］等优势，已被广泛应用于异步电网互联［5］、新能源的接入［6］、孤岛无源网络供电［7］当中。

在VSC-HVDC系统中，控制器是保证系统稳定运行的核心部分。目前，柔性直流输电系统中的主要控制策略为间接电流控制［8-9］和直接电流控制，其中研究最多、应用最广而且性能较稳定的控制策略是基于d-q同步旋转坐标系下的电压电流双闭环直接电流控制，在同步旋转坐标系的变换下，交流电流被分解为有功电流和无功电流分量，实现了交流量变为直流量，由于比例积分（Proportional Integral，PI）控制器积分环节的直流增益为无穷大，因此可以实现电流的稳态误差为零。文献［10］采用合成矢量建立了系统的合成矢量模型，并且提出了电流误差前馈解耦控制策略，取得了较理想的效果，但是该方法实现相对困难，不利于工程的应用。文献［11］通过对影响电流响应的因素进行了理论分析，提出了一种加快电流动态响应速度的控制策略。对于在旋转坐标系下产生的耦合电动势使得d轴和q轴不能独立控制的问题，文献［12-13］在合成矢量的基础上提出了一种没有电感参数的解耦控制器，避免了传统的双闭环控制必须精确测量电感值，彻底消除了由于电感的非线性特性引起的测量值误差，从而不受系统运行条件的变化而解耦不彻底，但是由于无电感值的解耦控制器中含有积分环节，这必然会在积分运算中出现滞后效应，响应速度要比传统的双闭环解耦控制器慢。文献［14］在矢量控制中，对PI控制器选用实系数和复系数两种情况进行了本质性的分析，从矢量控制的解耦性、电流环的抗扰动能力、控制器参数的鲁棒性三方面揭示了实系数与复系数控制器的差别，仿真和物理实验均表明相对于直接前馈补偿方式的解耦，基于复系数的间接前馈补偿解耦方式由于前馈控制器中含有积分环节，动态性能有明显的不足，而且在抵抗外部的扰动能力方面也相对较弱。从而表明文献［12-13］在设计无电感的解耦控制器时，没有全面考虑到该控制器和传统双闭环解耦控制器的优劣，认为所设计的基于复系数PI控制器能省略掉交叉耦合项的说法是片面的。

本文在文献［14］VSC-HVDC系统中采用直接电流控制的直接前馈解耦控制策略基础上，针对其直接前馈控制跟踪目标值契合度低、响应速度较慢的缺点，对整流侧定有功功率控制和逆变侧定直流电压控制，提出一种改进的前馈控制策略，最后基于PSCAD／EMTDC的仿真验证表明，所提出的改进前馈控制策略在跟踪目标值时有较高的契合度，系统的响应速度得到提高，并且抗扰能力加强，整个设计过程简单，便于工程实践。

1 VSC-HVDC系统的拓扑结构

1.1 电流内环控制器

在本文的研究中只考虑交流系统的基波分量。三相两电平换流器的一端如图1所示。

图1 三相电压型PWM整流器ig.1 Three-phase voltage-sourced PWM rectifier

图中参数的物理意义在文献［12，15-16］中已经有详细介绍。在同步旋转d-q坐标系下可建立式（1）所示VSC-HVDC系统的数学模型。

式中表明 d、q轴电流受到交叉耦合项 ωLisd、ωLisq的影响不能独立的进行控制。

比例积分控制器由于具有能实现对直流量的无静差追踪［17］，良好的全局稳定性，鲁棒性好等优势，在工程实践中得到了广泛的应用，在经过d-q旋转坐标系的变化后，isd、isq变为直流量。由内模理论可知，输出能稳态无偏差的跟踪输入的前提是闭环内含有输入的模型。当输入为阶跃时其在复域中的模型包含有1／s，而传统的PI控制器由于含有积分环节，因此PI控制器能实现对输入阶跃的无静差跟踪［18］。在经过旋转坐标变换后，被控对象的极点将由实数变为复数，在变换的过程中会产生一个附加的旋转电动势，正是这两个电动势的存在使得d轴和q轴的电流控制存在耦合，因此通常在VSC-HVDC系统中采用双闭环来实现d轴和q轴的彻底解耦，其中内环实现电流无静差的追踪，外环提供内环所需要的电流整定值，基于d-q同步旋转坐标系的内环电流前馈解耦控制框图如图2所示，图2表明在经过同步旋转坐标系变换后引入的交叉耦合项可以通过电流的前馈控制来抵消，从而实现了d（q）轴电流isd（isq）只受d（q）轴的参考电流的控制，与 q（d）轴的参考电流无关。

图2 同步旋转d-q坐标系下的电流解耦控制框图Fig.2 Decoupling control block diagram in synchronous rotating d-q reference frame

1.2 电流外环控制器

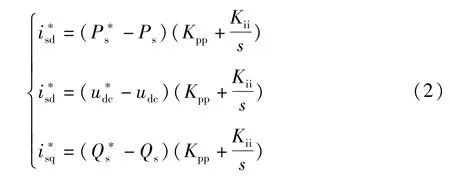
式中Kpp、Kii分别为电流外环中PI环节的比例和积分系数。结合内环的前馈解耦控制，可以实现在整流侧对有功功率、无功功率以及在逆变侧对直流电压、无功功率的独立且静态无差调节，能够保证系统具有良好的动态性能。

2 改进电流环前馈控制策略

2.1 有功功率的前馈控制

由于电流内环d轴和q轴的对称性，文中以d轴为例来说明前馈控制策略。由图2可得：

式中Kp、Ki分别为电流内环PI环节的参数。

考虑到换流器具有一定的惯性，用时间常数为Tδ的一阶环节来等效换流器的延时［19］，其中 Tδ为PWM的采样周期，即：

联立式（1）、式（3）、式（4）并在稳定工作点附近进行线性化（泰勒展开式忽略高次项后）可得：

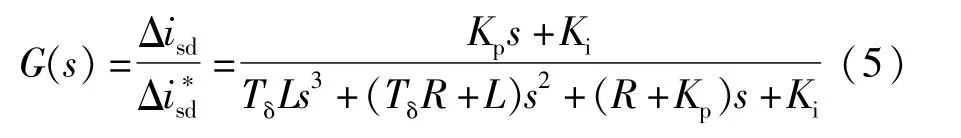
为了避免电流内环和电压外环之间的相互影响，一般情况下，使电压外环的带宽远小于电流内环的带宽，从而在分析电压外环时可以近似把电流内环看作一个比例环节［20］，由于PWM的开关频率很高，对式（5）进行降阶处理，忽略式（5）中的二次以及三次项后：

在外环控制中，当以usd为d轴的参考方向时，可得：

对式（7）线性化可得：

式中usd0表示其在稳定工作点的值。

由以上的分析可得已解耦的d轴电流环框图如图3所示。

图3 有功功率功率控制框图Fig.3 Block diagram of active power control

为了能对有功功率信号更好的预测，本文在电流环的基础上增加前馈控制，将预测值添加到电流内环的输入中，增加的前馈控制可以有效地解决反馈信号的滞后性，降低控制量的误差值，提高系统的响应速度。改进后的电流环前馈控制框图如图4所示。

图4 改进的有功功率前馈控制框图Fig.4 Block diagram of the improved active power feedforward control

加入前馈控制的目的是使系统的输出量在任何时刻都能与输入量相等，系统的稳态和暂态误差均为0，但是由于系统受阻尼作用的影响以及等效的准确性和延时估计的不确定性，系统不可能具有理想的跟踪性。加入前馈控制后有功功率闭环传递函数为：

为了达到输出能很好的跟踪输入，使H（s）＝1，由此可知 KF（s）G（s）＝1，即：

按式（10）计算前馈控制函数F（s），在理论上可使系统的闭环传递函数H（s）＝1，以达到更好跟踪整定值的目的。

2.2 直流电压的前馈控制

对于VSC-HVDC系统中的定直流电压控制，控制策略的目的是使换流器两侧传输的功率保持平衡，即使Ps＝Pdc。在图1中，忽略电阻损耗和开关器件的损耗，有：

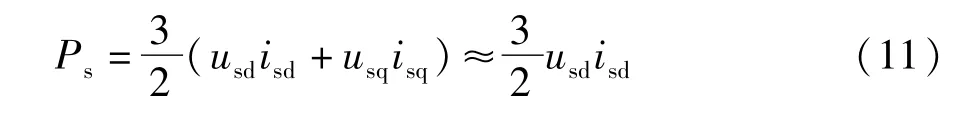
而在换流器的直流侧，有：

由于电流内环快速的动态调节性能，认为isd＝由式（13）可得到，直流电压与网侧电压usd以及直流线路电流il有关。在原有的定直流电压控制中增加一个前馈控制［21］：

带入式（13）中可得：

式（15）表明，在稳态时，直流电压和网侧电压、直流线路电流都无关，当传输的功率或者电网电压波动时，前馈信号式（14）都能很好的跟踪整定值的变化，快速调整线路电流，从而维持换流站两侧的功率平衡，保持直流电压的稳定。通过以上的分析可以得到改进的定直流电压前馈控制策略的框图如图5所示。

图5 改进的直流电压前馈控制框图Fig.5 Block diagram of the improved DC voltage feedforward control

3 仿真分析

为验证所提控制策略的有效性，在PSCAD／EMTDC中搭建了一个两端的VSC-HVDC系统进行仿真分析，系统的结构图如图6所示。

图6 两端VSC-HVDC系统结构Fig.6 Structure of two-terminal VSC-HVDC system

图6中换流站1为整流侧，换流站2为逆变侧，在双闭环控制中的定有功功率、定直流电压控制采用本文所提的改进前馈控制策略，VSC-HVDC系统的部分参数如表1所示。

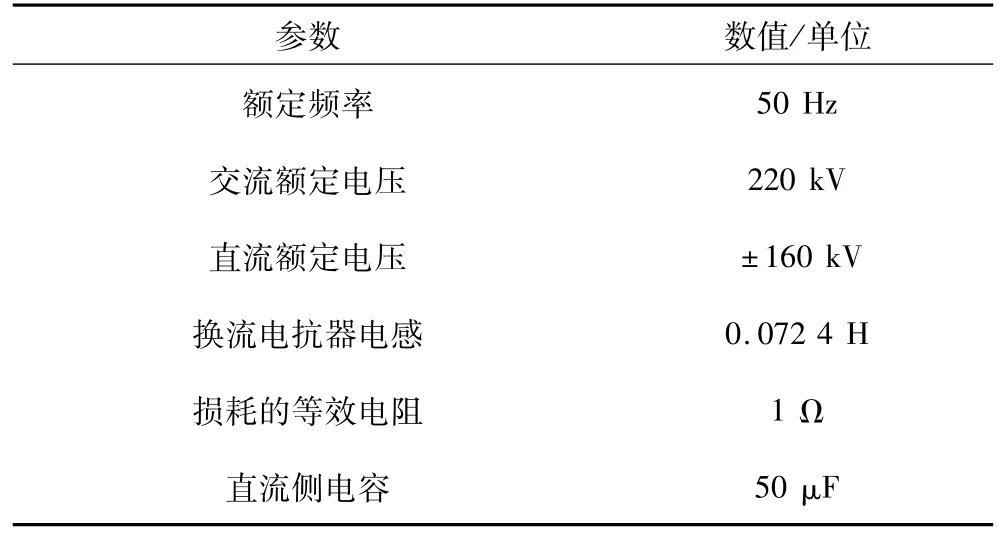
表1 两端VSC-HVDC系统参数Tab.1 Parameters of two-terminal VSC-HVDC system

3.1 整流侧有功功率的阶跃响应

初始状态下定有功功率的整定值为200 MW，为了验证所提控制策略跟随整定值的契合度，在仿真到1 s时，使有功的整定值减小100 MW，图7为整定值在发生变化后有功功率的响应曲线。

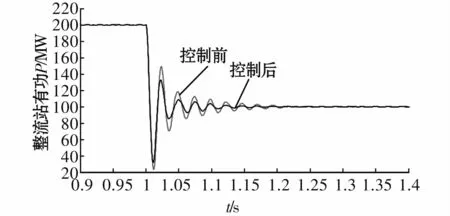
图7 有功功率的阶跃响应Fig.7 Response to step change of active power

改变初始状态下的有功整定值为100 MW，在1 s时使有功的整定值减小50 MW，以验证系统工作于不同状态下的阶跃响应曲线，如图8所示。

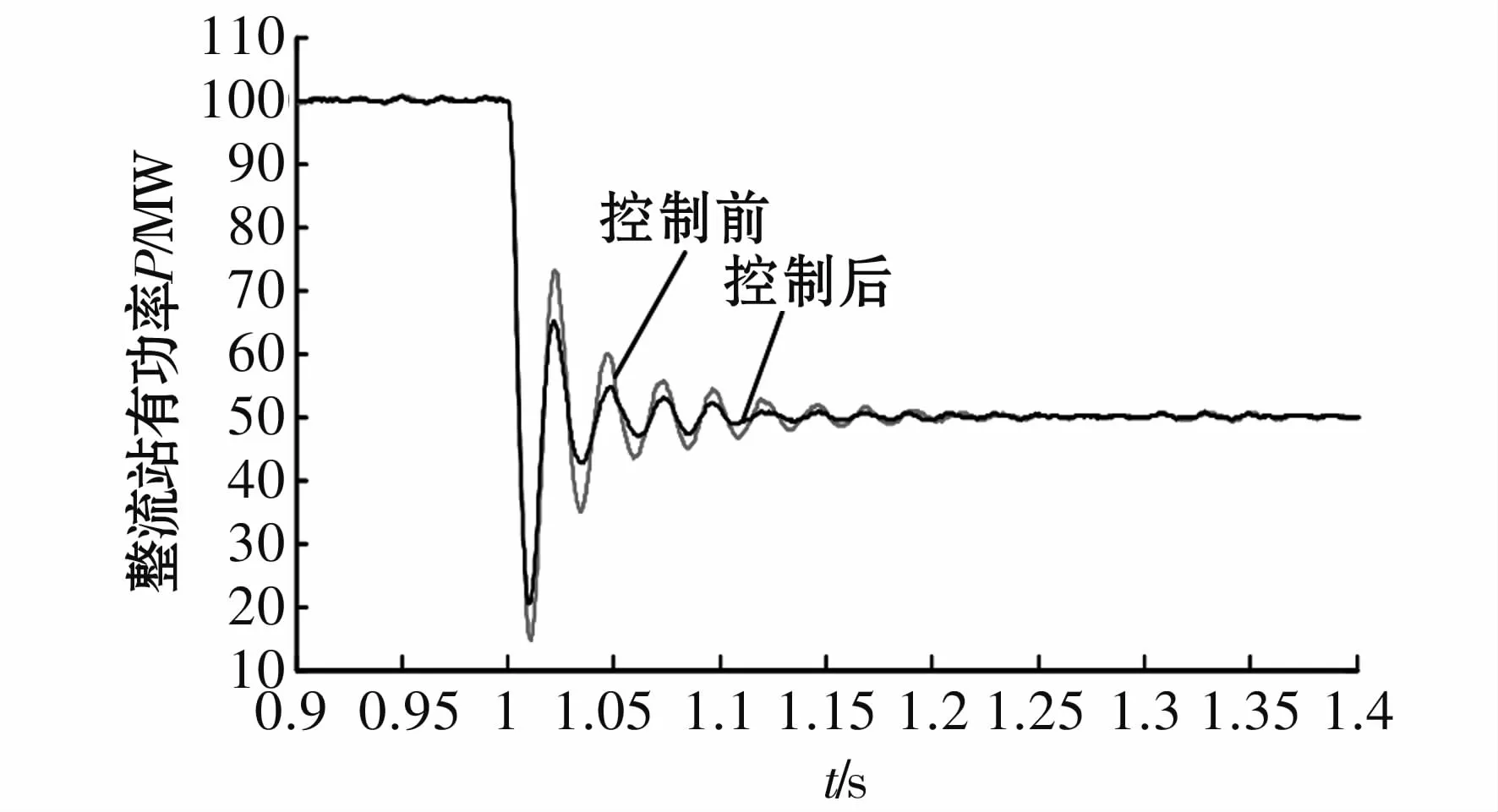
图8 有功功率的阶跃响应Fig.8 Response to step change of active power

由图7、图8可以得到，在系统工作于不同的状态，当有功功率发生阶跃变化时，运用本文所提的改进前馈控制策略相对于传统的双闭环控制对整定值的跟踪有更好的效果，契合度更高，达到稳定状态所需要的时间更短，超调量减少。

为了验证本文中改进前馈控制策略的鲁棒性，在上述两种初始状态下，使系统发生相应的潮流翻转，即在仿真时间1 s时，分别使有功的整定值变为-100 MW、-200 MW，持续时间为 0.3 s，其相应的阶跃响应曲线如图9所示。

由图9可以得到，在系统发生潮流翻转时，利用本文所提的改进前馈控制策略获得的效果要优于传统的双闭环控制，特别是在系统的恢复阶段，如在图9（b）中，双闭环控制策略发生了振荡，导致系统不稳定，而采用本文改进的前馈控制策略在潮流恢复阶段经过一定时间的振荡后，最终能使系统重新恢复到稳定状态，可见改进的前馈控制策略增加了系统的阻尼，能有效抑制故障引起的各种振荡，使系统快速稳定收敛，进一步验证了该控制策略的有效性。

3.2 逆变侧直流电压的阶跃响应

为了验证本文中定直流电压控制策略对负载扰动的抗干扰能力，针对逆变侧的定直流电压控制，在仿真进行到1 s时，分别增加和减小相同的负载量，持续时间为0.3 s，图10为直流电压的响应曲线。

图10 直流电压的响应曲线Fig.10 Response curve of DC voltage

仿真实验表明，采用改进的前馈控制策略后，系统稳态时对负载变化的扰动具有比较强的抗干扰能力，能使系统的直流电压很快的维持在一个稳定的水平。

4 结束语

本文在VSC-HVDC系统中，针对传统双闭环控制策略跟踪整定值契合度较低的问题，提出了一种基于电流环的改进前馈控制策略，在整流侧定有功功率控制中补偿一个事先预知的量，以提高整定值跟踪的响应速度，减小了系统的超调量和稳态误差；在逆变侧定直流电压控制中把网侧电压和直流电流的信息引入到内环中，用以增加系统的抗扰能力。仿真实验表明该前馈控制策略能有效增强整个系统的稳定性，为跟踪整定值提供了一种新思路，具有一定的理论价值。