基于动态非等比例双强度折减法的边坡稳定性研究

， ，，，

(1.国网山东省电力公司经济技术研究院，济南 250000；2.中国地质大学(武汉) 工程学院，武汉 430074)

基于动态非等比例双强度折减法的边坡稳定性研究

寇天1,2，胡斌2，和大钊2，毛元静2，姚文敏2

(1.国网山东省电力公司经济技术研究院，济南 250000；2.中国地质大学(武汉) 工程学院，武汉 430074)

2017,34(12):84-88

为了探究动态非等比例双强度折减法在边坡稳定性应用的可行性，基于ABAQUS软件，根据三维边坡渐进破坏的过程和强度参数在边坡中发挥作用程度的不同，通过动态非等比例的双强度折减法理论，将Mohr-Coulomb强度准则中的黏聚力c和内摩擦角φ转换为Drucker-Prager强度准则中的屈服强度σ与内摩擦角β；并利用最短路径理论确定边坡的综合稳定性系数，评价边坡的稳定性。结果表明：基于D-P强度准则的动态非等比例的双强度折减法能够更合理地反映三维边坡的渐进破坏过程及其强度参数的发挥程度；所得到的边坡稳定性系数与以M-C准则计算得到的结果非常接近，且得到的边坡稳定性系数、边坡的位移均小于传统强度折减法的模拟结果，具有更高的安全储备。该方法收敛快速，在三维边坡的稳定性计算中有一定的应用价值。

双强度折减；非等比例；D-P强度准则；ABAQUS；稳定性分析

1 研究背景

随着人类工程活动的进行，边坡的稳定性问题日益突出，边坡的三维极限平衡稳定性研究一直是热点问题，并且也取得了很多的研究成果。Duncan[1]研究认为传统的Mohr-Coulomb(M-C)屈服准则虽然比较准确，但是在三维应力空间中的屈服面存在尖顶和棱角的不连续点，从而导致数值计算不收敛。而Drucker-Prager(D-P)准则在偏平面上是个圆，不存在尖顶的数值计算问题，更适合数值模拟计算[2]。

有限元强度折减法在边坡稳定性分析中的应用非常广泛。它可以用于研究边坡失稳渐变过程和稳定性系数，克服了极限平衡法和有限元数值分析法两者的不足，具有概念明确、计算方便、结果直观的优点。随着陈国庆等[2]、Isakov等[3]、薛海斌等[4]、唐芬等[5]对其的进一步研究，不仅引入了有限元双强度折减法[6]，还在此基础上研究了黏聚力与内摩擦角的折减系数之间的比例关系及它们的衰减速度和程度，提出了双折减系数的非等比例相关关联的关系[4]，并针对双安全系数的不足，提出了最小强度折减路径理论，从而避免了双强度折减系数比例选择的随机性，得到了边坡的综合稳定性系数[3]。此外，陈国庆等[6]提出的动态强度折减法可用于分析边坡的渐进性破坏过程，这为工程边坡的稳定性研究提供了新的思路，具有一定的工程实用价值和适用性。

本文通过运用M-C强度准则和D-P强度准则中关键参数的转换关系，提出了基于D-P屈服准则的动态非等比例的双强度折减法；并运用ABAQUS软件对三维矿山边坡进行非等比例的动态双强度折减分析，研究边坡的渐进破坏过程、稳定性情况及运用ABAQUS软件的合理性，考察该方法在三维边坡稳定性数值分析中的实际效果。

2 计算原理

2.1 有限元强度折减法原理

传统的双强度折减法是将土体的抗剪强度指标c(黏聚力)和φ(内摩擦角)，用同一个强度折减系数FS进行折减，然后用折减后的抗剪强度指标cF和φF取代原来的抗剪强度指标c和φ，即：

cF=c/FS；

(1)

φF=arctan(tanφ/FS) 。

(2)

式中:c是土体的黏聚力；φ是土体的内摩擦角。

在有限元分析中，直到边坡达到临界破坏状态时的强度折减系数即为该边坡的稳定性系数FS。

2.2 动态非等比例双强度折减法

由于边坡失稳过程中黏聚力和内摩擦角发挥程度并不一定相同，很多专家学者对它们之间存在的比例关系做了大量的研究。例如，薛海斌等[4]基于岩土材料的软化规律所得到的非等比例相关联的双强度折减法，在强度参数服从线性分布假定的基础上，推导出了2个强度参数的折减系数之间的存在的非等比例关系为：

(3)

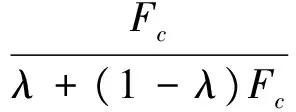
(4)

式中：φp，cp分别为峰值强度下的内摩擦角、黏聚力；φr，cr分别为残余强度下的黏摩擦角、黏聚力;Fc为黏聚力强度折减系数；Fθ为内摩擦角强度折减系数；λ为强度比例系数。

2.3 综合稳定性系数的确定方法

采用双强度折减方法时需要将双折减系数转换为单一的综合稳定性系数，用来评价实际工程中边坡稳定性安全储备，因此可以使用隐含表达式来将双强度折减系数转化为边坡的综合稳定性系数。该隐含表达式可用Isakov等[3]认为的强度折减的最短路径R来定义，其表达式为：

(5)

(6)

式中：FS,c，FS,θ分别为c和φ的稳定性系数；FS为边坡的综合稳定性系数。

2.4 屈服准则及相应理论的转换

稳定性系数的大小与采用的屈服准则密切相关，不同的屈服准则会得出不同的稳定性系数。本研究中采用理想的弹塑性模型，建立的D-P强度准则与M-C强度准则的转换关系如下所示：

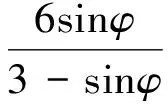
(7)

(8)

以D-P准则中的内摩擦角β和屈服强度σ取代M-C准则中的黏聚力c和内摩擦角φ，并采用非等比例的双强度折减法进行参数转换，通过ABAQUS软件建立三维数值仿真模型计算得到相应的稳定性系数。其中非等比例的双强度参数相关关系根据2个强度准则存在的关系进行推导：

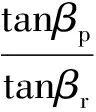
(9)

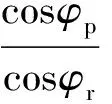
(10)

式中：βp，βr分别为峰值强度下、残余强度下的D-P准则内摩擦角；Fσ，Fβ分别为屈服强度和内摩擦角的转换系数。

式(9)、式(10)可进一步简化为：

Fσ=aFc；

(11)

Fβ=bFθ。

(12)

其中：

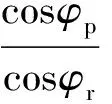
(13)

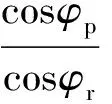
(14)

式中:当φr→φp时，a→1，且有b→1。

此时有

现在，麦田里还一片浅绿。范坚强的别墅，嵌在麦田之上。一杭走下出租车，对司机说：“不用找了，十分钟内，将有一位女士出来，你送她到天回镇。”

a≈b。

(15)

将式(13)、式(14)代入式(4)中可得

(16)

将式(15)代入式(11)、式(12)中可得

Fσ=Fc，Fβ=Fθ。

(17)

将式(17)代入式(4)可得

(18)

式中:当λ=1时，Fσ=Fβ，为传统的有限元双强度折减法的一般折减方式。

当φr→φp时，将式(17)代入式(6)可得

(19)

式中FS,σ，FS,β分别为σ和β的稳定性系数。

2.5 边坡失稳判据选择

目前的边坡数值分析中，有限元强度折减法中边坡失稳判据主要包括有限元数值迭代不收敛判据、特征部位位移突变判据、广义塑性应变或者等效塑性应变贯通判据3类[7-11]。而有限元迭代不收敛只能发生在边坡岩土体塑性区贯通或者特征部位位移突变之后，它与数值计算模型及计算准则的关联较大。因此，为了较为合理地判断边坡失稳，本文主要采用塑性区贯通和监测点位移发生突变作为边坡失稳的综合判据。

3 工程实例分析

3.1 模型概况

以四川省某石灰石矿山为研究对象，通过使用基于D-P强度准则动态非等比例的双强度折减法研究边坡的稳定性，利用最小路径理论将该准则中的内摩擦角β和屈服强度σ的折减系数转化为综合稳定性系数，最终确定边坡的稳定性情况。

峨胜矿山南侧因开挖形成了倾角为45°的边坡以及倾角为36°的台阶坡面，坡顶发现有梁山组的软弱夹层出露，在矿山开挖、爆破的生产作业以及降雨等条件下，可能发生顺层岩质滑坡，严重威胁矿山的正常生产安全。现利用D-P强度屈服准则的动态非等比例双强度折减法对矿山边坡进行稳定性评价及预测工作。利用现场勘查及钻探资料，通过ABAQUS软件，建立矿山三维边坡模型，如图1所示，自上而下的岩土材料分别为灰岩、软弱夹层、砂岩。此外在模型上设置了4个监测点A，B，C，D来监测测点的位移，其中点A、点B、点C自上而下布置在边坡坡面上，点D在软弱夹层上。

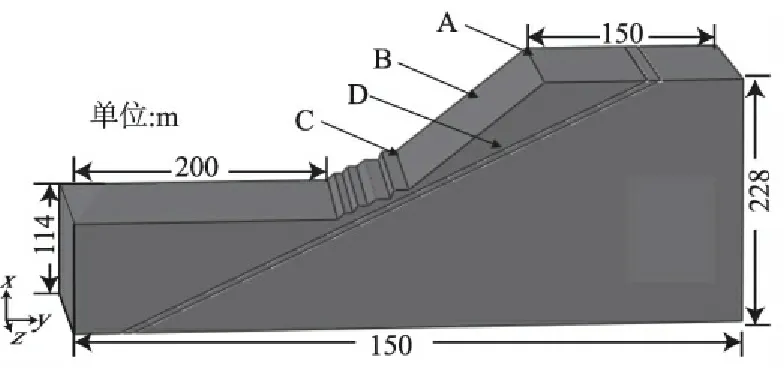
图1边坡模型

Fig.1Modeloftheslope

根据室内试验和岩体质量评价得到了矿山边坡的物理力学参数，如表1所示。

通过以上岩土体材料参数可以得到灰岩、软弱夹层、砂岩的强度比例系数分别为λ1=0.434，λ2=0.249，λ3=0.238。

3.2 基于D-P准则下稳定性结果分析

采用双强度折减法计算边坡的稳定性时，各岩体的Fσ和Fβ按照所得到的双强度折减系数的非等比例关系的3个比例系数λ1，λ2，λ3进行折减计算，详见表2。

表1 边坡的力学参数

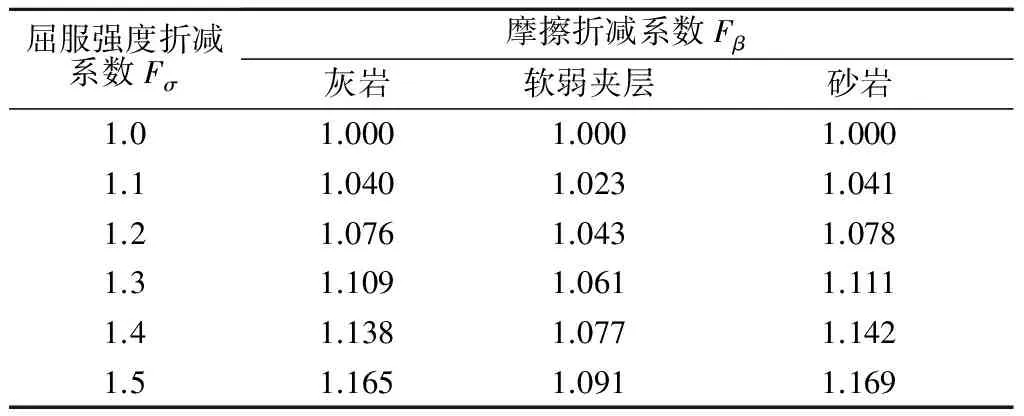
表2 3类岩石的折减系数

边坡的滑动带动态演变过程如图2所示。

(a)Fσ=1.0, Fβ=1.000

(b) Fσ=1.1, Fβ=1.023

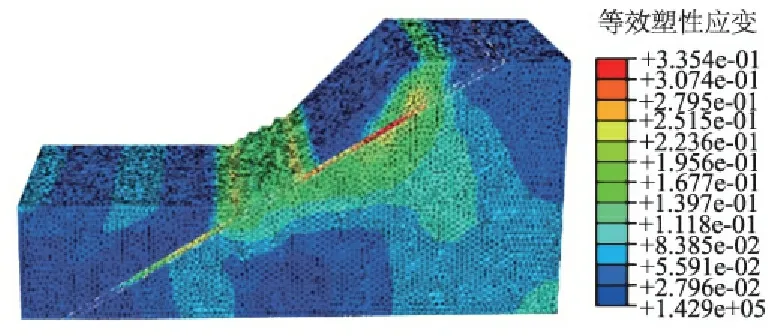
(c) Fσ=1.2, Fβ=1.043

(d)Fσ=1.3,Fβ=1.061

图2不同折减系数下的塑性区

Fig.2Plasticzonewithvaryingreductionfactor

由图2可知，随着强度参数的不断衰减，边坡中塑性区从坡角逐渐向坡顶延伸，且塑性区的范围不断扩展，当Fσ=1.3,Fβ=1.061时，边坡中的塑性区贯通至坡顶，边坡处于临界破坏状态，从双强度折减系数大小上来看，屈服强度σ对边坡稳定性的作用较大。此外，由图2可见，该边坡是沿着软弱夹层发生类折线形的滑动破坏。

综合折减系数与4个监测点的位移的关系曲线如图3所示。由图3可知，当4个监测点位移发生陡增时，可以判断该边坡将发生滑动破坏或处于临界稳定状态；所以该时刻的折减系数即为综合稳定性系数FS=1.202。此时，监测点A，B，C，D的位移分别为19.85，16.15，22.98， 20.63 cm。

图3基于D-P准则的位移与综合稳定性系数的关系曲线

Fig.3Curvesofdisplacementvs.comprehensivestabilitycoefficientbasedonD-Pcriterion

3.3 对比M-C准则下稳定性结果分析

为了验证动态强度折减法所得到的综合稳定性系数的合理性，本文亦对基于M-C强度准则的非等比的双强度折减法进行了稳定性计算，得到了相应的边坡渐进破坏的过程及稳定性系数。所得到的稳定性系数如图4、表3所示。从图4中可知，当边坡监测点的位移发生陡增时，说明边坡发生滑动破坏，此时的综合稳定性系数即为边坡的稳定性系数，其大小为FS=1.216, 对应的Fc=1.3，Fβ=1.11 。而由D-P强度准则所得到的稳定系数FS=1.202，其结果相对保守且与基于M-C准则计算结果的相对误差仅为1.15%。所以D-P强度准所得到的综合稳定性系数是合理的。

对比图3与图4可知，基于M-C强度准则的临界失稳破坏的监测点A，B，C，D的位移分别为29.20，24.86，36.98，31.64 cm。与D-P强度准则结果相比较，边坡在各监测点的位移相差很大(相对于基于M-C准则计算结果分别相差32.1%，35.0%，37.8%，36.1%)，说明该模型基于M-C强度准则的边坡临界失稳时的位移明显大于基于D-P强度准则的计算结果，即基于D-P准则计算边坡具有更高的安全储备。

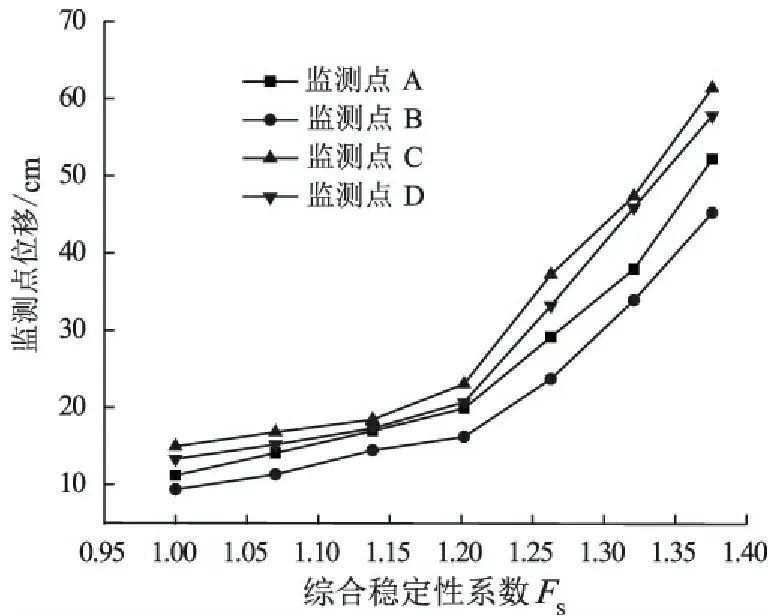
图4 基于M-C准则的位移与综合稳定性系数的关系曲线

从图5可知，M-C准则中位移扩展范围较大，而D-P准则中的最大位移多数集中在软弱夹层上方，即潜在破坏方式为以软弱夹层为滑动面的顺层折线状滑移，更符合实际。

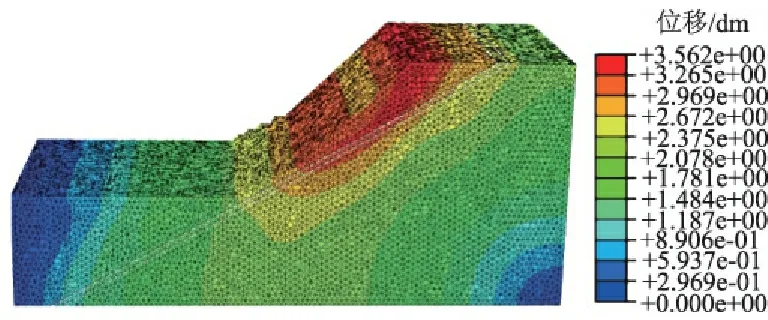
(a)D-P准则下FS=1.202

(b)M-C准则下FS=1.216

图52种准则下的位移云图

Fig.5Displacementcontoursbasedontwocriteria

综上可知，2种强度准则下边坡的变形均在可控范围内，但是D-P强度准则的模拟结果位移变形比M-C准则中位移要更小且变形位移更接近实际情况，具有更高的安全储备。这是因为D-P强度准则在三维边坡模拟过程中不仅减小了模型中尖点因素对边坡变形的影响，并且在非等比例阶段对破损区的折减更为合理。因此，基于D-P强度准则的非等比例的动态强度折减法在三维边坡中的计算结果更合理，且具有较高的安全储备。

4 结 论

(1)将基于M-C强度准则中两个强度参数折减系数在软化阶段的非等比例相关关系,引入到了D-P强度准则的动态双折减中，并在ABAQUS软件中实现了相应的模拟，得到了相对合理的稳定性系数。

(2)通过对比不同强度准则下的非等比例的动态双强度折减所得到的稳定性系数和位移情况，可知不同准则下，所得到的稳定性系数相差不大(约为1.15%)，说明基于岩土材料的软化规律所得到的非等比例相关联的双强度折减法是合理可靠的；而所获得的位移变形相差很大(最大相差37.8%)，说明基于 D-P强度准则的非等比例的动态双强度折减法获得的稳定系数具有更高的安全储备。表明基于D-P强度准则的非等比例的动态双强度折减法更加可靠和合理。

(3)从实际的运算速度来讲，D-P强度准则在三维边坡模拟中更具有优势，不仅能实现三维边坡快速收敛，更能够得到合理的稳定性结论。在今后三维边坡的稳定性计算中具有一定的应用价值。

[1] DUNCAN J M. State of the Art: Limit Equilibrium and Finite Element Analysis of Slopes[J]. Journal of Geotechnical Engineering，1996, 122(7):577-596.

[2] 陈国庆，黄润秋，周 辉,等.边坡渐进破坏的动态强度折减法研究[J].岩土力学,2013,34(4):1140-1146.

[3] ISAKOV A, MORYACHKOV Y. Estimation of Slope Stability with Using Two-parameter Criterion of Stability[J]. International Journal of Geomechanics,2013，14(3):613-624.

[4] 薛海斌，党发宁，尹小涛,等.边坡强度参数非等比例相关联折减法研究[J].岩土力学与工程学报,2015，34(增2)：4005-4012.

[5] 唐 芬，郑颖人.边坡稳定安全储备的双折减系数推导[J].重庆交通大学学报(自然科学版),2007,26(4)：95-100.

[6] 陈国庆，黄润秋，石豫川,等.基于动态和整体强度折减法的边坡稳定性分析[J].岩石力学与工程学报，2014,33(2): 243-256.

[7] 年廷凯,张克利,刘红帅,等.基于强度折减法的三维边坡稳定性与破坏机制[J].吉林大学学报(地球科学版), 2013,43 (1):178-185.

[8] 赵尚毅，郑颖人，张玉芳.极限分析有限元法讲座——Ⅱ有限元强度折减法中边坡失稳的判据探讨[J].岩土力学，2005,26(2):332-336.

[9] 宋雅坤，郑颖人，赵尚毅，等.有限元强度折减法在三维边坡中的应用研究[J].地下空间与工程学报，2006，2(5):822-827.

[10] 裴利剑,屈本宁,钱闪光.有限元强度折减法边坡失稳判据的统一性[J].岩土力学, 2010,31(10):3337-3341.

[11] 曹 婷，张光碧，邱珍锋.剪胀角对分层边坡稳定性的影响[J].南水北调与水利科技，2013,11(3): 67-70.

Slope Stability Analysis Based on Non-proportional and Dynamic Double Strength Reduction Method

KOU Tian1,2, HU Bin2, HE Da-zhao2，MAO Yuan-jing2，YAO Wen-min2

(1.Economic & Technology Research Institute, State Grid Shangdong Electric Power Company, Jinan 250000, China；2.Faculty of Engineering, China University of Geosciences, Wuhan 430074,China)

The aim of this research is to investigate the feasibility of non-proportional dynamic double strength reduction method in slope stability analysis. According to the 3-D progressive failure process and strength parameters of slope in ABAQUS software, the cohesioncand internal friction angleφin Mohr-Coulomb strength criterion are converted into yield strengthσand internal friction angleβin Drucker-Prager strength criterion, and then the comprehensive stability coefficient of slope is determined through the shortest path to evaluate the slope stability. Results suggest that the non-proportional dynamic double strength reduction method based on Drucker-Prager criterion could reflect the progressive failure process and the roles of strength parameters; the slope stability coefficient obtained by Drucker-Prager criterion is highly close to that calculated by the M-C strength criterion, and the slope stability coefficient and displacement are both smaller than those of traditional strength reduction results with higher safety reserve.

double strength reduction; non-proportional; D-P strength criterion; ABAQUS; stability analysis

10.11988/ckyyb.20160797

2016-08-09;

2016-09-02

国家自然科学基金面上项目(41172281);国家科技部973项目(2011CB710604)

寇 天(1990-)，男，山东淄博人,硕士研究生，主要从事边坡稳定性分析、数值模拟研究，(电话)13853157897(电子信箱)1461179131@qq.com。

胡 斌(1974-)，男，山东曲阜人，教授，博士生导师，博士，主要从事边坡稳定性分析、岩土工程数值模拟研究，(电话)13297940657(电子信箱)40275083@qq.com。

TU452

A

1001-5485(2017)12-0084-05

(编辑：占学军)