挠性支承可倾瓦轴承完整动力学建模及分析

杨期江，李伟光，赵学智，滕宪斌

（1.广州航海学院 轮机工程学院，广州 510725；2.华南理工大学 机械与汽车工程学院，广州 510640）

挠性支承可倾瓦轴承完整动力学建模及分析

杨期江1，李伟光2，赵学智2，滕宪斌1

（1.广州航海学院 轮机工程学院，广州 510725；2.华南理工大学 机械与汽车工程学院，广州 510640）

考虑动压润滑油膜温粘效应，首先建立轴颈-瓦块相对几何关系，导出支点反作用力与力矩的0阶与1阶泰勒展开方程，推导瓦块油膜力、力矩的平衡方程及其刚度阻尼系数，联合轴颈-瓦块运动的微分方程，建立挠性支承可倾瓦轴承完整动力学模型；通过与相关文献的试验数据进行对比分析，验证所提出的挠性支承可倾瓦轴承完整动力学模型的准确性。

振动与波；挠性支承；可倾瓦轴承；完整动力学模型

挠性支承可倾瓦轴承（Flexure Pivot Tilt Pad Bearing，简称FTPB）通过挠性支承（如图1所示）实现轴瓦支承点的弯扭耦合，实现相同的低交叉耦合，具有高稳定性，消除了传统机械支点存在的磨损和高接触应力现象。

图1 传统机械支点与挠性支点

挠性支承可倾瓦轴承采用电火花技术加工轴瓦，瓦块与壳体之间通过挠性梁连接，使其成为一个整体。这种设计消除了瓦块与壳体的装配误差、支点疲劳、瓦块卸载的颤振问题等传统可倾瓦轴承的缺陷[1]。目前国外在该领域发展的方向为：

(1)与挤压油膜阻尼器串联组成全新的阻尼减振滑动轴承[2–3]；

(2)将该类型结构的轴承应用于无油透平机械如微型燃气轮机，改用空气作为润滑剂，大大拓宽了其工作转速与温度[4]；

(3)引入流体静压，发展成为动静压混合润滑轴承[5–6]。国内Kai Feng等提出了一种挠性支撑可倾瓦与金属橡胶串联的空气轴承，建立了理论计算模型，并对其阻尼特性进行了研究[7]。Wilks考虑了瓦块4个自由度的完整动力学模型，但并未考虑温粘效应的影响，只是针对球面接触的可倾瓦轴承进行了动力分析[8]。

国内目前对于挠性支承可倾瓦轴承研究尚处于起步时期，本文借鉴Wilks与复旦大学王丽萍、郑铁生等提出的可倾瓦轴承完整动力学概念与建模思路[10–11]，所不同的是，本文针对目前结构新颖的挠性支承可倾瓦轴承，考虑瓦块摆动与支点移动，油膜区域采用的是考虑了温粘效应影响的二维雷诺方程；根据瓦块支点反力、油膜力平衡方程、轴颈-瓦块运动微分方程，建立其完整动力学仿真模型；通过与相关文献的实验数据进行对比分析，验证理论模型的准确性，为该类型轴承的动力学参数设计提供理论依据。

1 挠性支承可倾瓦完整动力学模型

1.1 瓦块支点反力

瓦块油膜压力合力必然通过支点位置，加上支点为柔性支点，具有一定的弹性，因此挠性支承瓦块具有径向方向（ξk）移动与摆动方向（ΦTilt）的转动自由度。先定义瓦块与壳体之间的反作用力fcξ,k与力矩Mcz,k，这是由瓦块与壳体之间的相对运动引起的。瓦块在径向与切向运动引起的支点径向与切向反作用力以及瓦块摆动所引起的反作用力矩，具体如图2所示。

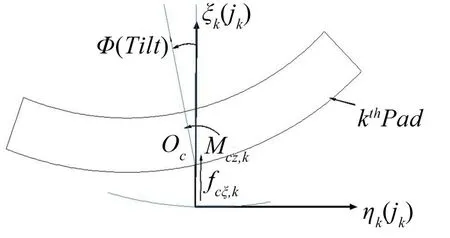
图2 支点反作用力

2 瓦块油膜力、力矩及其刚度阻尼系数［10］

瓦块油膜反作用力通过瓦块表面压力场积分得到，具体如式(1)下所示

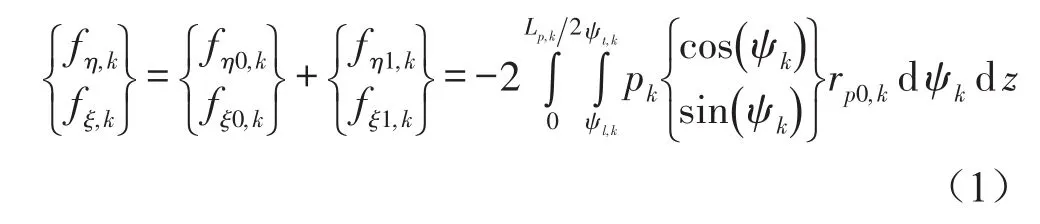
其中fη0,k与fξ0,k是主轴上的反作用力，扰动压力场产生的1阶扰动力为

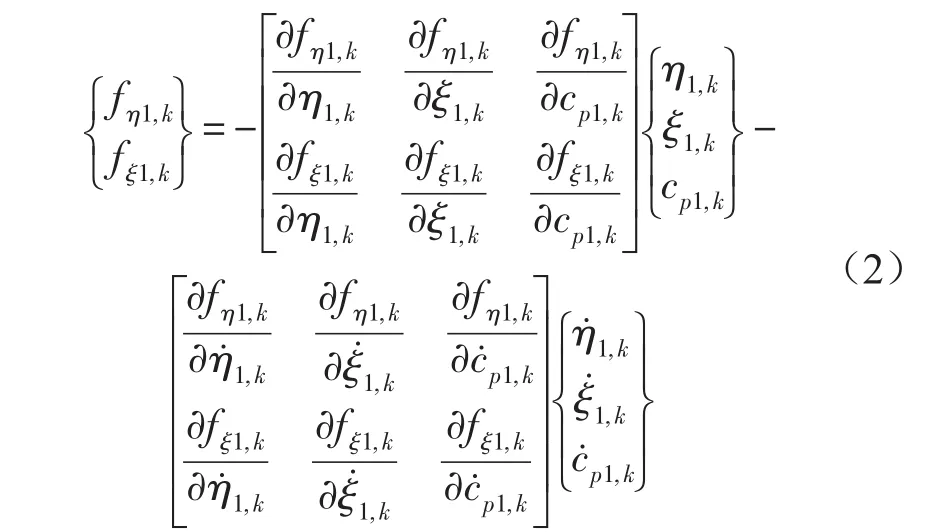
将挠性支承可倾瓦油膜厚度公式代入到式（1）中可以得到

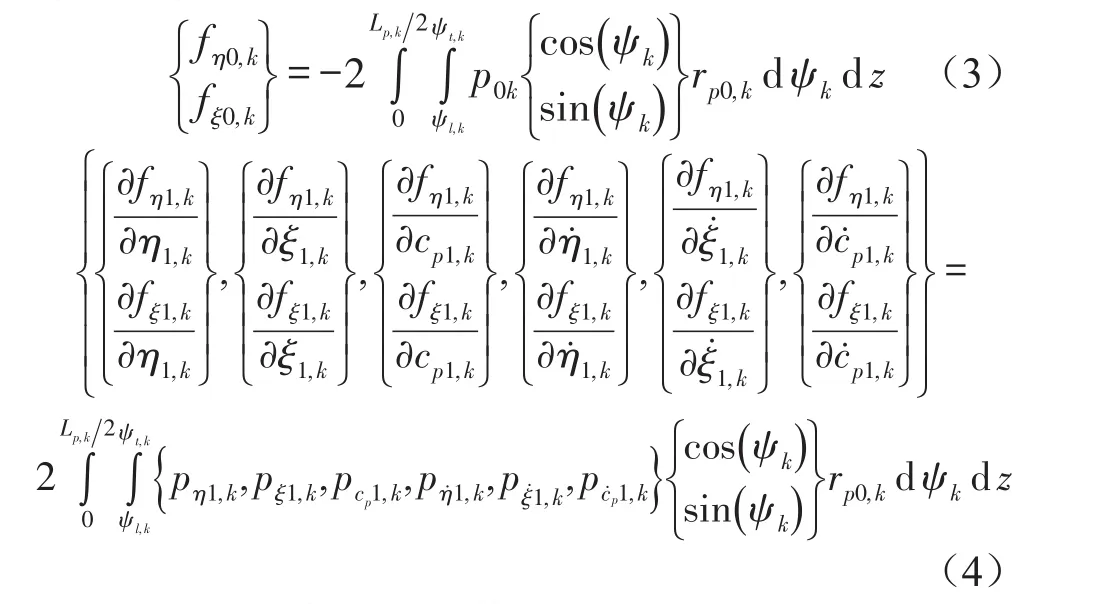
1阶油膜力的偏导数可写成式（4）的形式，该式描述相对于位移和速度扰动的扰动压力场的偏导数。当0阶油膜力与支点反作用力以及轴承载荷平衡时，认为是轴承轴瓦处于平衡位置。因此可以定义平衡位置处转子-瓦块的相对位移以及间隙变化所引起的刚度阻尼系数为

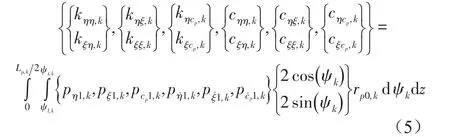
轴承在静态平衡位置的力平衡方程如式（6）所示。其中，第一个方程描述瓦块支点力矩之和，接下来的两个方程描述瓦块切向以及径向方向的力矢量之和。

从图3中可得到瓦块质心相对于参考点即支点Oc的惯性运动方程为

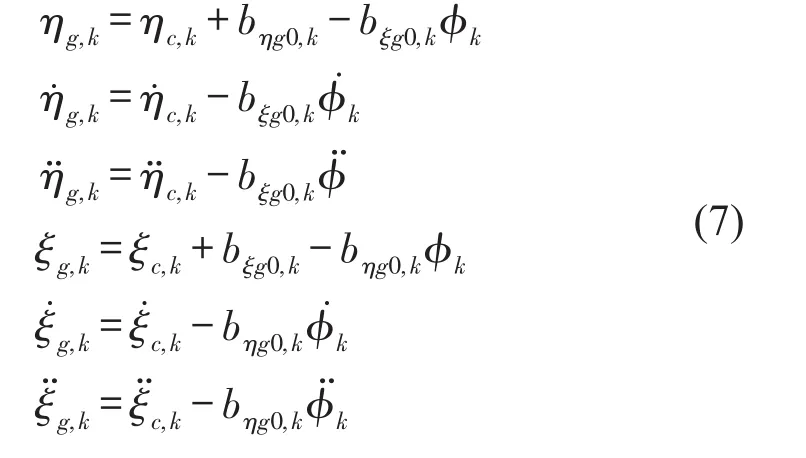
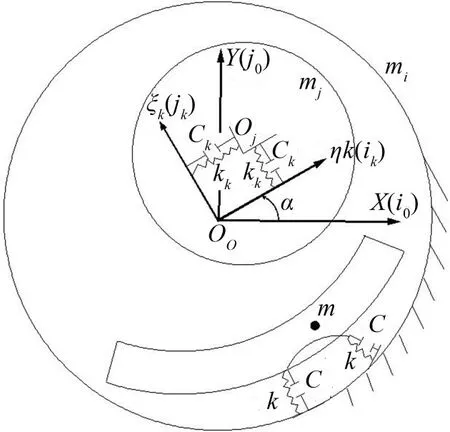
图3 挠性可倾瓦轴承第kth块瓦的动力系数

其中bξg0,k与bηg0,k分别表示在ξ、η坐标上瓦块支点到瓦块质心的间距。

因此可得第kth块瓦的运动方程为

其中第一个方程是瓦块支点偏摆惯性力的总和，另外两个方程分别是瓦块在切向方向与径向方向的力的总和。mp,k是瓦块质量，Ic,k是瓦块相对于支点的惯性矩。

联合轴颈及瓦块运动方程、油膜力方程，可得矩阵形式的方程为

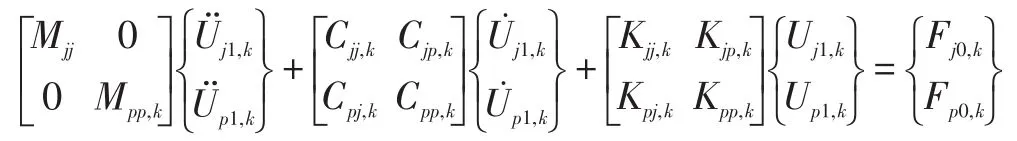
进一步可简写为

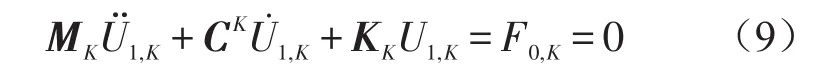
状态向量U1,k表示为

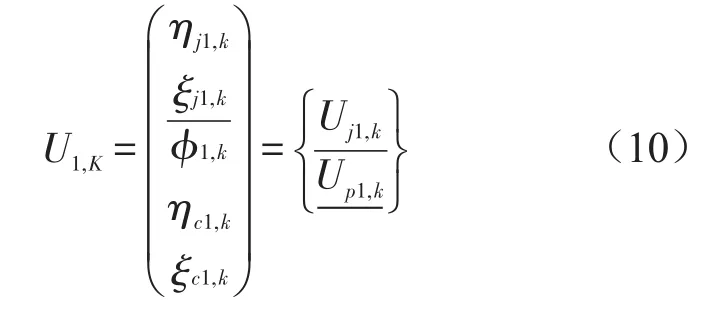
1.3 挠性支承可倾瓦轴承完全动力系数

挠性支承可倾瓦轴承完全动力模型应该是明确包含每个瓦块自由度的动力系统模型，共需要2+2Np方程，其中Np代表在轴承中瓦块的数量。与轴颈运动相关的动力学系数用全局X-Y坐标系来表示，并且每个瓦块将保留其局部参考坐标系ηk-ξk，其支点位置的动力学系数用局部坐标系来表示。完全动力系统的动力学系数矩阵的前两行将留作轴颈运动，而其余2Np行将被分成Np个2组，每组包含瓦块的两个运动自由度因此对于轴颈与挠性支承轴瓦，其完整动力学模型如下所示［10］

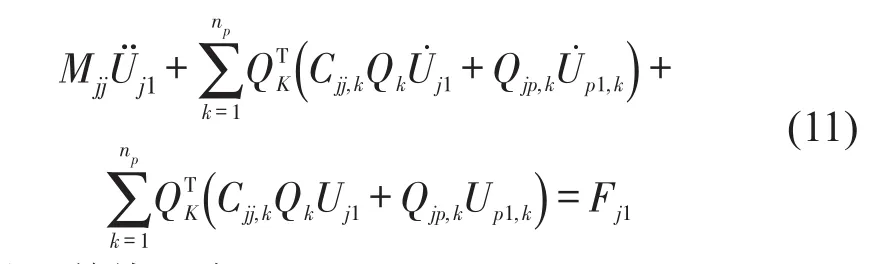
对于单块瓦有

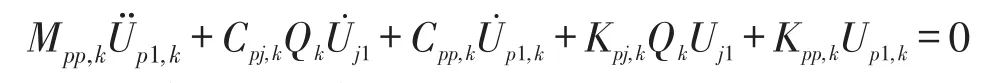
因此可表达为

可将上述挠性支承可倾瓦轴承完整动力学模型与总体坐标系统模型结合，应用于不平衡响应、稳定性分析以及时域瞬态仿真分析。

2 算例分析

2.1 挠性支承可倾瓦轴承参数

采用文献[9]中的四瓦挠性支承可倾瓦轴承进行仿真计算对比，具体轴承工况条件如表1所示。

表1 轴承工况条件

其中四瓦挠性支承可倾瓦轴承的参数具体如表2所示。

挠性支承可倾瓦轴承润滑油牌号为ISO VG32-透平油，其温黏方程为

2.2 分析结果

采用本文提出的完全动力分析模型计算得到四瓦挠性支承可倾瓦径向滑动轴承在不同转速载荷下的完全动力特性系数。对完整动力学模型得到的与轴颈运动相关的动力学系数计算结果与文献[9]中的实验数据进行对比分析，具体如图4、图5所示。

3 结语

考虑动压润滑油膜温粘效应，根据瓦块支点受力的平衡方程、静平衡位置处瓦块油膜力、力矩的平衡方程、瓦块轴颈运动的微分方程，建立挠性支承可倾瓦轴承完整动力学模型，采用本文提出的考虑温粘效应可倾瓦轴承完整动力学模型对挠性支承可倾瓦进行了数值仿真分析，通过与相关文献的试验数据进行对比分析，得出如下结论：

（1）完整动力学模型理论计算结果与实验分析得到的直接刚度系数，都随着载荷的增大呈线性增大趋势，理论计算X与Y方向的直接刚度与阻尼相等（即Kxx=Kyy，Cxx=Cyy），而试验分析得到的X与Y方向直接刚度与阻尼有差异。主要原因为实际工况中由于制造、装配等误差的存在造成了动力特性参数的不对称；且挠性支承可倾瓦轴承中速时完全动力模型计算与实验分析得到的直接刚度与阻尼系数结果较吻合。

（2）完整动力学模型理论计算得到了X、Y方向的交叉刚度系数存在Kyx-Kxy≠0的情况，实验分析结果验证了理论计算模型，说明挠性支承可倾瓦轴承并不具备本质稳定的特点。完整动力学模型理论计算与实验分析得到的交叉阻尼系数较接近，都接近于零。

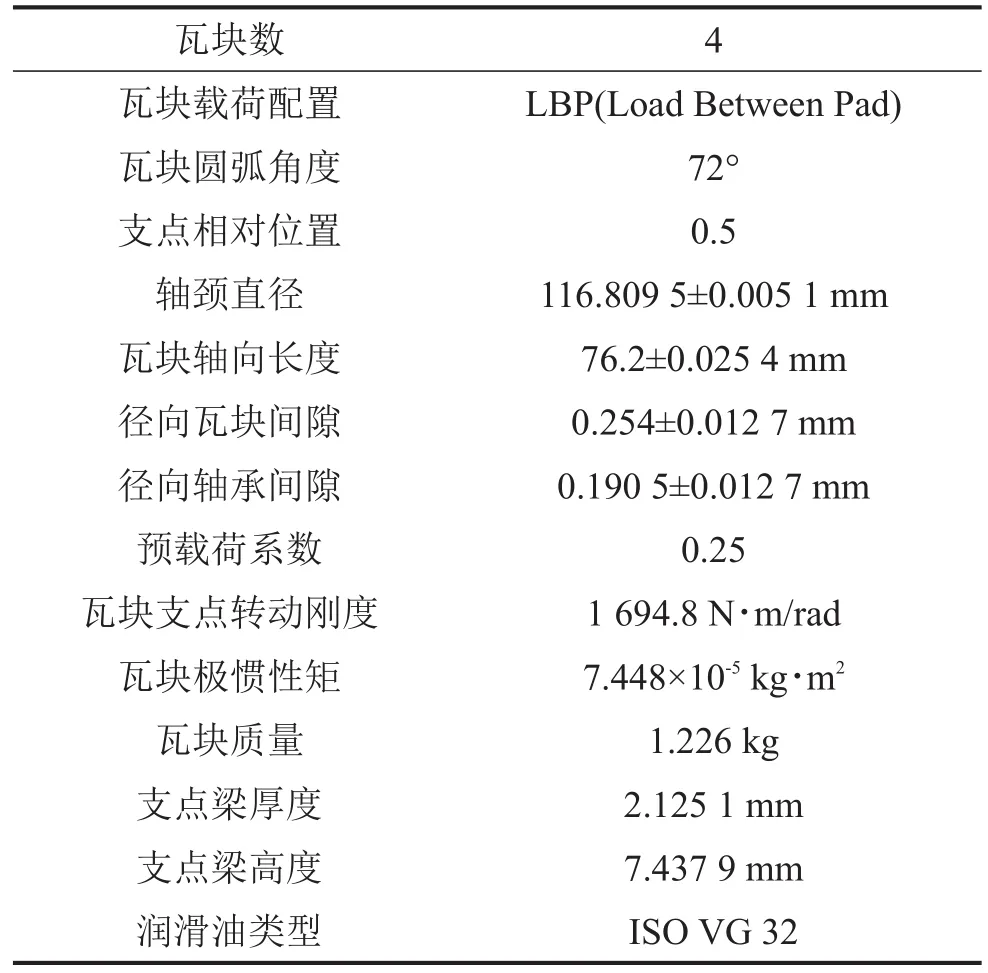
表2 轴承参数表

（3）随着转速的增大，完整动力学模型理论计算与实验分析得到的直接阻尼系数越来越接近，但随着载荷的增大，两者之间的差异也会增大，其主要原因是理论计算中未考虑重载荷下瓦块会产生变形等影响。完整动力学模型理论计算与实验分析得到的交叉阻尼系数较接近，都接近于零。

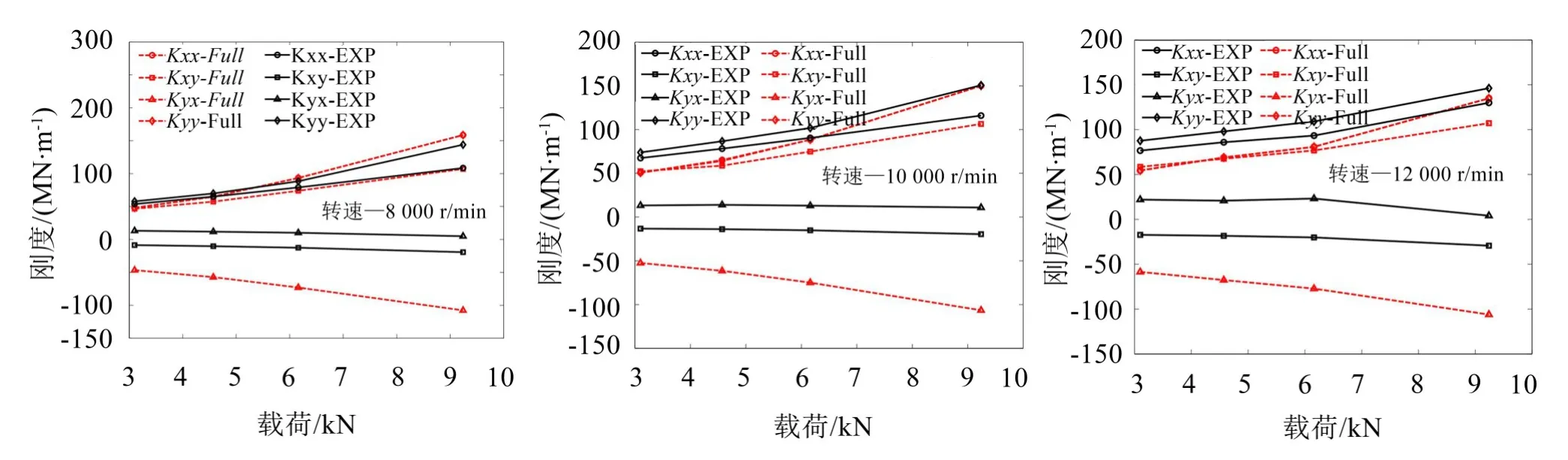
图4 与轴颈运动相关的油膜刚度系数

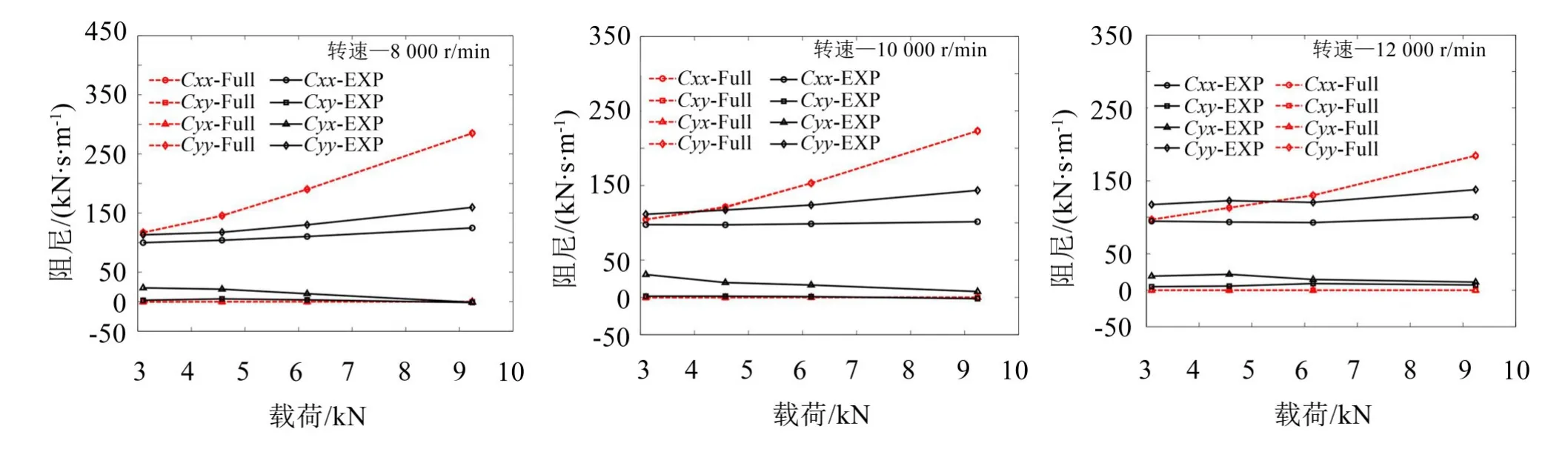
图5 与轴颈运动相关的油膜阻尼系数

综上所述，通过与相关文献的实验数据进行对比分析，验证了本文所提出的挠性支承可倾瓦完整动力学模型的准确性。

[1]ARMENTROUT RICHARD W,PAQUETTE DONALD J.Rotordynamic characteristics of flexure-pivot tilting-pad journal bearings[J].Tribology Transactions,1993,36(3):443-451.

[2]ANDRÉS L S,SANTIAGO O D.Imbalance response of a rotor supported on flexure pivot tilting pad journal bearings in series with integral squeeze film dampers[J].Journal of Engineering for Gas Turbines&Power,2001,125(4):V004T03A023-V004T03A023.

[3]VANCE J,ZEIDAN F,MURPHY B.Machinery Vibration and Rotordynamics[M].Wiley,2010.

[4]SIM K H.Rotordynamic and thermal analyses of compliantflexure pivottilting pad gasbearings[J].Dissertations&Theses-Gradworks,2007.

[5]ADRE′S L S.Hybrid Flexure Pivot-Tilting Pad Gas Bearings: Analysis and Experimental Validation[J].Journal of Tribology,2006,128(3):551-558.

[6]RIMPELA,KIM D.Rotordynamic performance of flexure pivot tilting pad gas bearings with vibration damper[J].Journal of Tribology,2009,131(2).

[7]FENG K,LIU W,ZHANG Z,et al.Theoretical model of flexure pivot tilting pad gas bearings with metal mesh dampers in parallel[J].Tribology International,2016,94:26-38.

[8]WILKES J C,CHILDS D W.Improving tilting-pad journalbearing predictions:partII-comparison of measured and predicted rotor-pad transfer functions for a rocker-pivot tilting-pad journal bearing[J].Journal of Engineering for Gas Turbines&Power,2012,135(1):979-990.

[9]AL-GHASEM A M.Measurement of rotordynamic coefficients for a high-speed flexure pivot tilting-pad bearing(load between pad)configuration[J].Texas A&M University,2006.

[10]WILKES J C,CHILDS D W.Imporoving tilting-pad[A].Journal Bearing Predictions:Part I-Model dvelopment and impact of rotor-excited versus bearing-excited impedance coefficients[C]//ASME Turbo Expo 2012: Turbine Technical Conference and Expositiong,2012:965-978.

[11]王丽萍，乔广，郑铁生.可倾瓦轴承完整动力分析模型及计算方法[J].机械工程学报，2008，44(1)：75-80.

Full Dynamics Modeling andAnalysis of Flexure Pivot Tilting Pad Bearings

YANG Qi-jiang1,2,LI Wei-guang2,ZHAO Xue-zhi2,TENG Xian-bin1
（1.School of Marine Engineering,Guangzhou Maritime University,Guangzhou 510725,China;2.School of Mechanical andAutomotive Engineering,South China University of Technology,Guangzhou 510640,China）

Considering the thermal and viscous effect of lubricating oil film in dynamic compression condition,the geometrical relation between the journal and the tiles is established.The Taylor expansion equations of the zeroth order and the first order for reaction force and moment of the fulcrum are established.The equilibrium equation of the oil film force and moment in the statically equilibrium position is deduced.The kinematic differential equation of the tiles and the journal is proposed.Finally,a full dynamic model of the flexible bearing inclinable pad bearing is established.Solutions of these equations are analyzed and compared with the experimental data in the relevant literatures.And the accuracy of the dynamic model is verified.

vibration and wave;flexure pivot;tilting pad bearings;full dynamic model

TH117.2；TH113.1

A DOI编码10.3969/j.issn.1006-1355.2017.06.002

1006-1355(2017)06-0007-05

2017-03-16

国家高技术研究发展计划863计划资助项目（2015AA043005）；国家自然科学基金资助项目（51375178）

杨期江（1986-），男，博士，湖南省邵阳市人，主要从事涡轮系统减振降噪研究。E-mail:yangqijiang1986@163.com

李伟光（1958-），男，博士，教授，博士生导师，江西省永丰市人，现从事轴承动力学及故障诊断研究。E-mail:wguangli@scut.edu.cn