地铁所致某音乐排练厅室内二次结构噪声测试与仿真

邬玉斌，宋瑞祥，曾钦娥,2，吴 丹，何 蕾，户文成,3

（1.北京市劳动保护科学研究所，北京 100055； 2.北京交通大学，北京 100044；3.北京图声天地科技有限公司，北京 100055）

地铁所致某音乐排练厅室内二次结构噪声测试与仿真

邬玉斌1，宋瑞祥1，曾钦娥1,2，吴 丹1，何 蕾1，户文成1,3

（1.北京市劳动保护科学研究所，北京 100055； 2.北京交通大学，北京 100044；3.北京图声天地科技有限公司，北京 100055）

近年来，随着地铁建设的迅速发展，地铁运行时所产生的振动对邻近建筑室内的二次结构噪声影响逐渐引起人们的关注。为研究室内二次结构噪声数值预测方法，以北京地铁某正线邻近二层音乐排练厅为例，首先对建筑墙、楼板的振动及室内噪声状况进行多点同步详细测试，通过实测数据分析得到地铁运行所致建筑室内振动及二次结构噪声特性；然后采用大型有限元软件Ansys建立隧道-岩土-建筑-声场三维精细化数值仿真模型，对地铁列车通过时的室内二次结构噪声进行仿真计算，并与实测数据进行对比分析。结果表明：地铁列车运行引起的建筑室内二次结构噪声在63 Hz处出现峰值；在100 Hz以下频率范围内仿真结果与实测结果吻合较好；受模型网格划分尺寸影响，100 Hz以上振动和二次结构噪声数值计算结果小于实测值，考虑到地铁运行引起的振动频率主要分布在1 Hz至100 Hz范围内，其对100 Hz以上的振动及二次结构噪声影响相对较小，因此可认为所采用的数值计算方法是科学可靠的，可为类似地铁沿线建筑室内二次结构噪声预测评价提供参考。

声学；地铁；二次结构噪声；现场实测；数值仿真

近年来，随着城市轨道交通的大规模建设，交通线路网不断复杂化、密集化，在人口密集区域内，不可避免会出现地铁线路近距离通过甚至下穿敏感建筑结构的情况。地铁列车在运行过程中所激发的钢轨振动经道床、隧道、土层传递至建筑物基础，最终引起建筑物室内楼板、墙体、梁柱、门窗及家具等的振动，同时向室内辐射噪声。目前国内外的研究多集中于地铁沿线建筑室内振动方面，关于地铁引起建筑室内二次结构噪声的研究较少[1–3]，且主要采用经验公式法预测室内二次结构噪声[2]。而二次结构噪声与地铁列车振动源强和传播路径等诸多因素有关，经验公式法无法准确反映二次结构噪声的特性，且相关测试结果表明，建筑二次结构噪声属于低频噪声[4–5]，对人体产生影响不可忽略。基于此，有必要建立较为准确的模型对地铁引起的建筑室内二次结构噪声特性进行预测。

本文以北京某地铁正线附近某二层音乐排练厅为例，对列车通过时建筑室内墙、楼板的振动和室内噪声进行多点同步测试，同时建立隧道-大地-建筑-声场三维精细化仿真有限元模型，对该排练厅室内二次结构噪声进行预测。该仿真方法可为类似地铁沿线建筑室内二次结构噪声预测提供参考。

1 测试方案与数据分析

1.1 测试方案

测试对象为北京地铁某正线邻近二层音乐排练厅（如图1所示），该建筑距离地铁线路中心线40 m左右，为二层框架结构，建筑层高为4.7 m，分别对一层和二层的排练厅墙体、楼板的振动以及室内噪声进行多点同步现场实测。

图1 建筑室内现场测试照片

其中一层排练厅宽9 m，长13.65 m，二层排练厅宽13.65 m，长18 m。图2为振动测点位置示意图，其中测点1F-Z7和2F-Z7位于室内楼板上，所测方向为垂直地板方向；其余测点均位于室内四周墙壁距离地板约2.35 m高位置处，其中测点1F-X1、1F-X2、1F-X4、1F-X5和2F-X3、2F-X4、2F-X8测量X方向值，即行车方向值；其余测点所测值为Y方向值。

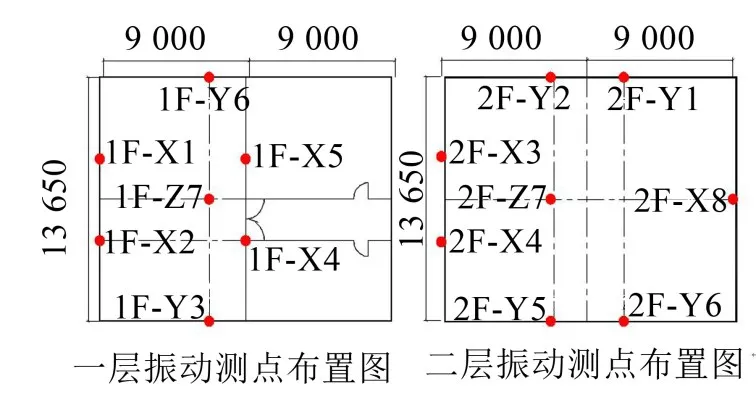
图2 室内振动测点布置图

图3 室内噪声测点布置图

图3为噪声测试位置示意图，测点距离地面高度为1.2 m，可避免人为噪声和其他噪声对测量信号的干扰，测试过程中关闭门窗，室内保持安静[6–8]。

采用数据采集系统同时记录地铁晚高峰时段连续12辆列车通过时室内振动测点的加速度时程和噪声测点的声压时程。

1.2 测试结果分析

1.2.1 室内振动测试结果分析

由于列车通过时室内地板及墙壁处的振动测点的加速度值包含了三个方向，对数据不进行最大Z振级处理，仅做振动加速度级处理，计算12辆列车通过时的实测结果平均值，结果如表1所示。

由表1可知，楼板测点（1F-Z7、2F-Z7）的振动加速度级均大于墙壁测点的振动加速度级，二层楼板测点的振级小于一层楼板测点的振级，平均减小4.8 dB左右。图4为排练厅一层楼板和二层楼板振动加速度级1/3倍频程分布曲线，可见，一层分频振级最大值出现在80 Hz，二层分频振级最大值出现在63 Hz，二层楼板测点的振动在12.5 Hz～40 Hz较强，经分析对应该频率的振动主要由二层楼板固有特性引起。

1.2.2 室内噪声测试结果分析

为分析室内二次结构噪声的频率分布特性，对列车通过时室内噪声声压信号进行1/3倍频程声压级处理，同时计算无列车通过时对应的背景噪声声压级，图5展示了建筑一层和二层室内实测信号与背景噪声1/3倍频程图，可见，在16 Hz～100 Hz频段内，实测噪声值明显大于背景噪声值；在100 Hz以上两者基本重合，说明地铁运行引起的二次结构噪声主要集中在16 Hz～100 Hz频段内。

表1 各室内测点振动加速度级（未计权）/dB

图4 现有排练厅楼板1/3倍频程振动加速度级（未计权）

图6展示室内一层和二层房间室内总实测值与背景噪声值之差的1/3倍频程曲线，可见，在63 Hz～100 Hz范围内，实测值与背景噪声声压级之差最大，约在6 dB以上，峰值出现在63 Hz和80 Hz处，这与室内振动测试结果一致，说明该噪声值主要由建筑结构的振动产生。而在16 Hz～63 Hz范围内，实测值与背景噪声声压级之差在0.5 dB～3 dB内。

2 三维数值仿真模型

2.1 声学波动方程

建立数值仿真模型对声场进行流固耦合分析时，综合考虑结构的动力方程与Navier-Stokes方程的动量方程和连续性方程。声学基本方程是流体方程把空气作为特殊流体条件下的简化。对理想流体介质做以下假设：

(1)流体是可压缩的，密度随压力变化而变化；

(2)流体是非粘性流体，忽略粘性引起的能量损耗；

(3)流体中没有不规则流动；

(4)流体是均质的，各点平均密度和声压相同。

流体的动量方程（Navier-Stokes方程）和连续性方程可以简化为声场波动方程

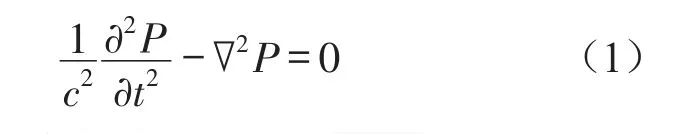
c为流体介质中的声速，其中ρ0为流体密度，k为流体体积模量；P为声压；t为时间。

综合考虑离散化的结构方程和无损耗的波动方程，将界面S处流体声压荷载加入结构有限元方程中得到

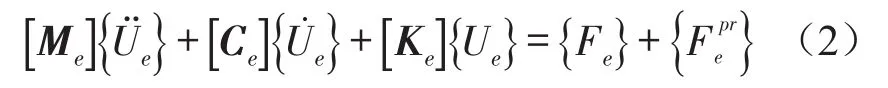
2.2 有限元模型建立

采用大型有限元软件Ansys根据上述测试对象建立隧道-土体-建筑-声场三维仿真模型，模型如图7所示，利用建筑物室外地表振动实测数据对计算模型参数进行调整、校核、验算，进而计算分析该建筑室内二次结构噪声，计算结果与实测结果进行对比分析。

模型包括隧道、岩土、建筑及空气单元，模型长、宽、高为139.89 m×79 m×35 m，模型约含26.0万个单元，其中声学单元有16.1万个，节点约有12.1万个，网格尺寸为2 m。模型中土体、隧道、轨道部分采用SOLID45模拟，建筑中梁、柱采用梁单元BEAM188模拟，墙体、楼板采用SHELL63单元模拟。

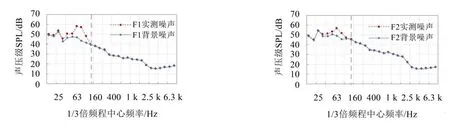
图5 建筑室内实测噪声与背景噪声1/3倍频程曲线

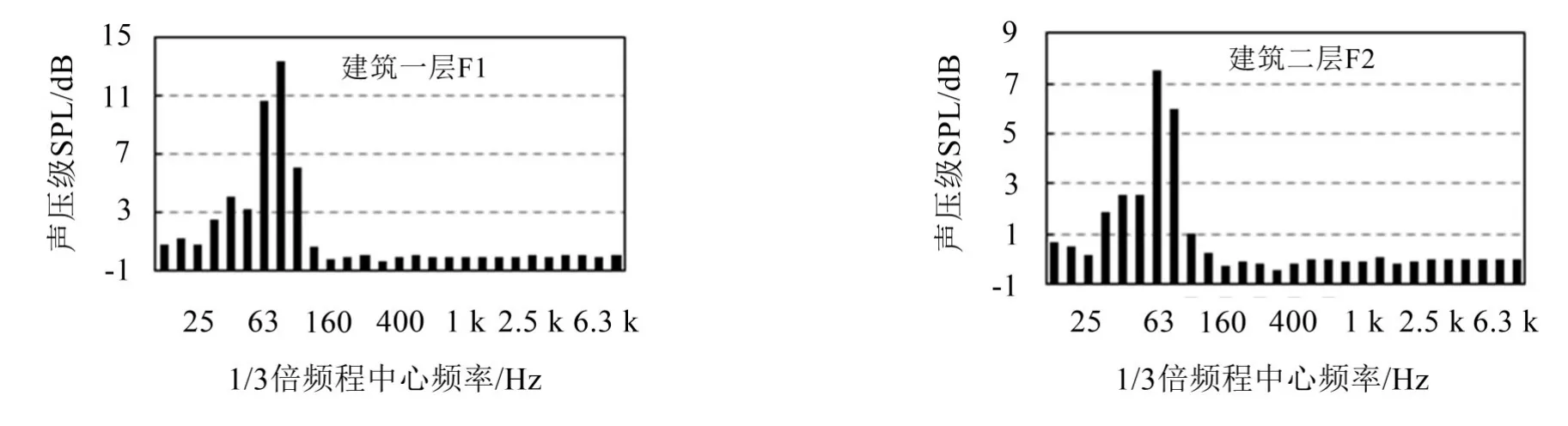
图6 建筑室内噪声实测值与背景噪声值之差分布

图7 隧道-土体-建筑-声场三维有限元模型

采用黏弹性人工边界条件消除反射波的计算影响。通过在人工截断的边界上设置连续分布的并联弹簧-阻尼器系统来等效模拟，其中弹簧元件的弹性系数Kb及黏性阻尼器的阻尼系数Cb的计算公式如下[9]

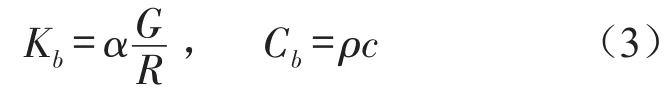
式中ρ和G分别表示介质的质量密度和剪切模量;R表示波源至人工边界的距离；c表示介质中的波速，法向人工边界波速取纵波波速，切向人工边界波速取剪切波波速；参数α根据人工边界的类型及设置方向取值。

根据地质资料，将土层划分为五层，每层土体的埋深及物理材料参数见表3。地铁隧道中心线埋深为20.87 m，对近距离隧道列车行驶对建筑结构的振动影响进行数值计算分析。隧道壁、轨道、建筑结构和墙体材料均采用强度为C35的混凝土。

利用有限元软件Ansys可以对声学和流体-结构相互作用进行分析，声学单元Fluid30可以模拟室内空气的流动。图8所示为结构-流体有限元模型，内部空气单元采用只有一个自由度（声压）的Fluid30模拟，与墙体接触的空气单元采用具有四个自由度（三个方向的位移及声压）的Fluid30进行模拟，在流体与建筑楼板和墙体接触面采用流固耦合界面（FSI）。

通过此模型可以计算四周墙体振动所辐射的声压值，模型中未考虑建筑墙体的反射和吸声系数，且实际建筑楼板为木质地板，模型中未考虑。

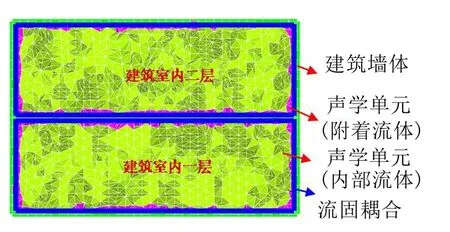
图8 建筑室内声场有限元模型

3 计算结果分析

3.1 模型校核

由于无法获取隧道内部真实的列车源强振动数据，本文根据列车轴重、车轮个数、轴间距等列车实际参数，结合场地土实测地铁振动频谱特性，构建由不同频率正弦力组合而成的列车激振力，并采用考虑列车运行速度的移动列车荷载输入方法，图9为本文模型中车轮激振力时程曲线。

采用上述有限元模型和列车荷载激振力模拟计算地铁通过对场地土的振动影响，并与场地土实测数据进行对比验证。

为验证该数值仿真模型的计算精度，利用建筑附近室外场地土测点作为模型校核点对模型计算参数进行调整、校核，校核点距离近轨隧道中心线为25 m，校核点与隧道、建筑物的相对位置关系如图10所示。

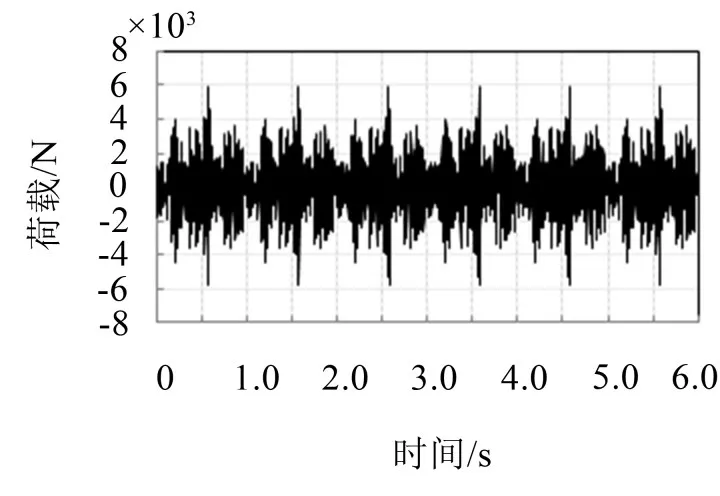
图9 轮轨激振力时程曲线

现场实测值与计算值振动加速度级（未计权）分别为93.31 dB和92.58 dB，差值仅为0.79 dB。进一步将计算与实测加速度频谱进行对比(见图10)，可以看出在1 Hz～80 Hz范围内幅值和频谱分布规律基本一致，仅在71 Hz左右数值计算值大于实测值。因此，该数值模型计算精度满足模型校核要求。

表3 土层物理参数

图10 校核点与建筑相对位置图

图11 校核点实测值与计算值频谱对比图

3.2 室内噪声分析

利用上述模型对地铁运行引起的室内二次结构噪声声压进行计算，并做线性声压级处理，将计算结果与实测结果进行对比，如图12所示。

从图中可以看出，在100 Hz以下，两者频率分布趋势较为一致，均在63 Hz处出现最大值，计算结果略大于实测值，这主要是由于计算模型未考虑室内四壁的吸声系数；在100 Hz以上，实测结果显著大于仿真结果，计算值呈迅速下降趋势，这主要是由于受计算机计算效率的影响，仿真模型网格尺寸划分较大，无法有效模拟高频范围的振动。而实测结果表明地铁引起的室内二次结构噪声影响主要集中在16 Hz～100 Hz范围内，因此采用该数值仿真方法计算地铁引起的室内二次结构噪声具有一定的可靠性。

3.3 室内二次结构噪声分布特点

为分析室内不同空间位置处的二次结构噪声，提取一层排练厅室内不同空间位置处的声压级数据进行计算，图13(a)为噪声提取点平面位置示意图，其中拾取点1-9位于房间正中心处，拾取点1-1、1-4、1-14、1-17空间位置相互对称。为分析同一位置不同高度的声场分布情况，分别提取距离楼板1 m、2.35 m、4 m处三个不同高度处的声压，计算结果如图13(d)所示。图13(b)为高度H=2.35 m处相互对称位置的拾取点声压级，可见4个拾取点的噪声值频率分布趋势基本一致，各拾取点的最大差值约2 dB左右，因此空间对称位置处的声压级差异较小。图13(c)为高度H=2.35 m处不同位置拾取点的声压级，四个点距四周墙壁的距离由远及近分别为1-9、1-6、1-2、1-1，可见，除个别频率外，距离各墙壁最远中心位置的拾取点1-9的噪声值最小，其次为点1-6；而点1-1与1-2两者相比，在50 Hz以下，点1-1的噪声值略大，而在50 Hz以上，点1-1的噪声反而比点1-2的值小。图13(d)为不同频率、不同高度处相同位置拾取点的声压级，可得，在中心频率25 Hz～50 Hz范围内，高度H=2.35 m处拾取点的声压级位于H=1 m和H=4 m两者声压级之间，而其他频率范围内，高度H=2.3 5m处的噪声值最小。

4 结语

对北京地铁正线沿线附近某二层音乐厅室内振动和二次结构噪声特性进行现场测试和数值计算分析。实测结果表明，地铁振动引起的音乐厅楼板的振动峰值出现在63 Hz和80 Hz处，地板垂向振动大于墙体水平振动，其中一层楼板处的振动加速度级比二层的大4.8 dB左右。地铁列车通过对本音乐排练厅室内二次结构噪声影响主要集中在16 Hz～100 Hz频率范围内。

图12 一层和二层室内中心位置处二次结构噪声声压值

图13 不同空间位置处室内二次结构噪声

本文建立隧道-岩土-建筑-空气精细化室内二次结构噪声数值仿真模型，计算室内二次结构噪声，与实测结果的对比分析表明，在100 Hz以下，仿真结果与实测结果趋势上较为一致，而在100 Hz以上，实测结果明显大于仿真预测结果，计算结果迅速减小，这主要是由于仿真有限元网格尺寸受到计算机计算效率的限制，无法有效模拟高频范围（100 Hz以上）的振动，同时由于仿真模型中未考虑墙面反射及吸声作用，室内二次噪声计算值与实测值幅值差别较大。实测结果表明，地铁列车通过引起的振动和室内二次结构噪声频率范围主要集中在100 Hz内，因此可以认为该数值方法计算地铁引起的该建筑物室内二次结构噪声是可行的。

通过分析不同空间位置处二次结构噪声分布特点可以发现，空间相对称位置处噪声值较为一致，差值在2 dB以内；另外，除个别频率外，拾取点位置距离墙壁及楼板越远，噪声值越小，但差值均较小，这可能与文中未考虑墙面反射及吸声作用有关。在实际应用过程中，为更加有效模拟地铁列车引起的室内二次结构噪声，需要进一步解决模型网格尺寸与计算效率之间关系的问题以及考虑建筑物室内反射及吸声作用。

[1]唐娟.地铁列车运行引起的建筑物内结构噪声研究[D].南昌：华东交通大学，2013.

[2]康波.地铁上方建筑物振动级二次噪声辐射分析[D].成都：西南交通大学，2008.

[3]杨碧君，张硕.地铁运行引起室内结构噪声的评价指标研究[J].声学技术，2010，29(2)：264-265.

[4]申道明，张来栋.地铁引起二次噪声特性及评价量实测与探讨[J].土木建筑与环境工程，2013，35(4)：133-136.

[5]储益萍.地铁引起的结构振动与噪声及其相关性分析[J].噪声与振动控制，2011，31(4)：85-88.

[6]中华人民共和国住房和城乡建设部.JGJ/T 170-2009城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准[S].北京：中国建筑工业出版社，2009.

[7]国家环境保护局.GB 10070-1988城市区域环境振动标准[S].1988.

[8]国家环境保护局.GB 10071-1988 城市区域环境振动测量方法[S].1988.

[9]刘晶波，王振宇，杜修力.波动问题中的三维时域黏弹性人工边界[J].工程力学，2005，22(6)：46-49.

Test and SimulationAnalysis of Ground-borne Noise in a Rehearsal Hall Caused by Subway Operation

WU Yu-bin1,SONG Rui-xiang1,ZENG Qin-e1,2,WU Dan1,HE Lei1,HU Wen-cheng1,3
(1.Beijing Municipal Institute of Labour Protection,Beijing 100055,China;2.BeiJing Jiaotong University,Beijing 100044,China;3.Beijing NV&M Technology Co.Ltd.,Beijing 100055,China)

With the rapid development of rail transportation,the ground-borne noise induced by passing-by trains in subways has been attracting serious public attentions.In this paper,the numerical simulation method for prediction of the ground-borne noise is studied with a rehearsal room beside two subway lines in Beijing as an example.First of all,a series of vibration tests on the structural floors and walls is conducted,and the sound pressure at the room center is measured.The characteristics of the vibration and the ground-borne noise caused by subway trains are summarized.Then,a tunnel-soilstructure coupled 3D finite element model of is established by means of Ansys to simulate the ground-borne noise.The results are compared with the test data.It shows that the numerical result agrees well with the test result below 100 Hz,and the peak of the ground-borne noise is found at 63 Hz in both results.Above 100 Hz,however,the simulation result is smaller than the test result due to the influence of the mesh size.Since frequency of the vibration caused by passing-by trains is usually in the range of 1-100 Hz,the simulation result is considered to be appropriate and sufficiently accurate.The proposed model provides a reference for similar cases in the prediction of the ground-borne noise induced by passing-by trains in subways.

acoustics;subway;ground-borne noise;in-situ test;numerical simulation

T112.3；TU311.3

A

10.3969/j.issn.1006-1355.2017.06.025

1006-1355(2017)06-0120-06

2016-12-12

2016年北京市财政资助项目(PXM2016_178304_000011)

曾钦娥(1990-)，女，江西省宜春市人，硕士，主要研究方向为环境振动与噪声。E-mail:250295064@qq.com