基于高维模型的客车发动机悬置系统NVH性能优化

李伟平，尹文锋，曾亮铭，杨玉清，毛光军

（湖南大学 汽车车身先进制造国家重点实验室，长沙 410082）

基于高维模型的客车发动机悬置系统NVH性能优化

李伟平，尹文锋，曾亮铭，杨玉清，毛光军

（湖南大学 汽车车身先进制造国家重点实验室，长沙 410082）

汽车NVH性能是衡量汽车乘坐舒适性的重要指标，其噪声声压级高低和振动幅值大小直接影响乘员的主观感受。通过怠速时整车NVH测试，确定动力总成悬置系统对驾驶员座椅处NVH性能影响最大。选取动力总成四点悬置处刚度和阻尼作为设计变量，利用基于薄板样条插值函数的高维模型（TPS-HDMR）构建设计变量与目标函数之间的近似模型。以驾驶员座椅处振动幅值为约束条件，采用遗传算法对驾驶员右耳处声压级进行优化，优化结果表明客车NVH性能得到明显提升，验证了该方法的可行性。

振动与波；NVH测试试验；悬置系统；薄板样条插值函数；近似模型；遗传算法

汽车车内噪声直接影响汽车乘坐舒适性，也是汽车质量评价的标准之一。发动机动力总成系统是汽车振动噪声来源的重要部分。为了降低发动机的振动，大量采用隔振、降噪的悬置元件，而悬置元件参数选取一直是发动机隔振研究的热点问题[1]。

近年来对这方面问题有不少研究，杨明亮等提出利用响应面法得到车内噪声与动力总成悬置系统特性参数定量关系的响应面模型，进而建立动力总成悬置系统声学优化模型[2]；温任林等建立15自由度的力学模型[3]，建立以汽车驾驶室振动能量最小和发动机悬置能量解耦为综合目标的多目标优化模型，对发动机悬置参数进行了优化，优化效果较好。

近年来为了提高计算效率，应用响应面法、Kriging插值等近似方法处理低维和非线性程度不高的问题取得了很好的效果。而对于复杂的非线性模型，随着维数和非线性程度的增加，构造近似模型所需的样本点数量和计算花费呈指数增长，计算效率大大降低。高维模型可以将计算时间和效率随维数或非线性程度呈指数级增长的隐函数，转换成可以忽略高阶耦合项的多项式函数，从而节省了计算时间，在处理非线性高维问题时优势明显[4–6]。

本文针对某中型客车怠速噪声过大的问题，进行客车NVH试验与分析，找出原因。以发动机四点悬置处的刚度和阻尼为设计变量，驾驶员右耳处声压级与座椅处振动均方根值为目标，建立基于TPSHDMR的高维近似模型。运用遗传算法对其动力总成四点悬置处的弹性元件特性参数进行优化和设计。

1 整车怠速时NVH试验及分析

某型号客车在怠速转速为700 r/min～800 r/min时，车体产生强烈的振动，车内的噪声较大，客车的乘坐舒适性降低。通过对整车进行NVH测试，分析振动产生原因。

1.1 客车NVH性能测试及测点布置

整车NVH性能测试测点布置：振动测点12处、噪音测点11处。如图1、图2所示。

图1 实际振动测试点布置

图2 实际噪声测试点布置

1.2 客车NVH性能测试结果及分析

根据客车怠速时出现的振动问题，测量空调关闭条件下不同转速n（600、700、800、900、1 000、1 100、1 200）下的振动和噪声信号。通过信号采集分析来准确了解整车的噪声和振动特性，测试结果如图3、图4所示。

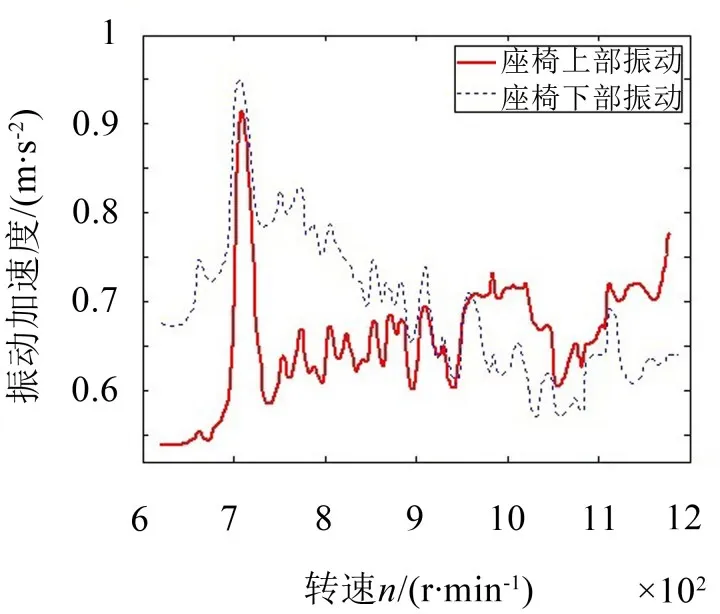
图3 怠速时座椅处振动测试结果

图4 整车内部噪声测试结果

从图3、图4分析可知，该型号客车的NVH性能在怠速转速在700 r/min～800 r/min之间急剧变差，且达到峰值，与主观评价相符合。

车辆怠速工况下，车辆噪声源会出现明显的阶次现象，即发动机凸轮轴运动引起的与转速相关的振动与噪声，与发动机冲程数量和缸数相关。发动机振动的激励频率主要为发动机气缸内点火燃烧、曲轴输出脉冲扭矩引起的激励频率，其大小为

式中n为发动机转速(r/min)；

i为缸数；τ为冲程系数；

f为发动机激励频率(Hz)。

该试验客车的发动机为直列四缸四冲程柴油发动机，根据上式计算得750 r/min怠速工况下发动机振动激频为12.5 Hz，则第2阶为25 Hz，第4阶、第6阶以此类推。该车在怠速（750 r/min左右）工况下车内振动1/3倍频程分析和阶次分析结果如图5至图7所示。

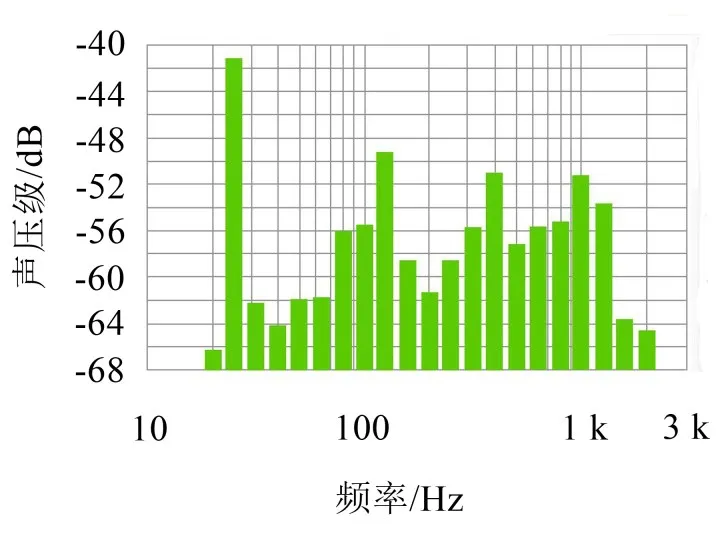
图5 怠速时驾驶员座椅上1/3倍频程振动图

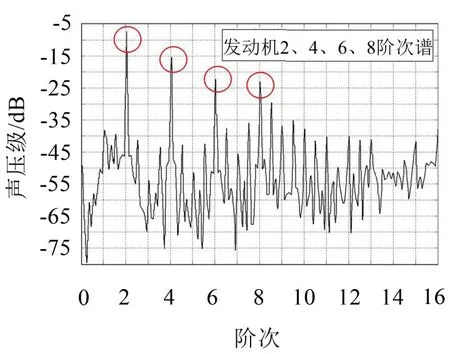
图6 怠速时驾驶员座椅上振动阶次图

图7 怠速时驾驶员座椅上振动阶次跟踪占比图

由图5、图6、图7分析可知，该工况下振动激励主要来自发动机，数据分布整体呈现阶次状态，“高峰”为发动机各阶振动频率造成的。第2阶（25 Hz）的影响最大，且占主导地位，其后随着阶次升高影响依次下降。在怠速（750 r/min）工况下，车内噪声振动在25 Hz附近处的幅值有明显增大，对车内NVH性能影响最大，进一步验证了客车在转速为700 r/min～800 r/min之间时会出现振动噪音较大的问题。

1.3 驾驶员座椅振动传递路径分析

由于激励力的测量受到动力总成空间的限制，试验时在发动机四点悬置处和驾驶员座椅上布置振动加速度传感器。分别测量发动机输入的振动激励和通过发动机悬置传递到座椅上的振动。最后计算得到发动机四点悬置与驾驶员座椅的振动传递函数表达式如下[7]

式中

i为发动机悬置点（i=1～4）；

Hi为第i个发动机悬置振动传递函数；

Ai,seat为第i个发动机悬置所对应的主驾驶员座椅处加速度值；

Ai,mount为第i个发动机悬置处的加速度值。

根据测量计算，怠速（转速为750 r/min左右）时发动机四点悬置与驾驶员座椅的振动传递函数曲线如图8至图11所示。

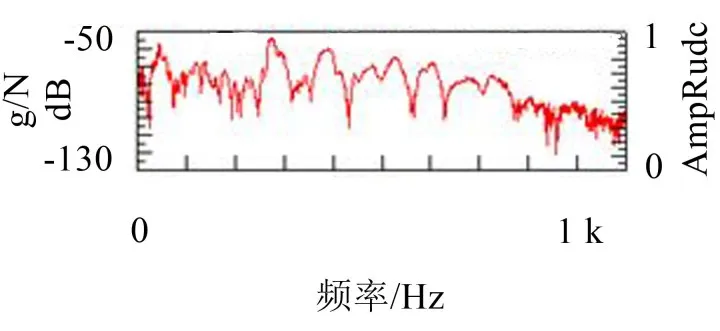
图8 右前悬置处与驾驶员座椅振动传递函数

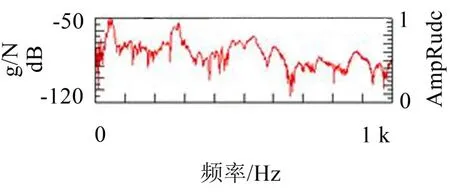
图9 右后悬置处与驾驶员座椅振动传递函数

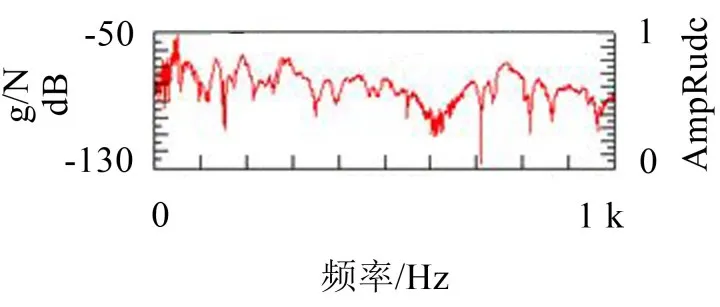
图10 左前悬置处与驾驶员座椅振动传递函数

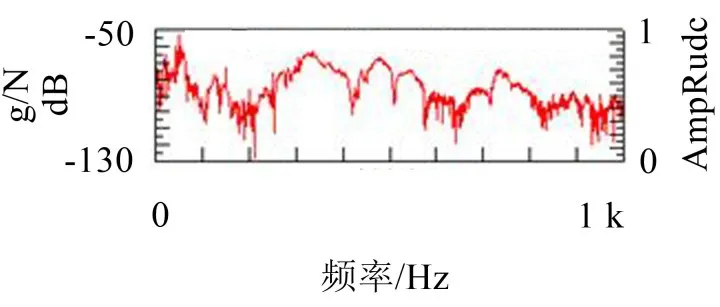
图11 左后悬置处与驾驶员座椅振动传递函数

由图8、图9、图10、图11可知：在发动机二阶激励频率段四点悬置激励所致的发动机的振动的衰减效果变差，而在其他频率段内衰减效果相对较好。因此该客车在怠速状况下车内噪声振动问题主要是由发动机悬置系统设计匹配不合理引起的。为解决这一问题，本文优化发动机悬置系统弹性元件特性参数，以提高客车整车的NVH性能。

2 客车声-固耦合系统建模仿真

2.1 车身有限元模型的建立与验证

本文利用HyperMesh建立车身各部件的有限元模型。模型相关参数如下：

网格大小为20 mm，材料密度为7.8 g/cm3，弹性模量为2.1×105Mpa，泊松比为0.3，整个车身模型有580 559个节点、575 636个壳单元和42 578个六面体单元。模型如图12所示。

图12 客车车身有限元模型

计算该车身在0～100 Hz之间的模态，并对车身进行模态试验。计算模态和试验模态的结果对比见表1。由表1可知，试验模态和计算模态的频率偏差在5%之内，验证了车身有限元模型准确性。

2.2 声-固耦合模型建立

建立车身内部声腔网格。根据每个声波波长至少含有6个声学单元的原则，结合本文的计算频率（20 Hz～200 Hz），取声学单元网格的长度为100 mm。声固耦合模型见图13，模型的相关参数如下：

图13 客车内部声腔网格模型

单元总数量为180 560个（其中90%以上为四面体单元），节点总数为186 571个；空气密度为1.29 kg/m3；体积模量为 141.6 kN/m2。

将客车声振模型导入LMS.Virtual.Lab中进行声振耦合分析，得到怠速工况下发动机悬置特性参数不同时的驾驶员右耳处声压值。

由于怠速状态下，客车座椅导轨处的振动来自于发动机振动向车身传递的结构振动激励。本文利用LMS Test.Lab软件直接测量发动机四点悬置处的激励，将采集的时域信号进行A/D和FFT变换，转化为频域信号，最后将激励的频域信号加在发动机四点悬置处，在Hyper Works软件中求出客车座椅处的振动响应。

3 发动机悬置系统高维模型建立

3.1 设计变量选取

发动机悬置共有4个橡胶元件，其中2个连接发动机和发动机支架（副车架），另外2个连接发动机和车身。本文选取发动机4点悬置处橡胶元件刚度和阻尼为设计变量，驾驶员右耳处声压级和驾驶员座椅振动均方根值为目标，建立悬置系统高维模型。8个设计变量如下：

x1、x5为发动机前部与发动机支架连接橡胶件的刚度和阻尼；

x2、x6为发动机后部与发动机支架连接橡胶件的刚度和阻尼；

x3、x7为发动机前部与车身连接橡胶件的刚度和阻尼；

x4、x8为发动机后部与车身连接橡胶件的刚度和阻尼；

各设计变量取值范围如表2所示。

3.2 高维模型构建

本文选择TPS-HDMR方法来构建客车悬置系统弹性元件特性参数与驾驶员右耳处声压级及驾驶员座椅振动均方根值的近似模型，其构建优化目标响应近似模型的具体步骤如下[8]：

(1)选取中心点X0=[x1,x2,…,x8]，计算该样本点的发动机四点悬置弹性元件特性参数与驾驶员右耳处声压级响应值f0。

（2）构建每个设计变量xi的薄板样条近似函数

（3）得到TPS近似模型

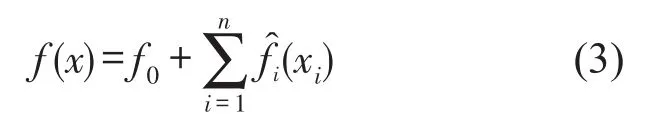
表1 车身试验模态与计算模态的对比

表2 各优化变量取值范围

（4）判断TPS近似模型精度：在设计变量空间内，运用拉丁超立方实验设计方法随机选取5个采样点。分别对真实模型和近似模型进行计算，并计算两者的相对误差。若相对误差满足给定精度要求（设定为5%），那么构建近似模型成功，如果精度不满足要求，则继续执行第5步。

（5）检测每对设计变量xi、xj的相关性，构造近似函数代入式(3)得到近似函数模型

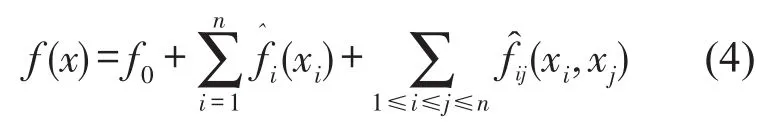
再转到第4步，进行精度判断，如果满足精度要求则程序停止。若依然不满足精度要求，则继续计算更高阶的耦合项，直至满足精度的要求。

（6）式(4)为构建的客车发动机4点悬置处刚度、阻尼与驾驶员右耳处声压级的近似响应函数，其与驾驶员座椅处振动幅值近似响应函数的建立也是同理。

对每个设计变量在其取值范围内等间距取点，取点数量根据构建近似模型时是否达到预先设定的精度（5%）决定。TPS-HDMR构建近似模型过程中总共计算了48个样本点得到满足工程要求的近似模型。本文利用拉丁超立试验设计方法选取的5个样本点验证TPS-HDMR近似模型的精度。由表3和表4可知，真实值与近似模型值的相对误差小于5%，验证了模型的正确性。

表3 怠速工况下发动机2阶频（25 Hz）时基于近似模型的驾驶员右耳处声压值响应精度判断（A计权）

表4 怠速工况下发动机2阶频（25 Hz）时基于近似模型的驾驶员座椅处振动值响应精度判断（Z方向，单位g）

4 悬置参数优化

4.1 目标函数的建立

在发动机悬置参数优化设计中，以驾驶员座椅处振动加速度均方根为约束条件，以车内驾驶员右耳处声压等级最小为目标[9–10]，车内噪声单目标优化模型可以描述为

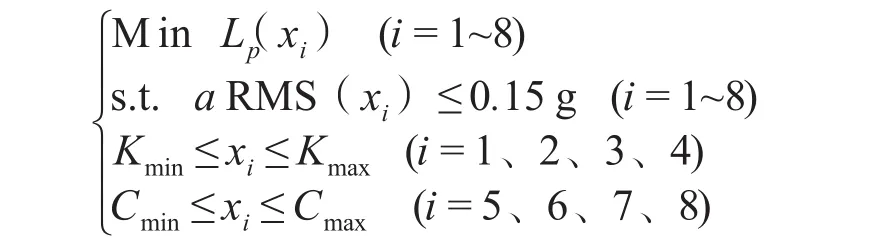
式中

Lp为怠速状态下发动机2阶频（25 Hz）时客车驾驶员右耳处声压级(dB)；

aRMS为怠速状态下发动机2阶频（25 Hz）时客车座椅处振动加速度均方根值(m/s2)；K为客车发动机四点悬置刚度的上下限值；C为客车发动机四点悬置阻尼的上下限值。

4.2 优化过程及分析结果

将加入精英保持策略和遗传算法结合起来，在客车驾驶员右耳处声压级和驾驶员座椅处振动加速度均方根值的TPS-HDMR近似模型的基础上，求解客车发动机四点悬置参数优化问题。优化过程中种群数设置为100，经过200次迭代，交叉概率0.9，变异概率0.1。优化设计前后设计变量如表5所示。

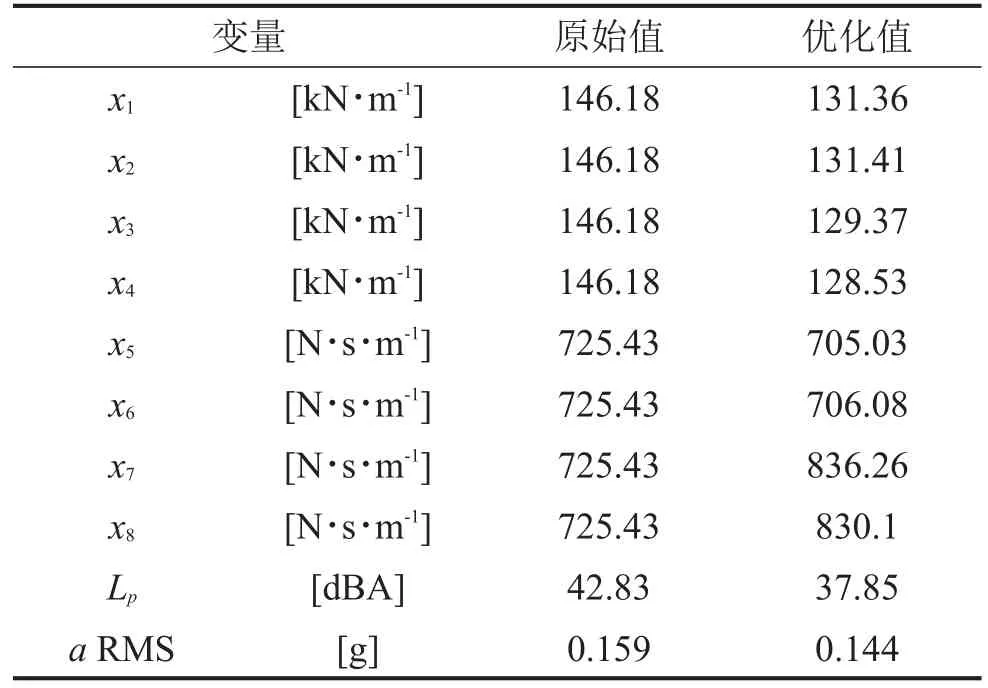
表5 发动机四点悬置刚度阻尼优化前后数据对比

把优化结果代入有限元模型，计算得客车怠速工况下驾驶员右耳处声压级和驾驶员座椅处的振动幅值，优化前后结果对比如图14和图15所示。

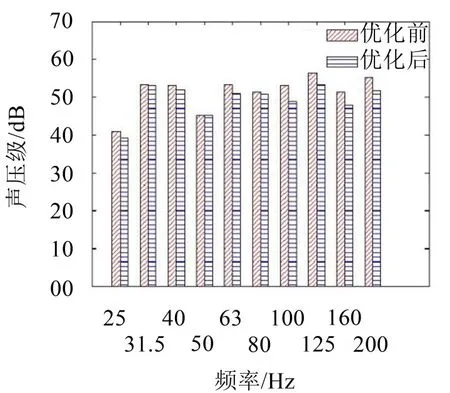
图14 怠速工况下驾驶员右耳处1/3倍频程声压级对比

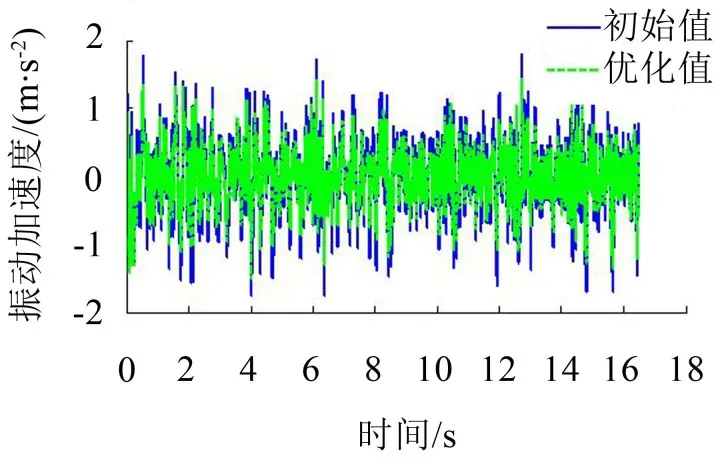
图15 怠速工况下驾驶员座椅处振动幅值时域对比

根据图14、图15可知，优化前后驾驶员右耳处声压级和驾驶员座椅处振动幅值均有较明显降低。由表5知，发动机2阶频（25 Hz）时，声压级降低将近5.0 dB，降低率约为11.6%，而振动幅值降低0.015 g，降低率约为9.4%。

5 结语

在发动机悬置系统设计时，应选取恰当的悬置刚度和适当的阻尼使悬置系统的固有频率避开整车各子系统的固有频率以免发生共振。本文首先通过试验确定客车怠速时噪声主要来自发动机。接着对客车进行声-固耦合系统建模仿真。以发动机悬置参数为设计变量，用TPS-HDMR构建了设计变量与目标函数之间的近似模型，以代替优化计算时调用的真实有限元模型。对发动机悬置参数进行优化，并对比了优化前后客车内部驾驶员右耳处声压级和座椅处振动幅值，结果表明客车NVH性能有了明显的提升，证明所采用的方法具有一定的理论和工程实际意义。

[1]毛光军.基于高维模型的客车动力悬置系统NVH性能优化研究[D].长沙：湖南大学，2016.

[2]李锐，陈伟民，廖昌荣，等.发动机橡胶悬置特性的试验与建模研究[J].中国机械工程，2009，20(22)：2746-2750.

[3]杨明亮.汽车动力总成悬置系统NVH性能分析及改进设计[D].成都：西南交通大学，2012.

[4]温任林，颜景平.汽车发动机悬置系统多目标优化的研究[J].东南大学学报，1996，26（6A）：105-110.

[5]赵子衡，韩旭，姜潮.基于近似模型的非线性区间数优化方法及其应用[J].计算力学学报，2010，27（3）：451-456.

[6]SHAN SONG QING,WANG GARY.Metamodeling for high dimensional simulation-based design problems[J].Journal of Mechanical Design,2010,132(5).

[7]王登峰，李未，陈书明，等.动力总成振动对整车行驶平顺性的传递路径分析[J].吉林大学学报，2011，41(A2)：92-97.

[8]ISO 3471:2008 Earth-moving machinery—Roll-over protective structures—Laboratory tests and performance requirements[S].2008.

[9]孙海燕，丁咚.薄板样条函数及复杂曲面的数学表示[J].测绘工程，2006，15(2)：7-8.

[10]谢涛，陈火旺，康立山.多目标优化的演化算法[J].计算机学报，2003，26(8)：997-1003.

[11]刘伟.客车悬架橡胶衬套对整车性能影响研究与多目标优化[D].长春：吉林大学，2012.

NVH Performance Optimization of Bus Engine Mounting Systems Based on High Dimensional Model Representation

LI Wei-ping,YIN Wen-feng,ZENG Liang-ming,YANG Yu-qing,MAO Guang-jun
（State Key Laboratory ofAdvanced Design and Manufacture for Vehicle Bodyies,Hunan University,Changsha 410082,China）

Vehicle NVH performance is an important indicator to measure the vehicle’s ride comfort.The noise level and vibration amplitude of vehicles directly affect the passengers’subjective feelings.In this study,through NVH test of vehicles in idle condition,it is found that the engine mounting system has the greatest influence on the NVH performance at the driver’s seat.Then,the stiffness and damping at the four points of the powertrain suspension system are selected as the design variables,the high-dimensional model based on thin plate spline interpolation(TPS-HDMR)is built as an approximate model to align the design variables with the objective function.With the help of genetic algorithms,the sound pressure level at the driver’s right ear is optimized with the vibration amplitude in the driver’s seat as a constraint condition.The results show that the NVH performance of the vehicle is significantly improved and the feasibility of this method is verified.

vibration and wave;NVH test;mounting system;thin plate spline interpolation;approximate model;genetic algorithm

TB535

A

10.3969/j.issn.1006-1355.2017.06.012

1006-1355(2017)06-0061-06

2017-03-17

湖南省自然科学基金资助项目（2015JJ2029）

李伟平（1971-），男，湖南省邵阳市人，博士，副教授，主要研究方向为汽车NVH及优化、汽车动力学。

尹文锋，男，硕士研究生。E-mail:15111493676@163.com