可变外激励下制动器低频振动的实验与数值仿真

张佳慧

（上海理工大学 土木工程系，上海 200093）

可变外激励下制动器低频振动的实验与数值仿真

张佳慧

（上海理工大学 土木工程系，上海 200093）

在实验和数值仿真的基础上，利用三自由度模型来预测制动系统的动力响应，即可变外激励下的制动器低频振动。实验中制动器参数可调，外激励可变。采用事件驱动法对制动器低频振动进行数值仿真，实验和数值仿真中均可测得制动器低频振动，证明数值模拟结果可靠。通过实验与数值仿真观测制动系统参数变化以及外激励对其低频振动的影响，发现制动系统低频振动对其自身参数改变十分敏感；同时，选取适当形式的外激励可以抑制制动器的低频振动。

振动与波；制动系统；外激励；低频振动；三自由度模型

制动系统在制动过程中产生的低频自激振动和高频噪声会缩短刹车部件的使用寿命，降低运载工具的乘用舒适度，甚至引起整个系统的失稳。常用的制动器分为盘式制动器和鼓式制动器。根据其结构特性，学者提出了不同的动力学模型和理论，诸如与速度相关的摩擦系数理论[1–2]，stick-slip模型[3]，sprag-slip模型[4]以及模态耦合失稳模型[5]。相对于高频噪声，制动器制动时产生的低频振动对乘运系统的舒适度影响更大。文献[6]依据频率高低对制动器振动进行分类，其中制动器低频振动可以分为冷颤动和热颤动。文献[7]采用三自由度动力学模型来解释制动器低频振动。在该模型中采用了恒定外激励模式，而实际的制动器外激励的力值、频率均可变。因此，本文采用改进后的三自由度动力学模型进一步深入研究制动器的低频振动。

本文通过实验和数值仿真研究制动器的低频振动。在三自由度动力学模型基础上进行实验测试，通过实验装置实现制动器参数可调、外激励可变。第二步利用数值仿真模拟制动器低频振动，采用事件驱动法判别制动盘的接触与脱离。在实验和数值仿真的基础上，考察低频振动对制动器参数变化的敏感性，找出能够抑制制动器低频振动的较优外激励形式。

1 三自由度制动器动力学模型

摩擦引起的自激振动，通常被认为是制动器在制动时失稳的主要原因。文献[7]将此类低频振动归因于制动器制动部件和承运工具前桥的共同作用，因此在三自由度模型中考虑前桥对制动器低频振动的影响，见图1。在该模型中，两自由度x、y用来表征制动踏板的平面内运动，而另一自由度Y则用来描述前桥的竖向运动。需要注意的是，真实的制动力大小与频率均可变。本文在文献[7]基础上，将恒定制动力变为可变制动力，采用改进后的三自由度动力学模型研究制动器的低频振动。改进后三自由度模型详情见文献[8]。

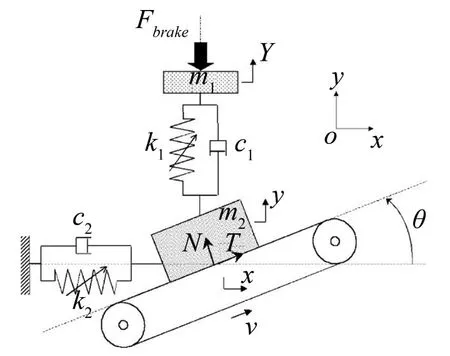
图1 制动器三自由度动力学模型

三自由度模型的运动方程如下

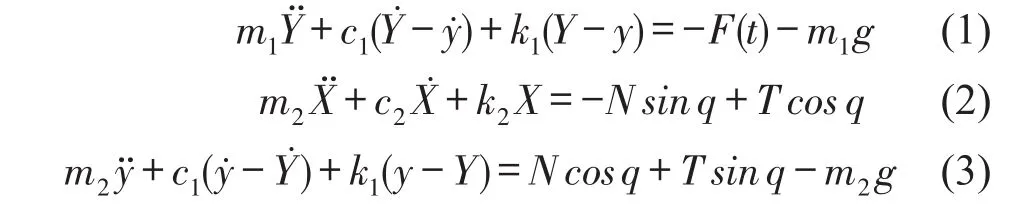
式中T和N分别代表切向摩擦力和法向支持力；X和y分别描述质块m2的运动，而Y描述质块m1的运动。在动力学模型中，假定摩擦系数为常值，因此采用库伦摩擦定律表征摩擦力T=μN。模型中的外激励（制动力）表征为F(t)。利用制动角θ得到y=Xtanθ,同时当质块m2与皮带保持接触状态时，三自由度模型可以简化为两自由度模型，如下式

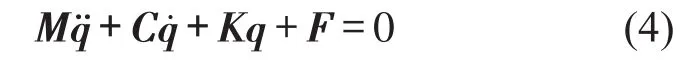
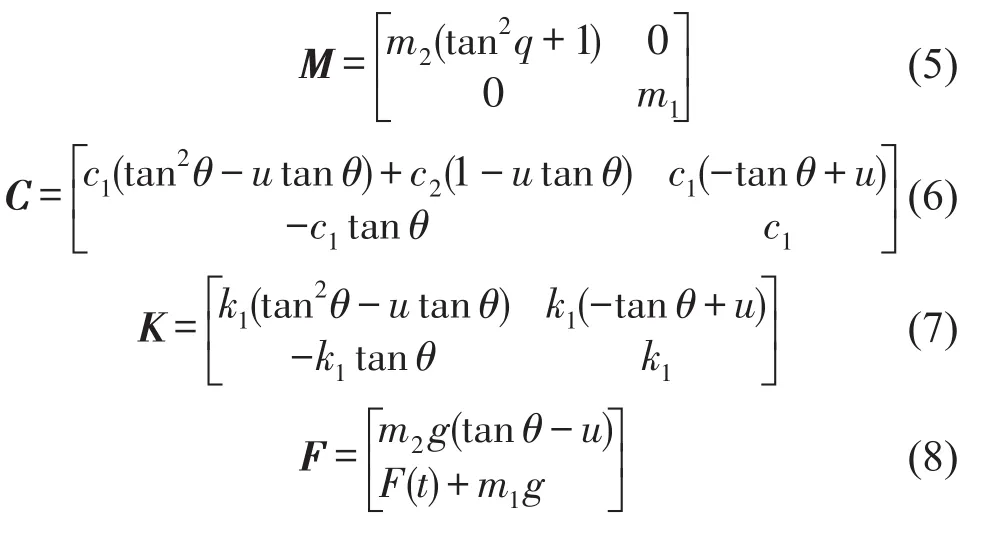
当质块m2与皮带脱离接触，则N=0，T=0且因此，在采用三自由度动力学模型表征制动行为时

2 实验测试

本文基于改进后的三自由度模型进行实验装置设计。为了实现外激励（制动力）以及制动器参数可变，实验装置在设计中满足下列要求：平动带速度与制动角可变，弹簧-阻尼系统可换，外激励力值大小、波形与频率均可调，如图2所示。

图2 实验装置图

激振器接受信号发生器的信号，产生外激励（制动力）作用在质块m1上。质块m1将制动力传递至质块m2并影响质块m2与平动皮带的接触状态。实验装置的参数如下：m1=1 kg，m2=2 kg，k1=9 224 N/m，k2=9 224 N/m，c1=21.6 N/m·s-1，c2=21.6 N/m·s-1，μ=0.32。实验装置具体设计方案与详图见文献[8]。

实验中，电动机驱动转子带动平动皮带，平动皮带与质块m2发生摩擦。为了观测、记录制动系统的动力响应，实验中分别在Y，y和X三个方向放置速度传感器，在质块m1上放置力传感器。为了实现外激励可变，首先由信号发生器发送特定波形和频率的信号，激振器再将该信号转换成制动力传送至质块m1。实验中所有速度传感器和力传感器信号通过信号放大器放大并被数据采集仪记录接收。

3 制动系统的数值仿真

3.1 概述

与实验相比，采用数值仿真进行参数分析成本低、效率高。本文使用商用软件Matlab对制动器低频振动进行数值仿真。在数值仿真过程中，需要对三自由度模型中质块m1和m2的运动状态进行判别，这是确保数值仿真结果可靠的关键因素。

3.2 制动系统运动状态的判别

制动踏板与制动盘的接触摩擦，对应于制动器模型中质块m2与平动带，是判别制动系统运动状态的关键。当质块m2与平动带保持接触状态，质块m2的运动状态即为“stick”或“slip”，其中“stick”表示质块m2与平动带之间不发生相对滑动，即为黏滞状态。而“slip”表示质块m2与平动带之间发生相对滑动，即运动状态从黏滞转换为滑动。当质块m2与平动带脱离，则称为脱离接触状态。需要注意的是，这三种运动状态之间的变换不是单向的，即此三种运动状态中的任意两者之间在满足一定条件下可以相互转换。运动状态的转换条件见图3。图中N为质块m2与平动带的法向接触力，gN与VT分别表示质块m2与平动带的间距和相对速度。

3.3 制动系统数值仿真结果的校验

图3 制动系统运动状态判别

为了验证数值仿真结果的可靠性，需要将数值仿真的结果与实验结果进行比较和对照。在对比中，需要使数值仿真中的制动系统参数与实验保持一致。系统参数分别设定为：平动带速度为2 m/s，外激励力值为10 N，频率为50 Hz，波形为正弦波。实验与数值仿真所得Y方向速度的功率谱密度见图4。

图中可见外激励主频率为50 Hz，同时可以在图中发现第二、第三主频分别为100 Hz和150 Hz。更重要的是，在实验和数值仿真图像中，均可发现在15 Hz～40 Hz之间存在低频振动。通过两者对比发现，可以采用事件驱动法对三自由度制动系统模型进行数值仿真。

4 制动系统的参数分析

本节采用数值仿真分析制动系统的低频振动对系统参数变化的敏感性；此外，通过实验和仿真考察外激励对低频振动的抑制作用，找出抑制制动器低频振动的较优外激励形式。

利用数值仿真对制动系统变参数进行敏感性分析，见图5、图6。质块m2的三种运动状态“stick”、“slip”和“free flight”分别用黄色实线，蓝色虚线和绿色实线标注。如图5所示，当制动系统的平动带速度从0.25 m/s轻微升至0.28 m/s后，质块m2在X方向上的运动状态发生了巨大的变化。表现为“stick”随着平动带速度的增加而消失，同时质块m2在X方向上的位移和速度均大幅降低。在数值仿真中,将竖向弹簧-阻尼系统的刚度从4 000 N/m增加至5 000 N/m后，对应的质块m1在Y方向上的运动状态也发生了相应的改变。质块m1在Y方向的运动速度随着竖向弹簧-阻尼系统的刚度增加而减小，同时其在竖向的位移绝对值也减少了近一半。与之对应，质块m2的运动也发生了变化，即在图上表现为“stick”现象消失。

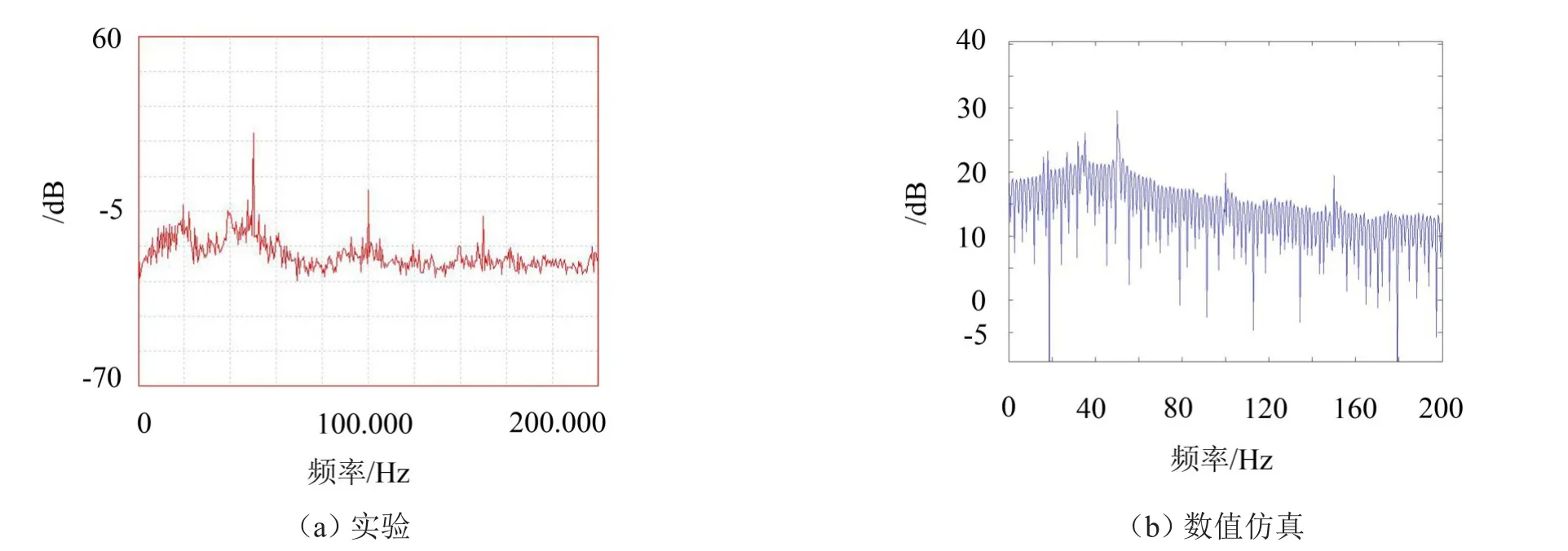
图4 Y方向速度功率谱密度

表1给出了具有相同频率（50 Hz）、不同波形的制动力作用下实验测得的制动系统Y方向噪声强度。表1中同时列出无外激励时Y方向噪声强度作为参考。通过对比可以发现，当施加外激励后，Y方向第一主频率噪声强度由18.68 dB下降至4.05 dB、-1.02 dB、-9.18 dB。其中白噪声的抑制效果最为显著。在Y方向第二、第三主频率上可以发现类似的趋势。

实验测得在不同外激励形式下制动系统的动力响应见表2、表3。与预期相悖，对制动系统的低频振动施加外激励并不总能取得良好效果。如表2所示，20 Hz的三角波和方波形式的外激励没有降低制动系统的动力响应，特别是在Y方向的加速度峰值和均方根均有不同程度的增加，表明乘运工具的舒适度下降。当外激励三角波和方波的频率增加至50 Hz或100 Hz后，与不施加外激励工况对比，能够显著降低制动系统X方向的动力响应，但在Y方向上抑制低频振动的效果仍不明显。因此，此组实验表明，三角波和方波可能不是抑制制动系统低频振动的理想外激励波形。

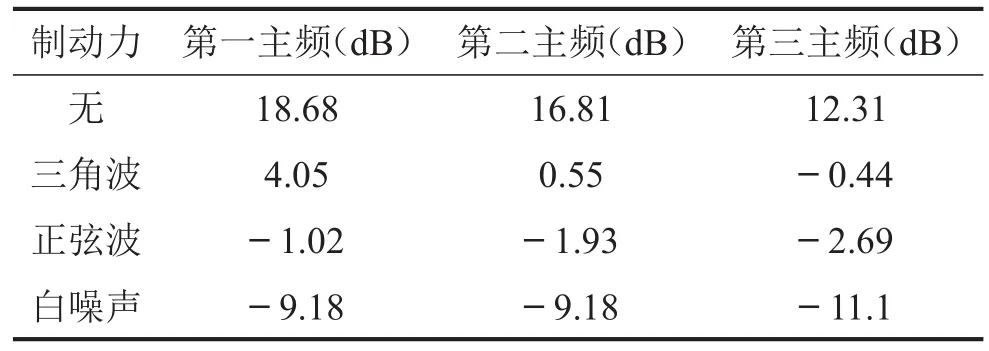
表1 制动系统Y方向噪声强度

表2 制动系统X、Y方向的动力响应

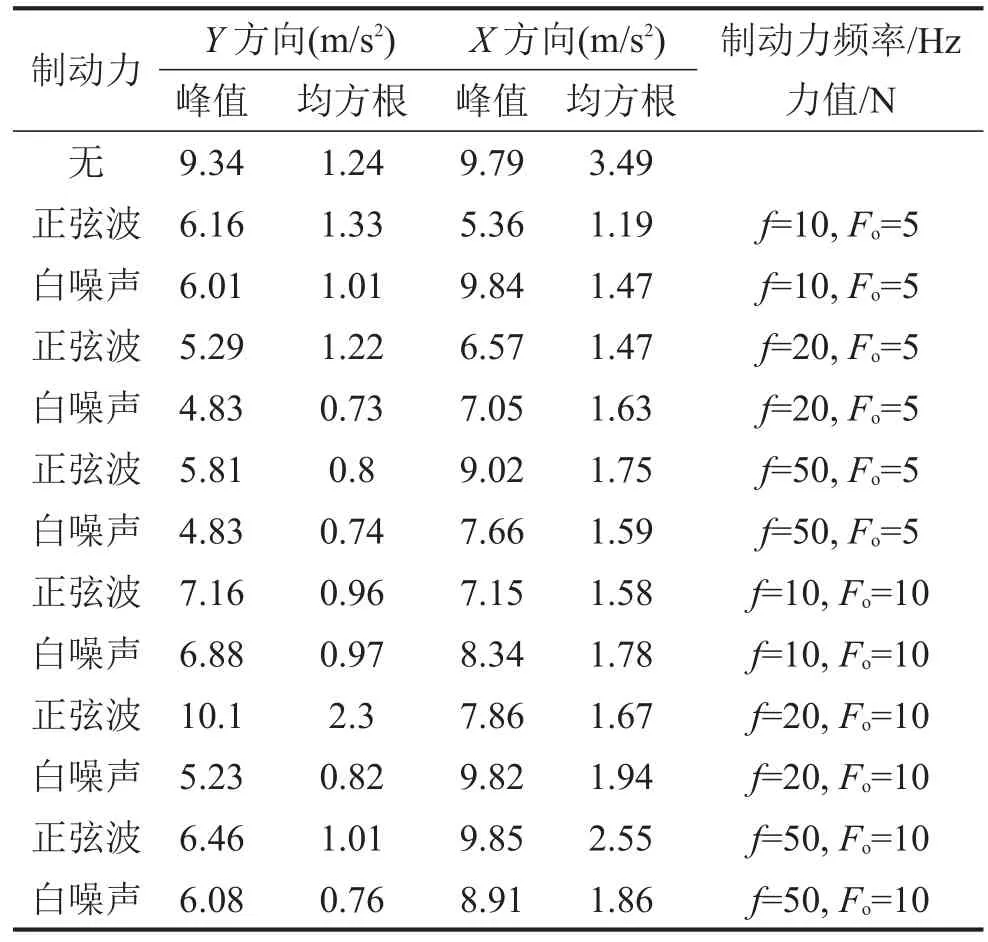
表3 制动系统X、Y方向的动力响应

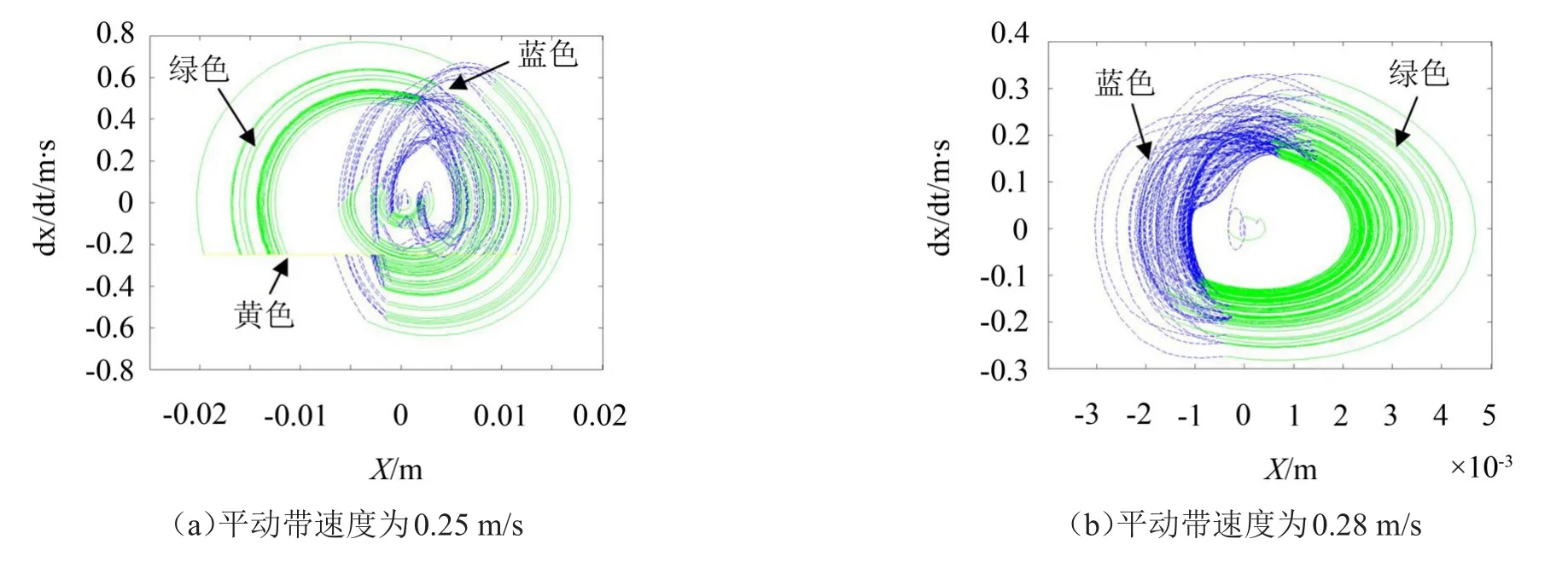
图5 数值仿真中X方向相平面图（速度-位移）

表3给出了正弦波和白噪声抑制低频振动的实验数据。实验数据表明白噪声抑制低频振动的效果优于正弦波。需要注意的是，正弦波在特定频率和力值组合下可以表现出较好的抑制效果，例如50 Hz与5 N、10 Hz与10 N，但在另一些力值与频率的组合中无法发挥抑制低频振动的作用，例如20 Hz与10 N。

根据数值仿真的结果也可发现，正弦波和白噪声是抑制制动系统低频振动的较优波形。图7给出了在正弦波和白噪声激励下的制动系统Y方向速度-位移庞加莱图。

图中红色实线、蓝色虚线和绿色实线对应于制动系统中质块m2的三种运动状态即黏滞、滑动和脱离接触。正弦波激励下，图中出现了环状结构和吸引子，这表明制动系统发生概周期运动。当对制动系统施加白噪声形式外激励后，如图所示，制动系统表现出了一定程度的混沌现象。由于白噪声频带较宽，因此每一振动频段所对应的振动能量较低。这可以用来解释白噪声能较好地抑制制动系统低频噪声的原因。

5 结语

在实验和数值仿真的基础上，利用三自由度系统来预测制动系统的动力响应。通过实验和数值仿真分别实现可变外激励和制动参数可调。在数值仿真中采用事件驱动法判别制动系统运动状态的转换。与实验数据的对照证明数值仿真结果可靠。通过实验结果和数值仿真数据发现，制动系统的动力响应对其参数改变十分敏感。同时，实验和数值仿真的结果表明，白噪声是比较理想的抑制制动系统低频振动的外激励源。

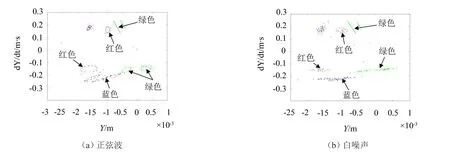
图7 数值仿真中Y方向庞加莱图

[1]H R MILLS.Brake squeal[R].Technical report N900B,Institution ofAutomobile Engineers,1938.

[2]R A C FOSBERRY,Z HOLUBECKI.An investigation of the cause and nature of brake squeal[R]Motor Industry ResearchAssociation,1955.

[3]F HESLOT,T BAUMBERGER,B PERRIN,et al.Creep,stick-slip,and dry-friction dynamics:Experiments and a heuristic model[J]Physical Review E.,1994,49(6):49-73.

[4]SINOU J J,THOUVEREZ F,JEZEQUEL L.Analysis of friction and instability by the centre manifold theory for a non-linear sprag-slip model[J].Journal of Sound andVibration,2003,265(3):527-559.

[5]CHUNG CH J,DONLEYM.ModeCoupling Phenomenon of Brake Squeal Dynamics[C]//SAE 2003 Noise&Vibration Conference and Exhibition,2003.

[6]J D ANDREW.Braking of road vehicles[R].Butterworth-Heinemann Ltd,2014.

[7]J J SINOU,F THOUVEREZ,L JEZEQUEL.Analysis of friction and instability by the centre manifold theory for a non-linear sprag-slip model[J]Journal of Sound and Vibration,2003,265(3):527-559.

[8]张佳慧，冯奇.Sprag-slip现象实验设计及初探[J].噪声与振动控制，2008，28(6)：92-96.

Experimental and Numerical Study on Low-frequency Vibration of Brakes with Variable External Excitation

ZHANG Jia-hui
（Department of Civil Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

The low-frequency vibration of brakes under variable external excitation is studied experimentally and numerically.In the experiment,the mechanical parameters are changeable and the external excitation is variable,which is realized by using an external exciter with a waveform generator.The low-frequency data of the brake system is obtained.Then,a 3-DOF model is established to predict the dynamic behavior of the brake system.The numerical simulation is carried out using the event-driven method.The results of low-frequency vibration are compared with those of the experiment and the correctness and reliability of the numerical simulation are verified.The influence of the mechanical parameters and the external excitation on the low-frequency vibration is analyzed.It is shown that the low-frequency vibration of the brake system is sensitive to the variation of the mechanical parameters,and the pertinent selection of the external excitation can effectively suppress the low-frequency vibration of the brake system.

vibration and wave;brake system;external excitation;low-frequency vibration;3-DOF model

O422.6

A

10.3969/j.issn.1006-1355.2017.06.009

1006-1355(2017)06-0046-05

2017-09-21

张佳慧（1981-），男，浙江省鄞县人，硕士生导师，主要研究方向为动力学与控制。E-mail:zhangjh316@163.com