舰载飞机着舰时拦阻钩碰撞反弹动力学分析

彭一明，聂宏

南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016

舰载飞机着舰时拦阻钩碰撞反弹动力学分析

彭一明，聂宏*

南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016

为了解舰载飞机着舰时拦阻钩碰撞甲板后被反弹的动力学性能，以某舰载飞机为研究对象，建立了全机着舰动力学模型和拦阻钩碰撞甲板的碰撞模型，进行了全机着舰动力学仿真，通过拦阻钩碰撞反弹试验对碰撞模型进行修正，得到了更加准确的碰撞模型。将仿真结果与试验结果进行对比，验证了模型的准确性。研究了甲板涂层、俯仰角、航向速度、下沉速度和拦阻钩阻尼器参数对拦阻钩反弹动力学性能的影响。结果表明：航向速度对反弹高度和碰撞力几乎没有影响；随着下沉速度和俯仰角的增加，反弹高度和碰撞力也增加；拦阻钩阻尼器参数的变化不会影响碰撞力，但是对反弹动力学性能会产生明显的影响。

舰载飞机；拦阻钩；碰撞；动力学；阻尼器

拦阻钩是舰载飞机较陆基飞机的一个显著区别，其主要作用是在飞机顺利进场后钩住航母拦阻索，将拦阻力传递到机身上，强制飞机减速。通常，舰载飞机着舰时拦阻钩最先与甲板碰撞，并在拦阻钩纵向阻尼器作用下发生有限高度的弹跳，同时，在飞机牵连运动下，钩头与稍高出甲板表面悬空横置的拦阻索啮合。

拦阻钩与甲板碰撞后拦阻钩以一定的反弹角速度反弹，如拦阻钩反弹的高度过高，则会导致挂索失败。为使拦阻钩能够成功拦套住其中一根拦阻索，第1次反弹必须保证不超过长6.1 m和高100 mm[1-2]。如何抑制拦阻钩反弹成为保证拦阻成功的首要条件，因此对拦阻钩碰撞动力学进行深入研究尤为重要。

国外对拦阻钩碰撞动力学的研究已经很成熟，但由于保密的原因，能查到的相关文献极其有限，这些有限的文献也只有一些理想状况下的理论结果。例如，Thomlinson[3]对飞机对称面内拦阻钩撞击甲板后的运动情况作过详细研究，假设舰载飞机无偏航对中拦阻，通过分析飞机、道面和拦阻钩组成的三角关系，建立运动微分方程。全美工程公司公布的一份报告[4]对拦阻钩碰撞悬索支撑物的情况进行了分析。

近年来，国内学者对飞机拦阻钩碰撞动力学进行了大量理论研究，研究内容都是拦阻钩碰撞甲板[5-8]。在这些研究中，均是在Thomlinson的研究基础上引入碰撞理论进行理论计算，模型假设比较理想，无法反映飞机着舰时的实际情况。国内学者针对拦阻钩碰撞问题还进行了一些试验研究，杨全伟[9]对舰载飞机拦阻着舰时拦阻钩的载荷进行了实测，但其研究内容偏重于载荷，并未对反弹高度、反弹距离等动力学性能进行分析；从一些未公开的资料中得知，国内有学者对拦阻钩反弹问题进行了试验研究，试验中使用钢板来模拟甲板，且模拟了着舰时的下沉速度，获得了一些很有价值的试验数据，但该试验并未考虑航向速度以及甲板表面涂层对拦阻钩弹跳性能的影响，试验结果存在一定的误差。

通常，虚拟样机较理论模型更加接近实际情况，而在研究拦阻钩碰撞问题时，很少有人使用虚拟样机技术，主要原因在于虚拟样机建模比较复杂、碰撞参数难以确定且模型难以验证。本文使用虚拟样机技术建立了某型舰载飞机全机着舰模型，采用Hertz接触模型定义拦阻钩与甲板的碰撞力，通过拦阻钩碰撞反弹试验对碰撞模型的参数进行修正，验证了模型的准确性，分析了不同参数对拦阻钩碰撞反弹运动过程的影响。

1 全机着舰动力学建模

1.1 多刚体动力学模型

全机着舰动力学模型主要基于多体动力学理论，应用拉格朗日待定乘子法，多刚体系统的动力学方程[10]可表示为

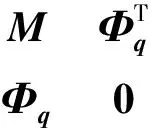
(1)

每个刚体的运动用7个广义坐标描述，[x，y，z，e0，e1，e2，e3]。其中欧拉四元数[e0，e1，e2，e3]用于描述刚体在空间的姿态，这有效解决了采用欧拉角或科比角可能产生的矩阵奇异问题[11]。由于采用了不独立的广义坐标，系统动力学方程是高度稀疏的微分代数方程，适于用稀疏矩阵的方法进行高效求解。

1.2 缓冲器力模型

本文中飞机起落架缓冲器为单腔-变油孔-油气式。缓冲器的支柱作用力Fs包括空气弹簧力Fa、油液阻尼力Fh和结构限制力Fl,即

Fs=Fa+Fh+Fl

(2)

不考虑油液的可压性和缓冲器腔体的体积变化时，空气弹簧力为[12]

(3)

式中：Aa为压气面积；P0为缓冲器初始填充压强；V0为缓冲器初始充气容积；n为气体多变指数；Patm为当地大气压强；s为缓冲器行程。

缓冲器主油腔油孔为变油孔，且有侧油孔，则油液阻尼力为[12]

(4)

式中：ρoil为油液密度；Ah为缓冲器有效压油面积；Ad为主油腔油孔面积；Cd为主油腔油孔缩流系数；Ahs为缓冲器回油腔有效压油面积；An为回油腔油孔面积；Cds为回油腔油孔缩流系数。

缓冲器结构限制力Fl可表示为

(5)

式中：kl为结构限制力刚度系数；smax为缓冲器最大行程。

本文中拦阻钩的阻尼器为单腔-常油孔-油气式，没有侧油孔，在计算阻尼器作用力时只需将油液阻尼力的公式换成式(6)即可，其他公式与起落架缓冲器作用力一致。

(6)

式中：AZh为拦阻钩阻尼器有效压油面积；AZd为阻尼器油孔面积。

1.3 轮胎力模型

轮胎力学特性是影响飞机起落架着陆(或着舰)性能的重要因素，建立较为准确的轮胎力模型对整个起落架的精确建模至关重要。

本文使用的轮胎力模型是基于点接触理论[13]建立的,该轮胎模型可以对轮胎的动态性能、路面形状与胎面的接触等进行描述。该模型除点接触理论以外的各方向力的计算方法如下所述。

如图1所示，在轮盘平面内，将轮胎分成若干窄条形单元。每个受压单元分别计算压缩面积Ai。以Ai为权系数，计算各单元受压部分的质心坐标Cpi的加权平均值及受力方向gi的加权和的方向，作为轮胎垂向力的作用点Cp和方向g,即[14]

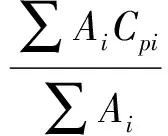
(7)

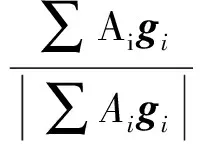
(8)

轮胎侧向力是关于轮胎垂向力与轮胎侧偏角的函数。如图2所示，轮胎侧向力与轮胎侧偏角的立方成正比，并满足式(9)描述的边界条件。

(9)

式中：α为轮胎侧偏角；αn为饱和侧偏角；Cα为轮胎侧偏刚度；Flat为轮胎侧向力；(Flat)max为轮胎饱和侧向力，等于滑动摩擦系数μ与轮胎垂向力Fnorm的乘积[14]。

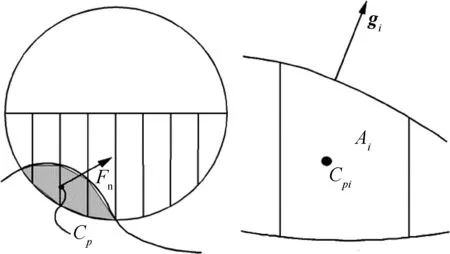
图1 轮胎垂向力计算方法示意图[14]Fig.1 Schematic diagram of tire normal force calculation method[14]

图2 轮胎侧向力计算方法示意图[14]Fig.2 Schematic diagram of tire lateral force calculation method[14]

1.4 碰撞力模型

在着舰过程中，拦阻钩钩头会与甲板以极短的时间相接触发生碰撞反弹，这种碰撞中的接触力可用Hertz接触模型来模拟。Hertz接触模型需满足3个假设[15]：接触区发生小变形；接触面呈椭圆形；相接触的物体可被看做是弹性半空间。

在此进行合理的假设：

1) 钩头与甲板碰撞的时间极短，文献[1]中认为碰撞时间为10-4～10-3s。在如此短的时间内，可以认为接触系统的两个物体之间不发生刚体运动。

2) 钩头与甲板的刚度都很大，碰撞时它们的变形是小变形。

3) 钩头碰撞部位为圆滑的曲面，因此可以近似认为接触面为椭圆形。

本文所研究的接触系统并非规则的球与平板的接触，所以选择Hertz接触理论中的通用公式[16](该公式适用于除了平行圆柱外的任何规则形状物体的接触问题)来定义钩头与甲板之间的碰撞力F。

(10)

式中：δ为两个接触体的合成变形。

(11)

(12)

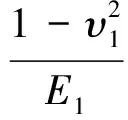
(13)

cosθ=

(14)

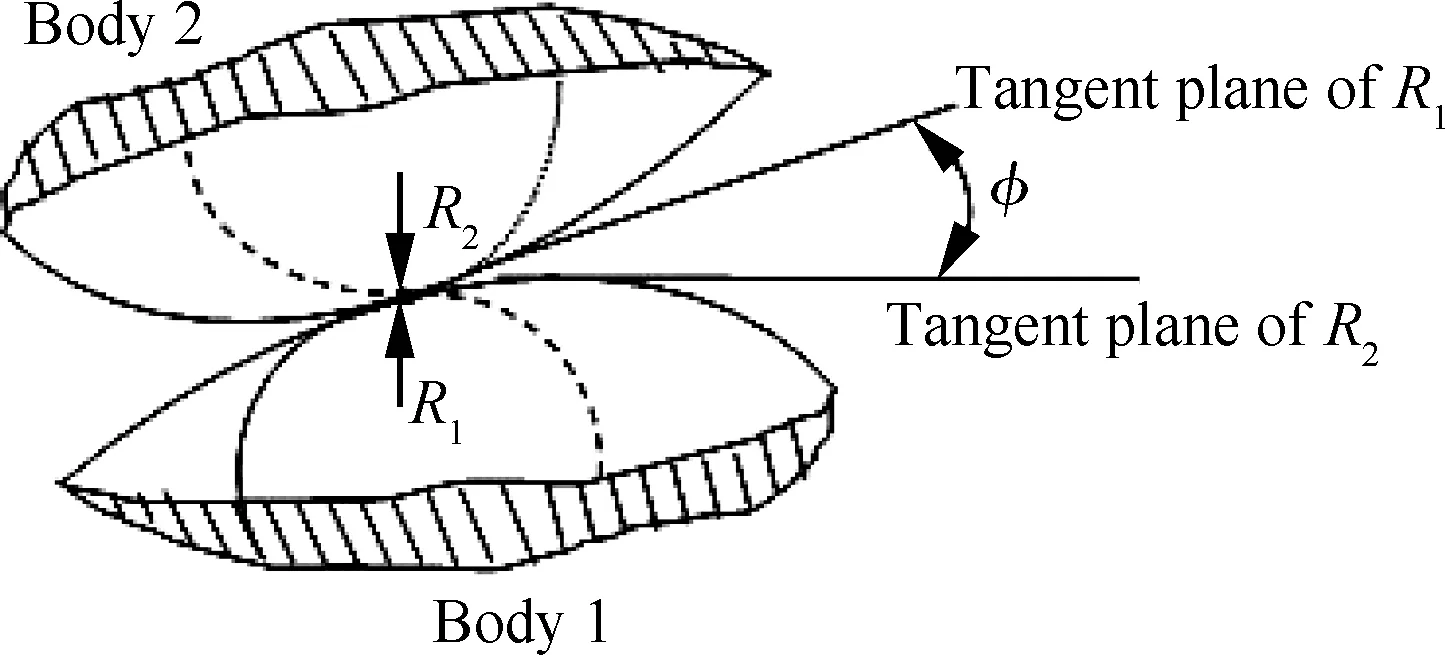
图3 Hertz接触力模型Fig.3 Hertz contact force model

计算出cosθ之后，可以根据文献[15]中给出的表格直接查询得到λ,在模型计算时则需要将cosθ和λ之间的关系拟合成函数关系，即

(15)

2 拦阻钩碰撞反弹试验

恢复系数的选取直接影响碰撞反弹高度，决定了模型的准确性以及结果的可信度。牛顿在研究正碰撞的规律时发现，对于材料确定的物体，碰撞结束与碰撞开始的速度大小的比值e几乎是不变的，称之为恢复系数[17-18]。在经典的理论力学[17]中钢球与钢球的碰撞恢复系数为5/9，在文献[19]中，某柔性梁与刚性地面之间的碰撞恢复系数为0.6，而甲板上有一层粗糙的涂层，钩头与其碰撞情况比较复杂，恢复系数难以确定。

由于国内外尚未公开关于拦阻钩弹跳方面的试验资料，为确定仿真模型的参数，如恢复系数、弹性模量、摩擦系数等，校核仿真模型的准确性，需进行拦阻钩碰撞反弹试验研究。通过拦阻钩碰撞反弹试验，主要修正恢复系数和弹性模量两个关键参数，前者直接影响拦阻钩的弹跳高度，后者为碰撞力的主要影响因素。

拦阻钩碰撞反弹试验方案如图4所示，将拦阻钩安装在吊篮侧面，通过定高度投放吊篮来模拟拦阻钩碰撞时的下沉速度；拦阻钩钩头下方是一个高速旋转的圆盘，钩头与圆盘的碰撞点位于圆盘的边缘，圆盘沿飞机逆航向转动，碰撞点处钩头与圆盘相对线速度与飞机着舰时的航向速度一致；为了更加准确地模拟碰撞工况，在圆盘上涂上甲板涂层，使碰撞点的材料属性、力学性能均与甲板上的相同。

图4 拦阻钩碰撞反弹试验示意图Fig.4 Schematic diagram of test of arresting hook bounce

试验中，下沉速度VV的计算公式为

(16)

式中：h为投放高度；Md为吊篮及拦阻钩的质量；gd为重力加速度；f为吊篮自由落体时受到的摩擦力。

航向速度VE的计算公式为

VE=2πNR

(17)

式中：N为圆盘的转速；R为钩头与圆盘碰撞点的旋转半径。

3 模型校验

利用第1节建立的全机着舰仿真模型进行仿真计算，仿真计算结果与第2节的试验结果进行对比，对模型中的关键参数进行修正，从而得到更加精确的模型用于最终的仿真分析。飞机的主要仿真参数如下：

着舰重量WL=2×105N,俯仰角θP=0°,滚转角θR=0°,偏航角θY=0°,拦阻钩甲板角β=58°,泊松比υ1=υ2=0.3,拦阻钩钩头弹性模量E1=210 GPa ,甲板弹性模量E2=210 GPa ,恢复系数e=0.6。

拦阻钩碰撞反弹试验可供对比的工况如表1所示，表中PZ0为拦阻钩阻尼器的充气压力。可供对比的结果为初次碰撞的接触力和初次碰撞后反弹的高度。

基于试验结果中的碰撞接触力以及反弹高度，对仿真模型中的恢复系数、甲板弹性模量进行修正，最终确定恢复系数取0.43，甲板由于有涂层的存在，其弹性模量取30 GPa。

使用修正后的参数重新进行仿真计算，仿真计算的结果与拦阻钩碰撞反弹试验结果的对比如表2所示。

通过仿真结果与试验结果的对比，除了工况2 中接触力的误差为9.67%，其余结果的误差均小于5%，表明本文所建立的拦阻钩碰撞反弹动力学模型较为精确，可用于拦阻钩碰撞反弹动力学仿真分析。

表1 仿真和试验的对比工况Table 1 Parameters of simulation and test

表2 仿真结果与试验结果的对比Table 2 Comparison of simulation and test results

4 计算与分析

主要仿真参数初始取值为：WL=2×105N,θP=0°,θR=0°,θY=0°,β=58°,e=0.43,E1=210 GPa ，E2=30 GPa ，υ1=υ2=0.3,VE=55 m/s,VV=6.3 m/s,PZ0=2 MPa,AZd=50 mm2。

4.1 甲板涂层对拦阻钩碰撞反弹的影响

为了分析甲板涂层对拦阻钩弹跳反弹性能的影响，对不考虑甲板涂层的模型进行仿真，甲板的弹性模量取E2=210 GPa ，恢复系数取e=0.6,得到的拦阻钩弹跳结果与第3节修正后考虑甲板涂层的模型的仿真结果进行对比，如图5所示。碰撞力F和拦阻钩阻尼器初次反弹过程中最大作用力FZs的对比结果如表3所示。

由图5可看出，甲板没有涂层时，拦阻钩与甲板碰撞后初次反弹的高度和距离明显增加，初次反弹高度为93 mm，反弹距离为4.5 m；而有甲板涂层时反弹高度为53 mm，反弹距离为3.5 m。从表3可以看出没有甲板涂层时碰撞力明显增大，碰撞力高达622 kN，阻尼器作用力略有增大，达到52.7 kN。

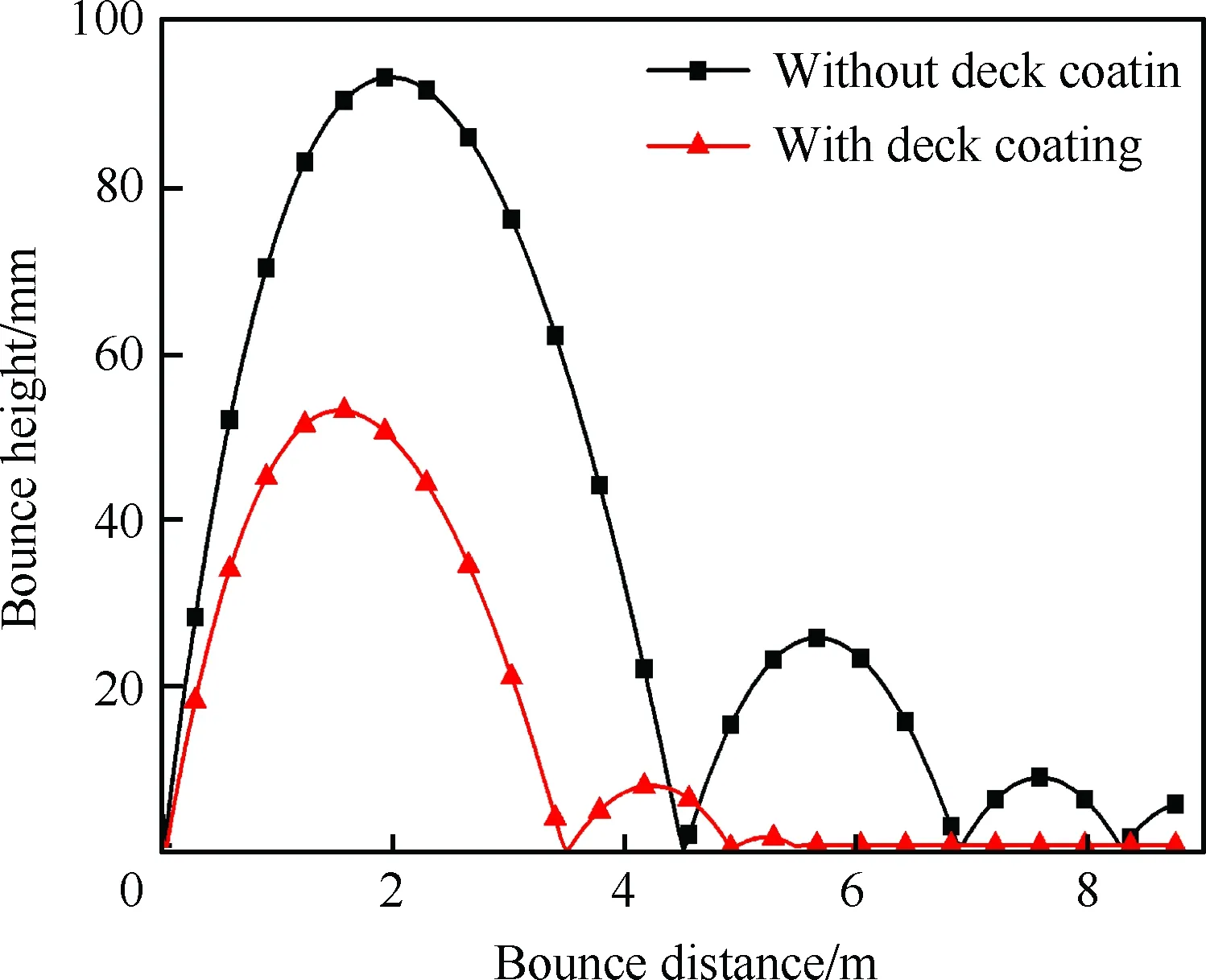
图5 有/无甲板涂层时拦阻钩钩头反弹高度变化Fig.5 Changes of bounce height of arresting hook after impacting with/without deck coating

表3 有/无甲板涂层时碰撞力和拦阻钩阻尼器作用力Table 3 F and FZs with/without deck coating

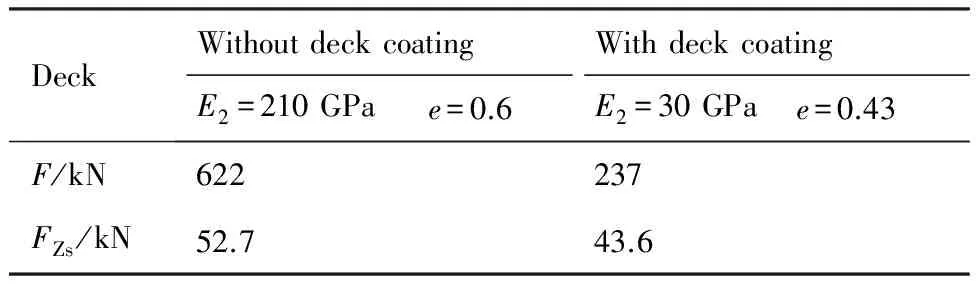
DeckWithoutdeckcoatingWithdeckcoatingE2=210GPae=0．6E2=30GPae=0．43F/kN622237FZs/kN52．743．6

4.2 下沉速度对拦阻钩碰撞反弹的影响

根据GJB 67.4A—2008中规定的内容，舰载飞机平均下沉速度不应小于3.505 2 m/s[20]，通过着舰速度可计算得到最大下沉速度为6.3 m/s，这与拦阻钩碰撞反弹试验中使用的两个下沉速度(3.6和6.3 m/s)相吻合。仿真计算时，分别选取飞机着舰下沉速度为3.6、4、5和6.3 m/s。由第3节修正后的模型进行仿真计算，得到不同下沉速度下拦阻钩碰撞后钩头的反弹高度，如图6所示。

将不同下沉速度下碰撞力F和拦阻钩阻尼器初次反弹过程中最大作用力FZs的结果列入表4 进行比较分析。

由图6可以看出，舰载飞机着舰时，随着下沉速度的增加，拦阻钩与甲板碰撞后初次反弹的高度也相应地增加，下沉速度为6.3 m/s时初次反弹高度为53 mm；初次反弹的距离随着下沉速度的增加略有增加，均未超过4 m。

从表4可看出碰撞力和阻尼器的作用力也随下沉速度的增加而增大。下沉速度为6.3 m/s时，碰撞力可达到237 kN，阻尼器作用力可达到43.6 kN。

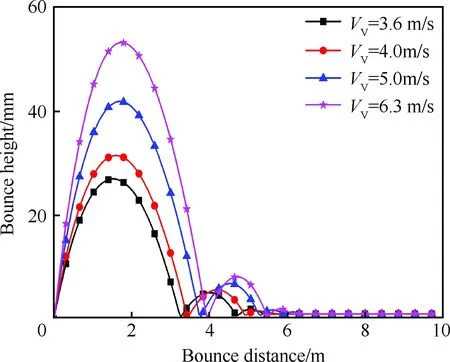
图6 不同下沉速度下拦阻钩钩头反弹高度的变化Fig.6 Changes of bounce height of arresting hook after impacting with different VV

表4 不同下沉速度下碰撞力和拦阻钩阻尼器作用力Table 4 F and FZs with different VV

VV/(m·s-1)3．64．05．06．3F/kN118122147237FZs/kN19．422．130．243．6

4.3 俯仰角对拦阻钩碰撞反弹的影响

取飞机着舰时的最大俯仰角为8°，分析俯仰角由0°变化到8°时拦阻钩碰撞反弹性能的变化趋势，其他参数取初始值,结果如图7所示。

将不同俯仰角下碰撞力F和拦阻钩阻尼器初次反弹过程中最大作用力FZs的结果列入表5进行比较分析。

飞机着舰时俯仰角的变化，对于拦阻钩碰撞来说主要改变了拦阻钩的甲板角以及钩头碰撞点，随着俯仰角的增大，拦阻钩甲板角相应增大。从图7中可看出，拦阻钩与甲板碰撞后初次反弹的高度随着俯仰角的增大而增大，这与文献[1,4,11]中随着甲板角的增大拦阻钩反弹角速度增大的结论相一致。当俯仰角为8°时，初次弹跳高度为81 mm，弹跳距离为4.57 m。

从表5中可以看出，随着俯仰角的增大，阻尼器的作用力明显增大，而碰撞力的变化规律并不明显，总体来说呈少量增大趋势。

由此可知，俯仰角增大时，影响拦阻钩反弹性能的主要是甲板角的变化，钩头碰撞点的变化对拦阻钩弹跳的影响很小。

图7 不同俯仰角下拦阻钩钩头反弹高度的变化Fig.7 Changes of bounce height of arresting hook after impacting with different θP

表5 不同俯仰角下碰撞力和拦阻钩阻尼器作用力Table 5 F and FZs with different θP

θP/(°)02468F/kN237220258278293FZs/kN43．650053．760．969．3

4.4 航向速度对拦阻钩碰撞反弹的影响

本文中选取了不同的航向速度进行仿真分析，分别为55、50、45、40和0 m/s，其他参数取初始值。

从图8中可以看出，随着航向速度的减小，拦阻钩与甲板碰撞后初次反弹高度几乎不变，仅有反弹距离随着航向速度的减小而减小。图8中4种情况对应的碰撞力和阻尼器作用力也相同，分别为238和43.6 kN。

值得关注的是，当航向速度设为0 m/s进行仿真时，钩头和甲板由于碰撞力太大出现了穿透现象，仿真结果显示碰撞力为1 100 kN。在第2节所述拦阻钩碰撞反弹试验中，如果圆盘不带转进行碰撞反弹试验，拦阻钩只会出现小量的反弹，严重时甚至会“别”住不发生反弹，且碰撞力会增大很多。这是由于甲板涂层摩擦系数很大，相应的摩擦力也很大，当圆盘不带转时，拦阻钩钩头受到的摩擦力阻碍其反弹；而当圆盘高速转动(模拟飞机着舰时的航向速度)时，拦阻钩钩头受到的摩擦力促使其反弹。因此，在进行拦阻钩碰撞反弹试验时，要尽量模拟出拦阻钩和甲板之间的航向速度，这样不仅可以准确获取碰撞力和反弹性能，也能避免拦阻钩因受载过大而被破坏。

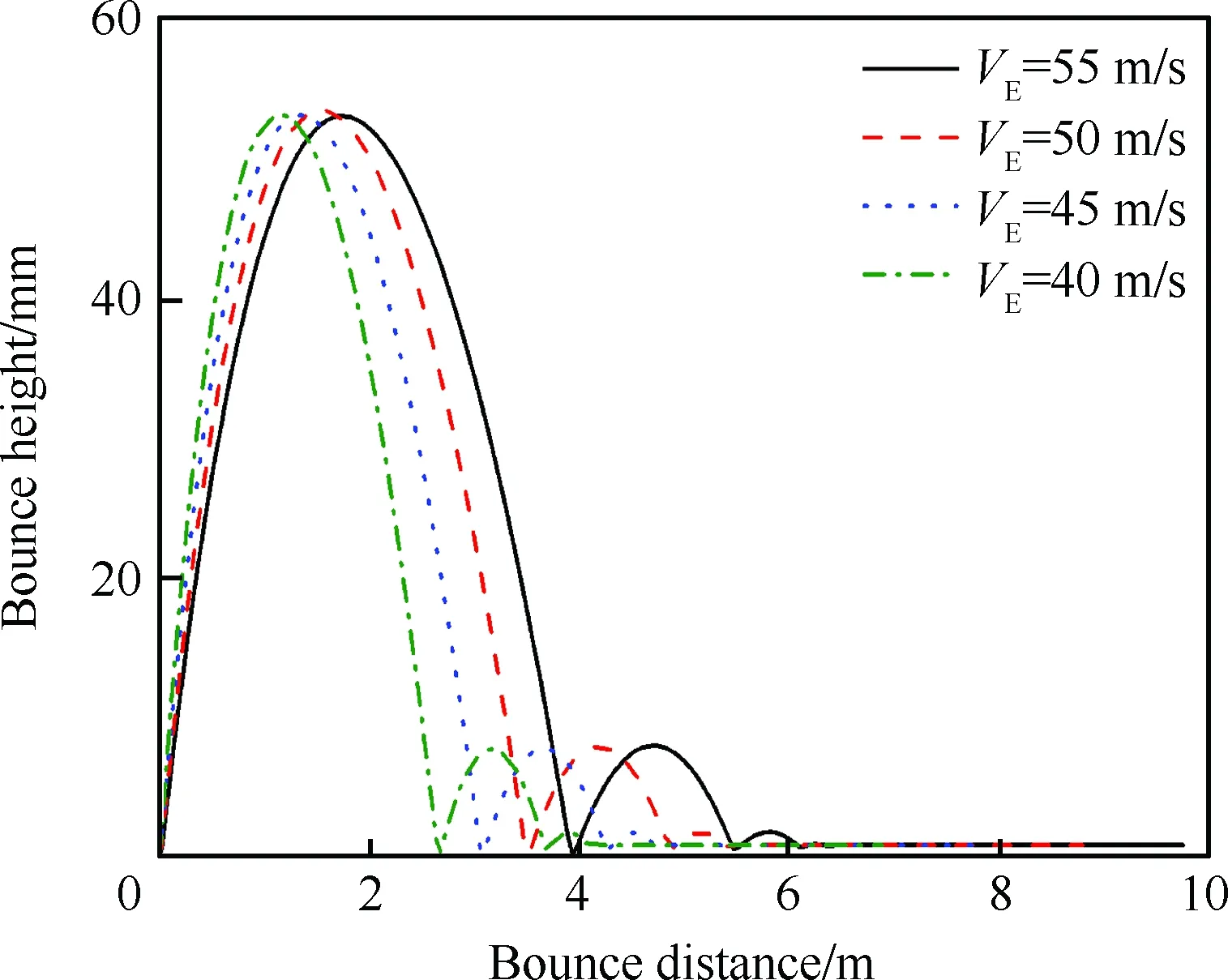
图8 不同航向速度下拦阻钩钩头反弹高度的变化Fig.8 Changes of bounce height of arresting hook after impacting with different VE

4.5 阻尼器参数对拦阻钩碰撞反弹的影响

文献[5]中由于不知道拦阻钩纵向阻尼器的内部结构和具体参数，认为纵向阻尼器是一个弹簧阻尼系统，通过选取合适的刚度系数和阻尼系数进行计算分析。本文在已知阻尼器是单腔-常油孔-油气式的基础上，通过变化阻尼器的充气压力PZ0来改变刚度系数，变化阻尼器油孔面积AZd来改变阻尼系数。

改变充气压力时，其他参数取初始值，拦阻钩初次反弹高度如图9所示。将不同充气压力下碰撞力F和拦阻钩阻尼器初次弹跳过程中最大作用力FZs的结果列入表6进行比较分析。

改变油孔面积时，其他参数也取初始值，拦阻钩初次反弹高度如图10所示。

同样，将不同油孔面积下碰撞力F和拦阻钩阻尼器初次反弹过程中最大作用力FZs的结果列入表7进行比较分析。

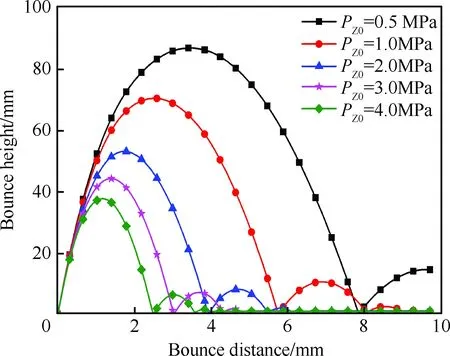
图9 不同充气压力下拦阻钩钩头反弹高度的变化Fig.9 Changes of bounce height of arresting hook after impacting with different PZ0

表6 不同充气压力下碰撞力和拦阻钩阻尼器作用力Table 6 F and FZs with different PZ0

图10 不同油孔面积下拦阻钩钩头反弹高度的变化 Fig.10 Changes of bounce height of arresting hook after impacting with different AZd

表7 不同油孔面积下碰撞力和拦阻钩阻尼器作用力Table 7 Results of F and FZs with different AZd

AZd/mm23040506070F/kN238238237238238FZs/kN10663．943．632．926．2

综合图9和图10可以看出，拦阻钩与甲板碰撞后初次反弹的高度随阻尼器充气压力的减小而增大，随阻尼器油孔面积的增大而增大。当充气压力为0.5 MPa(油孔面积为50 mm2)时，反弹高度为87 mm，弹跳距离为7.9 m，超过6.1 m，会导致挂索失败；当油孔面积为70 mm2(充气压力为2 MPa)时，反弹高度为108.2 mm，超过100 mm，同样会导致挂索失败。

充气压力和油孔面积的不同，对碰撞力几乎没有影响，但阻尼器作用力会随充气压力的增大而增大，随油孔面积的减小而增大。当油孔面积为30 mm2(充气压力为2 MPa)时，阻尼器最大作用力高达106 kN。

综上所述，需要合理选取阻尼器的参数，阻尼器作用力太小会导致拦阻钩反弹过高或过远，阻尼器作用力太大对其自身结构可能产生不利的影响。

4.6 各影响参数的最佳组合

本文分析了甲板涂层、下沉速度、航向速度、俯仰角、阻尼器参数对拦阻钩碰撞反弹动力学性能的影响，目标是为了减小拦阻钩的反弹高度、反弹距离、碰撞力以及阻尼器作用力。甲板涂层既能减小反弹高度和距离，又能减小碰撞力和阻尼器作用力，是必不可少的；下沉速度和俯仰角在给定的边界条件下越小越好；航向速度主要影响反弹距离，不宜太大；缓冲器参数的确定需权衡反弹高度与阻尼器作用力之间的矛盾关系，在下沉速度较小的情况下，可以选择大的充气压力和小的油孔，在下沉速度较大(如超过6 m/s)的情况下，需进行多次迭代确定最佳的参数组合。

本文选取以下的参数组合进行仿真计算：θP=0°,VV=3.6 m/s,e=0.43,E2=30 GPa,VE=55 m/s,PZ0=4 MPa,AZd=30 mm2。仿真结果如图11～图13所示。

由仿真结果可知，初次反弹的高度为8 mm，反弹距离为1.7 m，碰撞力峰值为119 kN，阻尼器作用力峰值为47.8 kN，拦阻钩反弹现象得到了很好的抑制，碰撞力偏小，阻尼器作用力在可接受范围内，本文认为这是一个比较合适的参数组合。

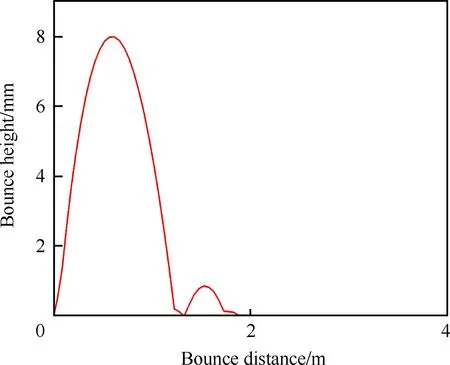
图11 拦阻钩钩头反弹高度的变化Fig.11 Changes of bounce height of arresting hook after impacting

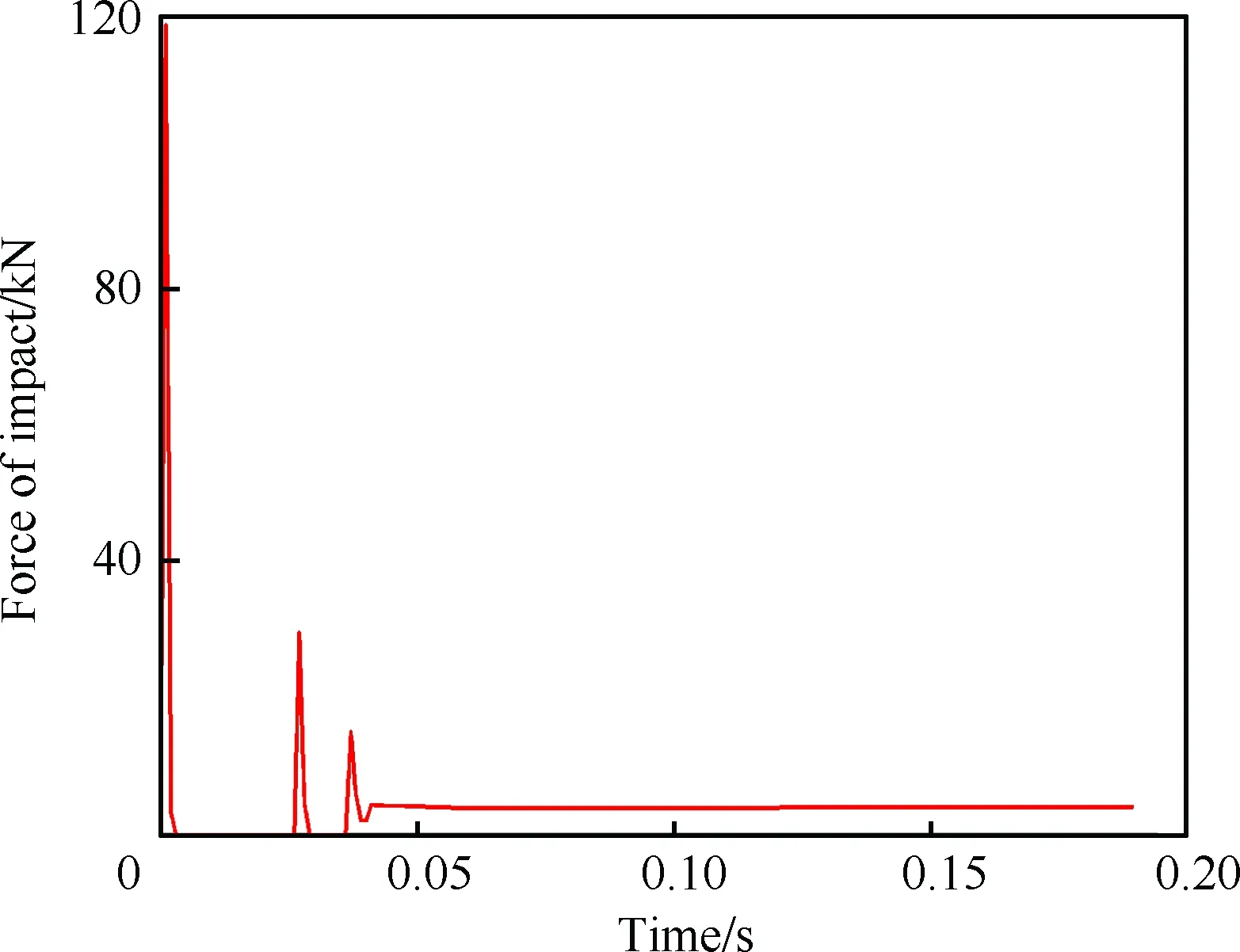
图12 拦阻钩与甲板的碰撞载荷变化Fig.12 Change of force of impact between arresting hook and deck

图13 拦阻钩阻尼器作用力Fig.13 Force of damper of arresting hook

5 结 论

针对舰载飞机着舰时拦阻钩碰撞甲板时的反弹问题，提出了一种结合虚拟样机技术和试验技术的研究方法，用拦阻钩碰撞反弹试验的结果修正本文拦阻钩动力学模型，得到一个比较准确的仿真模型，通过对仿真结果的综合分析表明：

1) 甲板涂层可以减小拦阻钩反弹高度、反弹距离、碰撞力以及阻尼器作用力，甲板有涂层时，拦阻钩的弹跳高度可降低43%，碰撞力可降低61.9%。

2) 舰载飞机着舰时航向速度对拦阻钩碰撞高度几乎没有影响，但是如果航向速度为0 m/s，弹跳高度会很小甚至为0 mm，碰撞力会高达1 100 kN。随着下沉速度的增大，反弹高度和碰撞力明显增大，最大下沉速度工况下的反弹高度、碰撞力以及阻尼器作用力是平均下沉速度工况下的2倍多。

3) 随着飞机着舰俯仰角由8°减小到0°，拦阻钩甲板角减小，碰撞反弹高度和阻尼器作用力也随之减小，反弹高度减小了34.6%，阻尼器作用力减小了37.1%。俯仰角的变化对碰撞力的影响相对较小，随着俯仰角的减小，碰撞力减小了19.1%。

4) 拦阻钩阻尼器参数的变化不会影响碰撞力，但是对碰撞反弹高度、反弹距离和拦阻钩阻尼器作用力都会产生明显的影响。碰撞反弹高度和距离随着阻尼器充气压力的增大而减小，阻尼器作用力反之；随着阻尼器油孔面积的增大而增大，阻尼力反之。在阻尼器参数的选择上需权衡它对反弹高度、反弹距离以及阻尼力三者的影响。

5) 本文综合考虑了航母实际情况和着舰边界条件，给出了一组最佳的参数组合，仿真结果表明该工况下拦阻钩的反弹可以很好地被抑制，有利于拦阻钩上索。因此，本文的仿真分析工作对着舰工况的优化设计具有一定的指导作用。

[1] 柳刚. 舰载飞机着舰拦阻钩碰撞及拦阻动力学研究[D]. 南京: 南京航空航天大学, 2009: 50-51.

LIU G. Investigation on arresting dynamics for carrier-based aircraft with consideration of arresting hook bounce[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009: 50-51 (in Chinese).

[2] 聂宏, 彭一明, 魏小辉, 等. 舰载飞机着舰拦阻动力学研究综述[J]. 航空学报, 2014, 35(1): 1-12.

NIE H, PENG Y M, WEI X H, et al. Overview of carrier-based aircraft arrested deck-landing dynamics[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 1-12 (in Chinese).

[3] THOMLINSON J. A study of the aircraft arresting-hook bounce problem: R. & M. No. 2980[R]. London: Her Majesty’s Stationery Office, 1957.

[4] Engineered Arresting Systems Corporation. Safety bulletin[R]. Plaisir Cedex: Engineering Arresting System Corporation, 2004.

[5] 柳刚, 聂宏. 拦阻钩初次碰撞道面反弹动力学[J]. 航空学报, 2009, 30(9): 1672-1677.

LIU G, NIE H. Dynamics of arresting hook bounce after initial touchdown and impacting with deck[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(9): 1672-1677 (in Chinese).

[6] 柳刚, 聂宏. 飞机拦阻钩碰撞动力学和拦阻钩纵向阻尼器性能[J]. 航空学报, 2009, 30(11): 2093-2099.

LIU G, NIE H. Dynamics of bounce of aircraft arresting hook impacting with deck and performance of arresting hook longitudinal damper[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(11): 2093-2099 (in Chinese).

[7] ZHU Q D, MENG X, ZHANG Z. Simulation research on motion law of arresting hook during landing[J]. Applied Mechanics and Materials, 2013, 300-301: 997-1002.

[8] 范学伟, 吴永康, 吴少波, 等.拦阻钩触舰反弹动态分析及缓冲性能研究[J]. 飞机设计, 2015, 35(1): 6-12.

FAN X W, WU Y K, WU S B, et al. A research on collision process of arresting hook and cushioning properties of the buffer[J]. Aircraft Design, 2015, 35(1): 6-12 (in Chinese).

[9] 杨全伟. 舰载飞机拦阻钩载荷实测方法研究[J]. 航空学报, 2015, 36(4): 1162-1168.

YANG Q W. Research on flight measurement method of a carrier-based aircraft hook loads[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(4): 1162-1168 (in Chinese).

[10] 洪嘉振. 计算多体系统动力学[M]. 北京: 高等教育出版社, 1999: 44-49.

HONG J Z. Computational dynamics of multibody system[M]. Beijing: Higher Education Press, 1999: 44-49 (in Chinese).

[11] 冯飞, 常正, 聂宏, 等. 飞机柔性对前起落架摆振的影响分析[J]. 航空学报, 2011, 32(12): 2227-2235.

FENG F, CHANG Z, NIE H, et al. Analysis of influence of aircraft flexibility on nose landing gear shimmy[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(12): 2227-2235 (in Chinese).

[12] 飞机设计手册总编委会. 飞机设计手册： 起飞着陆系统设计[M]. 北京: 航空工业出版社, 2002: 95-170.

The Chief Committee of Aircraft Design Manual. Aircraft design manual: Takeoff and landing system design[M]. Beijing: Aviation Industry Press, 2002: 95-170 (in Chinese).

[13] 诸德培. 摆振理论及防摆措施[M]． 北京: 国防工业出版社, 1984: 2-4, 20-24.

ZHU D P. Shimmy theory and anti-shimmy measure[M]. Beijing: National Defense Industry Press, 1984: 2-4, 20-24 (in Chinese).

[14] 冯飞. 起落架非线性摆振分岔分析[D]. 南京: 南京航空航天大学, 2014: 106-108.

FENG F. Bifurcation analysis of nonlinear shimmy of landing gear[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014: 106-108 (in Chinese).

[15] JOHNSON K L. Contact mechanics[M]. Cambridge: Cambridge University, 1985: 90-104.

[16] YOUNG W C, BUDYNAS R G. Roark’s formula for stress and strain[M]. New York: The McGraw Hill Companies, 2002: 702-705.

[17] 范钦珊. 理论力学[M]. 北京: 高等教育出版社, 2000: 406-413.

FAN Q S. Theoretical mechanics[M]. Beijing: Higher Education Press, 2000: 406-413 (in Chinese).

[18] 孙安媛, 黄沛天. 也谈完全非弹性碰撞和恢复系数[J]. 大学物理, 2001, 20(3): 9-14.

SUN A Y, HUANG P T. On the completely inelastic collision and the coefficient of restitution[J]. College Physics, 2001, 20(3): 9-14 (in Chinese).

[19] 罗明聪. 柔性梁与刚性地面碰撞动力学研究及仿真[D]. 南京: 南京理工大学, 2006: 36-37.

LUO M C. Dynamic simulation and research of impact between the flexible and rigid surface[D]. Nanjing: Nanjing University of Science and Technology, 2006: 36-37 (in Chinese).

[20] 中国人民解放军总装备部. 军用飞机结构强度规范第4部分： 地面载荷: GJB 67.4A—2008[S]. 北京: 中国人民解放军总装备部, 2008: 4-5.

The PLA General Armament Department. Military airplane structural strength specification Part 4: Ground loads: GJB 67.4A—2008[S]. Beijing: The PLA General Armament Department, 2008: 4-5 (in Chinese).

Dynamicsanalysisofarrestinghookbounceaftertouchdownandimpactingwithdeck

PENGYiming,NIEHong*

StateKeyLaboratoryofMechanicsandControlofMechanicalStructures,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

Inordertoresearchthedynamicperformanceofthearrestinghookaftertouchdownandimpactingwiththedeckwhentheaircraftisarrested,afull-aircraftassemblymodelofacertaintypeofaircraftisdevelopedtoconductdynamicssimulationofthelandingoftheaircraftcarrier.Themodelisupdatedwiththedataofarrestinghookbouncetest,andamoreaccuratemodelisobtained.Thesimulationresultsarecomparedwiththetestresults,andtheaccuracyofthedynamicsmodelisverified.Theimpactofthedeckcoating,pitchangle,engagingvelocity,sinkingvelocityandparametersofthearrestinghookdamperonthedynamicsperformanceofarrestinghookbounceisstudied.Theresultsshowthattheengagingvelocityhaslittleeffectonbounceheightandimpactforce.Thebounceheightandimpactforcegetlargerwiththeincreaseofthesinkingvelocityandpitchangle.Theparametersofhookdamperalmosthavenoeffectontheimpactforce,butobviouseffectonthebounceheight.

carrieraircraft;arrestinghook;impact;dynamics;damper

2017-03-13；Revised2017-04-12；Accepted2017-05-10；Publishedonline2017-05-220915

URL：http://hkxb.buaa.edu.cn/CN/html/20171121.html

s：NationalNaturalScienceFoundationofChina(11372129);ProjectFundedbythePriorityAcademicProgramDevelopmentofJiangsuHigherEducationInstitutions

.E-mailhnie@nuaa.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221233

V226

A

1000-6893(2017)11-221233-11

2017-03-13；退修日期2017-04-12；录用日期2017-05-10；< class="emphasis_bold">网络出版时间

时间：2017-05-220915

http://hkxb.buaa.edu.cn/CN/html/20171121.html

国家自然科学基金(11372129)；江苏高校优势学科建设工程资助项目

.E-mailhnie@nuaa.edu.cn

彭一明，聂宏．舰载飞机着舰时拦阻钩碰撞反弹动力学分析J. 航空学报,2017,38(11):221233.PENGYM,NIEH.DynamicsanalysisofarrestinghookbounceaftertouchdownandimpactingwithdeckJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):221233.

(责任编辑：徐晓)