基于AHP-SPA方法的民机修理级别确定综合分析模型

贾宝惠，于灵杰，蔺越国，卢翔

中国民航大学 航空工程学院，天津 300300

基于AHP-SPA方法的民机修理级别确定综合分析模型

贾宝惠*，于灵杰，蔺越国，卢翔

中国民航大学 航空工程学院，天津 300300

民机保障性分析中的重要内容之一是修理级别分析(Level of Repair Analysis, LORA)，现有的修理级别分析模型没有基于民机维修保障体制的特点综合考虑各类影响修理级别的因素。文章综合考虑修理级别分析的技术指标、经济指标和商业指标，将层次分析法(Analytical Hierarchy Process，AHP)与集对分析法(Set Pair Analysis，SPA)结合起来，建立民机修理级别分析综合评价模型，以实施经济性修理级别分析。并通过实例对AHP-SPA综合分析模型进行验证，表明了该模型的可行性，因此该文章的理论模型可为民机制造商和航空公司在修理级别确定方面提供理论参考和技术支持。

保障性分析；修理级别分析；层次分析法；集对分析法；综合评价模型

修理级别分析(Level of Repair Analysis， LORA)是在装备研制阶段根据装备修理的约定层次与修理级别的关系，分析确定装备中的产品故障或损坏时是需要报废或是需要修理，如需要修理，确定应在哪一个维修级别机构中完成修理工作是最佳的过程[1]。根据维修的不同深度、广度、技术复杂程度和维修资源等因素，将民用飞机修理级别分三级，即航线级、车间级和基地级[2]。在进行民机修理级别分析时，要考虑的因素包括非经济因素和经济因素两大方面。一级指标为商业性指标、技术性指标、经济性指标。二级基层指标有执行任务要求、保密性、效能、安全性、现有维修方案、PHST(Packaging，Handling and Stevedoring Transportation)、保障设备与设施、人力与人员、维修费用和维修时间等10个[3]，并针对定性指标和定量指标的特点分析了指标的评价标准。

近年来国内外十分重视修理级别分析的研究，2014年，美军采用工业标准SAE AS1390[4]，“LORA”给出了实施和执行修理级别分析活动的标准化方法；Barros先提出解决LORA问题的完整规划体系[5]，后和Riley提出了用确定的分支定界启发式算法，来解决LORA问题[6]；Gutina等通过在双向图上把LORA问题还原成二部图的最大权独立集问题证明了LOAR问题是多项式时间可解的[7-8]；Haritha和Kumar建立的优化模型是一个0-1线性规划问题[9]，假设任意一个部件负担一个特定固定成本，并通过一个航空发动机的修理级别实例分析，研究该算法在求解LORA问题上的应用；Basten等先后提出多层多级整数规划模型和最小成本流模型并作了相关扩展，但是建立该模型需要更多关于修理网络的信息，在产品寿命初期执行修理级别分析时很难获得该信息[10-12]；Brick和Uchoa在LORA问题中加入了修理设施选址问题[13]，增加了问题的复杂程度，作者不得不作简化假设，这里资源有容量限制，且数据不是按级别聚合。

中国对修理级别分析的研究开始较晚，但也进行了大量研究；吴昊等针对民机修理，建立层次化模型，将定性问题转化成定量问题，利用免疫粒子群优化(Immunity Algorithms-Particle Swarm Optimization,IA-PSO)算法对建立的优化模型进行优化求解，进行实例分析验证模型的合理性[14-15]；李鑫等在基于模糊层次分析法的基础上引入灰色关联分析，分别建立LORA经济性和非经济性分析模型[16-17];薛陶等先后基于LORA决策流、层次分析法和灰色关联度建立经济性分析模型，后来又构建了一个三层两级的非线性联合优化模型，所提出的联合优化方法可节约维修费用[18-20]。

国外对于修理级别分析的研究以降低全寿命周期维修费用为出发点，建立数学模型，并研究相关算法，以期对模型进行优化求解。国内修理级别分析方法科学性和可操作性较差。另外，现有的修理级别分析模型，没有综合考虑影响修理级别分析的因素和民机维修保障体制的特点。本文将层次分析法与集对分析法有机结合，综合考虑影响修理级别分析的技术性因素、经济性因素和商业性因素，建立民机修理级别分析综合评价模型。以某型民机升降舵伺服阀为研究对象，应用该模型对备选修理级别方案进行综合评价，确定该故障件的最佳修理级别，从而验证了该模型的合理性。

1 民机修理级别评价的指标权重确定方法

图1显示了层次分析法(Analytical Hierarchy Process，AHP)确定权重的流程。

由图1可知，首先要构造判断矩阵A，通过和法求解指标权重确定A的特征向量w,通过平均随机一致性指标计算一致性比例，以检验判断矩阵A的一致性，最终确定权重。

1.1 判断矩阵的建立依据

AHP[21]方法通过比较判断指标的相对重要性，判断矩阵利用标度将指标间的相对重要性定量化，通常使用Thomas提出的1～9标度衡量其关系，AHP的比例标度反映的是人们对定性因素的比较判断，一般不具有实际的物理意义，判断矩阵标度的含义如表1所示。

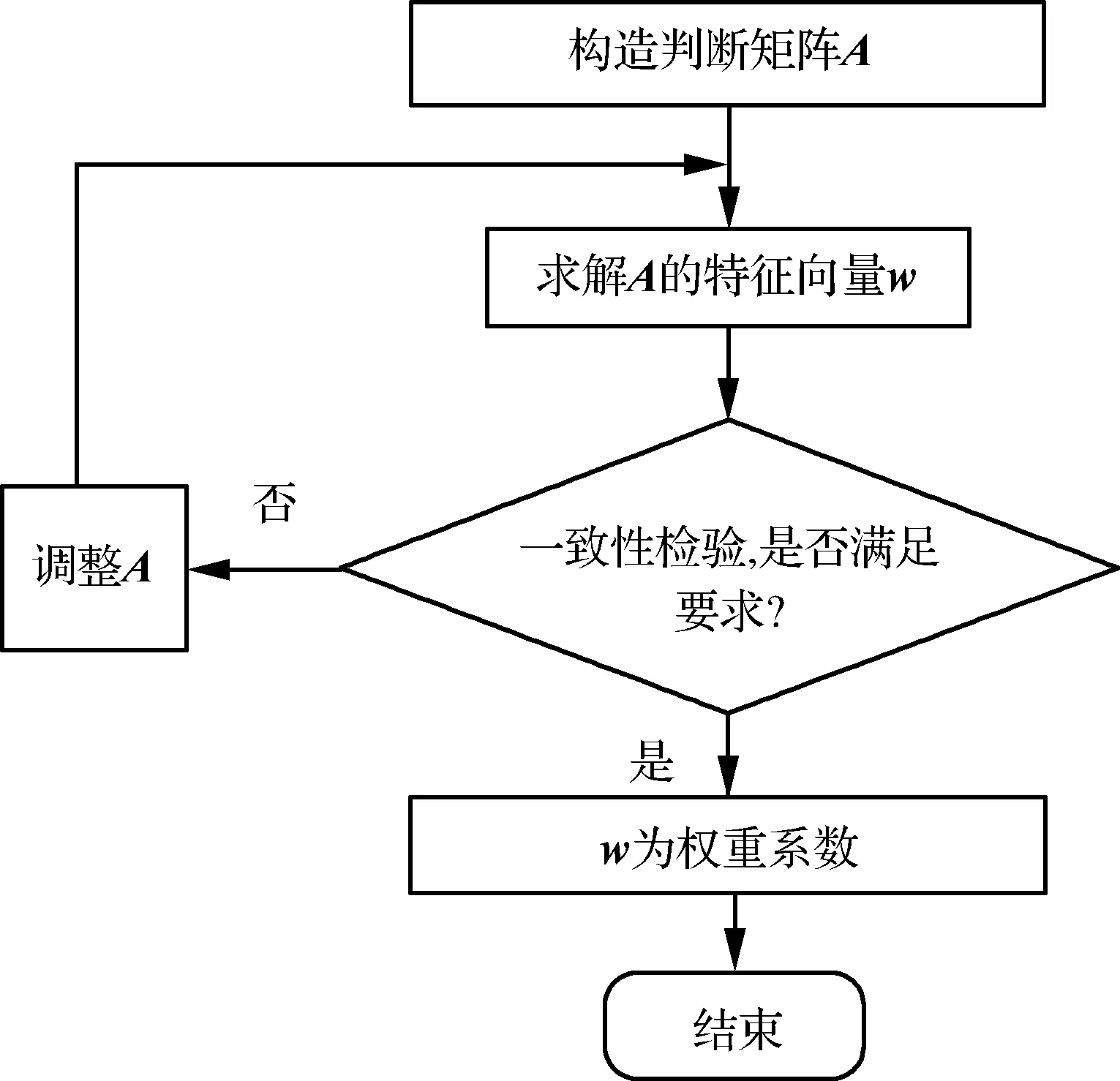
图1 层次分析法确定权重的流程Fig.1 Process of determining weight with AHP

表1 判断矩阵标度及其含义Table 1 Scale and meaning of judgment matrix

重要性标度含 义1表示两个元素相比，具有同等重要性3表示两个元素相比，前者比后者稍微重要5表示两个元素相比，前者比后者明显重要7表示两个元素相比，前者比后者强烈重要9表示两个元素相比，前者比后者极端重要2，4，6，8表示上述判断的中间情况倒数若元素i与元素j的重要性之比为bij，则元素j与元素i的重要性之比为bji=1/bij

1.2 指标权重的计算

求解判断矩阵的特征向量w，本文采用和法求解指标权重。

1) 将判断矩阵每一列归一化：

(1)

将按列归一化后的判断矩阵再按行求和：

(2)

(3)

则w=[w1,w2,…,wn]T即为所求的特征向量，即指标权重。

1.3 一致性检验及调整

设判断矩阵最大特征根为λmax:

(4)

式中：(Bw)i为向量Bw的第i个分量;n为判断矩阵阶数。

如果判断矩阵B具有完全一致性，λmax=n。但一般情况下B是近似估值，故有λmax≥n，因此可以用λmax与n的误差来判断B的准确性。为了检验判断矩阵的一致性，需要计算它的一致性指标CI:

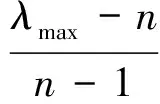
(5)

当判断矩阵具有完全一致性时，CI=0。设判断矩阵平均随机性一致性指标RI，对于不同阶数的判断矩阵，RI的值可查表得出。计算一致性比例CR：

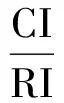
(6)

若CR计算值小于0.1，则判断矩阵通过检验，其一致性是可以接受的，否则重新调整判断矩阵。

2 综合评价方法

基于民机维修等级评价问题的工程实际特点，只需计算方案之间的同一度。一般说来，首先要进行评价的问题描述：设备选方案为D1,D2,…,Dp共p个。每个方案有E1,E2,…,Em共m个指标，各个指标的单位没有限制，可以一样，也可以不一样。eik(i=1,2,…,p;k=1,2,…,m)表示第i个方案、第k个指标的指标值[22]。在进行方案综合评价之前，要进行指标权重的确定。对各备选方案进行综合评价，做出决策。为了解决上述问题，应用基于集对分析法(Set Pair Analysis, SPA)同一度的综合评价方法，其步骤如下：

1) 建立综合分析模型描述要解决的问题

建立方案模型，描述要解决的问题。基于集合的概念，通常将所分析的问题表示为一个集合。集合由各个子集组成，包括备选方案集、评价指标集、指标权重集、集对矩阵集以及联系矩阵集等。

2) 确定理想方案

建立理想方案T,作为评价的基准，理想方案的第k个指标值为e0k。

3) 计算指标值间的同一度

计算备选方案与理想方案各指标值之间的同一度，设同一度值为aik,则有

(7)

4) 计算方案间的同一度

计算各个备选方案与理想方案之间的同一度，设同一度值为ai(i=1,2,…,p)。由步骤3)计算得到各指标之间的同一度aik,再已知各指标的权重wk(k=1,2,…,m),便可加权得到各备选方案与理想方案之间的同一度：

(8)

5) 确定最优方案

根据步骤4)计算得到方案间的同一度值ai,同一度值最大的备选方案即为最优方案。

D*=max(a1,a2,…,an)

(9)

具体流程如图2所示。

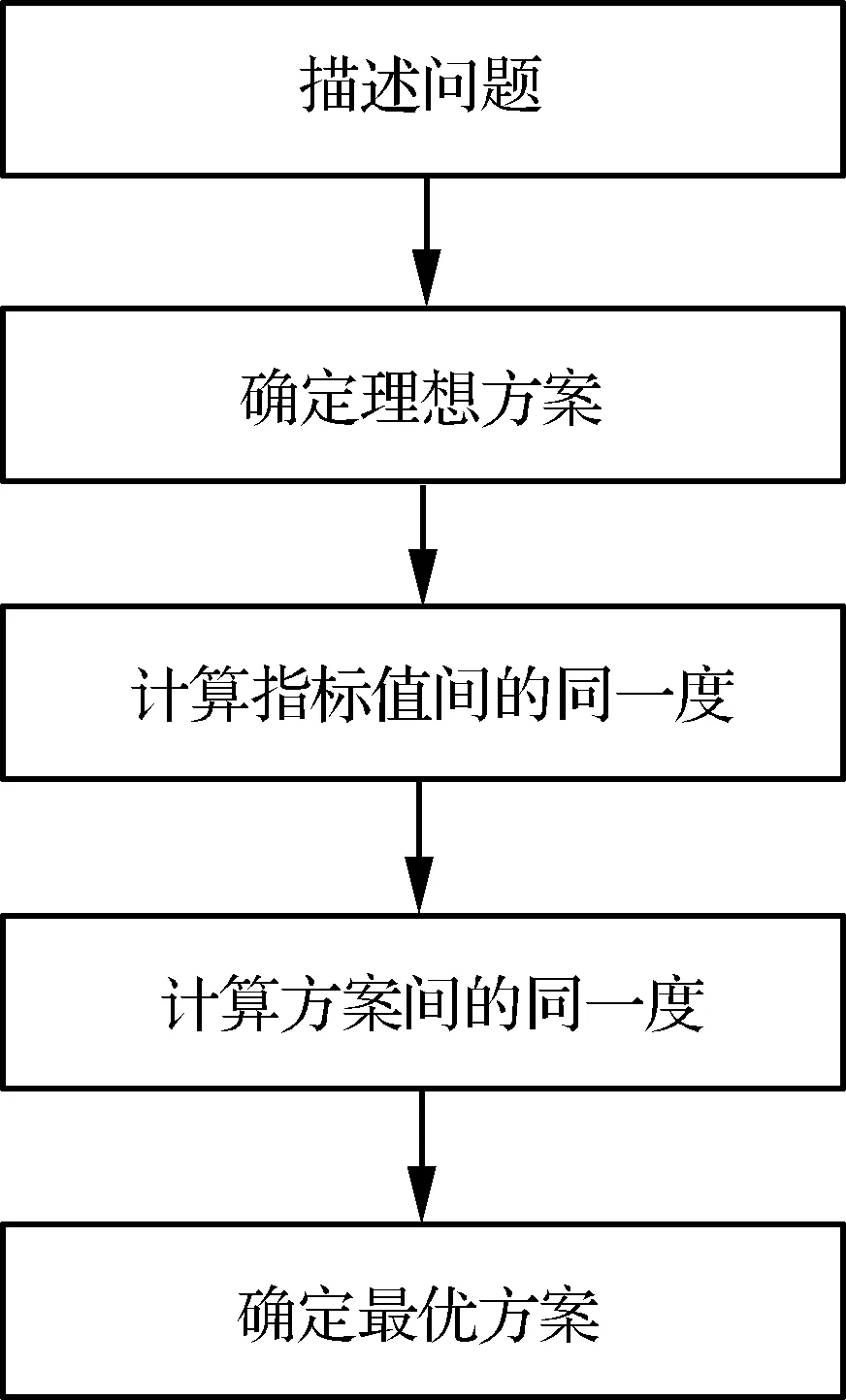
图2 基于SPA同一度的综合评价流程Fig.2 Comprehensive evaluation process based on SPA same degree

3 建立综合评价模型

本文采用层次分析法来确定指标权重，用集对分析法进行综合评价，建立了民机修理级别综合评价模型，对备选维修方案进行评价比较。

首先,建立评价指标体系：通过对相关领域专家的意见征询，综合分析后，建立修理级别分析评价综合指标体系，一级指标为商业性指标、技术性指标、经济性指标。其中商业性指标和技术性指标是对非经济性因素的拆分。根据一级指标对修理级别方案的影响划分二级指标，如商业性指标包括执行任务要求、保密性、维修时间3个影响因素。本文建立的民机修理级别综合评价指标体系如图3所示。

其次，对各个指标进行评分：对于执行任务要求、保密性、效能、安全性、现有维修方案、PHST、保障设备与设施、人力与人员等定性指标，设立评价集，用{好，较好，一般，较差，差}五级评语评定指标。汇总专家评价表，各指标的最终得分是专家评价的均值。具体方法参照以下步骤进行：

1) 列举各影响因素，并罗列出修理级别备选方案。

图3 修理级别分析评价指标体系Fig.3 Repair level analysis and evaluation index system

2) 制作定性指标评价表，如表2所示,表中O为航线级;I为车间级;D为基地级;X为报废。采用置信度的形式，对各指标的评价等级进行评价。置信度以小数表示，且各指标的评价等级打分之和不能大于1。

3) 为了减弱评价过程中的主观影响，可聘请多位专业人员，进行多轮评价，对评价结果进行综合分析计算，得表3。

维修费用和维修时间为定量指标，取其实际值作为评价值。维修费用利用维修成本数据进行计算，计算方法参考贾宝惠和周帆的最小成本优化模型[23]，其中对于各类费用的计算公式以及基本费用参数的计算方法可参考GJB 2961-97[24]。文献[23]中最小成本优化模型为

(10)

式中：l为所研究系统的部件总数；r为修理选项,修理、报废或移动；γx为部件x全寿命周期内所需维修任务的总次数；FCr,e,x为部件x在维修级别e上执行修理选项r的固定成本；VCr,e,x为部件x在维修级别e上执行修理选项r的可变成本；决策变量Xr,e,x=1为部件x在修理级别e上选择了修理选项r,否则Xr,e,x=0;修理级别e=1代表航线级，e=2代表车间级，e=3代表基地级。

表2 定性评价指标Table 2 Qualitative evaluation index

表3 民机修理级别分析综合评价层次结构模型

第三，对各指标评分确定权重：确定权重的计算方法如式(1)～式(6)；利用集对分析法依次计算指标间和方案间的同一度，如式(7)～式(9)，最终确定最优方案，具体流程如图4所示。

4 实例分析

以某型民机升降舵伺服阀为研究对象，对该故障件进行修理级别分析，该型飞机每个升降舵伺服控制器有一个伺服阀(SV)，如图5所示。

升降舵伺服阀控制原理如图6所示,当计算机ELAC2、ELAC1、SEC2和SEC1都处在正常工作状态时，伺服阀由计算机控制，以作动升降舵。

汇总该研究对象的专家评价定性指标值、据式(10)计算的维修费用以及维修时间的实际值。表4给出了各方案对应的指标值。

基于AHP法，构造判断矩阵A、B1、B2、B3,根据式(1)～式(6)，计算可得各级指标权重wi:

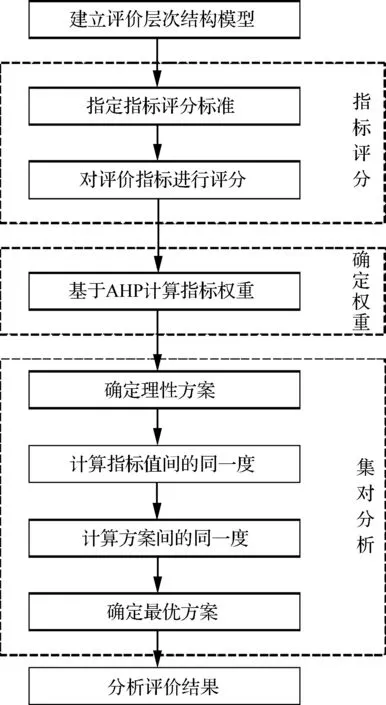
图4 基于AHP-SPA的民机修理级别分析 综合评价模型Fig.4 Aircraft repair level analysis comprehensive evaluation model based on AHP-SPA

图5 升降舵伺服控制器主要结构组成Fig.5 Main structure of elevator servo controller

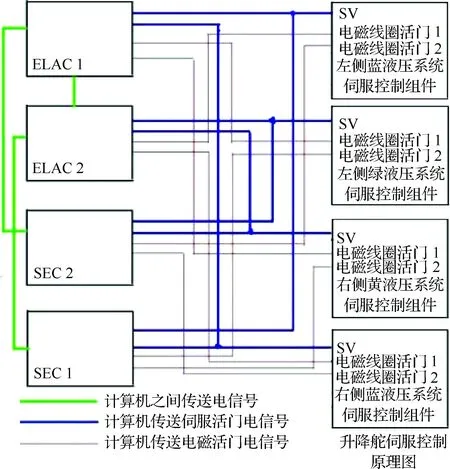
图6 升降舵伺服控制原理图Fig.6 Elevator servo control schematic

表4 评价指标值Table 4 Evaluation index value

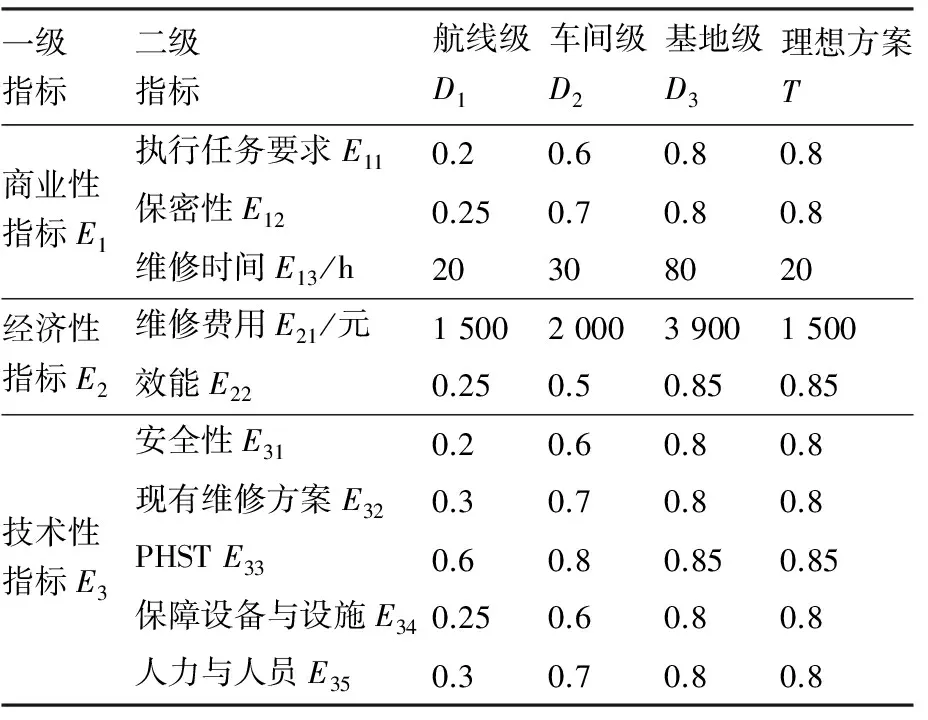
一级指标二级指标航线级D1车间级D2基地级D3理想方案T商业性指标E1执行任务要求E110．20．60．80．8保密性E120．250．70．80．8维修时间E13/h20308020经济性指标E2维修费用E21/元1500200039001500效能E220．250．50．850．85技术性指标E3安全性E310．20．60．80．8现有维修方案E320．30．70．80．8PHSTE330．60．80．850．85保障设备与设施E340．250．60．80．8人力与人员E350．30．70．80．8

(11)

(12)

(13)

(14)

一级指标权重分别为

1) 一级指标商业性因素的权重为w1=0.198；

2) 一级指标经济性因素的权重为w2=0.49；

3) 一级指标技术性因素的权重为w3=0.312。

二级指标权重分别为

1) 执行任务要求的权重为w11=0.346；

2) 保密性的权重为w12=0.11；

3) 维修时间的权重为w13=0.544；

4) 维修费用的权重为w21=0.5；

5) 效能的权重为w22=0.5；

6) 安全性的权重为w31=0.109；

7) 现有维修方案的权重为w32=0.109；

8) PHST的权重为w33=0.207；

9) 保障设备与设施的权重为w34=0.368；

10) 人力与人员的权重为w35=0.207。

建立理想方案T，作为评价的基准。由表4可得，理想方案各指标值为

T={0.8,0.8,20,1 500,0.85,0.8,0.8,0.85,

0.8,0.8}

由式(7)，可得同一度矩阵

(15)

计算一级指标间的同一度s1、s2、s3。根据式(8)和式(15)，可得s1=a11w11+a12w12+a13w13=0.665,其余同理计算，可得：

方案D1:{s1,s2,s3}={0.665,0.656,0.407};

方案D2:{s1,s2,s3}={0.718,0.669,0.829};

方案D3:{s1,s2,s3}={0.592,0.693,1.000}。

得到3个方案一级指标间同一度对比图，由图7知：方案D2、D3技术性指标的同一度明显高于其余指标，3个方案的商业性指标和经济性指标同一度大致相当。

再根据式(8)和式(11)计算方案同一度a1、a2、a3,得出a1=s1w1+s2w2+s3w3=0.58,其余同理计算，可得：ai={0.58,0.729,0.769}。

计算得到方案间的同一度值ai对比如图8所示：方案D3的同一度明显高于其余二者，最终采用方案D3作为最佳修理方案，即基地级。

图7 3个方案中一级指标同一度对比图Fig.7 Comparison of the first index and the same degree in three schemes

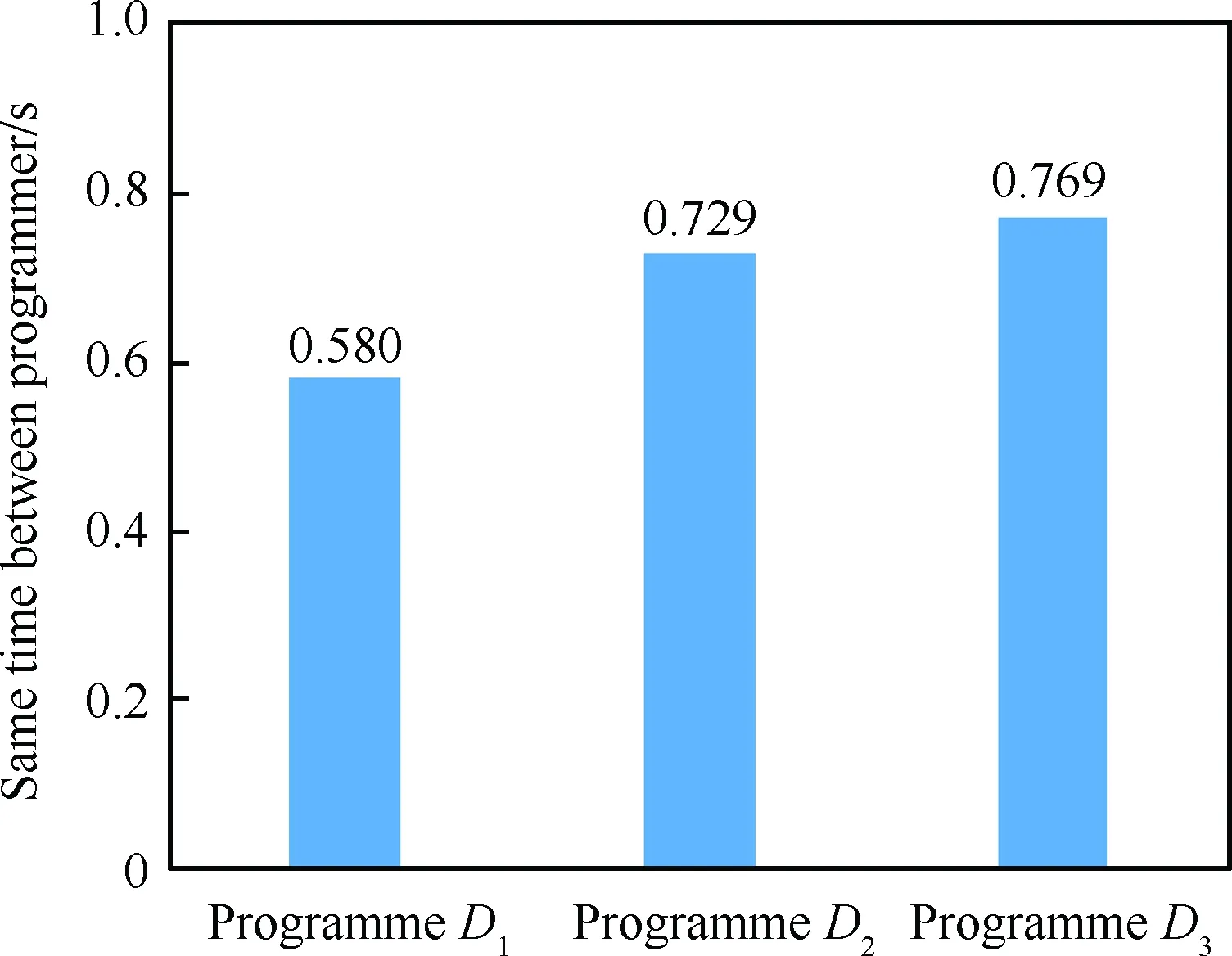
图8 3个方案的同一度对比图Fig.8 Comparison of the same degree of three schemes

5 结 论

1) 建立了基于AHP-SPA的民机修理级别分析综合评价模型，并详细推导建模过程，该模型基于AHP来确定指标权重，然后选择SPA作为综合评价方法，可对修理级别备选方案进行定量评估，并实施有效的经济性修理级别分析。

2) 利用AHP-SPA综合评价模型对某型民机升降舵伺服阀进行修理级别确定，通过建立判断矩阵，得到各级指标权重，以理想方案各指标权重作为评价基准，计算各级指标同一度进而得到三个方案的同一度，最终确定基地级为最佳修理方案，该结果与实际情况吻合。

3) 通过实例分析验证了所建模型的合理性，给出最优备选维修方案，本文的方法更加准确有效，从而完善了民机修理级别分析理论，增强了开展修理级别分析工作的可操作性，特别是解决民机设计和维修规划问题极为有效。

[1] 魏效燕, 刘晓东. 基于AHP方法的军用飞机修理级别分析[J]. 航空维修与工程，2006(2)：22-24.

WEI X Y，LIU X D.Military aircraft’s level of repair analysis which based on AHP[J].Aviation Maintenance，2006(2):22-24(in Chinese).

[2] 吴昊. 民用飞机规划维修技术理论及应用研究[D].南京：南京航空航天大学，2009：71-75.

WU H.Research on theory and application of civil aircraft maintenance planning[D].Nanjing:Nanjing University of Aeronautics and Astronautics，2009:71-75(in Chinese).

[3] Aerospace and Defense Industries Association of Europe.S3000L international procedure specification logistics support analysis[S]. Brussels: Aerospace and Defense Industries Association of Europe ,2010 :4.

[4] SAE. AS1390: Level of repair analysis (LORA)[S].Warrendale :SAE International,2014.

[5] BARROS L L. The optimization of repair decision using life-cycle cost Parameters[J]. IMA Journal of Management Mathematics，1998，9(4)：403-413.

[6] BARROS L，RILEY M. A combinatorial approach to level of repair analysis [J]. European Journal of Operational Research，2001，129(2)：242-251.

[7] GUTINA G,RAFIEY A,YEO A.Graph-theoretical approach to level of repair analysis [EB/OL].2004.(2017-01-12)[2017-01-13].http∥www.optimization online. org/DB_FILE/2004/08/945. pdf. /2007-11-28.

[8] GUTINA G，RAFIEY A，YEO A，et al. Level of repair analysis and minimum cost homomorphisms of graphs[J]. Discrete Applied Mathematics，2006，154(6)：881-889.

[9] HARITHA S, KUMAR U D. Optimization of aircraft maintenance/support infrastructure using genetic algorithms-level of repair analysis[J].Annals of Operations Research，2006，143：91-106.

[10] BASTEN R J I，SCHUTTEN J M J，HEIJDEN M C. An efficient model formulation for level of repair analysis[J]. Annals of Operations Research，2009，172(1)：119-142.

[11] BASTEN R J I，HEIJDEN M C，SCHUTTEN J M J. A minimum cost flow model for level of repair analysis[J]. International Journal of Production Economics，2011，133(1)：233-242.

[12] BASTEN R J I，HEIJDEN M C，SCHUTTEN J M J. Practical extensions to a minimum cost flow model for level of repair analysis[J]. European Journal of Operational Research，2011，211(2)：333-342.

[13] BRICK E S，UCHOA E. A facility location and installation of resources model for level of repair analysis[J]. European Journal of Operational Research，2007，192(2)：479-486.

[14] 吴昊, 左洪福.基于改进层次分析法的民用飞机修理级别非经济性分析[J]. 飞机设计，2008，28(6):46-49.

WU H，ZUO H F.Level of repair analysis non-ecomonic evaluation for aircraft maintenance based on improved AHP[J].Aircraft Design，2008，28(6):46-49(in Chinese).

[15] 吴昊, 左洪福, 孙伟.一种新的民用飞机修理级别优化模型[J]. 航空学报，2009，30(2):247-253.

WU H，ZUO H F，SUN W.A new level of repair analysis optimization model for civil aircraft maintenance[J].Acta Aeronautica et Astronautica Sinica，2009，30(2):247-253(in Chinese).

[16] 李鑫, 蔡景, 左洪福, 等.基于改进FAHP的民机修理级别经济性分析研究[J]. 四川兵工学报，2014，35(6)：64-67.

LI X，CAI J，ZUO H F，et al.Level of repair analysis economic evaluation for aircraft maintenance based on improved FAHP[J].Journal of Sichuan Ordnance，2014，35(6)：64-67(in Chinese).

[17] 李鑫, 蔡景, 左洪福, 等.两级修理模式下民机修理级别非经济性分析研究[J].火力与指挥控制，2015，40(7)：8-11.

LI X，CAI J，ZUO H F，et al.Research on level of repair analysis non-economic evaluation for civil aircraft maintenance based on two-level maintenance[J].Fire Control&Command Control，2015，40(7)：8-11(in Chinese).

[18] 薛陶, 冯蕴雯, 薛小锋,等.一种飞机修理级别经济性分析模型[J]. 航空学报，2013，34(1):97-103.

XUE T，FENG Y W，XUE X F，et al.An analysis economic evaluation model for level of repair analysis[J].Acta Aeronautica et Astronautica Sinica，2013，34(1):97-103(in Chinese).

[19] 薛陶, 冯蕴雯, 代晓明. 基于改进AHP方法的飞机修理级别经济性分析[J]. 火力与指挥控制，2013，38(3)：58-61.

XUE T，FENG Y W，DAI X M.Level of repair analysis economic evaluation for aircraft maintenance based on improved AHP[J].Fire Control&Command Control，2013，38(3)：58-61(in Chinese).

[20] 薛陶，冯蕴雯, 薛小锋.装备修理级别与备件库存联合优化模型研究[J].机械科学与技术，2015，34(6)：963-968.

XUE T，FENG Y W，XUE X F.Research on joint optimizing model of equipment LORA and spare parts inventory[J].Mechanical Science and Technology for Aerospace Engineering，2015，34(6)：963-968(in Chinese).

[21] 赵焕臣.层次分析法[M].北京：科学出版社，1986：85-96.

ZHAO H C.Analytic hierarchy process[M].Beijing：Science Press，1986：85-96 (in Chinese).

[22] 赵克勤.基于集对分析同一度的方案综合评价决策[J].决策探索，1994，2：14-15.

ZHAO K Q.Comprehensive evaluation for decision of the plan based on identical degree of the set pair analysis[J].Decision to Explore，1994，2：14-15 (in Chinese).

[23] 贾宝惠，周帆.基于遗传禁忌搜索混合算法的修理级别问题研究[J].机械工程与自动化，2015，6：11-16.

JIA B H，ZHOU F.Study on level of repair analysis based on hybrid genetic-tabu search algorithm[J].Mechnical Engineering&Automation，2015，6：11-16 (in Chinese).

[24] 中国航空综合技术研究所.GJB 2961-97 修理级别分析[S]. 北京：国防科工委军标出版发行部，1997.

AVIC China Aero-polytechnology Establishment.GJB 2961-97 Level of repair analysis[S].Beijing：Military Standard Publishing Department of Commission of Science Technology and Industry for National Defense, 1997 (in Chinese).

ComprehensiveanalysismodelfordeterminationofcivilaircraftrepairlevelbasedonAHP-SPAmethod

JIABaohui*,YULingjie,LINYueguo,LUXiang

CollegeofAviationEngineering,CivilAviationUniversityofChina,Tianjin300300,China

OneoftheimportantcontentsofcivilaircraftsecurityanalysisisLevelofRepairAnalysis(LORA).Theexistinglevelofrepairanalysismodelisnotbasedonthecharacteristicsofcivilaircraftmaintenancesafeguardsystemtotakeintoconsiderationvariousfactorsaffectingthelevelofrepair.Inthispaper,theAHP(AnalyticalHierarchyProcess)iscombinedwithSPA(SetPairAnalysis)bycomprehensivelyconsideringthetechnicalindex,economicindexandbusinessindexofLevelofrepairanalysissoastoestablishthecomprehensiveevaluationmodelforcivilaircraftlevelofrepairanalysis,thusimplementingtheeconomiclevelofrepairanalysis.ThecomprehensiveanalysismodelofAHP-SPAisverifiedbyanexample,whichshowsthefeasibilityofthemodel.Therefore,thetheoreticalmodelofthispapercanprovidecivilaircraftmanufacturersandairlineswiththeoreticalreferenceandtechnicalsupportinthedeterminationoflevelofrepair.

securityanalysis;levelofrepairanalysis;analyticalhierarchyprocess;setpairanalysis;comprehensiveevaluationmodel

2017-01-13；Revised2017-03-19；Accepted2017-03-30;Publishedonline2017-04-200923

URL：http://hkxb.buaa.edu.cn/CN/html/20171117.html

MajorProjectFoundationofCivilAviationAdministrationofChina(MHRD20160105)

.E-mail15510928918@163.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.221130

V267

A

1000-6893(2017)11-221130-09

2017-01-13；退修日期2017-03-19；录用日期2017-03-30;< class="emphasis_bold">网络出版时间

时间：2017-04-200923

http://hkxb.buaa.edu.cn/CN/html/20171117.html

中国民航局重大专项(MHRD20160105)

.E-mail15510928918@163.com

贾宝惠，于灵杰，蔺越国，等．基于AHP-SPA方法的民机修理级别确定综合分析模型J．航空学报,2017,38(11):221130.JIABH,YULJ,LINYG,etal.ComprehensiveanalysismodelfordeterminationofcivilaircraftrepairlevelbasedonAHP-SPAmethodJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):221130.

(责任编辑：张晗)