基于三方动态博弈模型的网络生存防御策略优化配置

伍 文，杨发亮，张兆忠，刘长乐

（解放军93936部队，银川 750025）

基于三方动态博弈模型的网络生存防御策略优化配置

伍 文，杨发亮，张兆忠，刘长乐

（解放军93936部队，银川 750025）

针对网络攻防环境中防御方以提高系统生存能力为目的所进行的最优生存防御策略的选取问题，提出了一种基于完全信息动态博弈理论的生存防御策略优化配置算法。将恶意攻击方、故障意外事件及防御方作为博弈的参与人，提出了一种混合战略模式下的三方动态博弈模型，对博弈的主要信息要素进行了说明，以混合战略纳什均衡理论为基础，将原纳什均衡条件式的表达式转化为可计算数值结果的表达式，并据此增加了近似的概念，最后，将提出的模型和近似纳什均衡求解算法应用到一个网络实例中，结果证明了模型和算法的可行性和有效性。

网络可生存性，策略选取，动态博弈，纳什均衡，粒子群

0 引言

计算机网络在金融、医疗、交通、军事、通信等领域发挥重大作用的同时，也遭受着来自各方面的威胁。各种网络安全、生存技术被开发以提高系统抵御威胁的能力。已有的可生存技术有IP重路由、服务动态配置、冗余、备份等［1］。但这些技术主要是针对威胁的、被动的、孤立的防御策略，没有形成统一战线；依赖人为选取策略，时效性低，也没有综合考虑成本因素；且部分技术功能交叉，造成了资源的浪费［2］。总之缺乏一套行之有效的统一调配机制使得这些技术的功能得到最大发挥。网络生存防御策略优化配置算法，是从策略层面考虑的生存防御措施，能够利用已有的安全及可生存性技术，动态优化配置网络的各种生存资源，有效提高网络的主动防御能力［3-4］。

文献［5］将故障、意外事件作为非理性攻击者纳入到博弈体系中，与攻击者、防御者共同构成博弈的参与方，建立一种三方完全信息生存动态博弈模型，提出了网络生存防御纯策略优化配置算法。本文在此基础之上，给出了一种网络生存防御混合策略优化配置算法。混合策略情况下，动态博弈参与人不是确定地选择行动空间中的某一策略，而是以一定的概率选择该策略予以指导行动。选择混合策略的目的是给其他参与人造成不确定性，这样尽管其他参与人知道选择某个特定纯策略的概率是多少，但是并不能猜透实际上会选择哪个纯策略。混合策略相比纯策略在应用上更具灵活性。

1 三方动态博弈模型的建立

建立的三方动态博弈模型如图1所示，

A.参与人：三方博弈参与者为攻击者、故障意外事件及防御者。攻击者指人为恶意攻击一方，具备分析决策能力，可理性判断应该采取的行动。故障意外事件为非理性攻击者，发生具有随机性，服从一定的分布，不具备理性分析能力。作为特殊的博弈参与人，故障意外事件是由外在自然触发，以触发概率值作为输入。防御者则通过实施各种防御策略达到对网络保护的目的。

B.行动次序：动态博弈参与人的行动次序是序贯的，各参与人依次采取行动。不同的行动顺序会产生不同的博弈结果。根据各参与人的决策顺序确定博弈模型的行动次序。

C.行动空间：行动空间是依据参与人的策略集，在每一个行动点的可选行动集。三方博弈中，对于攻击者，在攻击初始的行动空间AAo包括攻击者可选的攻击类型，可选的攻击对象等，在攻击进行中的行动空间AAg包括继续攻击、停止攻击、停留观察等策略；对于防御方的行动空间AS包括防御者针对各种攻击的容忍、恢复等策略；对于故障、意外事件，其行动空间AFo包括故障、意外事件的类型、位置等信息，AFg包括继续破坏、停止破坏等信息，与攻击者不同的是，其行动空间是非理性的，具体行动由故障、意外造成的实际影响确定。

D.信息集：博弈理论中信息是参与人有关其他参与人特征和行动的知识。根据博弈参与人所掌握的信息，将博弈扩展式上的所有决策结分割成不同的集合，这些集合称为信息集，对一个参与人的同一个信息集，后一个参与人无法区分博弈进入该集合的哪一个决策结。对于完美信息动态博弈，信息集都是单点集［6］。

E.收益：在动态博弈中，收益是指在特定的序贯行动组合下参与人得到的效用水平。收益量化是博弈中一个非常重要的问题，其准确性直接决定博弈结果的准确性。混合战略动态博弈参与人的收益是参与人纯策略收益组成的期望收益，下面给出计算方法［7］。

其中，φ为所有路径组成的集合。

这里需要说明一下的是，三方动态博弈模型中，攻击者的收益包括攻击者的自身收益和非理性攻击者的额外收益。故障意外事件是由自然触发的，不以获得收益为目的。

F.扩展式表示：动态博弈扩展式是以树型结构将动态博弈过程形象直观地表示出来。给出三方博弈的扩展式示意图如图2所示，“1”表示故障，“2”表示攻击者，“3”表示防御者。

2 混合战略纳什均衡及其计算形式

有限n人非合作混合战略动态博弈中［8］，混合战略组合是一个纳什均衡，如果对于所有的 i=1，2，…，n，满足：

式（2）给出的纳什均衡定义是以条件的方式给出。对于一个复杂的博弈问题，给出一个结果可轻易判断该结果是否为纳什均衡值，但是难以从式（2）直接求解得到纳什均衡值。因此，首先将式（2）转化为易于计算的形式。

式（3）将得到一个确定的值，而非式（2）中仅为一个判定过程。

式（4）是以一定的近似找到接近纳什均衡的一组解，近似程度根据实际需要确定，近似程度由γ确定，γ越大，越接近纳什均衡，当γ=100时，得到的γ%近似纳什均衡与式（3）给出的纳什均衡一致。

采用粒子群算法对提出的三方动态模型进行求解，具体求解过程在文献［9］中已经做过描述，这里不再赘述。

3 实例分析

采用如图3所示的网络环境进行模拟实验分析。

理性攻击者通过外网对内网的各个节点进行攻击，以破坏内部网络的可用性作为目的，内网布置有各种生存措施阻挡外来威胁对系统网络造成的伤害，非理性攻击者（例如，软硬件故障）的发生是随机，可人为统计其概率数据。三方动态博弈模型的建立是以网络在容忍、恢复阶段的生存对抗为背景的（将网络的生存过程分为抵抗，检测，容忍恢复3个阶段）。对博弈参与者策略的分析如表1所示：

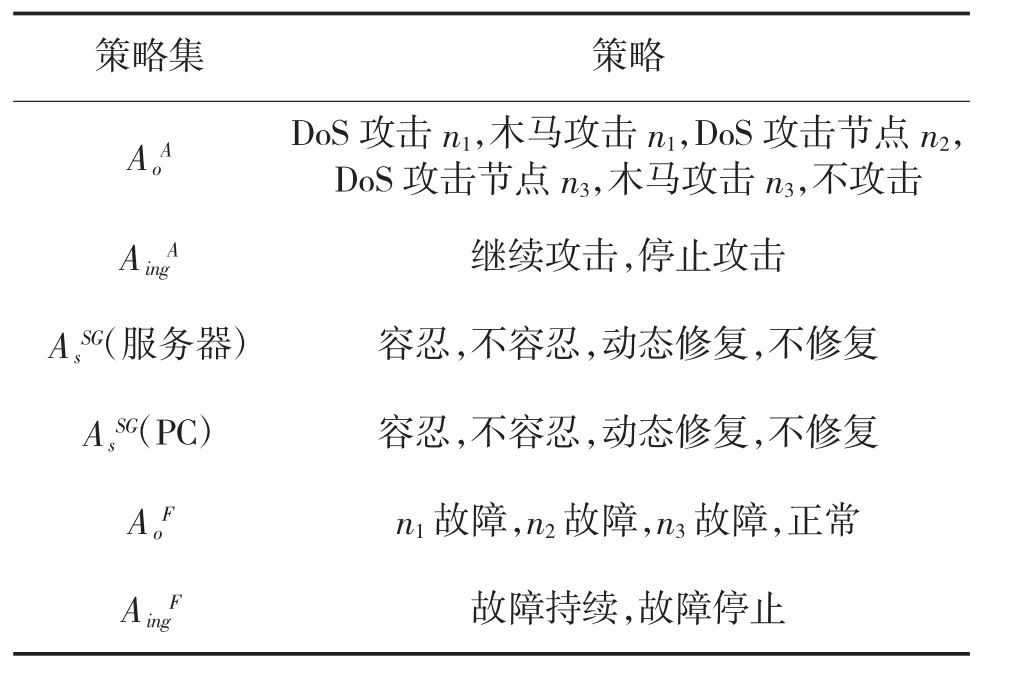
表1 参与者策略表

3.1 单个攻击对象的模型建立及纳什均衡结果分析

首先以网络中单个设备为研究对象来构建三方动态博弈模型和进行混合战略纳什均衡的计算。针对图3中节点1Web服务器，某管理员在了解各方策略的前提下，设计了攻击者、防御者及故障事件的三方动态博弈模型如下页图4所示，根据其经验给出了各博弈路径的攻防双方的收益值。该模型分为两个部分，用虚线分开，虚线上和虚线下的部分分别为Web服务器故障和无故障情况下的动态博弈模型。在后续的仿真中，将分别计算两种情况下的近似纳什均衡。

下页图4中，加方框的决策结为理性攻击者与防御者需要做决策的点，与其连接的后续行动被选取的概率值即为混合战略纳什均衡的求解对象，这些决策结分别被标识为a～e，其后续行动的概率值分别表示为σa1、σa2、σb1、σb2......，以此类推（见图 4）。其中σx1+σx2=1，x表示a～e。未加方框的决策结包含两种情况，一种为故障意外事件，其行动策略的概率值是在算法运行前根据实际掌握数据给定；一种为理性攻击者，但其后续行动只有一个。

首先计算Web服务器无故障情况下的纳什均衡，设置仿真参数 c1=c2=1，ωmax=0.9，ωmin=0.6，取粒子群规模m=10，根据文献［9］中的算法计算得到纳什均衡结果为：

对图4进行分析，观察其收益函数，不论在什么情况下，理性攻击者采取DoS攻击、继续攻击均会得到相比其他策略更高的收益，因此没有理由选取其他策略而放弃策略DoS攻击和继续攻击；同理，防御者没有理由不选取容忍和动态修复策略，双方均会以更可能高的概率（概率值为1）来选择这4个策略。因此，分析得到的纳什均衡结果与纳什均衡求解算法计算得到的纳什均衡一致，该仿真验证了基于粒子群的纳什均衡求解算法的正确性。

在获知纳什均衡结果的前提下，对Web服务器无故障情况下的γ%近似纳什均衡进行分析，图5给出了近似程度γ随迭代次数增加的变化过程。

迭代次数在25次以下时，γ的值起伏比较大，但整体趋势向纳什均衡点靠近；当迭代次数在25～43次之间时，γ的值明显趋近纳什均衡点，但结果不稳定，将该阶段称为γ%近似伪纳什均衡阶段，该阶段γ最小的取值γmin=97.94，最大值γmax=100，平均值γavg=99.65，可以看出该阶段的纳什均衡结果已经非常近似真正的纳什均衡结果；当迭代次数在43次以上时，γ已经很稳定地取值为100，该阶段计算得到的数值结果即为纳什均衡结果。经过比对γ%近似纳什均衡阶段和纳什均衡阶段的数值可以得出：γ%近似纳什均衡可以以更小的代价得到一近似纳什均衡结果，该结果与纳什均衡非常接近，与真实的纳什均衡具有相同的应用价值。

图6给出了程序运行时间随着迭代次数的变化趋势，从图6可以看出，随着迭代次数的递增，计算纳什均衡消耗的时间也不断增加，在γ%近似伪纳什均衡阶段，需要消耗的最少时间ta=1.964 0 s，而在纳什均衡阶段，需要消耗的最少时间tb=3.699 5 s。计算γ%近似纳什均衡相比计算纳什均衡时间节省了约为一半。

在图5中γ%近似伪纳什均衡阶段选取4组纳什均衡结果在图7中表示出来，从图中可以看出这4组值均非常接近真实的纳什均衡结果。因此，γ%近似纳什均衡概念的提出在确保结果有效的前提下节省了计算资源，这在实际网络策略选择应用中节省了决策时间，使得决策反映速度得到了提高。

当收益计算过程考虑的因素更加复杂，例如增加代价的计算，而不是仅仅行动即获益的思路，那么通过分析是无法获知纳什均衡结果的，而要依赖复杂的算法来求解。在Web服务器有故障情况的纳什均衡计算中，考虑该情况。

在Web服务器有故障情况下的纳什均衡计算中，粒子群算法的仿真参数与无故障情况下相同，迭代进行60次，得到4组不同故障场景下的纳什均衡仿真结果如表2所示。

表2中，当故障持续概率为100%时，攻击方将选择分别以100%和73.07%的概率选择DoS攻击n1和继续攻击策略，防御方将分别以100%和75%的概率选择容忍和动态修复策略，此时该近似纳什均衡结果以99.99%的近似程度近似于纳什均衡。当故障持续概率降为80%，DoS攻击n1的概率σa1与防御方容忍的概率σc1几乎保持不变，而继续攻击的概率σd1由73.07%增加为92.43%，这是由于攻击方由故障获得的额外收益减少，则需提高其继续攻击的概率以增加其收益值。防御方减少选择动态修复策略的概率为63.51%，使得故障持续率降低、攻击方继续攻击率增加的情况下防御方具有最佳收益值。当故障持续概率继续降低为50%，30%时，攻击方只有将继续攻击的概率提高至100%，才能保证其收益值最佳，此时防御方也只有以100%的概率选取动态修复策略时得到最佳收益值。

表2 纳什均衡仿真结果

3.2 多个攻击对象的模型建立分析

由于考虑了多个攻击对象，模型的复杂度将远远超过单个攻击对象时的模型复杂度，简化攻防策略，省略相似的攻防过程得到三方动态博弈模型如图8所示。

当攻击者的攻击对象为多个网络设备时，攻击者在发起攻击时没有确定攻击对象，那么在建立三方动态博弈模型时攻击者的攻击初始策略包含两个方面的内容，分别为攻击哪一个对象以及以什么方式攻击，以图3所示攻防模型为例，攻击者可选的攻击对象为节点n1、n2以及n3，可选的攻击方式有DoS攻击以及木马攻击。

三方动态博弈模型的建立是纳什均衡求解最基础也是最关键的部分，在给出完整的模型后，根据第2节中描述的粒子群算法求解纳什均衡，仅以n1故障情况下的博弈模型为例进行说明，仿真参数为：c1=c2=1，ωmax=0.9，ωmin=0.6，m=40，迭代 100 次得到纳什均衡结果如下

该纳什均衡结果与真实的纳什均衡结果的近似程度为99.99%，攻防双方按照该纳什均衡的结果选取策略将会得到最佳的收益。

4 结论

针对网络攻防对抗中生存防御策略的优化配置问题，提出了一种混合策略模式下基于三方动态博弈的网络攻防对抗模型。将提出的模型应用到一个网络实例中，对其策略选择过程进行分析，分别建立了单个攻击对象和多个攻击对象情况下的三方动态博弈模型，将两种情况下仿真得到的纳什均衡结果与实际的纳什均衡结果进行对比分析，均验证了所提理论的有效性和实用性。

［1］李黎，郑庆华，管晓宏.基于有限资源提升网络可生存性的拓扑重构方法［J］.物理学报，2014，63（17）：1-11.

［2］LIN Y S，CHEN P Y，CHEN Q T.Resource allocation strategies to maximize network survivability considering of average DOD［C］//Proc of 9th International Conference on Distributed Computing and Artificial Intelligence.Berlin：Springer Berlin Heidelberg，2012：751-758.

［3］林旺群，王慧，刘家红，等.基于非合作动态博弈的网络安全主动防御技术研究［J］.计算机研究与发展，2011，48（2）：306-316.

［4］ZHAO L R，MEI S E，ZHONG W J.Optimal configuration of firewall，IDS and vulnerability scan by game theory［J］.Journal of Southeast University（English Edition），2011，27（2）：144-147.

［5］伍文，孟相如，马志强，等.三方动态博弈网络可生存性策略选择［J］.应用科学学报，2014，25（4）：205-208.

［6］梁霄，孟相如，陈铎龙，等.基于随机博弈模型的网络可生存性跟踪评估［J］.火力与指挥控制，2013，38（9）：32-36.

［7］KAMHOUA C A，KWIAT K A，PARK J S.Surviving in cyberspace：a game theoretic approach［J］.Journal of Communications，2012，7（6）：436-450.

［8］FRIHAUF P，KRSTIC M，BASAR T.Nash equilibrium seeking in noncooperative games［J］.IEEE Transaction on Automatic Control，2012，57（5）：1192-1207.

［9］伍文，孟相如，康巧燕，等.粒子群算法求解混合战略近似 纳 什 均 衡 ［J］. 计 算 机 应 用 研 究 ，2014，31（8）：2302-2329.

Strategy Optimizing Selection of Network Survivability Based on Three Players’Dynamic Game Model

WU Wen，YANG Fa-liang，ZHANG Zhao-zhong，LIU Chang-le
（Unit 93936 of PLA，Yinchuan 750025，China）

A strategy optimizing selection algorithm for network survivable defense based on complete information dynamic game theory is proposed.It is to improve the network survivability in attack and defense process as viewed from optimizing the strategy combination.A three players’dynamic game model is given，the players respectively are attacker，accident and defender.The main elements of dynamic game are explained.A new mixed strategy Nash equilibrium theory is brought forward on the basis of classical Nash equilibrium.The expression of Nash equilibrium is no longer a qualification but a result led to values，which brought the concept of approximation.At last，the given model and algorithm are applied to a real network，the experimental results show that the model and algorithm are feasible and effective.

network survivability，strategy selection，dynamic game，nash equilibrium，particle swarm algorithm

TP393

A

10.3969/j.issn.1002-0640.2017.11.39

1002-0640（2017）11-0181-05

2016-09-21

2016-11-25

伍 文（1985- ），女，陕西西安人，博士。研究方向：网络可生存性。