空投鱼雷发现概率的解析模型研究

郑 强， 杨日杰， 陈佳琪， 单志超

(海军航空工程学院，山东 烟台 264001)

空投鱼雷发现概率的解析模型研究

郑 强， 杨日杰， 陈佳琪， 单志超

(海军航空工程学院，山东 烟台 264001)

针对空投鱼雷作战使用的特点，详细分析了影响空投鱼雷发现概率的3个要素,即鱼雷搜索区域、鱼雷入水点散布和潜艇散布，以及各要素间的相互作用，进而使用概率论的方法分别构建了精确信息源和模糊信息源下空投鱼雷发现概率的解析模型。实验结果表明解析法的计算结果与模拟法的仿真结果有较好的一致性。

空投鱼雷； 发现概率； 解析模型； 散布误差

0 引言

航空反潜因其具有速度快、搜索范围广、机动灵活、作战效率高等优势和显著特点成为反潜的优势兵力[1]。航空反潜的主攻武器是空投鱼雷，其最大优势就是可以弥补鱼雷本身航程短和航速低的不足。因此，各国都加强了对空投鱼雷相关技术的研究。鱼雷发现概率是预估鱼雷作战效能的重要指标，它是鱼雷攻击占位、射击决策的基本依据之一[2]。目前，在空投鱼雷作战效能的相关研究中，大多采用模拟法(蒙特卡罗法)[3]计算鱼雷发现概率，但其存在计算量大、难以形成理论体系等问题。

鉴于此，为完善空投鱼雷作战效能的相关理论研究，本文在分析空投鱼雷发现概率影响因素的基础上，构造了不同信息源下空投鱼雷发现概率的解析模型，并与模拟法的仿真结果相比较来验证它的正确性。

1 发现概率的影响因素

载机收到来自探测平台的目标潜艇信息后，火控系统据此解算鱼雷的投放参数，鱼雷经空中弹道伞降入水。显然，空投鱼雷的入水点相对潜艇的距离和方位可以是任意值。因此，鱼雷的发现概率取决于鱼雷的搜索弹道和鱼雷入水点与目标潜艇的相对位置。故研究的重点为空投鱼雷的搜索范围、入水点散布误差和潜艇散布误差。由于自导鱼雷在垂直面的搜索宽度足以覆盖潜艇深度的误差，可认为鱼雷在垂直面的发现概率为1，故只分析水平面上的搜索与散布问题[4]。

1.1 空投鱼雷的搜索模型

考虑到空投鱼雷入水点与目标潜艇相对位置的随机性，假设鱼雷采用环形搜索。以空投鱼雷理论入水点为坐标原点O，以投雷方向为x轴正向建立直角坐标系，本文所有的研究皆建立在此坐标系上，如图1所示,可见鱼雷的搜索范围为以其旋回中心OT为圆心的圆。若鱼雷的自导作用距离为l，旋回半径为r，搜索扇面半角为α，则鱼雷搜索范围的半径RT可由余弦定理表示为

(1)

通常鱼雷自导作用距离l远大于其旋回半径r，故可忽略O点与OT点之间的偏离。因此，鱼雷的搜索区域可等效为以其入水点O为圆心，以RT为半径的圆，即

(2)

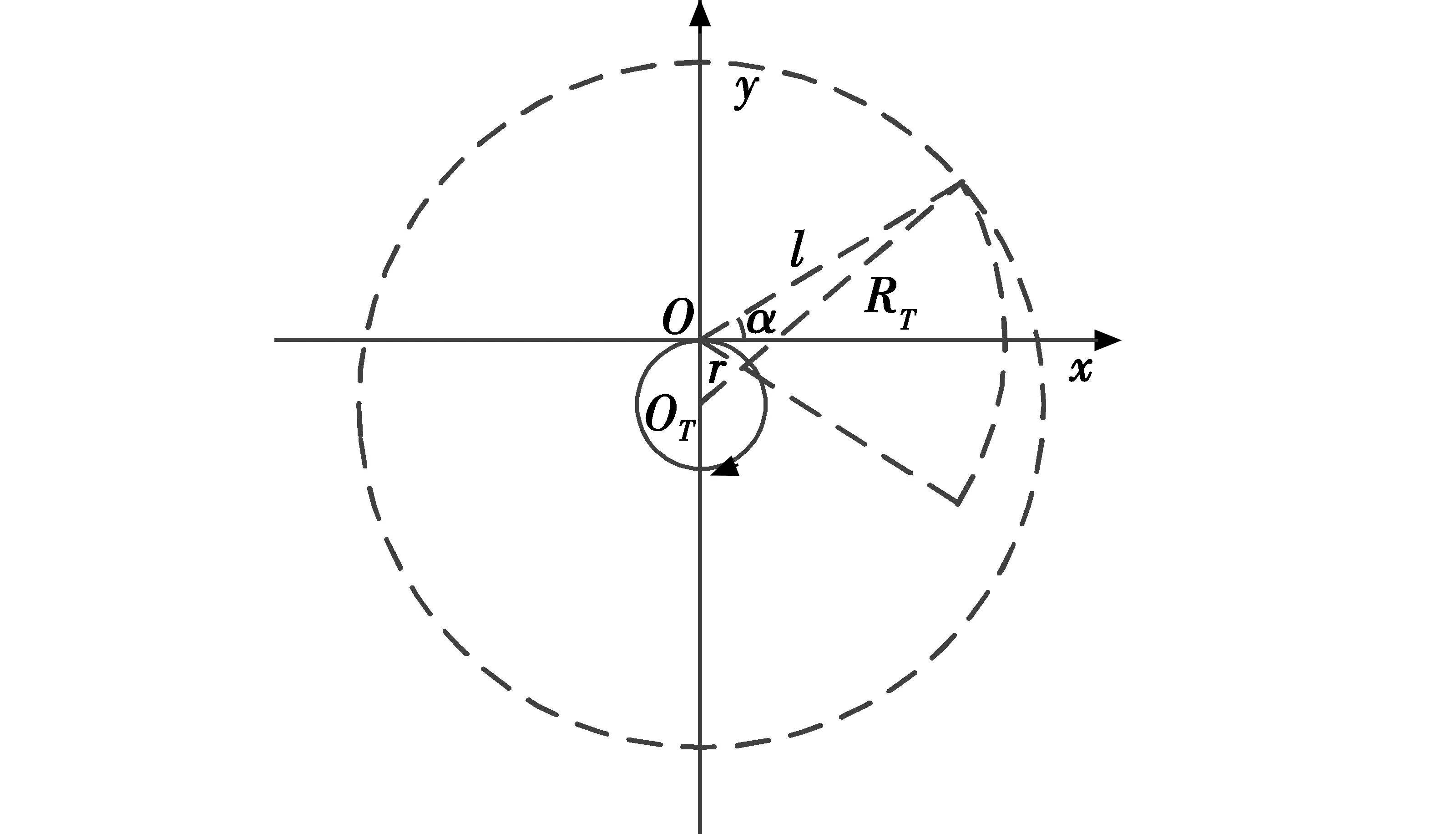
图1 空投鱼雷搜索区域示意图Fig.1 Searching area of airdrop torpedo

1.2 空投鱼雷入水点散布模型

鱼雷从投放到入水的整个过程中，影响其入水点位置的因素有很多，如火控系统误差、载机定位误差、空中弹道误差等，这些误差源共同决定了空投鱼雷的散布误差。已有研究表明，空投鱼雷的水平散布服从正态分布，且在鱼雷入水点的纵向和横向相互独立。设载机的飞行高度为H(单位:km)、飞行速度为V(单位：km/h)，依据飞行投雷散布的经验公式[5]，鱼雷在x方向和y方向的散布的均方差σxT，σyT可表示为

(3)

式中,ρ=0.476 9为常数。则空投鱼雷入水点散布的概率密度函数可表示为

(4)

1.3 潜艇散布模型

潜艇运动要素获取情况的不同，会导致潜艇散布模型的较大差异。因此，本文分别讨论精确信息源和模糊信息源两种情况下的潜艇散布问题。

1.3.1 精确信息源下的潜艇散布模型

(5)

式中：(x0,y0)为火控系统解算射击诸元时使用的潜艇当前点坐标；vS为潜艇的航速；β为潜艇的航向；时间t=ts+tf，其中,ts为系统的反应时间，可视为常量,tf=D/V为鱼雷的空中飞行时间，D为攻击距离，V为投雷速度。

实际情况下探测平台测得的潜艇位置、航速、航向信息必然包含了观测误差，则在空投鱼雷入水时潜艇的实际位置为

(6)

将上式进行三角变换后按一阶泰勒公式展开，然后忽略二阶小量并与式(5)相减可得

(7)

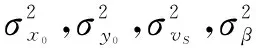
(8)

1.3.2 模糊信息源下的潜艇散布模型

模糊信息源下，在空投鱼雷前只知道潜艇当前的位置信息，航速、航向则难以获得，此时为了抢占攻敌的先机，通常瞄准潜艇当前位置点进行投雷。在该条件下，可认为从载机接收到目标潜艇信息直至鱼雷入水的整个时间t内，潜艇的航速和航向在0～vSmax和0～2π内均匀分布，其中,vSmax为潜艇最大航速。则潜艇在半径为vSmax×t的散布圆内均匀分布，圆心即为潜艇散布的中心，也是空投鱼雷的理论入水点。此时潜艇散布的概率密度函数为

(9)

2 空投鱼雷发现概率解析模型

针对上述不同信息源下的潜艇散布模型，构建其对应的发现概率解析模型。

2.1 精确信息源下的发现概率解析模型

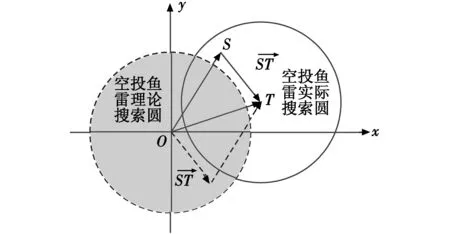
图2 精确信息源下的发现条件Fig.2 Detection condition based on accurate information source

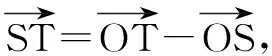
(10)

(11)

detC为C的行列式，C-1为C的逆矩阵。

综上所述，精确信息源下空投鱼雷发现概率的解析模型为

(12)

2.2 模糊信息源下的发现概率解析模型

模糊信息源下，由于鱼雷入水点散布服从二维正态分布，而潜艇散布服从均匀分布，故采用连续型全概率公式[7]，则空投鱼雷的发现概率可表示为

(13)

(14)

图3 模糊信息源下的发现区域Fig.3 Detection area based on fuzzy information source

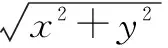
S=S(R)=

(15)

(16)

3 仿真分析

通过将解析计算结果与模拟仿真结果进行对比，来验证本文所构建的空投鱼雷发现概率解析模型的正确性。模拟法中入水点坐标根据其散布模型随机产生，鱼雷的水下运动模型、目标检测模型等均引自文献[8]。

设空投鱼雷的自导作用距离为1500 m、旋回半径为65 m、自导扇面半角为45°，投雷高度为100 m，投雷速度为150 km/h，ts=20 s，vSmax=24 kn(1 kn=1.852 km/h),每一条件下重复实验1000次。

3.1 精确信息源下仿真结果分析

实验中取vS=12 kn，β=90°，并由经验取σvS=3 kn,σβ=3°，则同过数值积分可求得解析法下的发现概率。模拟仿真中，潜艇的航速、航向要在vS,β的基础上加上随机观测误差。同理，潜艇的初始位置也要在(x0,y0)的基础上加上随机观测误差。

解析计算结果与模拟仿真结果如图4所示，可见，精确信息源下两者的偏差在5%以内，一致性较好，从而验证了精确信息源下发现概率解析模型的正确性。

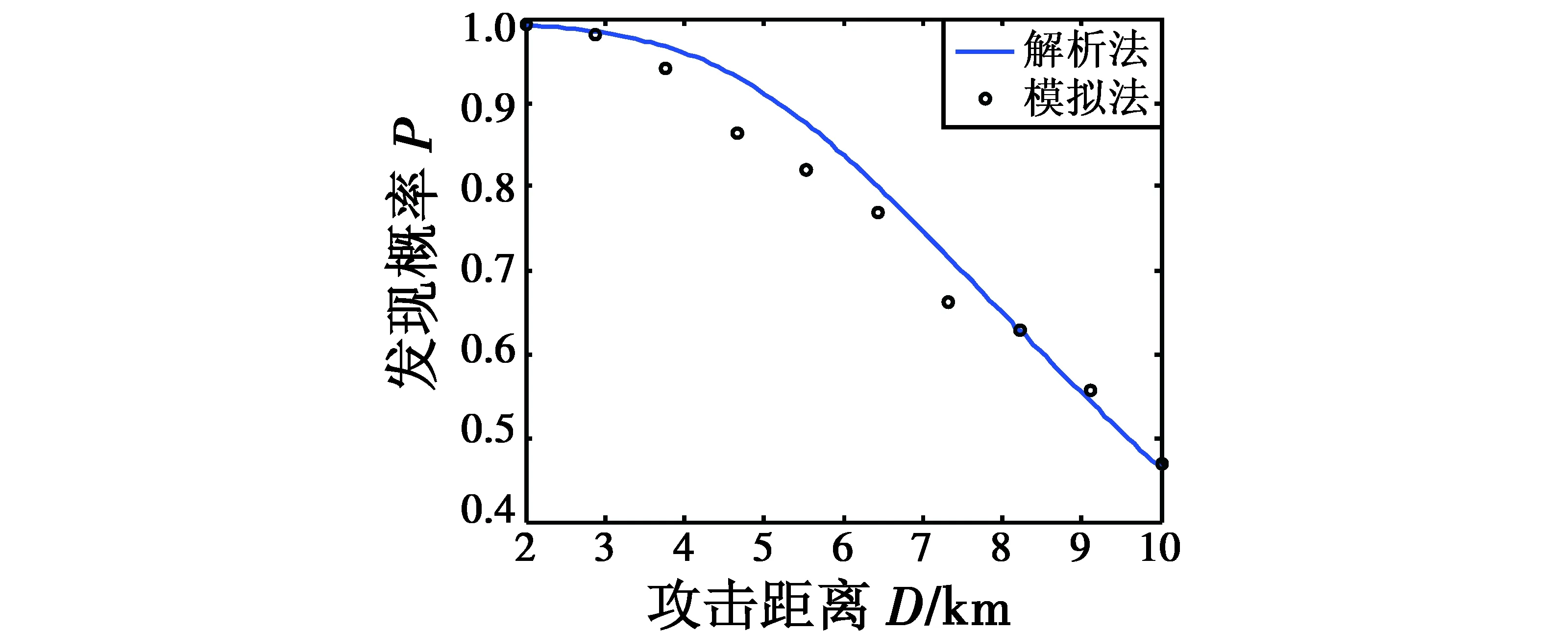
图4 精确信息源下攻击距离与发现概率的关系Fig.4 Attack distance vs detection probability based on accurate information source

3.2 模糊信息源下仿真结果分析

结合图4、图5可知，空投鱼雷的发现概率随着攻击距离的增大而减小，攻击距离相同时，精确信息源下的发现概率大于模糊信息源下的发现概率，且攻击距离越远优势就越明显。

图5 模糊信息源下攻击距离与发现概率的关系Fig.5 Attack distance vs detection probability based on fuzzy information source

此外，还可以看出，在攻击距离为4～8 km时，解析法的计算结果要略大于模拟法的仿真结果，而在2～4 km和8～10 km时，两者则较为接近,推测是因为解析法中未考虑鱼雷水下运动散布。近距离时，发现概率较大，鱼雷水下运动散布的影响有限；远距离时，空投鱼雷飞行时间较长，鱼雷水下运动散布相较其入水点散布来说影响较小。

4 结束语

本文就影响空投鱼雷发现概率的3个要素，即鱼雷搜索区域、空投鱼雷入水点散布和潜艇散布进行了分析，在此基础上构建了精确信息源和模糊信息源下的发现概率解析模型。解析法的计算结果与模拟法的仿真结果一致性较好，从而验证了所建解析模型的正确性。该解析模型可快速高效地给出各种态势下空投鱼雷发现概率的精确值，为战场决策提供依据。此外，研究成果完善了空投鱼雷作战效能的相关理论研究。但本文尚未考虑潜艇规避和使用水声对抗器材等情况，在今后的工作中将进一步完善。

[1] 陈遵银,王乃庆.航空自导鱼雷搜攻潜过程分析[J].弹道学报,2000,12(2):69-73.

[2] 孟庆玉,张静远,宋保维.鱼雷作战效能分析[M].北京:国防工业出版社,2003:165-169.

[3] 邵伟.蒙特卡洛方法及在一些统计模型中的应用[D].济南:山东大学,2012.

[4] 田恒斗,曹庆刚,侯代文,等.火箭助飞鱼雷捕获概率的解析模型[J].兵工学报,2013,34(7):916-921.

[5] 李居伟,赵志允,孙明太.反潜巡逻机空投鱼雷最佳投雷参数研究[J].鱼雷技术,2011,19(6):473-478.

[6] 盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008.

[7] 殷凤,王鹏飞.全概率公式的推广[J].数学的实践与认识,2014,44(11):313-316.

[8] 宫旭,蔡云祥.航空鱼雷最优落水点分析[J].指挥控制与仿真,2009,31(2):48-50.

OnAnalyticalModelofAirdropTorpedo’sDetectionProbability

ZHENG Qiang, YANG Ri-jie, CHEN Jia-qi, SHAN Zhi-chao

(Naval Aeronautical and Astronautical University,Yantai 264001,China)

According to the operation characteristics of the airdrop torpedo,three factors that have great effects on detection probability of the airdrop torpedo are studied in detail,including torpedo searching area,entry point dispersion and submarine dispersion.The interactions among the factors are also analyzed.Probability theory is used for constructing the analytical models of the detection probability respectively under accurate information source and fuzzy information source.The experimental results show that the calculation result of the analytical method is highly consistent with the result of the simulation method.

airdrop torpedo; detection probability; analytical model; dispersion error

TJ630

A

1671-637X(2017)03-0016-04

2016-09-29

2016-10-17

国家自然科学基金(61271444)

郑 强(1987 —),男，山东潍坊人，博士生，研究方向为航空反潜技术。