独立分量分析在重磁数据处理中的应用

马 龙 孟军海 付 强 山中雪 李宝兰

(①青海省第三地质矿产勘查院，青海西宁 810029； ②中国科学院青藏高原研究所大陆碰撞与高原隆升重点实验室，北京 100101； ③青海省第一地质矿产勘查院，青海平安 810600)

·非地震·

独立分量分析在重磁数据处理中的应用

马 龙*①孟军海①付 强②山中雪③李宝兰①

(①青海省第三地质矿产勘查院，青海西宁 810029； ②中国科学院青藏高原研究所大陆碰撞与高原隆升重点实验室，北京 100101； ③青海省第一地质矿产勘查院，青海平安 810600)

独立分量分析(ICA)能够通过发掘和去除数据间的高阶相关成分,使输出分量之间相互独立，对独立源信号进行分离和提取，是盲源分离(BSS)的核心技术。首先介绍了ICA的基本理论，运用基于负熵最大的FastICA(固定点算法)对算法原理进行说明和处理实验；然后根据重磁信号的特点对独立分量分析的应用进行初步探索，并用幂次方迭代的ICA算法进行了重力异常仿真实验，验证了方法在重力异常的分离和弱异常提取中的有效性；最后应用于实际磁测资料处理，有效识别了不同异常体。

独立分量分析 盲信号分离 位场分离 弱异常提取

1 引言

独立分量分析是近年逐步发展起来的一种新的信号处理技术，目的是从多维混合观测数据中分离出源信号[1,2]。它从多维观测数据的高阶统计特性出发，在对源信号(观测数据)及其混合矩阵(传输通道)未知的情况下，将多维观测数据按照统计独立的原则建立目标函数，通过ICA算法提取其中感兴趣的独立成分。ICA主要研究盲信号的分离问题，在语音分离、图像处理、生物医学和微阵列数据分析等方面应用广泛，而且在雷达探测、机械工程学、金融数据分析、生物信息等方面有较高的应用价值[3,4]。

地球物理勘探通过对观测数据信号求解未知场源体，属于反演问题[5,6]，而盲信号分离技术也是用观测数据求解源信号甚至信号的传输系统[7,8]，所以地球物理勘探中的部分问题属于盲信号分离理论的应用范围，用盲信号分离技术解决地理物理勘探中的某些问题在理论上是可行的。目前，ICA主要应用于地震勘探信号处理，特别是在地震资料去噪[9-14]、多次波压制[15,16]、目标地震信号的分解识别等方面取得了显著的应用效果[17]。

重磁勘探中所测得的重磁信号是地下多个地质体响应的线性混叠，属于线性瞬时混合信号。对这样的观测信号，传统的处理方式是区域异常和局部异常分离的二分法，方法有趋势分析法、滑动平均法、低通滤波法和匹配滤波等。这些方法分离出的“区域场”在数学意义上是多项式或不同频率成分的拟合，但是其地质和地球物理意义是模糊的，所以剩余(局部)场的概念也是相对的。小波变换引入了多尺度分析的思想，把位场异常分解成不同尺度的成分，结合其他方法和地球物理理论可给出相应的地质意义，它没有向上延拓的模糊性，使异常特征更清晰，信息更丰富。“磁亮点”识别的高阶统计量方法与宽度幅值特征滤波法在弱异常提取、不同尺度干扰的滤除方面应用效果良好[18-20]。

线性和非线性混合信号的盲分离方法主要有两大类：基于信息理论准则的迭代估计方法和基于信号高阶统计特性的代数方法，实质上两者都是利用了源信号的独立性和非高斯性。其中基于信息论准则的方法主要有：ICA算法、信息传输最大化(Infomax)算法、最小互信息(MMI)算法、最大似然估计(MLE)算法、负熵最大化算法；基于统计学的方法主要有二阶累积量、四阶累积量等高阶累积量方法。近几年出现的FastICA算法是基于定点递推算法得到的，能够适用于任何类型的数据，使ICA分析高维数据成为可能。本文选择基于负熵最大的FastICA方法说明ICA算法的原理，然后用幂次方迭代的ICA算法进行重力模型正演异常的分离和提取试验，最后将方法应用于磁测资料的处理。

2 ICA基本原理及算法

2.1 ICA基本原理

2.1.1 ICA模型

简单来说，ICA是根据多维数据x(t)的多阶统计量，寻找一组线性非正交坐标系，通过这个坐标系的投影变换，最终获取多维观测数据在统计意义上满足统计独立关系的另外一组数据s(t)的方法。以数学模拟信号为例，经过预处理的信号混合问题矩阵表达式为x(t)=As(t)，即

(1)

其反演问题可表述为

(2)

式中：t为样本引导值；x(t) =[x1，x2,…,xm]T为实际观测到的m维数据向量；s(t)=[s1，s2,…,sn]T为n维源信号向量;A为m×n维混合矩阵。在A和s(t)未知的情况下，独立分量分析要计算分离矩阵B(t)，分离后的信号y(t)相互最大程度独立。

在加噪声的条件下，线性混合信号表示为

x(t)=As(t)+N(t)

(3)

式中N(t)为噪声。

为了模型的可识别性，在上述描述中给定限制条件：

(1)源信号s(t)之间相互统计独立，且最多包含一个高斯分布的信号；

(2)观测的混合向量个数m不少于独立信号源的个数n，即m≥n，目的是简化问题。

目标源信号在从产生到被观测到的过程中经过相互的混叠和各种附加信号的影响，若要从观测到的多维观测数据中得到原始独立信号的有用信息，就要在只知道混合信号而不清楚源信号的先验知识和混合系统的条件下分离原信号。先验知识和混合系统的未知性就是盲信号分离(BBS)中的“两盲”。

图1 ICA处理系统示意图[21]

2.1.2 非高斯性的度量

Hyvarinen[22]指出ICA问题中信号的非高斯性就是独立性。盲信号分离中经典的非高斯性度量参数是峭度K(四阶累计量)，K(u)=E(u4)-3E2(u2),其中E(·)表示期望值。K=0表示信号u为高斯分布；K>0表示超高斯分布；K<0为亚高斯分布。K的绝对值越大，非高斯性越强[23-25]。

对于信号的概率密度函数p(u)(图2)，超高斯分布的显著特征是p(u)值在u的均值附近比其他区域值明显更大；亚高斯分布的p(u)曲线形态较为平缓，均值附近的p(u)值相对高斯分布要小，但是分布范围明显要宽。

实际工作中得到的重磁异常是由多个地质体重磁异常与外界各种噪声的叠加，带有随机性，所以要讨论其非高斯性。对于单个球体(球半径R=60m，球中心埋深D=100m，与围岩的密度差Δρ=1.0g/cm3)的重力异常，取球体正上方不同接收距离d处的正演信号计算其峭度(图3)，可以看出，在d=0～500m之间其峭度K>0。通过多种模型实验发现，重磁异常信号大多是非高斯信号，只有特定条件下的特定模型才是高斯信号，所以重磁信号满足源信号为非高斯性的条件，可对其进行独立分量分析。

图2 信号概率密度函数分布曲线

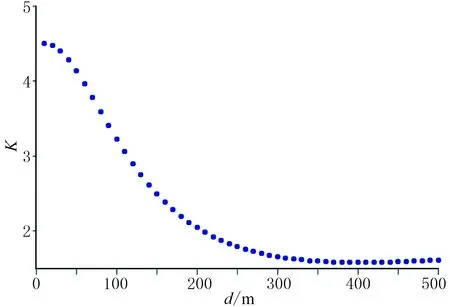
图3 重力信号的峭度随接收距离的变化曲线

2.2 算法原理

2.2.1 基于负熵的FastICA算法原理

基于负熵的FastICA算法是ICA算法中的一种，算法的固定点迭代是为了寻找负熵的近似值{E[g(Y)]-E[g(YGauss)]}2，g(·)为非线性函数，以此衡量非高斯性的最大值。根据信息论和中心极限定理可知：①在所有等方差的随机变量中，高斯变量的熵最大；②由相互独立的随机变量Si(i=1,2,3,…,N)之和组成的随机变量X较Si更接近高斯分布，因此在分离过程中，可通过分离信号的非高斯性来度量其相互独立性，当非高斯性度量达到最大时，表明已完成对各独立分量的分离。

负熵定义为

Gg(Y)=H(YGauss)-H(Y)

(4)

(5)

式中：YGauss是与Y具有相同方差的高斯随机变量；H(·)为随机变量的微分熵。根据相关的信息理论，高斯分布的随机变量具有最大的微分熵。当Y具有高斯分布时，Gg(Y)=0。Y的非高斯性越强，其微分熵越小，Gg(Y)值越大，所以Gg(Y)可以作为随机变量Y的非高斯性的度量。为了避免计算微分熵时需要计算Y的概率密度函数，采用如下近似公式

Gg(Y)={E[g(Y)]-E[g(YGauss)]}2

(6)

FastICA算法的规则是找一个方向使y=WTx具有最大的非高斯性，非高斯性用负熵Gg(WTx)的近似值来度量，WTx的方差约束为1。FastICA算法推导如下：首先，WTx的负熵的最大近似值可通过优化E[G(WTx)]获得；然后根据Kuhn-Tucker条件[26]， 在E[(WTx)2]=‖W‖2=1的约束下，E[G(WTx)]的最优值能在满足

E[xg(WTx)]+βW=0

(7)

JF(W)=E[xxTgT(WTx)]-βI

(8)

式中I为单位矩阵。由于数据白化性质E(xxT)=I，所以E[xxTgT(WTx)]≈E(xxT)·E[gT(WTx)]=E[gT(WTx)]I，因而雅可比矩阵变成了对角阵，并且较易求逆。最后得出近似的牛顿迭代法为

(9)

式中：W*是W的新值；β=E[WTxg(WTx)]。上式可简化为

W*=E[xg(WTx)]-E[gT(WTx)]W

(10)

此式即为基于负熵的FastICA迭代算法。

在实际工作中，理想情况下所有的有效数据都应该参与计算，但这会降低计算速度，所以通常用一部分样本的平均值来估计，样本数目的多少对最后估计的精确度有很大影响。迭代中的样本应该分别选取，假如收敛不理想的话可以增加样本数量。

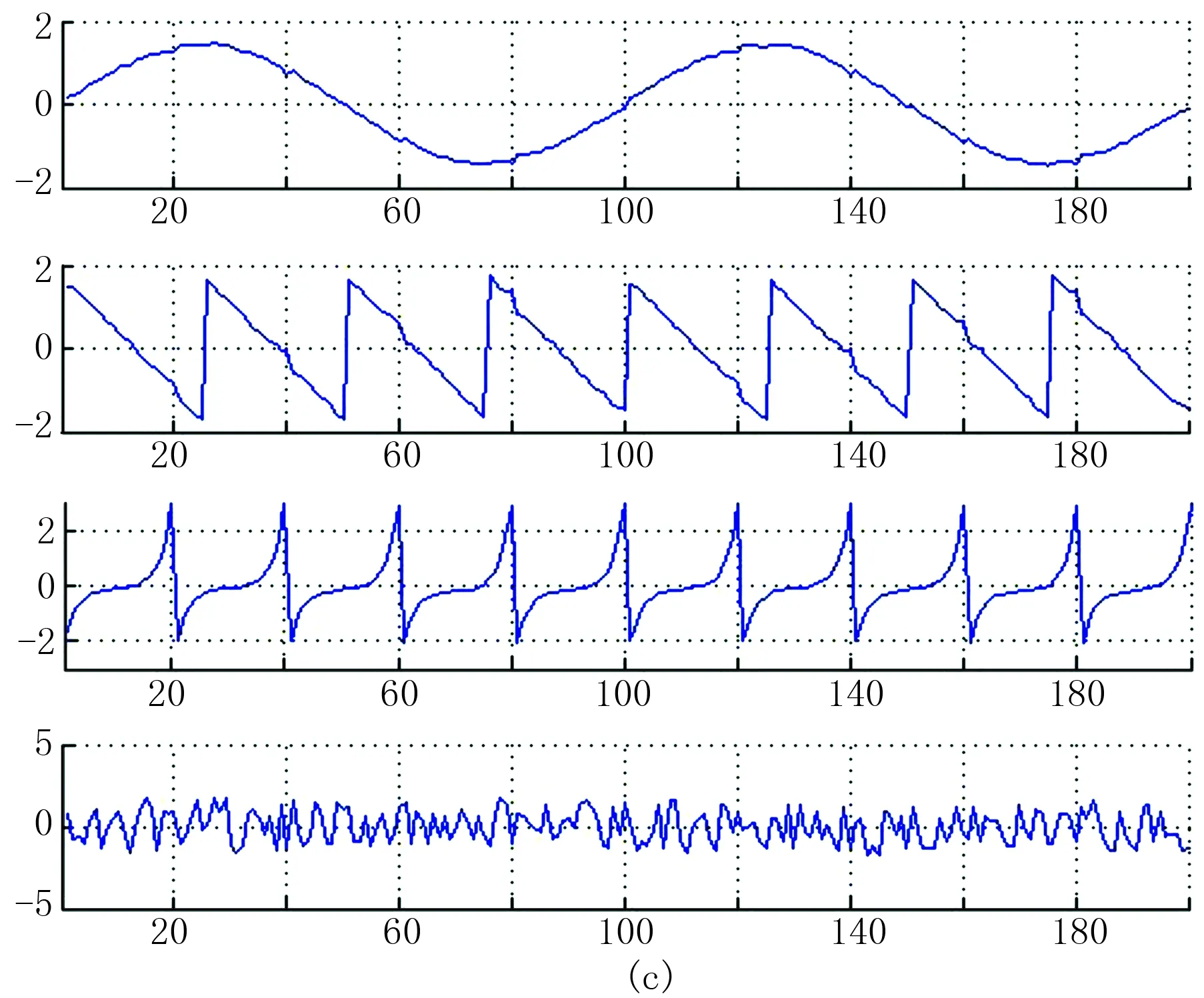
图4 利用FastICA算法进行数学信号分离实验结果

2.2.2 FastICA算法实验仿真

运用上述的FastICA算法进行数学信号分离实验，实验中源信号由matlab函数生成，分别是正弦信号、双曲正弦函数、锯齿信号和随机噪声。

图4为实验结果。从图4可以看出，执行ICA运算后，可以将图4a中的4种信号波形几乎完全分离出来，且误差较小。在周期性数学信号的形态分析中，个别信号的反相和幅值问题可以不予考虑，但在要求分析异常正负幅值的重磁信号中要做到两者均恢复。实验说明ICA分离算法可以有效分离出混叠信号中的独立分量信号。

3 模型实验

3.1 盲信号分离

盲信号分离是从多次观测信号中分离出目标信号，而重磁异常是多个地质体在观测面上的叠加，所以采用观测面上不同位置观测的信号代替多次观测信号。剖面实验中，采用不同间距两剖面上的正演数据作为待输入盲信号，平面实验中逐次取相邻两测线正演数据为待输入盲信号。

实验模型为一对球体，参数如表1所示，图5为组合体重力异常正演结果。其中测线方位角为0°，点距为10m，线距为10m。

表1 模型参数

图5 球体模型叠加重力异常正演平面图

下面对剖面数据进行ICA试算。考虑到算法的收敛速度及稳定性，采用幂次方迭代的独立分量方法进行信号处理。根据目标体的大小和数量选取合适的输入参数(测线数量和间距)，在此分别取两测线间距d为2R、2.6R和3.2R(R为球半径)的两条叠加重力异常进行处理(图5)。用误差能量Q[27]表示分离信号与源信号的相近程度。

图6～图8为ICA处理结果，可见分离出的信号中基本剔除了旁侧球体产生的信号影响，在横坐标为450～550m区域内两源信号交汇最严重(图5)，分离后1号球体产生的异常和2号球体产生的异常恢复到了与正演异常基本一致的形态， 局部细微的不吻合对于异常整体分析没有影响。总体来说，分离后异常信号的幅值和形态与单个球体的正演异常吻合较好。

图6 球体产生的重力异常正演和分离结果(d=2R)

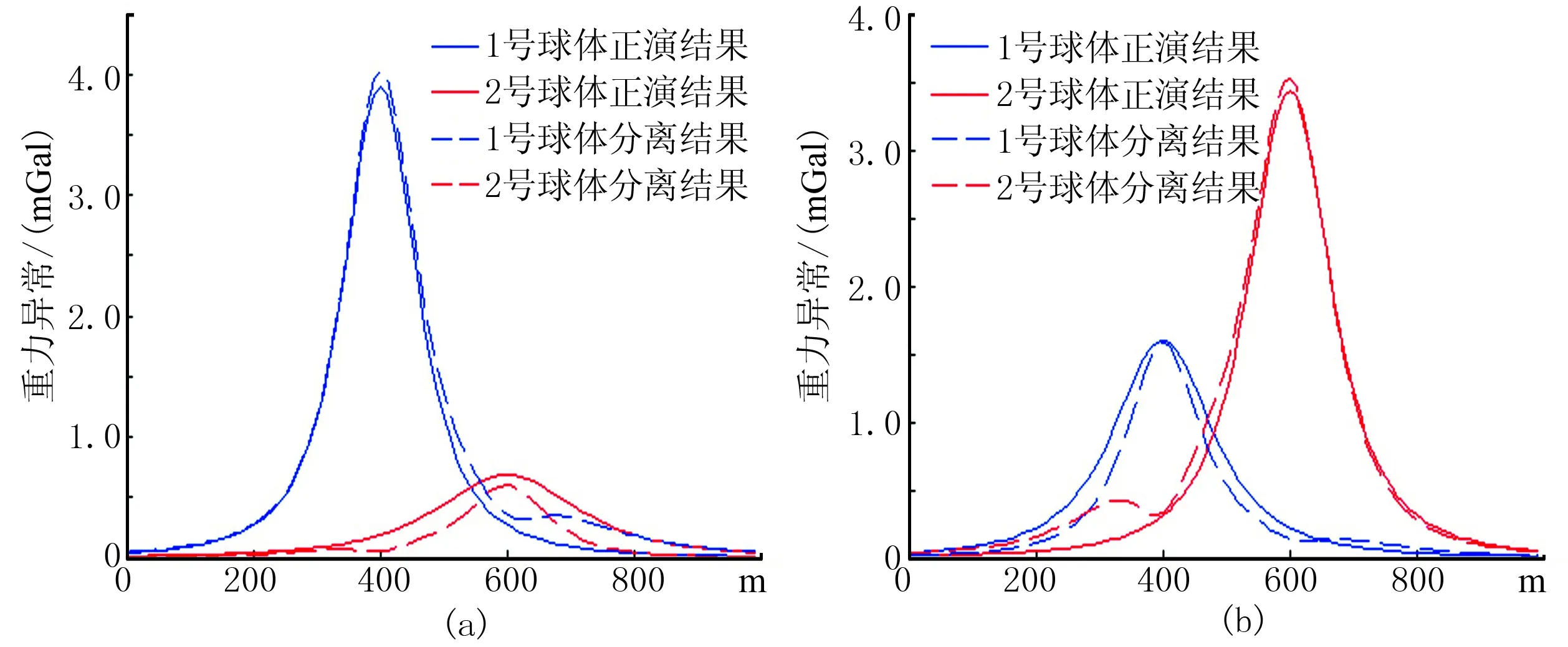
图7 球体产生的重力异常及分离结果(d=2.6R)

图8 球体产生的重力异常及分离结果(d=3.2R)

剖面位置球体1球体2剖面位置球体1球体2剖面位置球体1球体2430m0．01590．0160410m0．01490．0149400m0．01280．0128530m0．02230．0221540m0．01330．0134560m0．01170．0116

图9为滑动平均法的分离结果，可见虽然曲线的局部位置有两个对应的异常，但是幅值和形态都与图中源信号相差很大。剖面实验表明： 相对于传统位场分离方法(趋势分析、滑动平均等)，对于两个球体的混叠重力信号，FastICA迭代算法能够较好地实现观测信号分量的分离。

图10和图11分别为两个球体模型平面异常的正演和ICA分离结果。两个球体异常叠加后在球体正上方处的极值分别为5.69mGal和3.70mGal(图5)，ICA分离后其极值分别为5.43(图10右)和3.55(图11右)，比单独的正演极值5.45mGal(图10左)和3.49mGal(图11左)分别低0.02mGal和0.06mGal。可以看出分离得到的异常响应与正演响应在幅值和形态方面基本吻合，其中出现异常形态的“压扁”和局部微弱异常，可能是由于两信号之间在交错部位还有微弱影响，但不影响对两个球体的识别。总体来说实验效果比较理想，说明ICA法在重力数据处理中有较好的应用效果。

3.2 弱异常信息提取

为了验证ICA方法对弱异常信息的提取效果，用ICA算法从含有强背景场的混合重力异常信息中提取球体所产生的弱异常。背景场设为非线性背景场与随机噪声的组合，目标信号为球体产生的弱异常，其中弱异常峰值所占非线性背景场及随机噪声比例分别为4.63%和1.68%。球体模型3的参数：中心位置为(500m，500m，100m)，半径为50m，剩余密度为1.0g/cm3，测线方位角为0°(图12)。取纵坐标为500m和600m(相对于球体中心在地面投影点的偏移距离)两条测线的观测数据加上背景场为待输入盲信号(图13a)。

图9 滑动平均法重力异常分离结果

图10 1号球体的正演重力异常(左)和ICA分离结果(右)

图11 2号球体的正演重力异常(左)和ICA分离结果(右)

图12 3号球体产生的平面重力异常图 为了与图13中ICA分离结果进行对比，对混叠信号进行小波分解试验。利用小波变换对异常信号(500m剖面)进行分解、去噪处理。对比独立分量分析结果(图13b,图13c)与小波分析结果(图14)可以看出，ICA可以从强非线性背景场信号及噪声信号中提取弱异常信号，其分离结果与正演信号在幅值和形态方面吻合较好； 而小波各阶尺度分解结果都没有出现符合正演信号特征的独立信号。实验表明： 相对于小波分析位场分离方法等，ICA对弱异常信号的提取具有更好的应用效果。

图13 源叠加信号及ICA分离信号

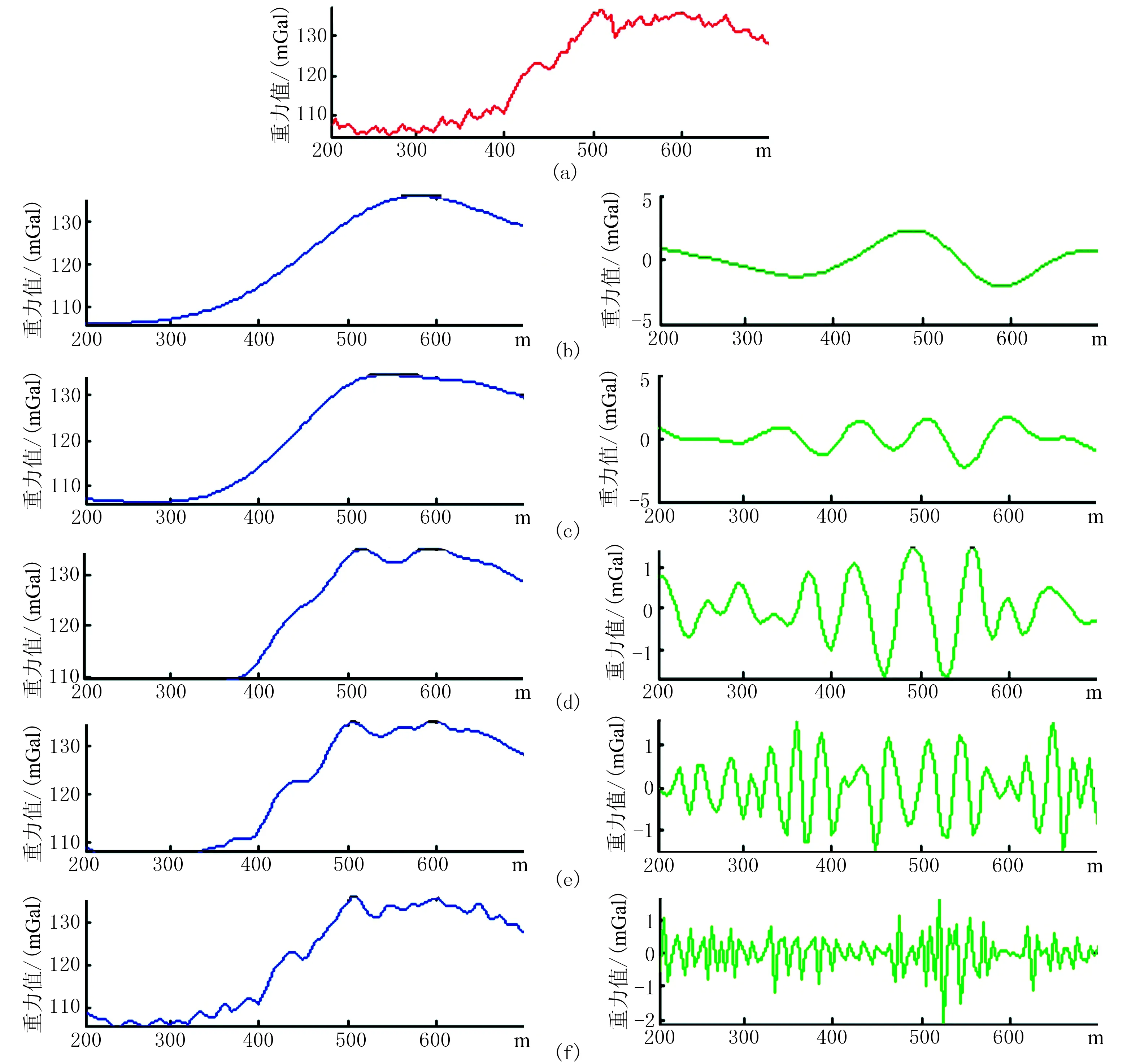
图14 源信号小波分解1～5阶逼近(左)和细节(右)

4 应用实例

为了验证方法的有效性，对某工区实测磁场资料进行ICA处理及解释。该项目的目的是通过分析岩体和磁铁矿体的磁异常特征，识别并解释磁铁矿体、寻找赋存的盲矿体。

矿区磁铁矿主要赋存于中—基性次生火山岩中，以辉绿岩为主。根据磁性参数统计可知：辉绿岩具有较强的磁性，C1类—C5类五个磁异常(图15a)都是磁铁矿和辉绿岩体共同产生的叠加异常，且以辉绿岩体引起的异常为主。可以将辉绿岩引起的异常看做区域异常，磁铁矿引起的异常作为局部异常，采用匹配滤波法来分离局部场和区域场，分离出的局部异常(图15b)是浅表岩石磁性增强及出露地表的磁铁矿体的反映。

为了突出已知矿体周围隐伏矿体和弱磁性(磁性较弱但块体较大)目标体异常，对磁异常ΔT进行ICA处理(图15d)。根据地质体走向和已知矿体大小等因素选取适当间距和数目的相邻测线作为输入信号，进行ICA处理。从结果可以看出在磁异常C1类以北的负异常区域出现一条明显的正异常带，带中心与已知的矿体在岩体中位置十分吻合。

根据平面异常特征，对0线异常剖面进行拟合(图16)和异常分离(图17)。剖面内有3个见矿钻孔：ZK002(见磁铁矿)、ZK004(见磁铁矿化体和磁铁矿)、ZK005(见三层磁铁矿化体和一层磁铁矿)(图18)。剖面磁异常包括钻孔所控制的矿体和矿化体的异常以及地层和岩体磁性的影响。解释时考虑到矿体、地层、岩体磁性的影响，结合地质剖面，建立已知矿体及围岩实际赋存模型(图18)，进行2.5维任意形状多边形截面模型的交互正反演，正演异常结果如图16所示。可以看出即使考虑地层产生的磁异常，仍有约1000nT左右的剩余磁异常欠拟合。

对0线ΔT异常进行ICA分离处理，结果见图17。可以看出分离出的局部信号中出现两个局部异常(虚椭圆)，极值达到1037nT，异常出现的位置基本对应图16中拟合异常欠值部位，异常的幅值也和图16中所欠幅值相近。推测这两个异常是目标盲矿体或矿化体引起的。

为了拟合正演曲线，根据地面磁测资料2.5维人机交互反演解释结果与钻探结果对剩余磁异常作进一步解释。将钻井控制的Fe3、Fe4矿化体沿产状向上延伸，进行综合交互反演。由图18可见，加入了磁化强度为20000×10-3A/m、磁化倾角为62°的地质体(图中白色矿体)后正演曲线基本拟合了实测磁异常曲线。这个磁参数符合实际钻遇矿体(矿化体)的磁参数(总磁化强度Ms为(10000～22000)×10-3A/m，总磁化倾角为62°)，所以模型中所加地质体为目标盲矿体具有充分的合理性。盲矿体异常与ICA方法提取的异常在幅值和位置方面对应很好，充分证明了ICA在重磁盲源体识别与弱异常提取中的实际应用效果。

图15 磁异常不同成分平面等值线图及剖面图

图16 0线围岩及矿体2.5维正演结果

图17 0线ICA分离局部磁力异常结果

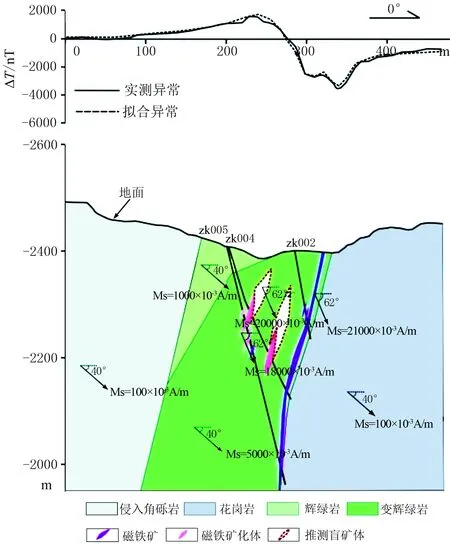
图18 0线地质模型(下)及2.5维精细反演(上)结果

5 结束语

(1)ICA方法能够从两球体混叠观测信号中分离和恢复出各自所产生的响应，分离效果理想，能在不受旁侧地质体及噪声信号影响的情况下精确地分析目标体所产生的信号，从而对目标信号赋予了明确的地球物理意义。

(2)由于地质构造的复杂性，基于“区域异常和局部异常”的数学模型较难做到混叠位场信号的独立分离；地球物理勘探能提供大量观测数据，但是对地下先验信息所知甚少，所以运用ICA方法提取重磁异常具有很好的应用前景。

(3)在实际磁测资料的处理中，ICA方法能够有效地提取目标弱缓成矿异常，当然，和别的地球物理方法一样，针对不同的情况需要选用合理的输入参数(输入信号数量和间距等)。

[1] 吴一全,曹照清,陶飞翔.基于Contourlet变换和ICA的多时相遥感图像变化检测.地球物理学报,2016,59(4):1284-1292.

Wu Yiquan,Cao Zhaoqing,Tao Feixiang.Change detection of multi-temporal remote sensing images based on Contourlet transform and ICA.Chinese Journal of Geophysics,2016,59 (4):1284-1292.

[2] 唐小亮,全海燕.基于遗传算法的重力固体潮信号独立元分析与地震前兆信息提取.地球物理学进展,2017,32(1):71-77.

Tang Xiaoliang,Quan Haiyan.Independent component analysis of gravity earth tide and extraction of seismic precursory signals based on genetic algorithm.Progress in Geophysics,2017,32(1):71-77.

[3] 孟小红,吴何珍,刘国峰.盲源反褶积方法与应用研究.石油地球物理勘探,2005，40(6):642-645，651.

Meng Xiaohong,Wu Hezhen,Liu Guofeng.Study of blind deconvolution and application of method.OGP,2005,40(6):642-645,651.

[4] Massoud B Z，Christian J.A general approach for mutual information minimization and its application to blind source separation.Signal Processing，2005，85(5):975-995.

[5] 撒利明,杨午阳,姚逢昌等.地震反演技术回顾与展望.石油地球物理勘探,2015,50(1):184-202.

Sa Liming,Yang Wuyang,Yao Fengchang et al.Past,present,and future of geophysical inversion.OGP,2015,50(1):184-202.

[6] 陈晓，于鹏，邓居智等.地球物理联合反演新框架研究.石油地球物理勘探，2017,52(4):851-858,883.

Chen Xiao,Yu Peng,Deng Juzhi et al.A new framework for geophysical joint inversion.OGP,2017,52(4):851-858,883.

[7] Chandra S，Throckmorton，Stacy L et al.Independent component analysis for UXO detection in highly cluttered environments.Journal of Applied Geophysics,2007,61(3-4):304-317.

[8] Mark E.Theoretical developments in electromagnetic induction geophysics with selected applications in the near surface.Surveys in Geophysics，2012，33(1):29-63.

[9] 刘喜武，刘洪，李幼铭.独立分量分析及其在地震信息处理中的应用初探.地球物理学进展，2003，18(1):90-96.

Liu Xiwu,Liu Hong,Li Youming.Independent component analysis and its testing application on seismic signal processing.Progress in Geophysics,2003,18(1):90-96

[10] 吕文彪，尹成，张白林等.利用独立分量分析方法消除地震噪声.石油地球物理勘探，2007，42(2):132-136.

Lü Wenbiao,Yin Cheng,Zhang Bailin et al.Using independent component analysis to eliminate seismic noises.OGP,2007,42(2):132-136.

[11] 魏巍.基于盲源分离的地震资料去噪技术.计算机仿真，2010，27(11):274-277.

[12] 张银雪,田学民.基于改进PSO-ICA的地震信号去噪方法.石油地球物理勘探,2012,47(1):56-62.

Zhang Yinxue,Tian Xuemin.Seismic de-noising based on the modified particle swarm optimization-independent component analysis.OGP,2012,47(1):56-62.

[13] 葸晓宇，刘洪，曾锐等.浅水型河流相的ICA地震识别方法.地球物理学进展，2006，21(3):856-863.

Xi Xiaoyu,Liu Hong,Zeng Rui et al.ICA seismic identification of shallow channel sedimentary subfacies.Progress in Geophysics,2006，21(3):856-863.

[14] 张艳丽，张守祥，王永强.基于独立分量分析方法的煤岩界面识别研究.信号处理，2007，23(4):85-87.

Zhang Yanli,Zhang Shouxiang,Wang Yongqiang.Identification of coal and rock interface based on independent component analysis.Signal Processing,2007,23(4):85-87.

[15] 刘天佑.位场勘探数据处理新方法.北京：科学出版社，2007.

[16] 刘天佑，崔宁，蔡鑫等.重磁异常宽度幅值特征滤波.石油地球物理勘探，1996，31(2):225-231.

Liu Tianyou,Cui Ning,Cai Xin et al.Characteristic filtering for the width and amplitude of gravimetric-magnetic anomaly.OGP,1996,31(2):225-231.

[17] 印兴耀,刘杰,杨培杰.一种基于负熵的Bussgang地震盲反褶积方法.石油地球物理勘探,2007,42(5):499-505.

Yin Xingyao,Liu Jie,Yang Peijie.A negative entropy-based Bussgang seismic blind de-convolution.OGP,2007,42(5):499-505.

[18] 李钟晓，陆文凯，庞廷华等.基于多道卷积信号盲分离的多次波自适应相减方法.地球物理学报，2012，55(4):1325-1334.

Li Zhongxiao,Lu Wenkai,Pang Tinghua et al.Adaptive multiple subtraction based on multi-traces convolutional signal blind separation.Chinese Journal of Geophysics,2012,55(4):1325-1334.

[19] 石颖，王建民，井洪亮等.多道自适应匹配滤波方法压制表面多次波.地球物理学进展，2013，28(2):785-792.

Shi Ying,Wang Jianmin,Jing Hongliang et al.Suppressing surface-related multiple by multi-trace adaptive matching filter approach.Progress in Geophysics,2013,28(2):785-792.

[20] 杨宇山,李媛媛,刘天佑.高阶统计量在地震弱信号及“磁亮点”识别中的应用.石油地球物理勘探,2005,40(1):103-107.

Yang Yushan,Li Yuanyuan,Liu Tianyou.Application of high-order statistics to identify weak seismic signal and “magnetic bright spot”.OGP,2005,40(1):103-107.

[21] Herbert B,Robert A,Walter K.TRINICON-based Blind System Identification with Application to Multiple-Source Localization and Separation:Blind Speech Se-paration.Springer,Netherlands,2007，101-147.

[22] Hynrinena O.Independent component analysis：algorithms and applications.Neural Networks，2000，13(4-5)：411-430.

[23] 卜涛.独立成分分析基本原理与发展.通信技术，2012，45(7):116-118.

[24] 石殿祥,李岩,殷福亮等.基于高阶累积量的非最小相位地震子波提取.石油地球物理勘探,1999,34(5):491-499.

Shi Dianxiang,Li Yan,Yin Fuliang et al.Non-minimum phase wavelet obtainment based on high-order accumulated amount.OGP,1999,34(5):491-499.

[25] 李舜酩，杨涛.盲源信号分离及其发展.传感器技术，2005，24(4):1-4.

Li Shunming,Yang Tao.Blind source separation and its development.Journal of Transducer Technology,2005,24(4):1-4.

[26] Harold W,Kuhn,Albert W.Nonlinear programming.Proceedings of 2nd Berkeley Symposium，1951,481-492.

[27] 刘天佑.相关滤波方法及其在扬子地台断裂分析中的应用.地质科技情报，1993，12(9):45-50.

*青海省西宁市城西区西川南路61号青海省第三地质矿产勘查院物探所，810029。Email:493316908@qq.com

本文于2017年3月27日收到，最终修改稿于同年10月8日收到。

本项研究受国土资源部公益性行业科研专项经费项目(201411025)和青海省科技厅重大科技专项(2016-SF-A3)联合资助。

1000-7210(2017)06-1344-10

马龙，孟军海，付强，山中雪，李宝兰.独立分量分析在重磁数据处理中的应用.石油地球物理勘探，2017,52(6):1344-1353.

P631

A

10.13810/j.cnki.issn.1000-7210.2017.06.026

(本文编辑：刘海樱)

马龙 硕士，1991年出生；2013年毕业于中国地质大学(武汉)应用地球物理专业，获学士学位；2015年毕业于中国地质大学(武汉)地质工程专业，获硕士学位；目前在青海省第三地质矿产勘查院从事地球物理数据处理、综合解释等方面的研究。