基于k最短路径的现代有轨电车线网优化
胡军红 过秀成 陶 涛 胡婷婷
(1东南大学交通学院, 南京 210096)(2南京工业大学交通运输工程学院, 南京 210009)
基于k最短路径的现代有轨电车线网优化
胡军红1,2过秀成1陶 涛1胡婷婷1
(1东南大学交通学院, 南京 210096)(2南京工业大学交通运输工程学院, 南京 210009)
为科学合理地进行现代有轨电车线网的优化与改进,基于现代有轨电车线网优化的约束条件,引入k最短路径算法进行线网优化.首先运用道路空间资源要素和线路重复系数这2个约束条件实现对初始网络图中有效边的筛选,形成备选线路集合,其次将非直线系数和节点综合重要度这2个约束条件组成联合熵权,将该联合熵权作为现代有轨电车最优路径的判定参数,从而构建满足多约束条件下的现代有轨电车线网优化方法.最后,以南京河西新城现代有轨电车线网优化为例,验证了该方法的有效性,表明k最短路径算法是适用于现代有轨电车线网规划的有效方法,该方法可为现代有轨电车线网规划提供参考.
现代有轨电车;k最短路径算法;联合熵权;线网优化
现代有轨电车线网规划是在城市综合交通体系规划、有轨电车交通功能定位和需求分析的基础上,构建初始线网,经优化与改进,形成最终方案的过程.目前线网生成常用方法包括“面、线、点”要素分析法、最优路径搜索法和逐线规划扩充法等.而k最短路径算法通过提供k条非递减的可供选择的最短路径备选方案集[1],在满足多种约束条件的情况下,可以使用户最大限度进行个性化选择,符合现代有轨电车线网优化的决策过程.
k最短路径是单一最短路径算法的改进与推广,在公共交通系统方面大多用于线网交通分配或公共交通路径选择与换乘研究.段宗涛等[2]提出了k最短路径集合算法,求交通网络中k个长度等级的最短路径集合,并将大规模交通网络下的交通流量分配至不同等级的最短路径,解决了交通流合理分配问题.徐涛等[3]提出约束Yen算法,运用于国际航线联程路径搜索问题.王莉等[4]认为针对公共交通系统用最短路径算法得到的往往不是最佳路径,通过引入最小换乘矩阵对待检验的标号进行筛选,可得到一条综合考虑换乘和路径长度的最佳路径.
本文拟在分析现代有轨电车线网优化约束条件的基础上,利用偏离路径算法构建k条最短路径备选方案集,采用联合熵权进行最优路径选择,实现初始线网优化的目标.然后以南京河西新城现代有轨电车线网优化为算例,进一步说明k最短路径算法在线网优化方面的应用.
1 现代有轨电车线网优化约束
现代有轨电车线网规划需要综合考虑不同交通方式之间的影响、区域重要集散点的分布、道路空间资源及实施条件等各方面制约关系.因此,线网规划是满足一定约束条件下的优化决策过程.在对初始线网进行优化改进时应考虑的主要约束条件包括:道路空间资源要素、线路重复系数、节点综合重要度、非直线系数等.
1) 道路空间资源要素是现代有轨电车线路敷设的基础条件,通常以道路用地边界线之间的道路红线宽度w作为关键要素,包括机动车、非机动车和行人交通所需的道路宽度.现代有轨电车系统一般选择城市主干路、次干路作为敷设线路的基础,要求道路红线宽度不少于30 m.
2) 线路重复系数β是指公共交通线路总长度与区域内线路网长度之比.公交线网重复系数以1.25~2.50为宜[5].为协调不同公共交通方式在线网层面的关系,提高城市公共交通系统整体运行效益,一般要求现代有轨电车线路不宜与城市快速轨道交通或快速公交(BRT)等城市骨干公交线路重复.在k最短路径算法中,线路重复系数β一般作为控制k条最短路径之间线路重复程度的约束条件.
3) 节点综合重要度主要依据线路中节点所在区域的区位条件、客流发生吸引的能力和集散点之间的相对交通可达性进行判断,一般采用熵值法或德菲尔法确定.现代有轨电车线网应尽可能覆盖城市主要客流集散点,为区域内主要节点提供快速高效的客流集散.规划区域内的集散点主要包括重要的集中居住区、商业中心、商务中心(CBD)、行政中心及各类学校、医院和文体活动场所.
4) 非直线系数ξ是表征线网中线路顺直性的指标.非直线系数定义为线路起讫间的实际线路距离与两点间空间直线距离的比值,公共交通线路非直线系数不应大于1.4,整个线网的平均非直线系数应以1.15~1.20为宜[6].现代有轨电车线路设置尽可能保持线型顺直,减少线网的换乘次数.
现代有轨电车线网优化是多约束条件下的决策过程,一般不存在全局最优解.而k最短路径算法能够在满足多约束条件的情况下,构建多重备选方案集来满足不同需求[7].
2 基于k最短路径的线网优化算法
2.1 问题描述
k最短路径问题是在网络图中以一种非递减的顺序寻找起点和终点间的多条备选优化路径,形成最短路径组,以最大程度满足用户对不同路径的选择需求.它除了要确定最短路径之外,还要确定第2短路径、第3短路径,直至找到第k条最短路径为止[8].
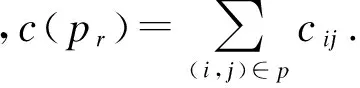
k最短路径问题是确定备选路径集合Pk={p1,p2,…,pk}∈Pst,并满足以下2个条件[9]:
① 备选路径集k条最短路径按非递减排序,即c(pr) ②k条最短路径任一条路径的权值均不大于s与t之间非备选路径的权值,即c(pk) k最短路径问题大致可分为限定无环问题和一般问题2种,现代有轨电车初始线网优化问题为限定无环k最短路径问题.计算过程是首先采用Dijkstra算法寻找第1条最短路径,然后采用偏离路径的概念计算第r+1(1≤r≤k-1)条最短路径,在求第r+1条最短路径时,将第r条路径上除了终止节点之外的所有节点都视为潜在的偏离节点进行计算,以偏离边的缩小长度最小作为寻找第k+1条最短路径的选择标准[10]. 该算法通过引入道路空间资源要素(如道路红线宽度w)对初始图G0=(V0,E0)中的边进行筛选,形成新的图G=(V,E);采用k最短路径算法计算第1条最短路径;引入线路重复系数β的概念,对偏离路径算法进行改进,计算第2至k条最短路径,形成备选路径集.重复计算网络图中的k最短路径,生成现代有轨电车线网备选方案集合.算法步骤如下: 1) 构建网络图.以城市规划道路网中的主干线和次干线作为边的集合V0,主要的线路节点及客流集散点作为节点的集合E0(重要的集中居住区、商业中心、商务中心(CBD)、行政中心及各类学校、医院和文体活动场所、交通枢纽场站等)构建初始网络图[11]. 2) 网络图筛选.根据现代有轨电车线网优化相关的约束条件,进行初始网络图筛选. ① 剔除不符合规划条件的边,如位于城市快速路上不宜敷设现代有轨电车线路的边,或者是与既有或规划的城市快速轨道交通线路重复达到一定限值的边. ② 引入道路红线宽度w不低于30 m这个约束条件,剔除不具备敷设现代有轨电车线路的边.对初始图G0=(V0,E0)中的边进行筛选优化后形成新的图G=(V,E). 3) 确定网络起终点组合集.选定起终点组合集OD=(S,T),(S=s1,s2,…,sN;T=t1,t2,…,tN).根据城市客流廊道和客流集散点空间分布确定的现代有轨电车初始线网,选定各线路通道需要连接的起始节点和终止节点OD组合数量.从而将现代有轨电车线网规划问题转变为确定起终点集OD=(S,T)中的每一组起始节点和终止节点(s1,t1),(s2,t2),…,(sN,tN)的k最短路径问题. 4) 求第1条最短路径p1. ① 以起始节点S作为当前节点i,权值赋值为ci=s=0,将当前节点保存到节点集合E′. ② 以路段长度作为边的权值,计算与当前节点i相邻的所有节点之间的权值cij,(i=S;j=1,2,…,h),h为与当前节点相邻的所有节点数量. ⑤ 重复执行步骤②~④,直到i=t时,算法结束,输出结果和权值cs.搜索到的最短路径信息为从s到t之间的最短路径节点集合E′,最短路径权值为cs;将其作为p1放入备选路径集合中. 5) 求最短路径pr+1. ① 选取偏离节点.取pr(1≤r≤k-1)中除了终止节点之外的每个节点vi作为可能的偏离节点. ③ 路径拼接.将从偏离节点vi至节点t之间最短路径与当前路径pr上从s至vi的路径拼接在一起,构成pr+1的一条路径候选路径,存入备选路径集合中. ④ 从候选路径列表中选择最短的一条路径作为pr+1,放入备选路径集合中. ⑤ 重复①~④,找到k条路径后,终止计算,并输出备选路径集合p=(p1,p1,…,pk),作为起始节点和终止节点之间的现代有轨电车线路的备选路径. 按照以上计算步骤,计算网络图中起终点集OD=(S,T)中的每一组起始节点和终止节点si,ti(i=2,…,N)的k条最短路径,生成现代有轨电车线网初始备选方案. 引入非直线系数ξ和节点综合重要度E(p)的联合熵权W(p)的概念作为选择现代有轨电车线路最优路径的参数.这样选出的线路路径不一定是最短路径,但一定是联合熵权最大的线路.逐一选择网络图中每一对起终点组合OD=(S,T)的现代有轨电车线路最优路径,从而实现对现代有轨电车初始线网的优化[12].计算步骤如下: ① 计算p=(p1,p2,…,pr,…,pk)中最短路径pr的非直线系数ξ(pr),且 (1) 式中,ξ(pr)为最短路径pr的非直线系数;d(s,t)为起终点(s,t)空间直线距离. ② 计算pk最短路径的节点综合重要度E(pr),且 (2) 式中,Ei为pr最短路径节点i的重要度.可以通过调查节点Ei的区位条件(节点所在区域、所在地段、周边主要用地性质)、客流发生与吸引能力(吸引范围内居住人口数、就业岗位数、商业零售数、客流分布方向的影响)、相对可达性(客流到达难易程度、周围路网等级级配)等进行综合确定. ③ 计算pr最短路径联合熵权W(pr),且 (3) 式中,W(pr)为pr最短路径的联合熵;α为权重系数. ④ 选择最优路径.从s到t之间的现代有轨电车线路中,选取联合熵权W(p)最大的最短路径作为最优路径,即 W(p)=max{W(p1),W(p2),…,W(pk)} (4) 按照以上计算步骤,对网络图中起终点集OD=(S,T)中的每一组起始节点和终止节点(si,ti)(i=2,3,…,N)的最优路径进行选择,实现对现代有轨电车初始线网方案的优化. 以南京河西新城为例,基于k最短路径算法构建现代有轨电车网络图,引入联合熵权进行线网优化,确定现代有轨电车线网布局方案. 4.1.1 构建网络图并选定起始点组合 基于河西地区的集散点分布,以河西地区主干路和次干路为主,构建初始网络图G0=(V0,E0),如图1所示.该初始网络图包含42个节点组成的V0集合和63条边组成的E0集合. 图1 南京河西新城现代有轨电车初始网络(单位:km) 根据南京河西新城道路空间资源条件对初始网络图中的边进行筛选,形成新的网络图G=(V,E),其中V为筛选后所有41个节点的集合,E为筛选后所有53条边的集合,采用连接道路长度给各边赋值,如图1所示.选定各线路通道需要连接的起始节点和终止节点OD组合,即OD={(s1,t1),(s2,t2),…,(s6,t6)}. 4.1.2 现代有轨电车线网备选方案集 按照前述初始线网生成模型与方法,计算网络图中每一组起始节点和终止节点si,ti(i=1,2,…,N)的k最短路径,生成现代有轨电车线网初始备选方案集. 以起终点s1,t1为例,设定k=3,β≤1.2.按前述寻求最短路径的计算步骤搜索现代有轨电车k最短线路: ① 第1条最短路径p1=(s1,3,6,10,15,t1),q1=(1.53,1.32,1.16,1.57,0.95),c(p1)=6.53 km. ② 第2条最短路径p2=(s1,1,s2,7,12,17,t1),q2=(0.49,1.52,0.94,1.21,1.98.1.75),c(p2)=7.89 km. ③ 第3条最短路径p3=(s1,2,s4,4,5,8,9,11,14,16,t1),q3=(0.41,1.41,1.41,0.91,0.63,0.71,0.82,0.99,0.94,0.96),c(p3)=9.19 km.找到给定的k=3条路径后,终止计算,并输出备选路径集合p=(p1,p2,p3),作为起始节点和终止节点s1,t1的备选路径. ④ 重复以上步骤,计算起始节点和终止节点si,ti(i=2,3,…,N)之间的备选路径组,生成现代有轨电车初始线网备选方案集. 从每一对起始节点和终止节点si,ti(i=2,3,…,N)之间的备选路径组中选择最优路径,实现对初始线网方案的优化.具体步骤如下: ① 根据c(p1)=6.53 km,c(p2)=7.89 km,c(p3)=9.19 km,d(S1,T1)=6.05 km,按式(1)计算p=(p1,p1,p3)中最短路径pr的非直线系数. ② 采用德菲尔法和式(2),计算最短路径pr的节点综合重要度E(pr),E(p1)=1.43,E(p2)=0.85,E(p3)=1.05. ③ 按照式(3),权重系数α取0.35,计算最短路径pr的联合熵权W(pr),W(p1)=1.25,W(p2)=0.82,W(p3)=0.91. ④ 选取联合熵最大的最短路径pr作为从s1到t1之间的现代有轨电车线路最优路径,即 W(p)=max{W(p1),W(p2),…,W(pk)}= max{1.25,0.82,0.91}=W(p1) 最优线路为p1=(s1,3,6,10,15,t1),线路长度c(p1)=6.53 km. 同理,选定其他现代有轨电车线路需要连接的起讫节点OD组合(s2,t2),(s3,t3),(s4,t4),(s5,t5),(s6,t6),进行k最短线路和最优线路选择. 原河西现代有轨电车规划线网是在点、线、面要素分析法的基础上生成,所推荐的线网由12条线路组成,线网规模约70.7 km.利用k最短路径算法优化后的河西现代有轨电车线网布局方案如图2所示,线网总规模约56.5 km,形成“四纵、四横、一联”的布局结构,从线网布局规划来看,线路走向与现状的实际客流方向一致,线网结构与河西新城布局形态相协调. 图2 河西新城现代有轨电车线网布局图(单位:km) 本文研究了现代有轨电车线网优化方法,在构建网络图的基础上,引入道路空间资源要素、线路重复系数的约束条件实现对初始网络图有效边的筛选.运用改进的偏离路径算法,生成k条最短路径,从而构成备选线路集合,引入节点综合重要度和非直线系数作为约束条件计算出联合熵权,选取联合熵权最大的线路作为最短线路,使线网优化决策过程最大限度契合线网功能需求、发展定位和实施条件,确定最终线网布局方案.并以南京河西新城为例进行应用研究,优化结果表明k最短路径算法是适用于线网规划的一种有效的优化方法. ) [1] 白轶多,胡鹏, 夏兰芳, 等.关于k次短路径问题的分析与求解[J].武汉大学学报(信息科学版), 2009, 34(4):492-494. Bai Yiduo, Hu Peng, Xia Lanfang, et. Akth-shortest path algorithm based onk-1 shortest paths[J].GeomaticsandInformationScienceofWuhanUniversity, 2009,34(4):492-494. (in Chinese) [2] 段宗涛, Wang Weixing, 康军, 等. 面向城市交通网络的k最短路径集合算法[J]. 交通运输系统工程与信息, 2014, 14(3): 194-200. DOI:10.3969/j.issn.1009-6744.2014.03.030. Duan Zongtao, Wang Weixing, Kang Jun, et al. Ak-th shortest path set algorithm for urban traffic network[J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2014,14(3): 194-200. DOI:10.3969/j.issn.1009-6744.2014.03.030.(in Chinese) [3] 徐涛, 丁晓璐, 李建伏. 国际航线网络联程路径搜索的KMCSP问题研究[J]. 西南交通大学学报, 2014, 49(1): 153-159. DOI:10.3969/j.issn.0258-2724.2014.01.024. Xu Tao, Ding Xiaolu, Li Jianfu.K-multiple constrained shortest paths problem for connecting path search in international flight path network[J].JournalofSouthwestJiaotongUniversity, 2014,49(1): 153-159. DOI:10.3969/j.issn.0258-2724.2014.01.024.(in Chinese) [4] 王莉, 李文权. 公共交通系统最佳路径算法[J]. 东南大学学报(自然科学版), 2004, 34(2): 264-267. DOI:10.3321/j.issn:1001-0505.2004.02.029. Wang Li, Li Wenquan. Best-routing algorithm for public transportation systems[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2004,34(2): 264-267. DOI:10.3321/j.issn:1001-0505.2004.02.029.(in Chinese) [5] 中国公路学会《交通工程手册》编委会.交通工程手册[M]. 北京:人民交通出版社,1998:234. [6] 中华人民共和国建设部.GB 50220—1995城市道路交通规划设计规范[S].北京:中国计划出版社,1995. [7] 郝光, 张殿业, 冯勋省. 多目标最短路径模型及算法[J]. 西南交通大学学报, 2007, 42(5): 641-646. DOI:10.3969/j.issn.0258-2724.2007.05.024. Hao Guang, Zhang Dianye, Feng Xunsheng. Model and algorithm for shortest path of multiple objectives[J].JournalofSouthwestJiaotongUniversity, 2007,42(5): 641-646. DOI:10.3969/j.issn.0258-2724.2007.05.024.(in Chinese) [8] Yen J Y. Finding theKshortest loopless paths in a network[J].ManagementScience, 1971,17(11): 712-716. DOI:10.1287/mnsc.17.11.712. [9] Androutsopoulos K N, Zografos K G. Solving the-shortest path problem with time windows in a time varying network[J].OperationsResearchLetters, 2008,36(6): 692-695. DOI:10.1016/j.orl.2008.07.003. [10] Wang Z P,Li G,Ren J W.A new search algorithm for transmission section based onkshortest paths[J].TransactionsofChinaElectrotechnicalSociety, 2012,27(4):193-201. [11] Gao Z Y, Zhao X M, Huang H J, et al. Research on problems related to complex networks and urban traffic systems[J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2006,6(3):41-47. [12] 马超群,王玉萍.基于客流效益最大化的轨道交通线网优化方法[J].长安大学学报(自然科学版),2010,30(1):76-79. Ma Chaoqun, Wang Yuping. Method to optimize urban rail transit network based on maximizing the passenger flow [J].JournalofChang’anUniversity(NaturalScienceEdition),2010,30(1):76-79. Optimizationofmoderntramnetworkbasedonk-shortestpathalgorithm Hu Junhong1,2Guo Xiucheng1Tao Tao1Hu Tingting1 (1School of Transportation, Southeast University, Nanjing 210096, China) In order to carry out the optimization and improvement of the modern tram network scientifically and rationally, thek-shortest path algorithm is introduced based on the constraint conditions of modern tram network optimization. Road space resource factors and path duplication factors are used to select the proper edges in the initial network and a set of alternative paths is formed. The non-linear coefficient and node comprehensive importance degree are combined into joint entropy weight, and the joint entropy weight is used as the judgment parameter of the optimal path of modern tram. Then, the modern optimization method for tram line is constructed. Finally, the effectiveness of the method is verified through the practical example of Nanjing Hexi new urban district modern tram network optimization. It is shown that thek-shortest path algorithm is an effective method for modern tram network planning. This method can provide a reference for urban tram network planning. modern tram;k-shortest path algorithm; joint entropy weight; network optimization 10.3969/j.issn.1001-0505.2017.06.030 U491.13 A 1001-0505(2017)06-1274-05 2017-05-06. 胡军红(1974—),女,博士生,副教授;过秀成(联系人),男,博士,教授,博士生导师,seuguo@163.com. 江苏省交通运输科技资助项目(2015Y17). 胡军红,过秀成,陶涛,等.基于k最短路径的现代有轨电车线网优化[J].东南大学学报(自然科学版),2017,47(6):1274-1278. 10.3969/j.issn.1001-0505.2017.06.030.2.2 k最短路径算法


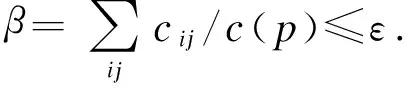
3 现代有轨电车初始线网优化
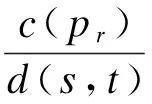
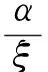
4 算例
4.1 南京河西新城现代有轨电车网络图
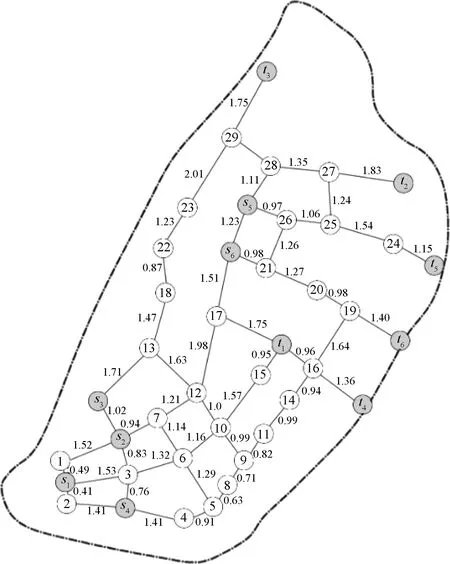
4.2 南京河西新城现代有轨电车线网优化
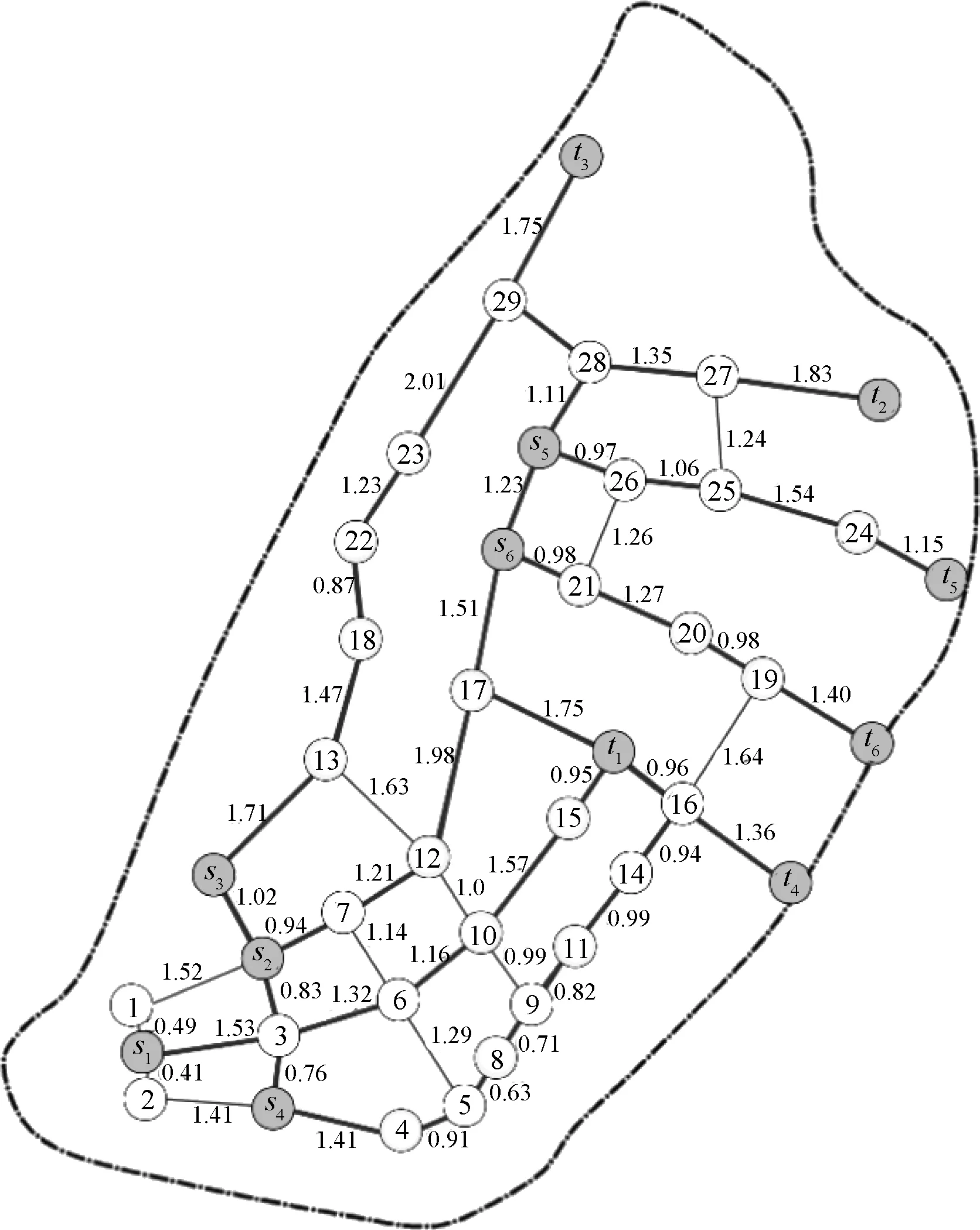
5 结语
(2College of Transportation Science and Technology, Nanjing Technology University, Nanjing 210009, China)

